Похожие презентации:
Начертательная геометрия. Пересечение плоскостей
1.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯПересечение плоскостей
Слайд-фильм
z
V
A"
y
A'''
W
A
x
z
o
x
A'
H
2013 г.
y
2.
312
3.5.1. Прямая линия, пересекающая плоскость
Поставлена задача:
Определить точку К пересечения данной прямой а с плоскостью a.
Определить видимость прямой.
Решение задачи выполняется в три этапа.
Алгоритм решения задачи
1
Заключить данную прямую во
вспомогательную плоскостьпосредник (проецирующую или
уровня)
3
2
Построить линию пересечения
вспомогательной плоскостипосредника с заданной
Найти точку пересечения
полученной линии пересечения с
заданной прямой
Символическая запись алгоритма
a S(S')
m=S a(ABC)
K=m a
Определить видимость прямой a по правилу конкурирующих точек
3.
32S
Геометрические образы (пл. АВС, прямая а)
спроецированы на плоскость П.
a
B
A
А теперь посмотрите как выполняются эти
этапы алгоритма на пространственном рисунке
и при проецировании всех элементов задачи на
плоскости П.
C
Выполняем 1-й этап алгоритма
B'
A'
H
C'
a S(S')
4.
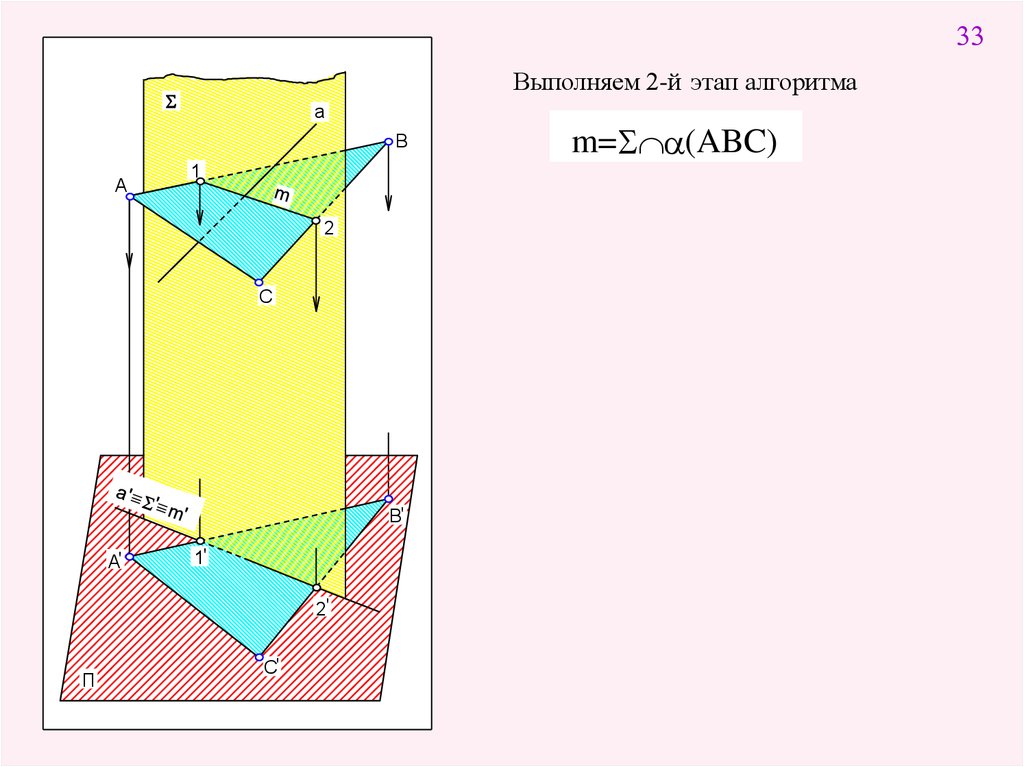
33Выполняем 2-й этап алгоритма
S
a
B
A
1
2
C
B'
A'
1'
2'
П
C'
m=S a(ABC)
5.
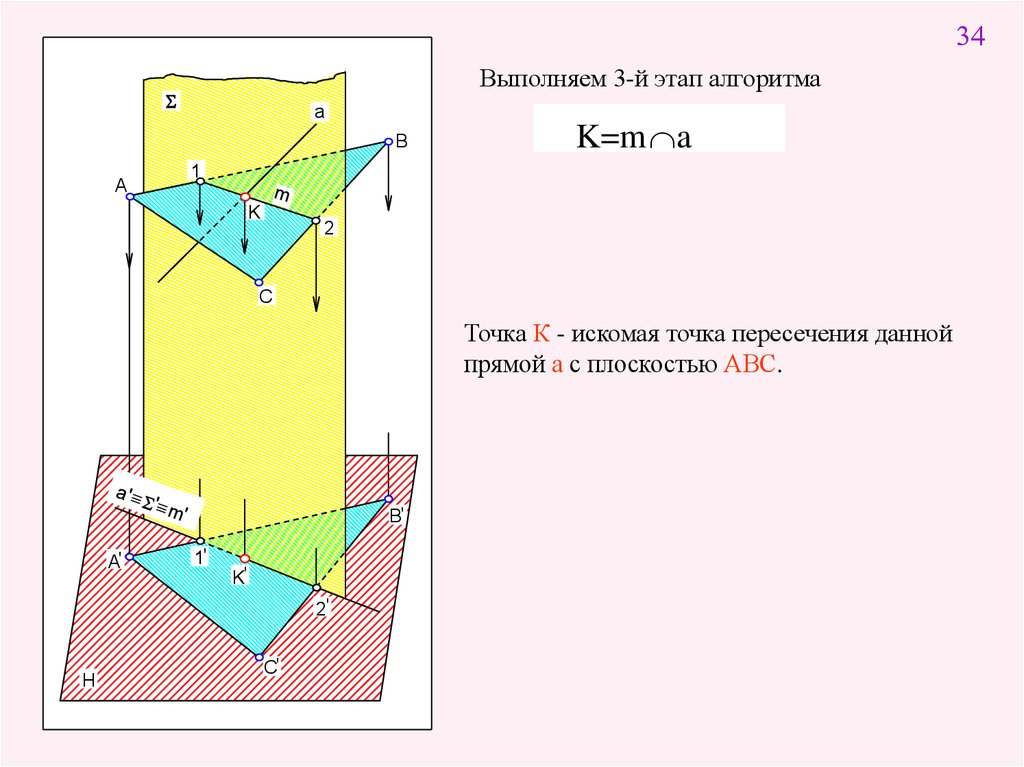
34Выполняем 3-й этап алгоритма
S
a
B
A
K=m a
1
K
2
C
Точка К - искомая точка пересечения данной
прямой а с плоскостью АВС.
B'
A'
1'
K'
2'
H
C'
6.
35Рассмотрим применение данного алгоритма при решении
задачи на построение точки К пересечения прямой а с
плоскостью a. Возможны три варианта условия данной
задачи:
- прямая а - общего положения, плоскость a проецирующая (или уровня);
- прямая а - проецирующая, плоскость a - общего
положения;
- прямая а - общего положения, плоскость a - общего
положения.
Решение первых двух задач можно выполнить, не применяя
алгоритма, так как один из заданных образов частного
положения.
7.
36C2
A2
K2
a2
B2
a1
C1
A1
K1
B1
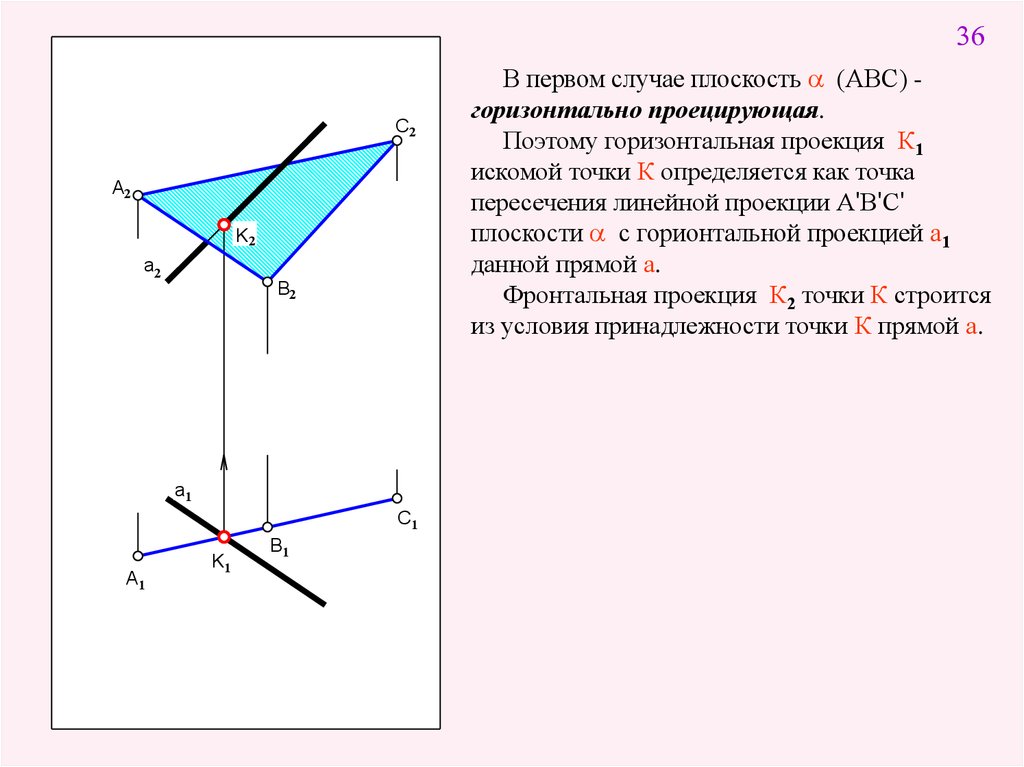
В первом случае плоскость a (АВС) горизонтально проецирующая.
Поэтому горизонтальная проекция К1
искомой точки К определяется как точка
пересечения линейной проекции А'В'С'
плоскости a с горионтальной проекцией а1
данной прямой а.
Фронтальная проекция К2 точки К строится
из условия принадлежности точки К прямой а.
8.
37B"
A"
_
a" _ K "
1"
Построение горизонтальной проекции К'
точки К выполняется из условия принадлежности точки К плоскости a: точка К
принадлежит плоскости a, так как она
принадлежит ее прямой A1 (К' находится как
точка пересечения прямой A' 1' с прямой а' ).
C"
B'
a'
A'
K'
1'
C'
Во втором случае прямая а - фронтальнопроецирующая.
Поэтому фронтальные проекции любой ее
точки, а также и искомой К пересечения а с
плоскостью a (АВС), совпадает с ее вырожденной проекцией a" К".
Видимость прямой а в этих задачах решается просто - с помощью реконструкции данных
образов (по наглядности).
9.
38a2
c2
d2
c1
d1
a1
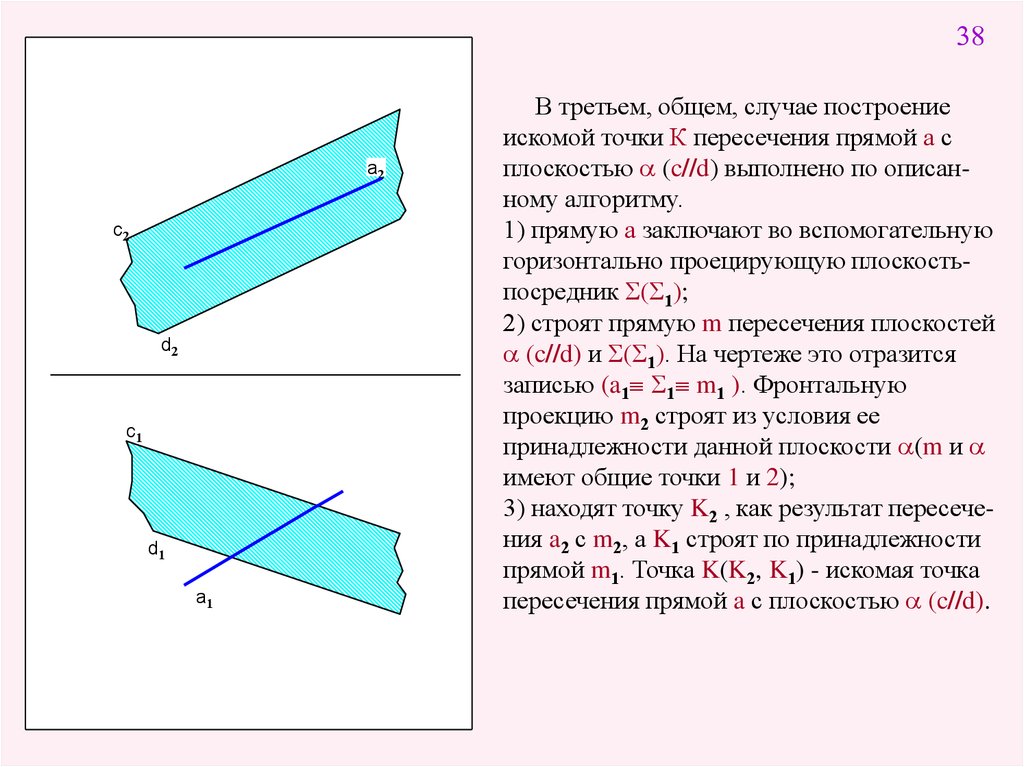
В третьем, общем, случае построение
искомой точки К пересечения прямой а с
плоскостью a (c//d) выполнено по описанному алгоритму.
1) прямую а заключают во вспомогательную
горизонтально проецирующую плоскостьпосредник S(S1);
2) строят прямую m пересечения плоскостей
a (c//d) и S(S1). На чертеже это отразится
записью (a1 S1 m1 ). Фронтальную
проекцию m2 строят из условия ее
принадлежности данной плоскости a(m и a
имеют общие точки 1 и 2);
3) находят точку K2 , как результат пересечения a2 с m2, а K1 строят по принадлежности
прямой m1. Точка K(K2, K1) - искомая точка
пересечения прямой a с плоскостью a (c//d).
10.
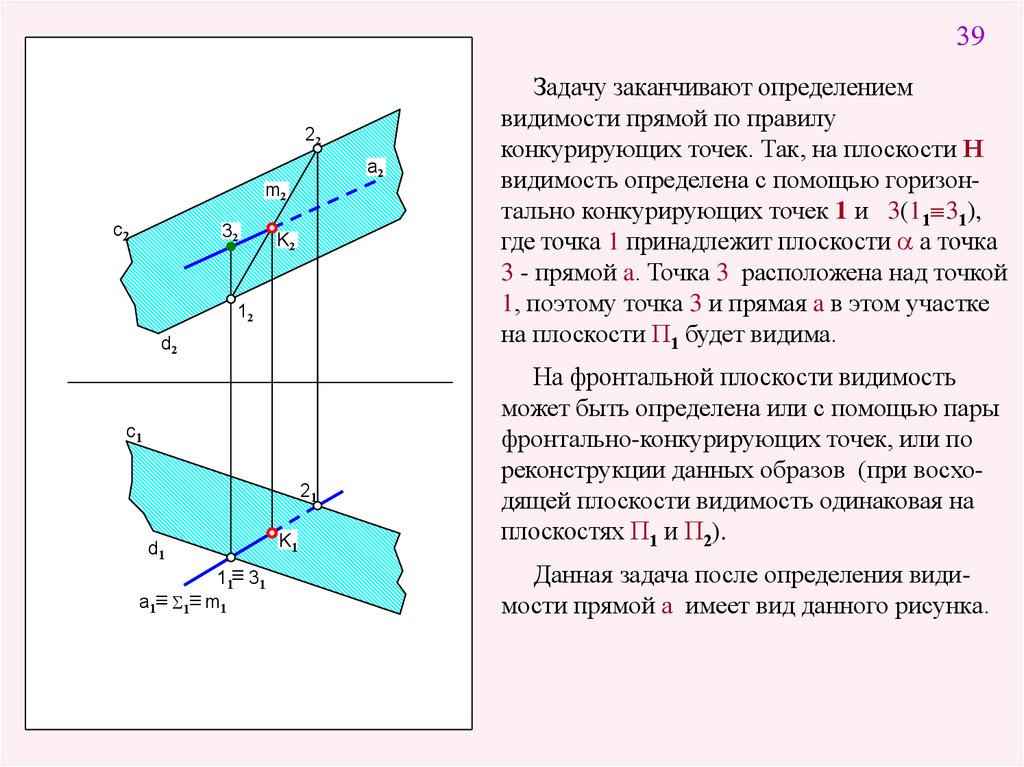
3922
a2
m2
c2
32
K2
12
d2
c1
21
d1
_
_
11_ 31
_
_ _
_
a1 _ S1 _ m1
K1
Задачу заканчивают определением
видимости прямой по правилу
конкурирующих точек. Так, на плоскости Н
видимость определена с помощью горизонтально конкурирующих точек 1 и 3(11 31),
где точка 1 принадлежит плоскости a а точка
3 - прямой a. Точка 3 расположена над точкой
1, поэтому точка 3 и прямая a в этом участке
на плоскости П1 будет видима.
На фронтальной плоскости видимость
может быть определена или с помощью пары
фронтально-конкурирующих точек, или по
реконструкции данных образов (при восходящей плоскости видимость одинаковая на
плоскостях П1 и П2).
Данная задача после определения видимости прямой а имеет вид данного рисунка.
11.
42Определение линии пересечения двух плоскостей общего положения
Для определения точек линии пересечения обе заданные плоскости a и b пересекают двумя
вспомогательными (параллельными между собой) плоскостями-посредник. Некоторое
упрощение можно достичь, если вспомогательные плоскости проводить через прямые,
задающие плоскость.
Рассмотрим пример. Плоскость a задана (ABC), плоскость b задана (DEK). Точки M и N,
определяющие искомую линию пересечения двух данных плоскостей найдем как точки
пересечения каких-либо двух сторон (как две прямые) треугольника ABC с плоскостью другого
треугольника DEK, т.е. дважды решим позиционную задачу на определение точки пересечения
прямой с плоскостью по рассмотренному алгоритму.
Выбор сторон треугольников произволен, так как только построением можно точно определить,
какая действительно сторона и какого треугольника пересечет плоскость другого. Выбор
плоскости-посредник также произволен, так как прямую общего положения, какими являются
все стороны треугольников ABC и DEK, можно заключить в горизонтально проецирующую
или во фронтально проецирующую плоскости.
12.
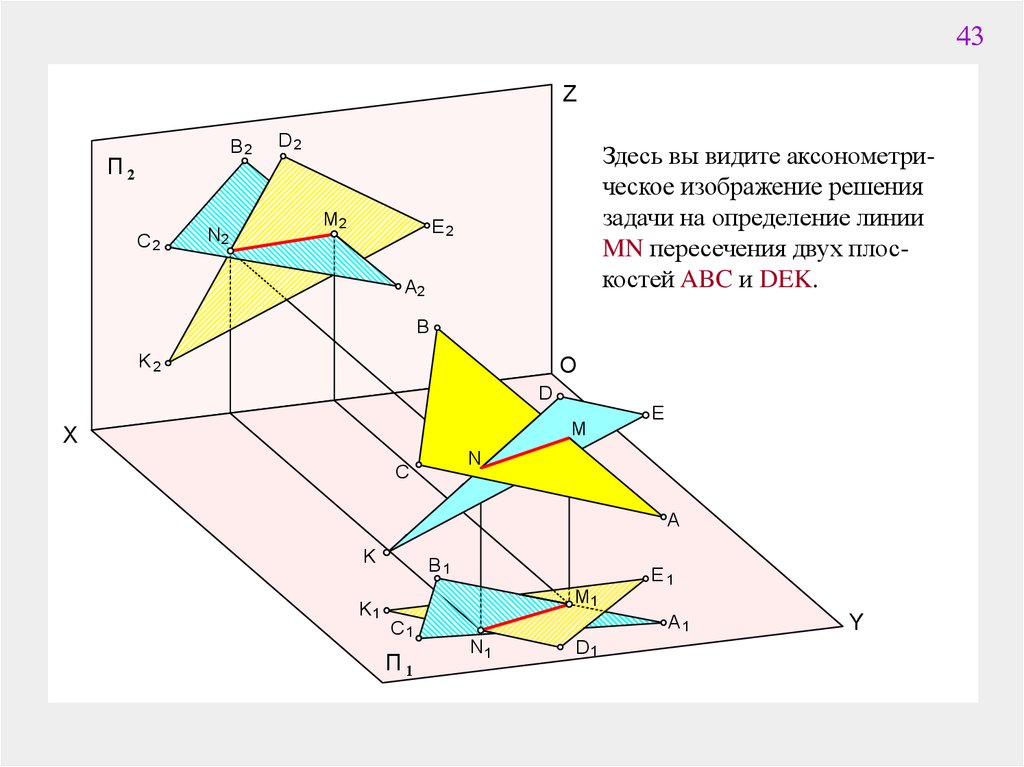
43Z
B2
П2
C2
N2
D2
M2
Здесь вы видите аксонометрическое изображение решения
задачи на определение линии
MN пересечения двух плоскостей ABC и DEK.
E2
A2
B
K2
O
D
M
X
E
N
C
A
K
B1
E1
M1
K1
A1
C1
П1
N1
D1
Y
13.
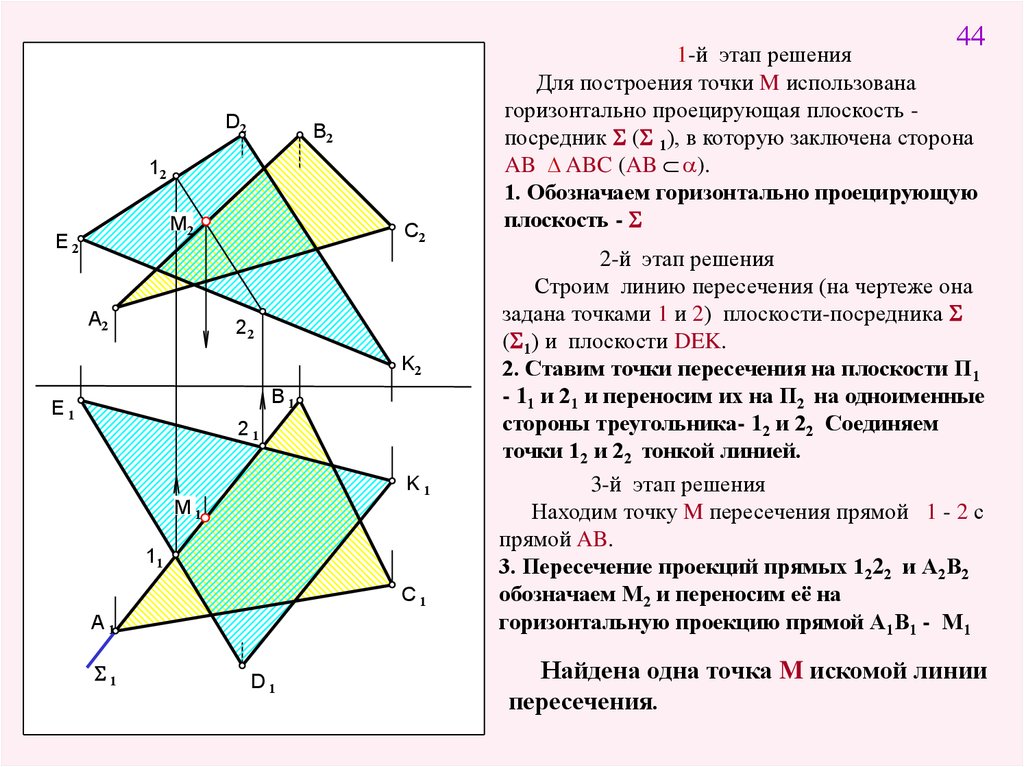
44D2
B2
12
M2
E2
A2
C2
22
K2
B1
E1
21
K1
M1
11
C1
A1
S1
D1
1-й этап решения
Для построения точки M использована
горизонтально проецирующая плоскость посредник S (S 1), в которую заключена сторона
AB ∆ ABC (AB a).
1. Обозначаем горизонтально проецирующую
плоскость - S
2-й этап решения
Строим линию пересечения (на чертеже она
задана точками 1 и 2) плоскости-посредника S
(S1) и плоскости DEK.
2. Ставим точки пересечения на плоскости П1
- 11 и 21 и переносим их на П2 на одноименные
стороны треугольника- 12 и 22 Соединяем
точки 12 и 22 тонкой линией.
3-й этап решения
Находим точку M пересечения прямой 1 - 2 с
прямой AB.
3. Пересечение проекций прямых 1222 и А2В2
обозначаем М2 и переносим её на
горизонтальную проекцию прямой А1В1 - М1
Найдена одна точка M искомой линии
пересечения.
14.
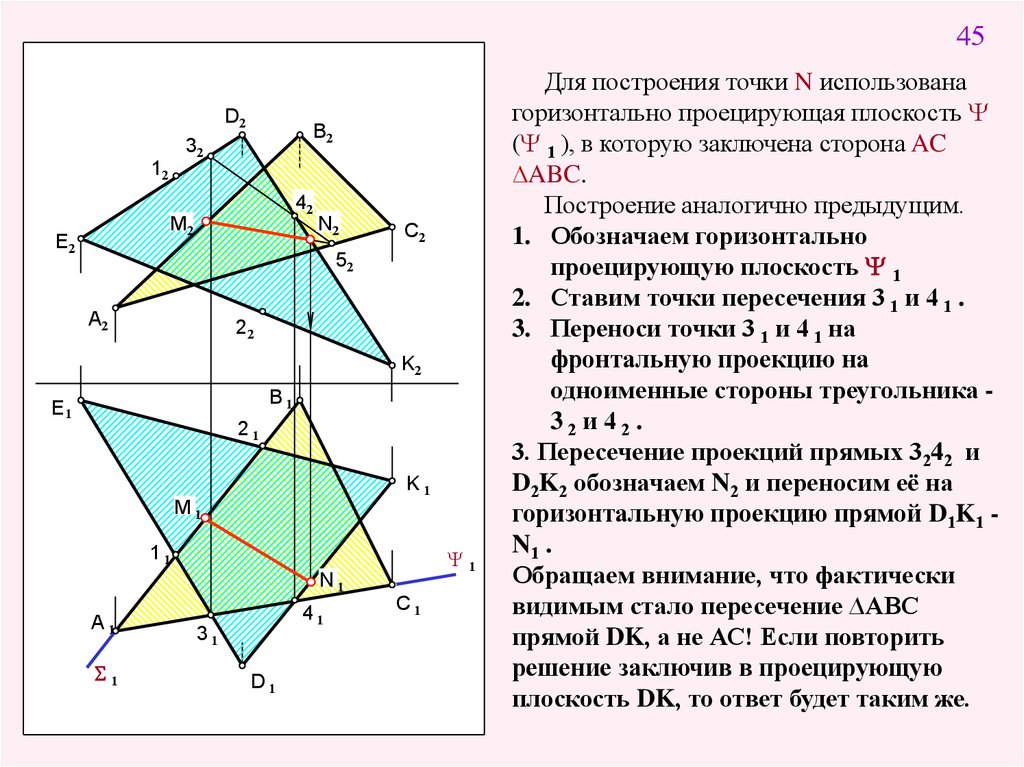
45D2
B2
32
12
42
M2
E2
N2
C2
52
A2
22
K2
B1
E1
21
K1
M1
11
1
N1
A1
S1
41
31
D1
C1
Для построения точки N использована
горизонтально проецирующая плоскость
( 1 ), в которую заключена сторона AC
∆ABC.
Построение аналогично предыдущим.
1. Обозначаем горизонтально
проецирующую плоскость 1
2. Ставим точки пересечения 3 1 и 4 1 .
3. Переноси точки 3 1 и 4 1 на
фронтальную проекцию на
одноименные стороны треугольника 32 и 42 .
3. Пересечение проекций прямых 3242 и
D2K2 обозначаем N2 и переносим её на
горизонтальную проекцию прямой D1K1 N1 .
Обращаем внимание, что фактически
видимым стало пересечение ∆ABC
прямой DK, а не АС! Если повторить
решение заключив в проецирующую
плоскость DK, то ответ будет таким же.
15.
Направление взглядадля определения
видимости на П1
12
32
D2
B2
42
M2
E2
N2
C2
52
_
_7
62 _
2
82
A2
22
K2
E1
B1
71
21
K1
M1
11
61
A1
S1
1
N1
_
_
41_ 81
31
D1
C1
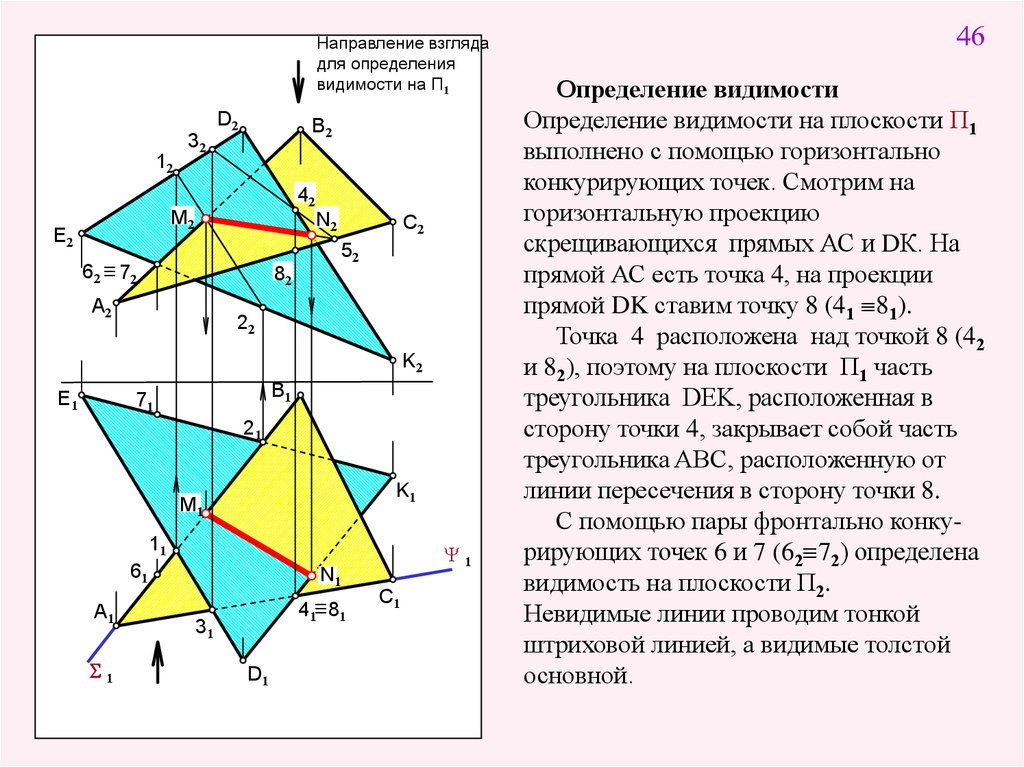
46
Определение видимости
Определение видимости на плоскости П1
выполнено с помощью горизонтально
конкурирующих точек. Смотрим на
горизонтальную проекцию
скрещивающихся прямых АС и DК. На
прямой АС есть точка 4, на проекции
прямой DK ставим точку 8 (41 81).
Точка 4 расположена над точкой 8 (42
и 82), поэтому на плоскости П1 часть
треугольника DEK, расположенная в
сторону точки 4, закрывает собой часть
треугольника ABC, расположенную от
линии пересечения в сторону точки 8.
С помощью пары фронтально конкурирующих точек 6 и 7 (62 72) определена
видимость на плоскости П2.
Невидимые линии проводим тонкой
штриховой линией, а видимые толстой
основной.
16.
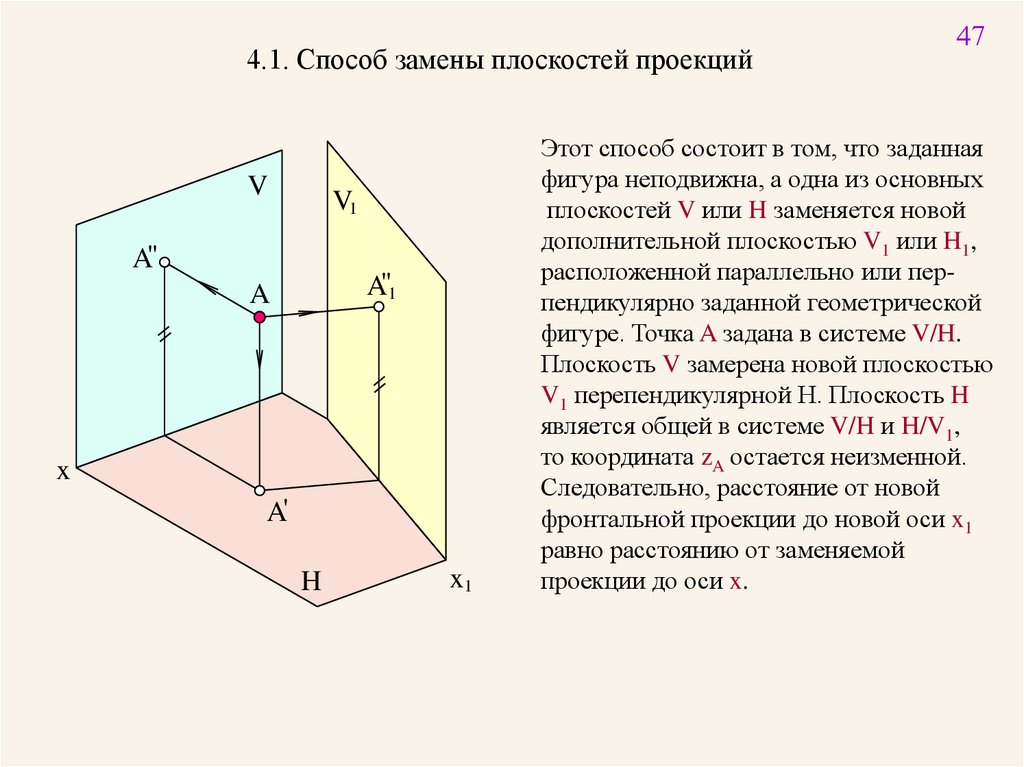
4.1. Способ замены плоскостей проекцийV
V1
A"
A"1
A
x
A'
H
x1
47
Этот способ состоит в том, что заданная
фигура неподвижна, а одна из основных
плоскостей V или H заменяется новой
дополнительной плоскостью V1 или H1,
расположенной параллельно или перпендикулярно заданной геометрической
фигуре. Точка A задана в системе V/H.
Плоскость V замерена новой плоскостью
V1 перепендикулярной H. Плоскость H
является общей в системе V/H и H/V1,
то координата zA остается неизменной.
Следовательно, расстояние от новой
фронтальной проекции до новой оси x1
равно расстоянию от заменяемой
проекции до оси x.
17.
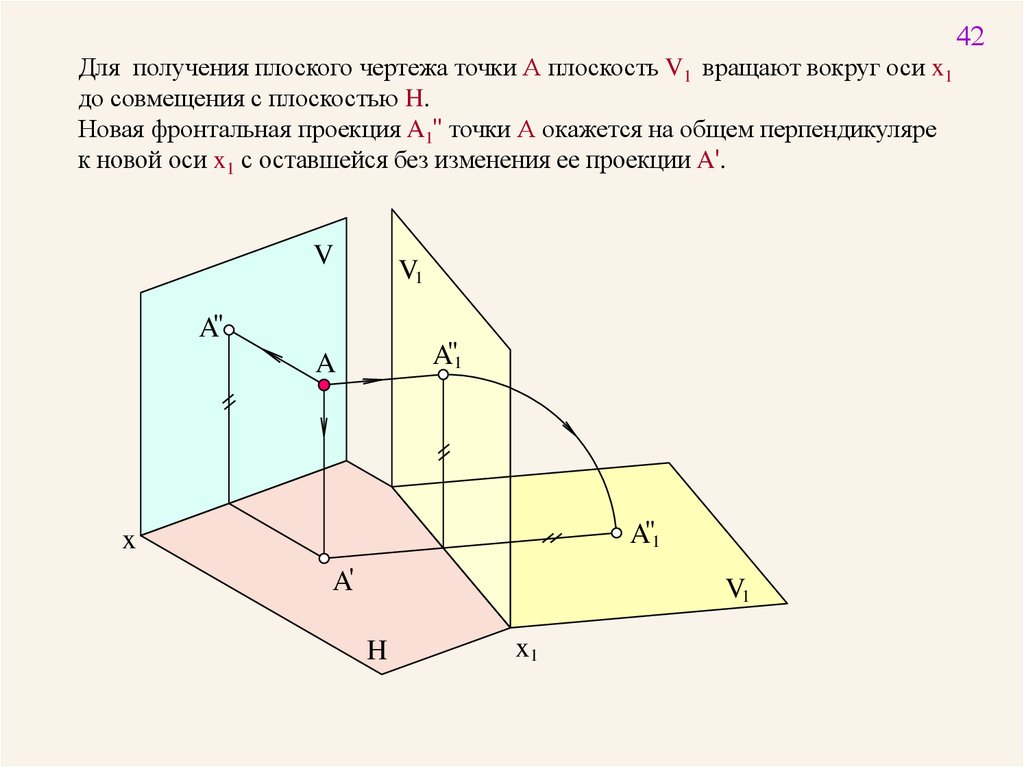
42Для получения плоского чертежа точки А плоскость V1 вращают вокруг оси x1
до совмещения с плоскостью H.
Новая фронтальная проекция A1" точки А окажется на общем перпендикуляре
к новой оси x1 с оставшейся без изменения ее проекции A'.
V
V1
A"
A"1
A
A"1
x
A'
V1
H
x1
18.
Решение четырех основных задач способом заменыплоскостей проекций
Задача 1.
Преобразовать чертеж так, чтобы
прямая общего положения оказалась
параллельной одной из плоскостей
проекций
V
A"1
A
A"
44
V1
a "1
a"
B"
a
A'
a'
H
B"1
B
B'
x1
x
Новую проекцию прямой, отвечающую поставленной задачи, можно построить на
новой плоскости проекций V1 , расположив ее параллельно самой прямой и перпендикулярно плоскости H, т.е. от системы плоскостей V/H с осью проекций x следует
перейти к системе H/V1 с новой осью x1.
19.
B"= н.в.
a"
45
a'1
b
A"
xV
H
B'1
A'1
A'
a'
x1 H
V1
A"1
H1
x1 V
B"
B'
A"
a
= н.в.
a"1
B"1
а)
x
V
H
A'
a'
б)
B'
На плоском чертеже новая ось x1 проведена параллельно a', новые линии связи A'A1"
и B'B1" проведены перпендикулярно оси x1. Новые фронтальные проекции A1" и B1"
точек A и B получают, измерив от оси x на поле V координаты высот zA и zB,
отложив их от оси x1 на новое поле V1.
Новая проекция a1" дает натуральную величину отрезка AB и угол a наклона его
к плоскости H.
Угол наклона прямой a к плоскости V можно определить, построив изображение
прямой на другой дополнительной плоскости H1 V, где H1// a.
20.
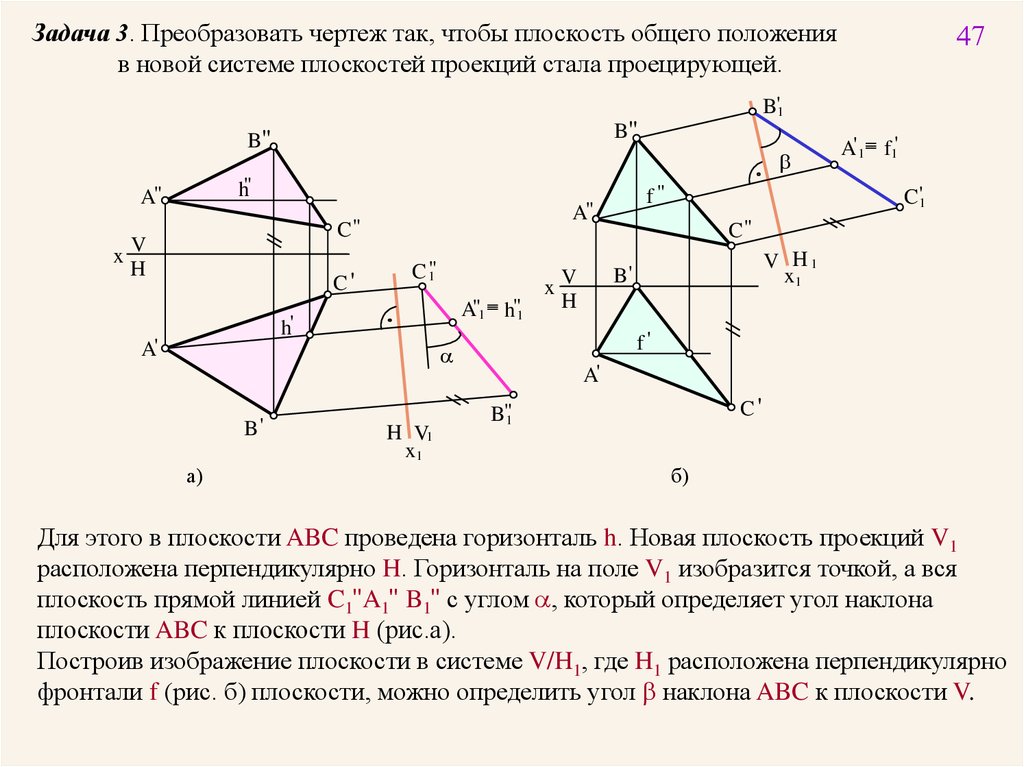
47Задача 3. Преобразовать чертеж так, чтобы плоскость общего положения
в новой системе плоскостей проекций стала проецирующей.
B'1
B"
B"
b
h"
A"
C"
xV
H
C'
C "1
_
A"1 _ h"1
h'
A'
а)
H V1
x1
C '1
C"
V H1
x1
B'
xV
H
f'
a
B'
f"
A"
_
A'1 _ f1'
A'
C'
B"1
б)
Для этого в плоскости ABC проведена горизонталь h. Новая плоскость проекций V1
расположена перпендикулярно H. Горизонталь на поле V1 изобразится точкой, а вся
плоскость прямой линией C1"A1" B1" с углом a, который определяет угол наклона
плоскости ABC к плоскости H (рис.а).
Построив изображение плоскости в системе V/H1, где H1 расположена перпендикулярно
фронтали f (рис. б) плоскости, можно определить угол b наклона ABC к плоскости V.
21.
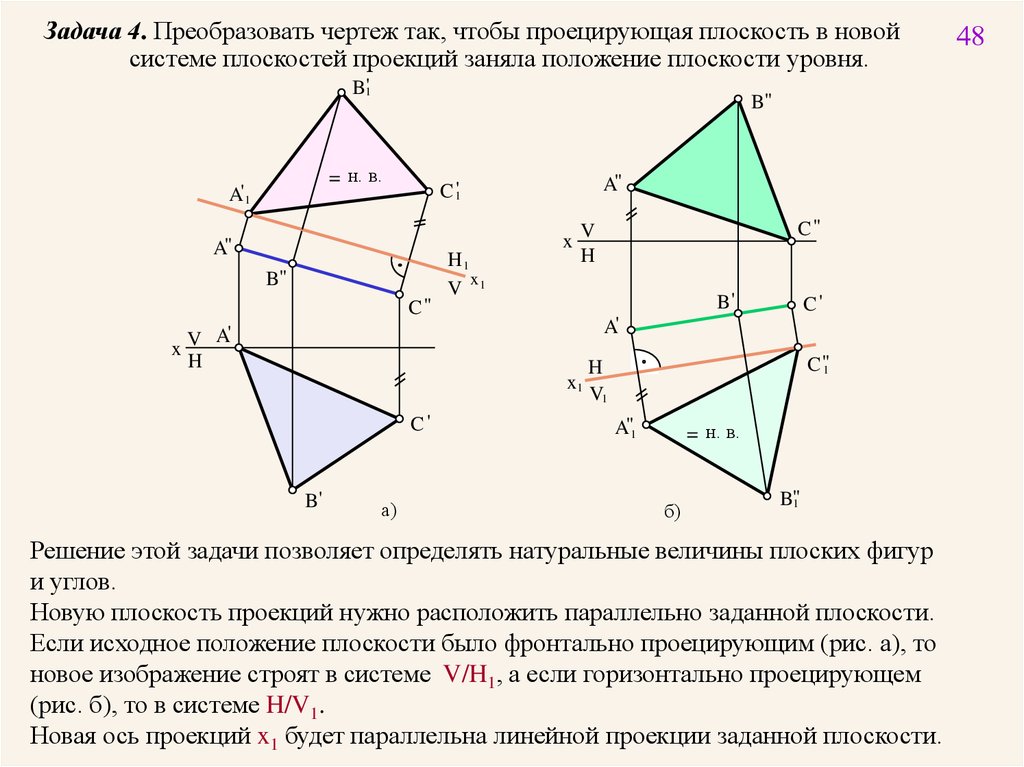
Задача 4. Преобразовать чертеж так, чтобы проецирующая плоскость в новойсистеме плоскостей проекций заняла положение плоскости уровня.
B1'
B"
= н. в.
A'1
A"
C 1'
A"
B"
C"
A'
xV
H
H1
x
V 1
C"
x V
H
B'
C'
A'
C "1
H
x1
V1
C'
B'
а)
A"1
= н. в.
б)
B"1
Решение этой задачи позволяет определять натуральные величины плоских фигур
и углов.
Новую плоскость проекций нужно расположить параллельно заданной плоскости.
Если исходное положение плоскости было фронтально проецирующим (рис. а), то
новое изображение строят в системе V/H1, а если горизонтально проецирующем
(рис. б), то в системе H/V1.
Новая ось проекций x1 будет параллельна линейной проекции заданной плоскости.
48








 Математика
Математика








