Понятие предела функции

1. Понятие предела функции

Понятие предела. Свойства
пределов. Вычисление предела
функции. Раскрытие
неопределенности.
Замечательные пределы (I, II)

2.

• Бесконечность — используется для
характеристики безграничных,
беспредельных, неисчерпаемых предметов и
явлений, в нашем случае характеристика
чисел.
• Бесконечность –сколь угодно большое
(малое), безграничное число.
Если рассмотреть координатную плоскость то
ось абсцисс (ординат) уходит на
бесконечность, если ее безгранично
продолжать влево или вправо (вниз или
вверх).

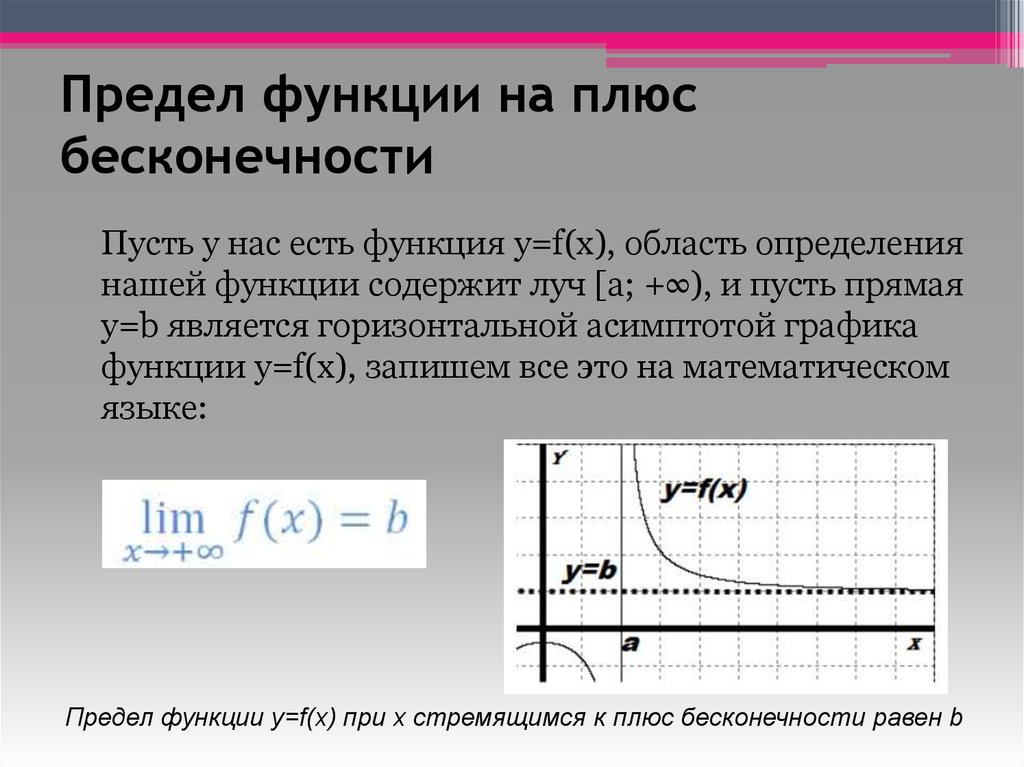
3. Предел функции на плюс бесконечности

Пусть у нас есть функция y=f(x), область определения
нашей функции содержит луч [a; +∞), и пусть прямая
y=b является горизонтальной асимптотой графика
функции y=f(x), запишем все это на математическом
языке:
Предел функции y=f(x) при x стремящимся к плюс бесконечности равен b

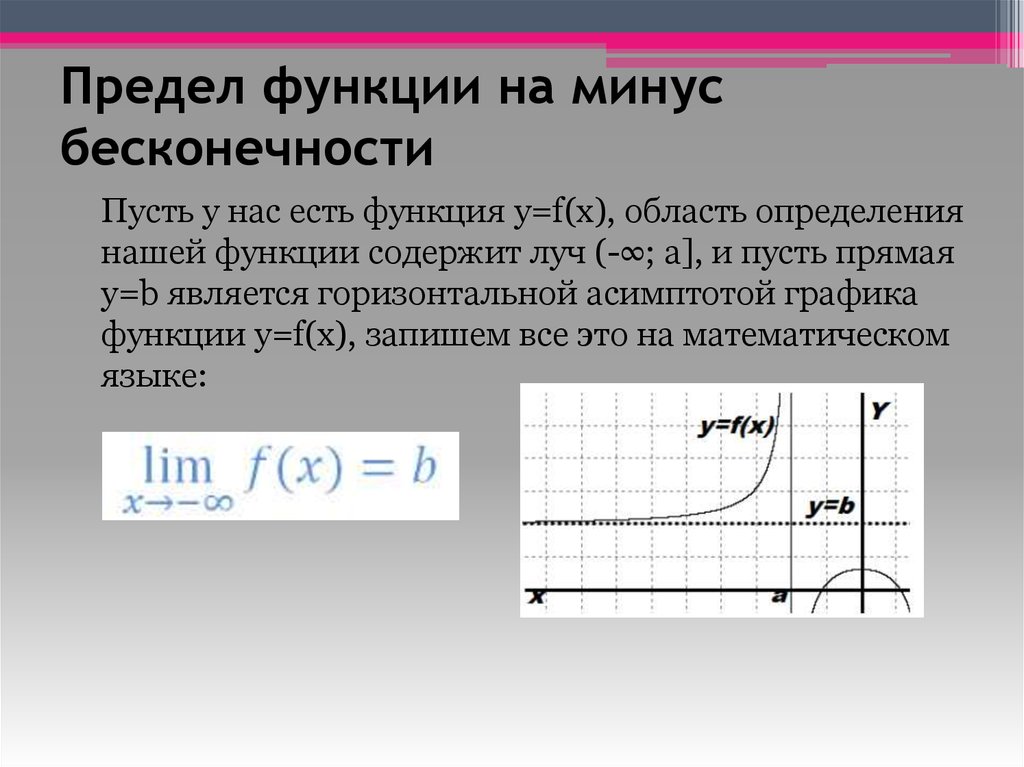
4. Предел функции на минус бесконечности

Пусть у нас есть функция y=f(x), область определения
нашей функции содержит луч (-∞; a], и пусть прямая
y=b является горизонтальной асимптотой графика
функции y=f(x), запишем все это на математическом
языке:

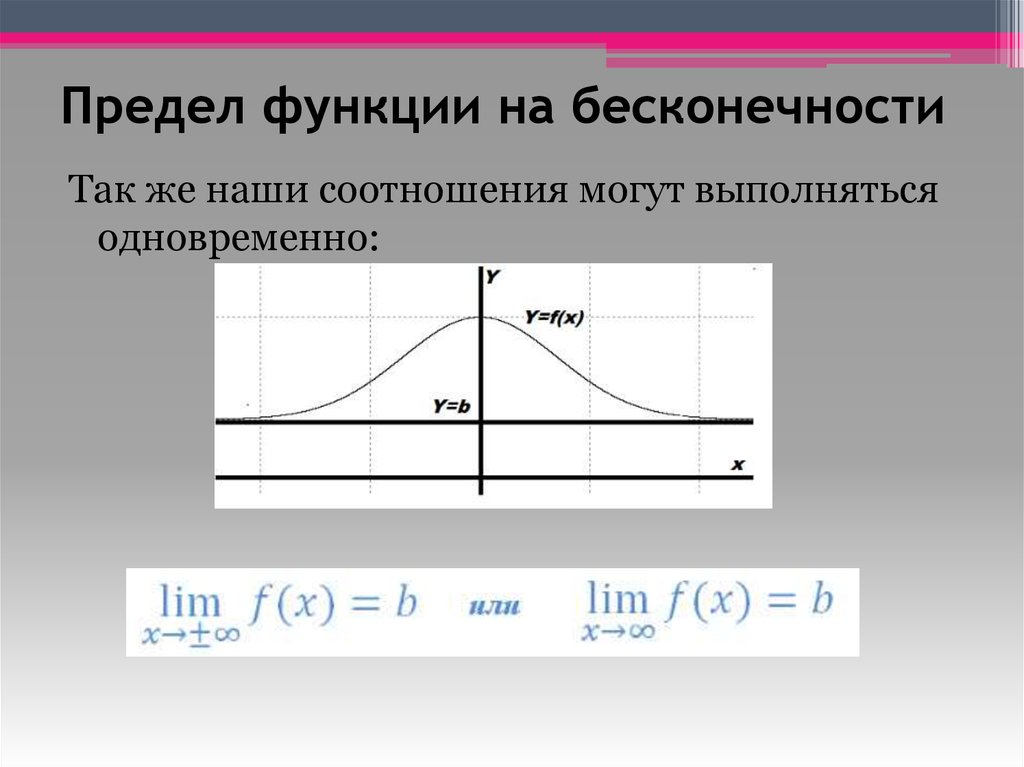
5. Предел функции на бесконечности

Так же наши соотношения могут выполняться
одновременно:

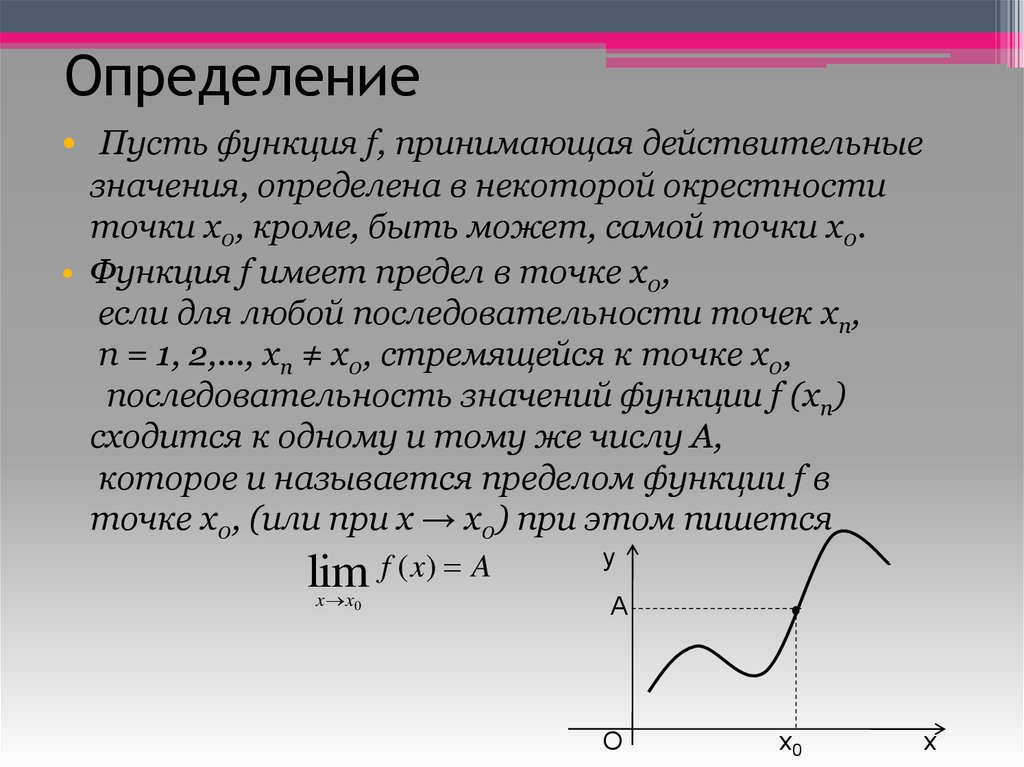
6. Определение

• Пусть функция f, принимающая действительные
значения, определена в некоторой окрестности
точки x0, кроме, быть может, самой точки x0.
• Функция f имеет предел в точке x0,
если для любой последовательности точек xn,
n = 1, 2,..., xn ≠ x0, стремящейся к точке x0,
последовательность значений функции f (xn)
сходится к одному и тому же числу А,
которое и называется пределом функции f в
точке x0, (или при x → x0) при этом пишется
lim
x x0
f ( x) A
у
А
О
х0
х

7. Определение

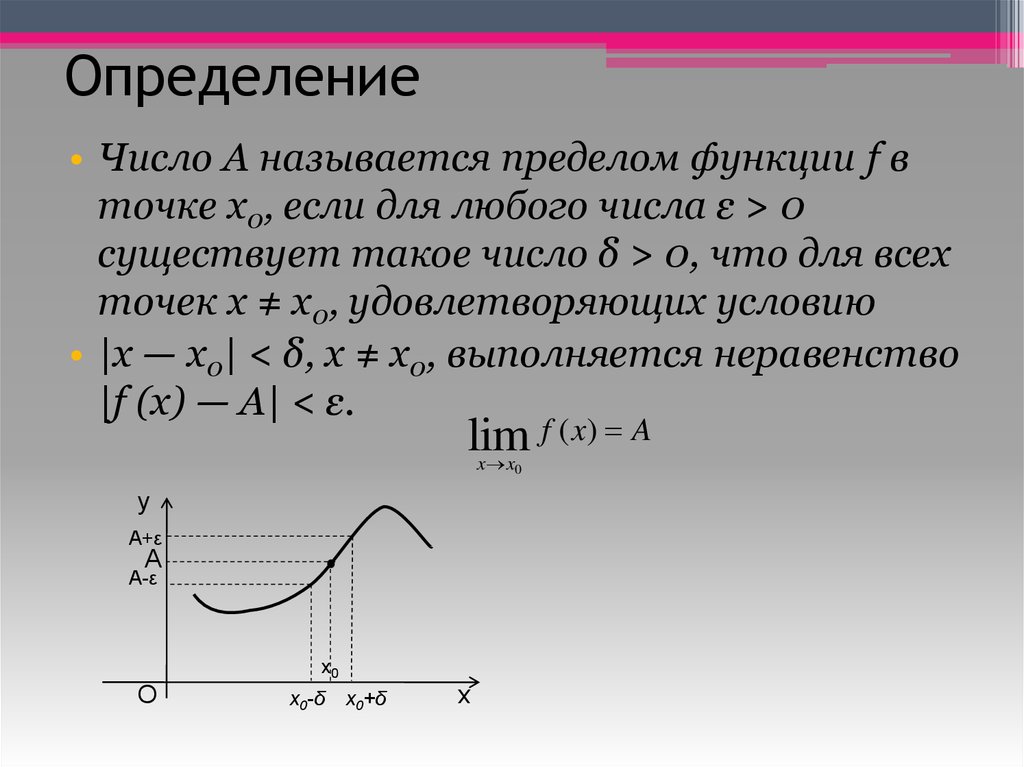
• Число А называется пределом функции f в
точке x0, если для любого числа ε > 0
существует такое число δ > 0, что для всех
точек х ≠ x0, удовлетворяющих условию
• |х — x0| < δ, x ≠ x0, выполняется неравенство
|f (x) — A| < ε.
lim f ( x) A
x x0
у
А+ε
А
А-ε
О
х0
х0-δ
х0+δ
х

8.

• Все основные элементарные функции:
постоянные, степенная функция (хα),
показательная функция (ax),
тригонометрические функции
(sinx, cosx, tgx и ctgx) и обратные
тригонометрические функции
(arcsinx, arccosx, arctgx и arcctgx) во всех
внутренних точках своих областей
определения имеют пределы, совпадающие с
их значениями в этих точках.

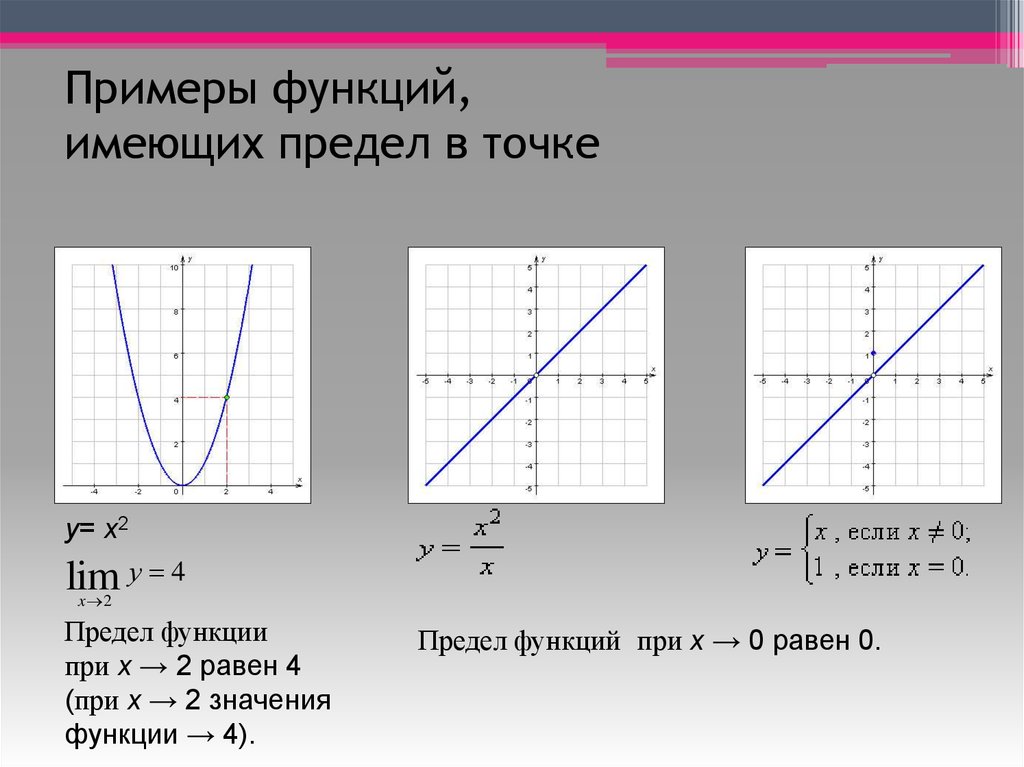
9. Примеры функций, имеющих предел в точке

у= x2
lim у 4
x 2
Предел функции
при x → 2 равен 4
(при x → 2 значения
функции → 4).
Предел функций при x → 0 равен 0.

10.

Примеры функций,
не имеющих предел в точке
у
у
у
А
1
О
х
-1
О
а
х
О
а
х

11. Свойства предела функции в точке

Если функции f (x) и g (x) имеют конечные пределы в точке a,
причем
То
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.

12. Вычисление предела функции в точке

Пример 1. Сначала просто пытаемся подставить число в функцию
lim ( x 2 5x 8) 9 15 8 2
x 3
Пример 2. Найдем
x2 5x 8
lim 2
.
x 3 x x 4
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя
lim ( x 2 x 4) 9 3 4 10
x 3
.
Используя теорему о пределе частного, получим
lim ( x 2 5 x 8)
x 5 x 8 x 3
2 1
lim 2
.
2
x 3 x x 4
lim ( x x 4) 10 5
2
x 3

13.

Пример 3. Найдем
x 2 5x 8
lim
.
x 3
x 3
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя равен нулю, поэтому теорему о пределе частного
применять нельзя.
Величина 1/(x-3) является бесконечно большой величиной при x→3.
Тогда
x 2 5x 8
lim
.
x 3
x 3

14. Раскрытие неопределенности

• При нахождении предела иногда сталкиваются с
неопределенностями вида
0
0
0
, , ( ), (1 ), (0 ), (0 )( ).
0
• Отыскание предела в таких случаях называется
раскрытием неопределенности.
Для того, чтобы раскрыть неопределенность ∞/∞ необходимо разделить
числитель и знаменатель на х в старшей степени.
Пример 1.
Разделим числитель и знаменатель на х2

15.

Пример 2.
Разделим числитель и знаменатель на х4

16.

Пример 3.
Разделим числитель и знаменатель на х2
подразумевается не деление на ноль (делить на ноль нельзя), а деление на
бесконечно малое число.
Таким образом, при раскрытии неопределенности
может получиться конечное число, ноль или
бесконечность.

17.

Пример 4. Вычислить предел
:
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность 0/0
Общее правило: если в числителе и знаменателе находятся многочлены, и
имеется неопределенность вида 0/0, то для ее раскрытия нужно разложить
числитель и знаменатель на множители.
Очевидно, что можно сократить на (х+1)
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

18.

Метод умножения числителя и знаменателя на сопряженное выражение
Пример 5. Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела это первое,
что нужно выполнять для ЛЮБОГО предела.
Получена неопределенность вида 0/0 ,
которую нужно устранять
Когда в числителе (знаменателе) находится разность корней (или корень минус какоенибудь число), то для раскрытия неопределенности используют метод умножения
числителя и знаменателя на сопряженное выражение.

19.

20. Замечательные пределы

• первый замечательный предел
sin x
lim
1;
x 0
x
• второй замечательный предел
х
1
1
lim 1 lim (1 x) x e.
x
x 0
x

21. Примеры

sin( 2 x )
0
lim
( )
x 0
x
0
2 sin( 2 x )
sin( 2 x )
lim
2 lim
x 0
x
0
2x
2x
2 1 2.
е
4
3

22. Односторонние пределы

Предел функции слева
у
• Число A1 называется пределом
функции f (x) слева в точке a, если
для каждого ε > 0 существует δ > 0
А +ε
А1
такое, что для
А -ε
всех
выполняется
О
неравенство
1
1
а
lim f ( x) A
х а 0
• При х приближающихся к а слева,
значения функции стремятся к А1
х
а-δ
1

23. Предел функции  справа

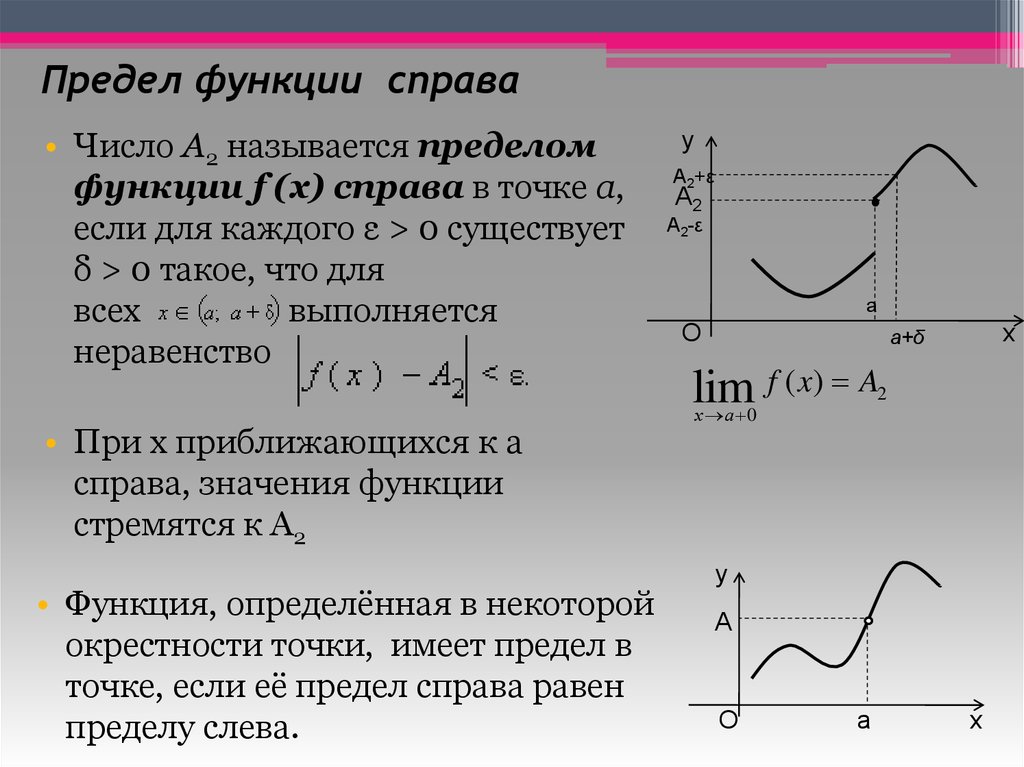
Предел функции справа
• Число A2 называется пределом
функции f (x) справа в точке a,
если для каждого ε > 0 существует
δ > 0 такое, что для
всех
выполняется
неравенство
• При х приближающихся к а
справа, значения функции
стремятся к А2
• Функция, определённая в некоторой
окрестности точки, имеет предел в
точке, если её предел справа равен
пределу слева.
у
А2+ε
А2
А2-ε
а
О
х
а+δ
lim f ( x) A
2
х а 0
у
А
О
а
х

24.

у
1
О
х
-1
lim у 1
х 0 0
lim у 0
х 0
lim у 0
х 0
lim у 1
х 0 0