Похожие презентации:
Центральные и вписанные углы
1.
2.
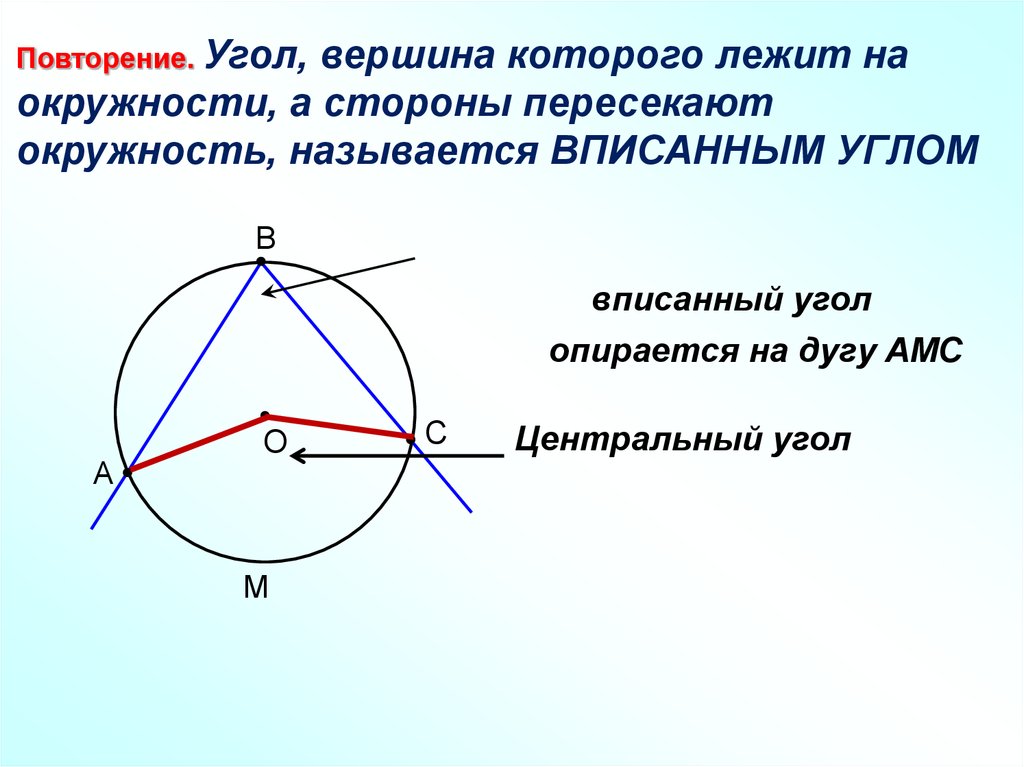
Повторение. Угол,вершина которого лежит на
окружности, а стороны пересекают
окружность, называется ВПИСАННЫМ УГЛОМ
В
вписанный угол
опирается на дугу АМС
А
О
М
С
Центральный угол
3.
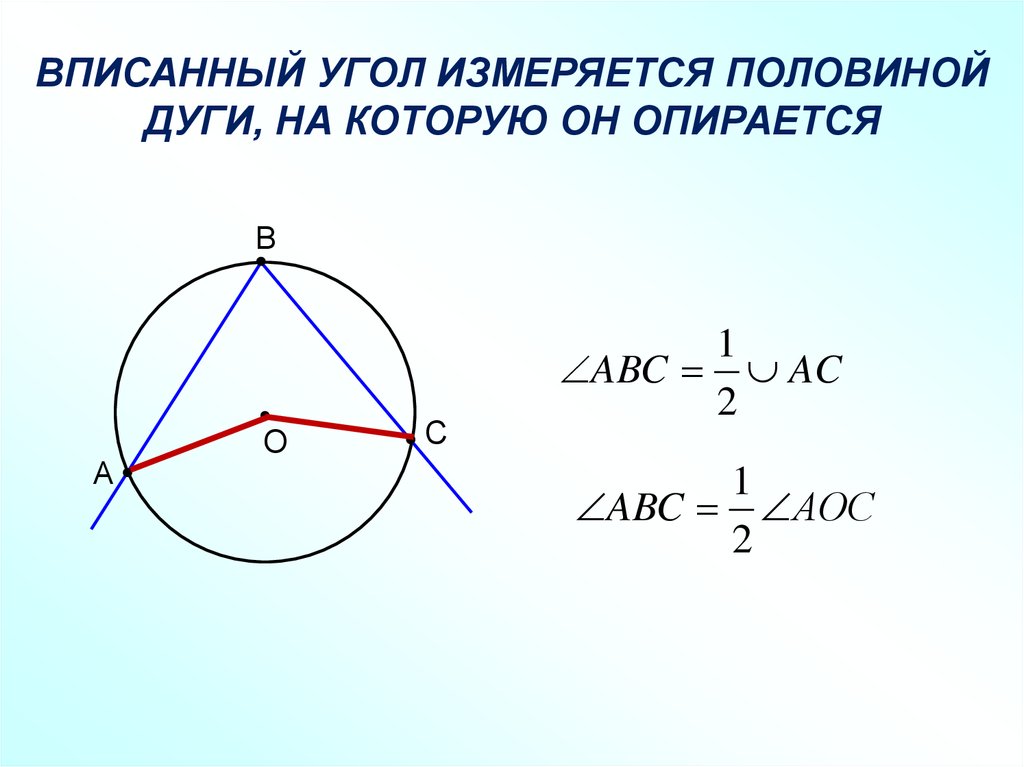
ВПИСАННЫЙ УГОЛ ИЗМЕРЯЕТСЯ ПОЛОВИНОЙДУГИ, НА КОТОРУЮ ОН ОПИРАЕТСЯ
В
А
О
С
1
ABC AC
2
1
ABC АOС
2
4.
СЛЕДСТВИЕ 1:ВПИСАННЫЕ УГЛЫ,
ОПИРАЮЩИЕСЯ НА
ОДНУ И ТУ ЖЕ ДУГУ,
РАВНЫ
СЛЕДСТВИЕ 2:
ВПИСАННЫЙ УГОЛ,
ОПИРАЮЩИЙСЯ НА
ПОЛУОКРУЖНОСТЬ,
ПРЯМОЙ
О
О
5.
Повторение. Расстояние от точки до прямой.ВМ – касательная в точке С. Найдите расстояние от
точки А до прямой ВМ.
М
С
В
?
А
6.
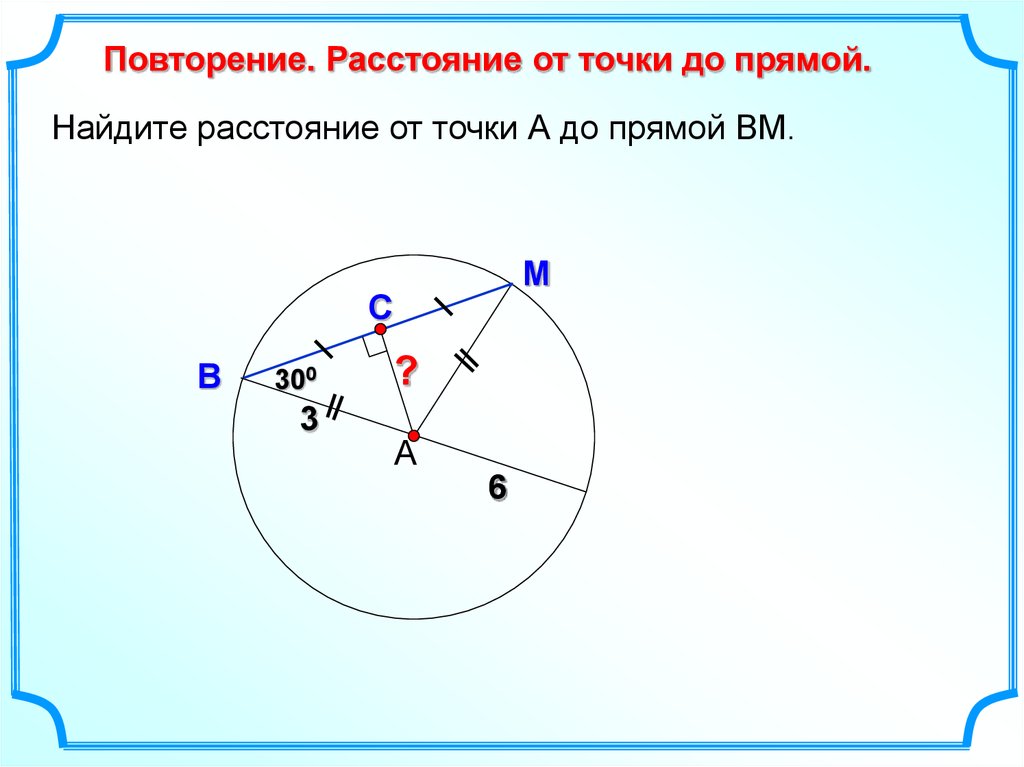
Повторение. Расстояние от точки до прямой.Найдите расстояние от точки А до прямой ВМ.
М
С
В
300
3
?
А
6
7.
Повторение. Расстояние от точки до прямой.Найдите расстояние от точки А до прямой ВМ.
ВМ = 10 см.
С 5
В
?
А
М
8.
Повторение. Расстояние от точки до прямой.Найдите расстояние от точки А до прямой ВМ.
О – центр окружности.
М
А
?
5см
10см
О
300
В
9.
Повторение. Расстояние от точки до прямой.Найдите расстояние от точки А до прямой ВМ.
ВМ = 3 см.
М
?
3см
А
О
450
В
10.
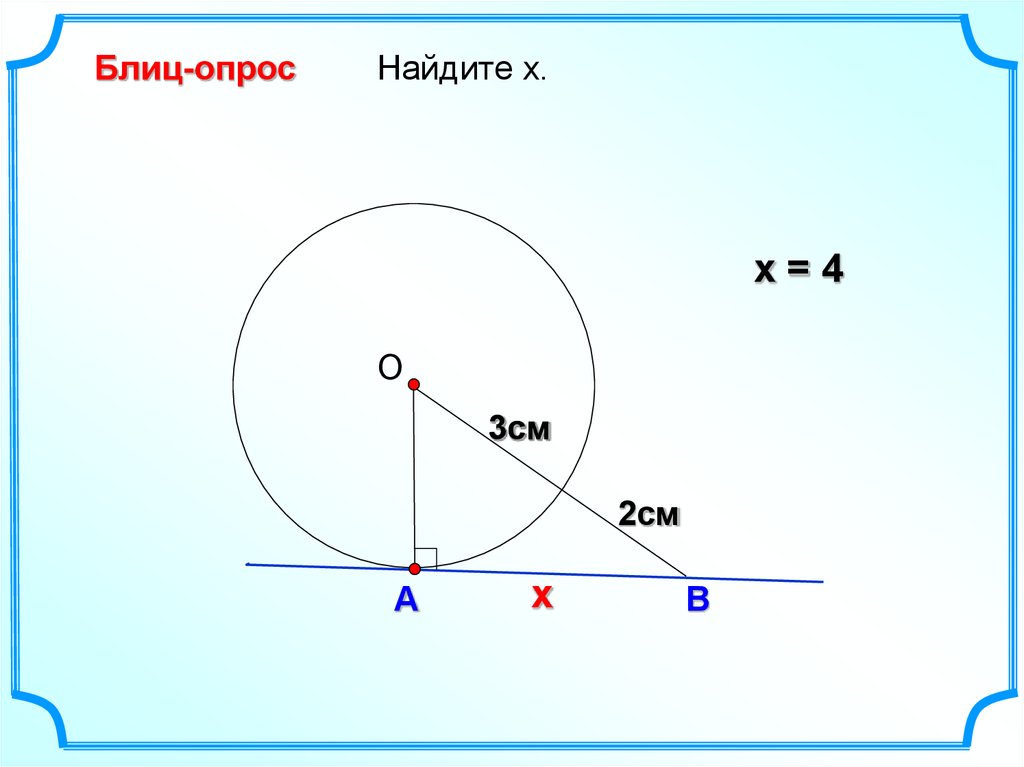
Блиц-опросНайдите х.
х=4
О
3см
2см
А
х
В
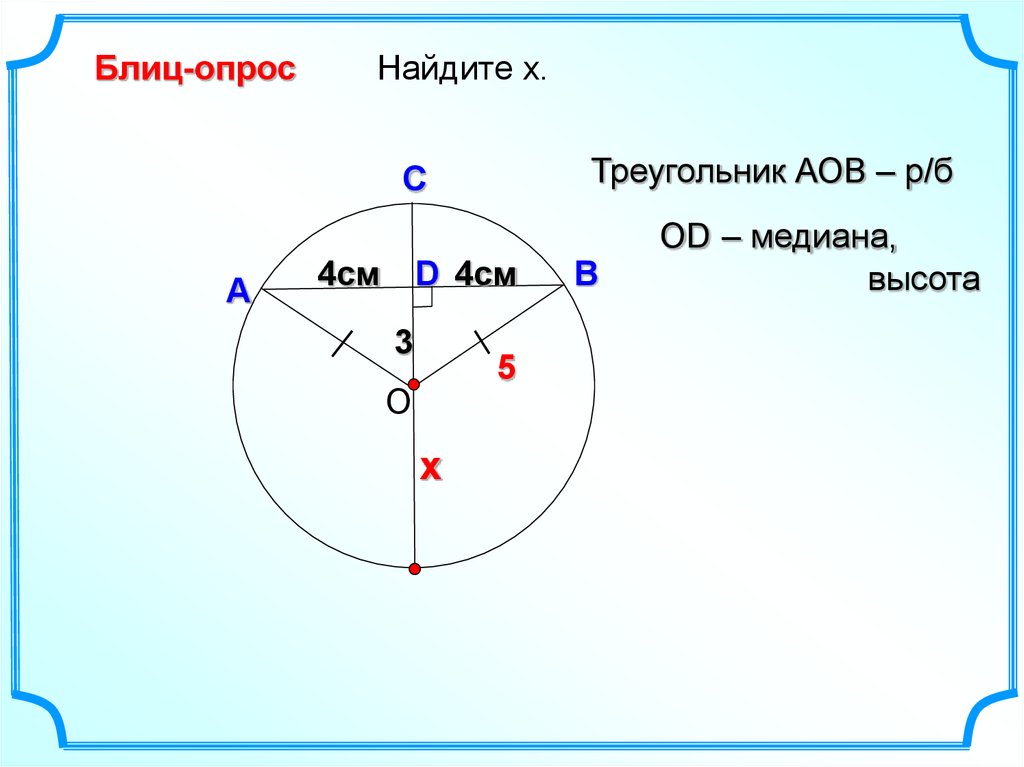
11.
Блиц-опросНайдите х.
Треугольник АОВ – р/б
С
А
4см D 4см
3
5
О
х
В
OD – медиана,
высота
12.
Блиц-опросНайдите градусную меру угла ВАС.
А
?
530
В
О
370
С
13.
Блиц-опросНайдите х.
В
3
А
х = 2,5
х
О
5
4
С
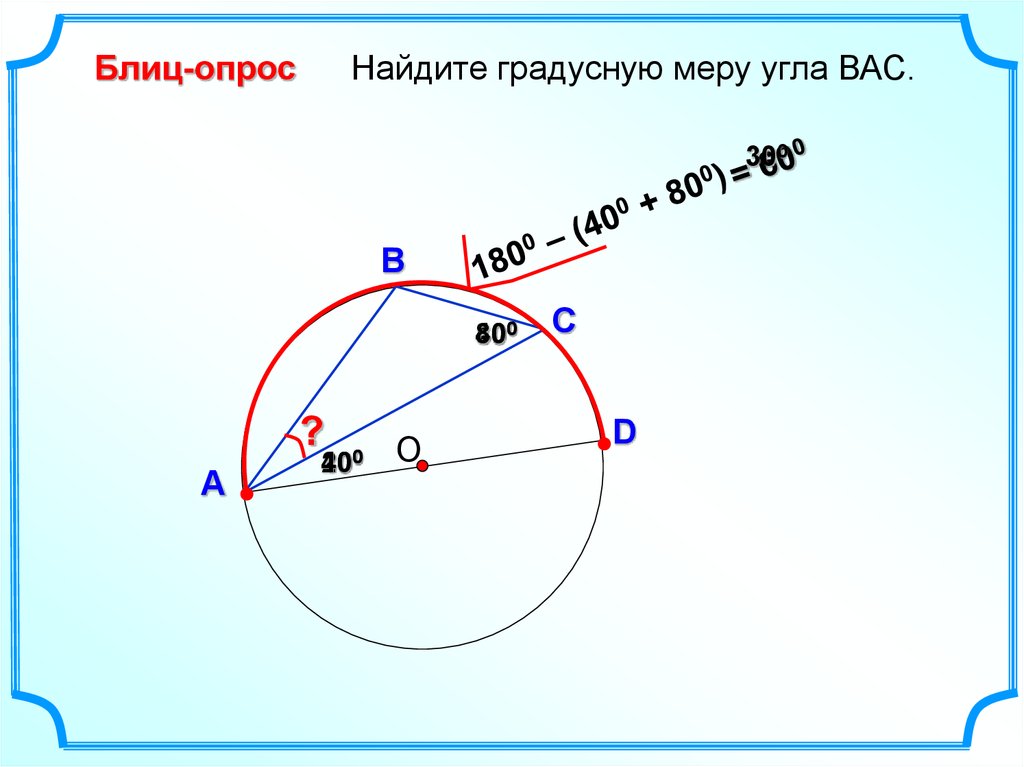
14.
Блиц-опросНайдите градусную меру угла ВАС.
300
В
800
40
?
А
200
40
О
C
D
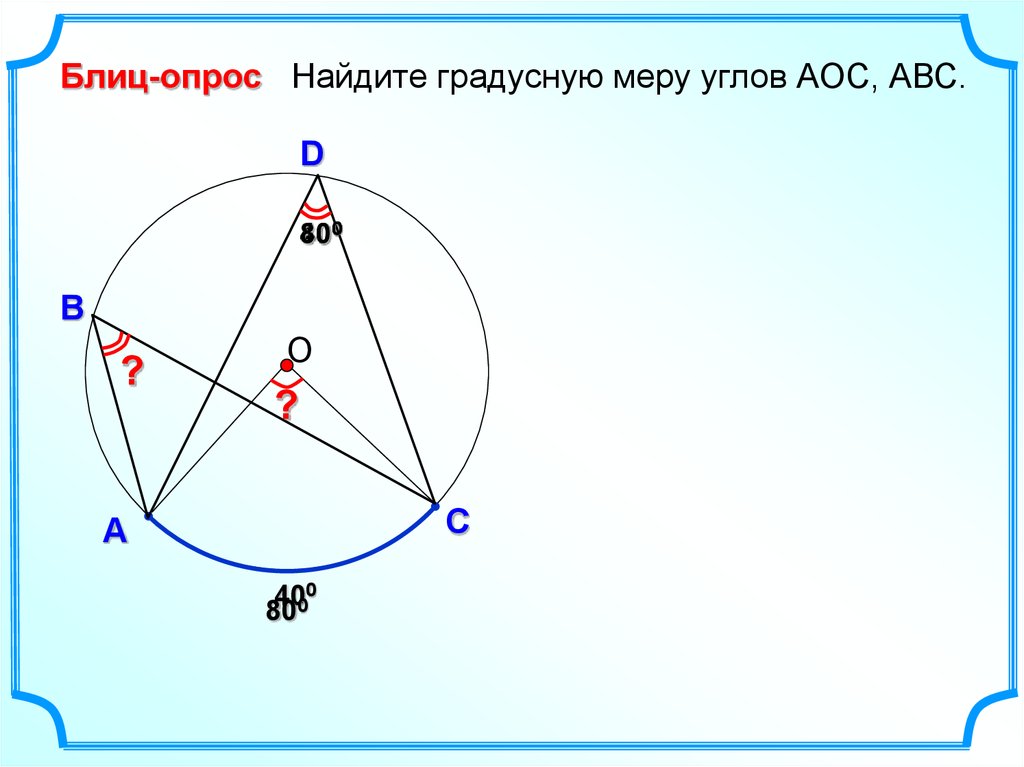
15.
Блиц-опрос Найдите градусную меру углов АОC, АВС.D
800
40
В
?
О
?
С
А
4000
80
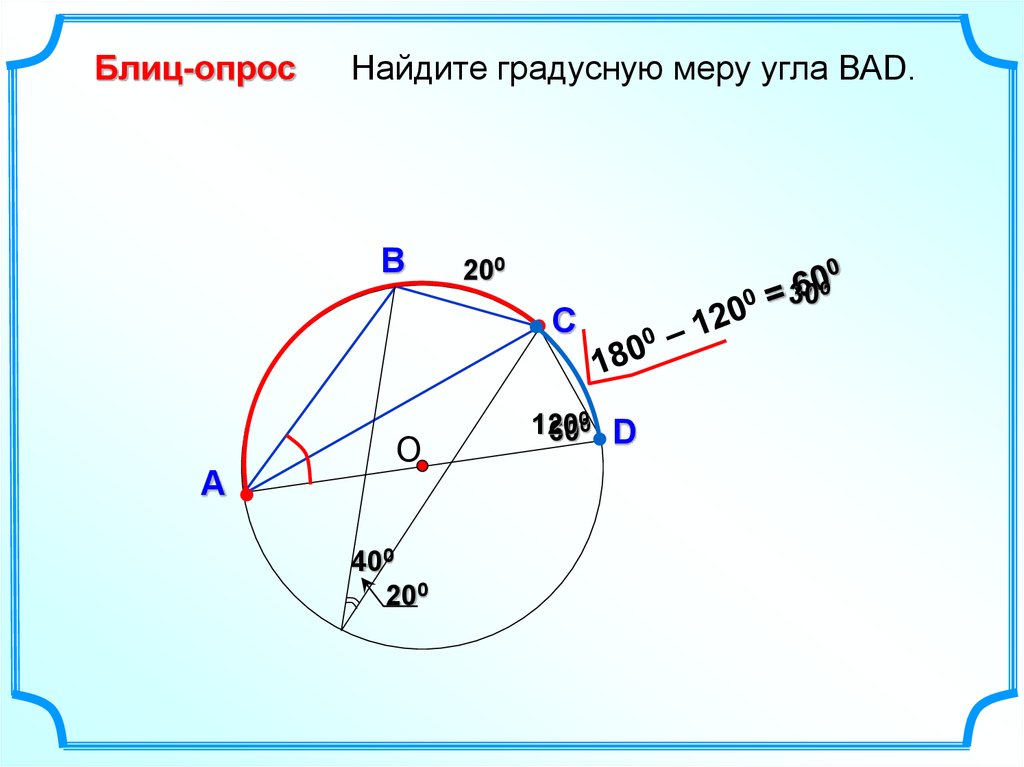
16.
Блиц-опросНайдите градусную меру угла ВАD.
В
200
C
А
О
400
200
0
120
600 D
300
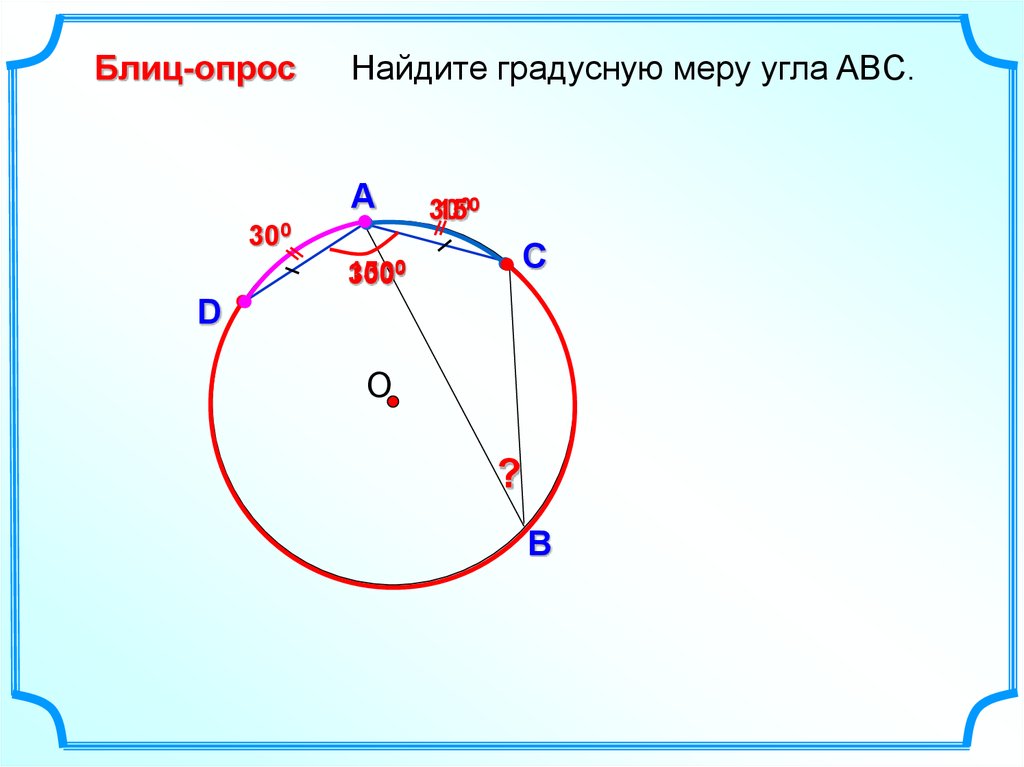
17.
Блиц-опросНайдите градусную меру угла ABC.
A
300
30
1500
C
150
3000
D
О
?
B
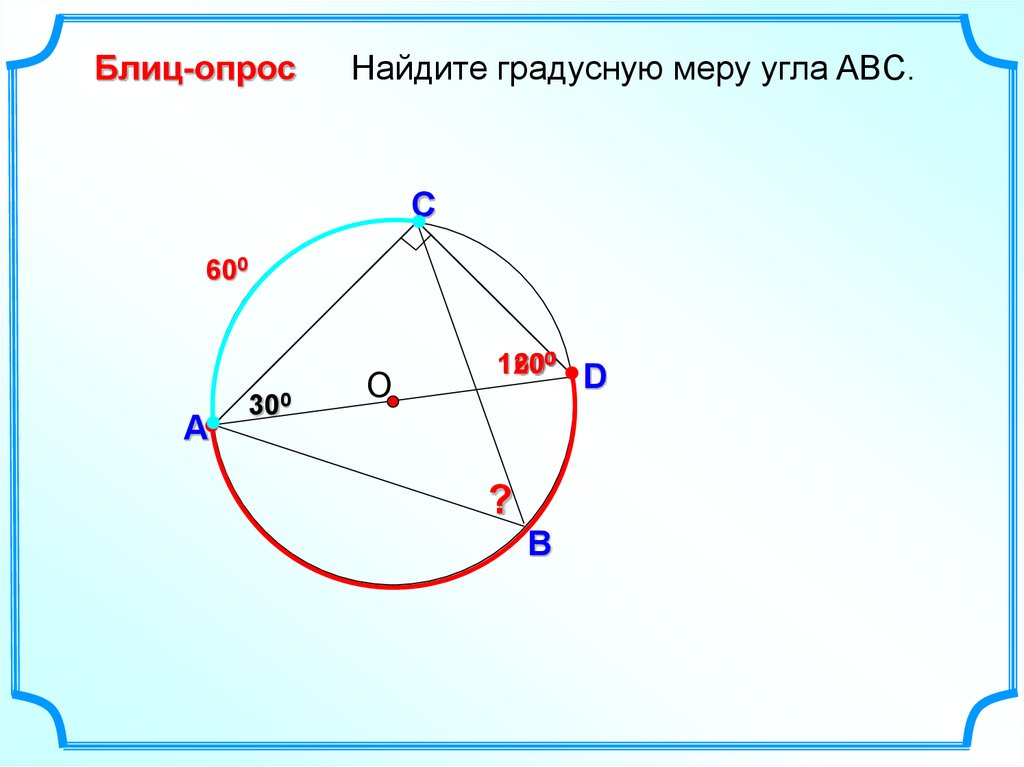
18.
Блиц-опросНайдите градусную меру угла ABC.
C
600
A
300
О
120
600 D
?
B
19.
Блиц-опросНайдите градусную меру угла ABC.
А
D
120
600 0
300
60
С
О
?
B
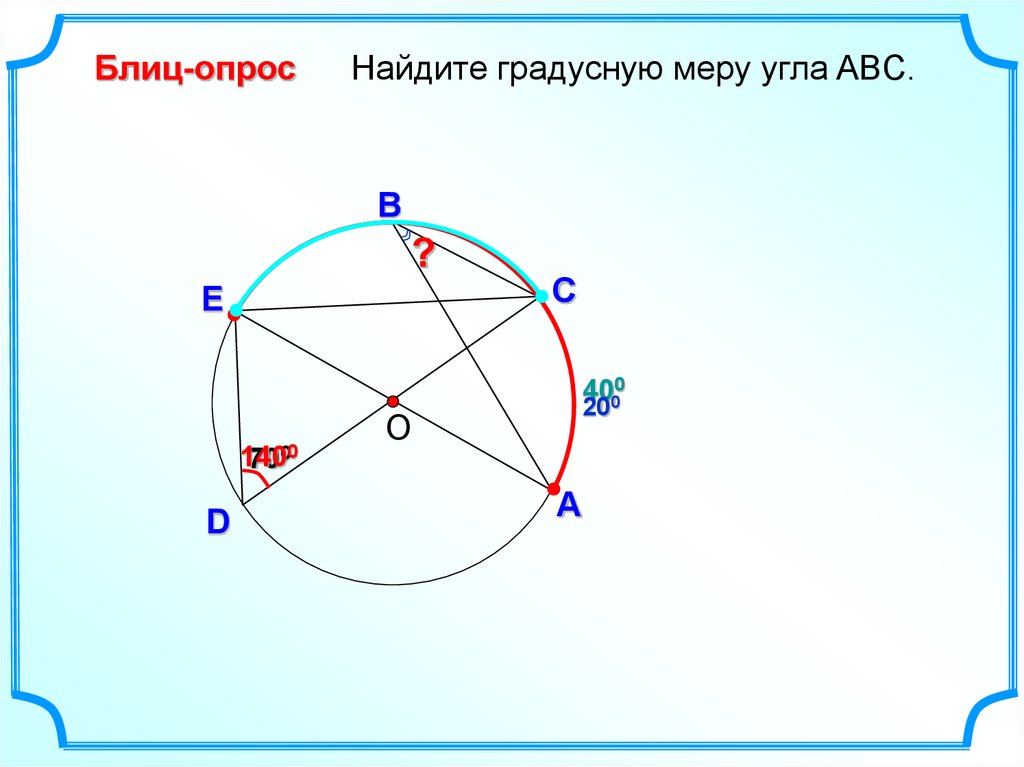
20.
Блиц-опросНайдите градусную меру угла ABC.
В
?
Е
140
7000
D
С
4000
20
О
А
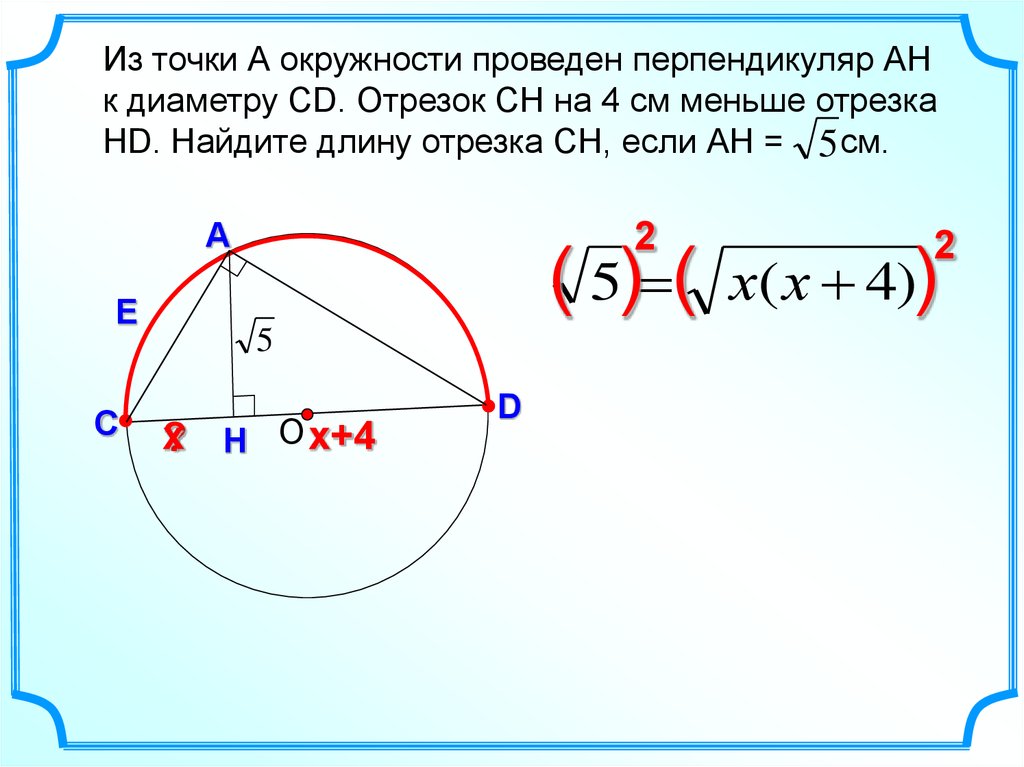
21.
Из точки А окружности проведен перпендикуляр АHк диаметру СD. Отрезок СН на 4 см меньше отрезка
НD. Найдите длину отрезка СН, если АН = 5 см.
А
Е
С
2
( 5) (
5
x
? Н О x+4
D
2
х( х 4))
22.
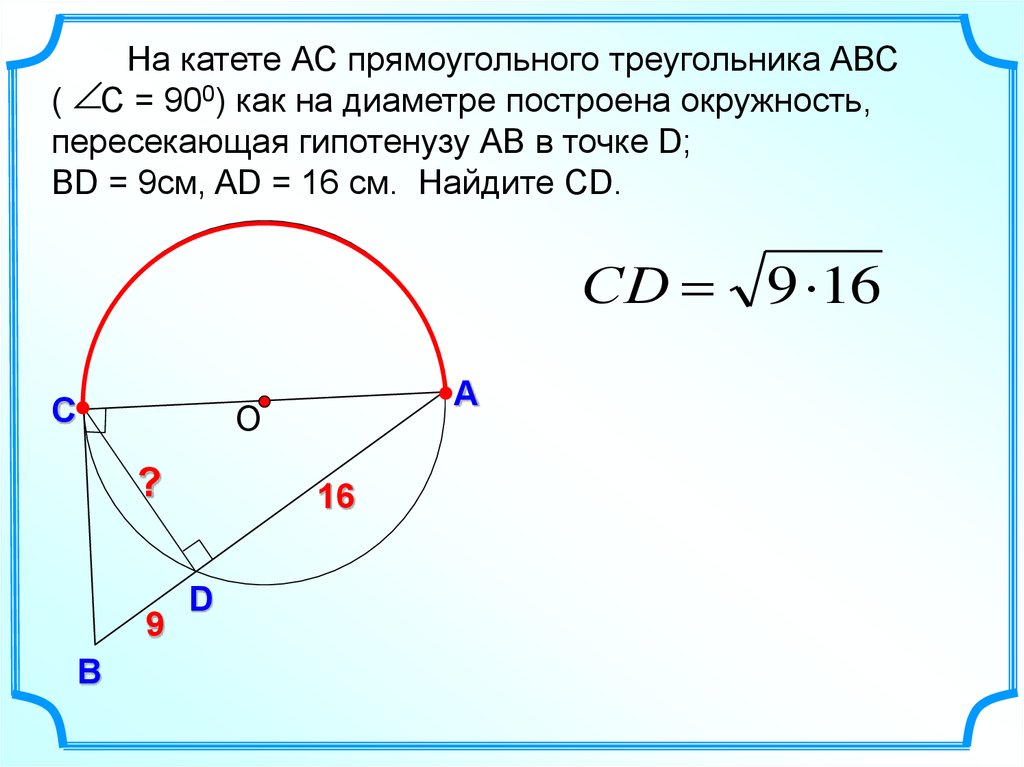
На катете АС прямоугольного треугольника АВС( С = 900) как на диаметре построена окружность,
пересекающая гипотенузу АВ в точке D;
ВD = 9см, AD = 16 см. Найдите СD.
СD 9 16
С
А
О
?
9
В
16
D
23.
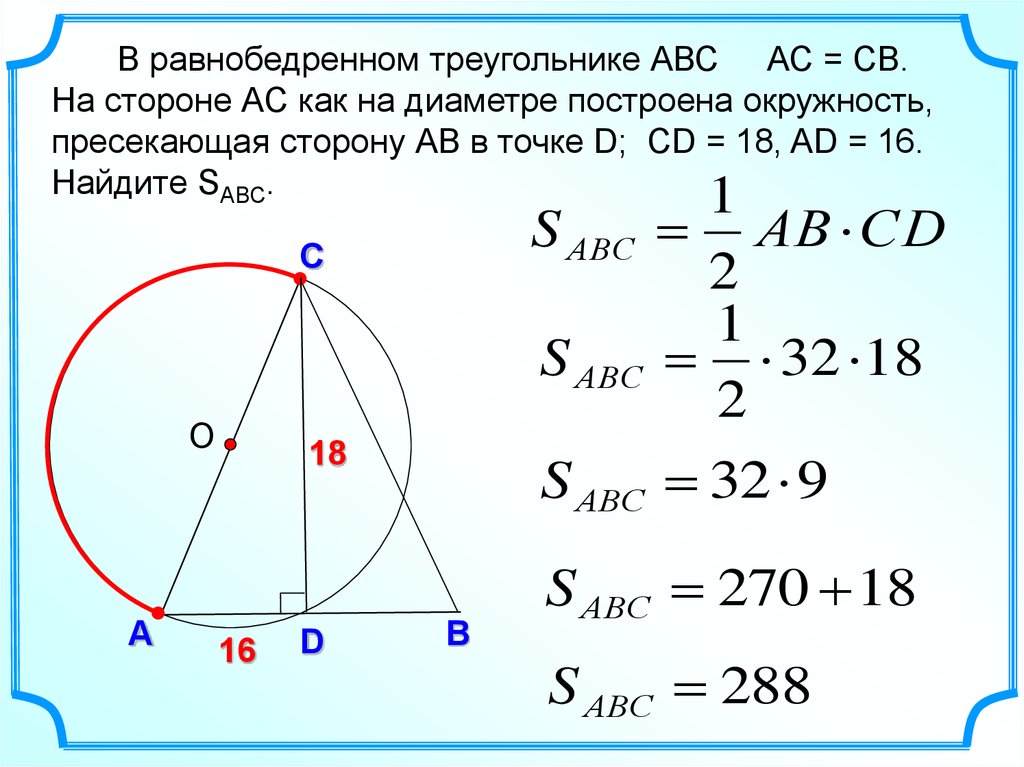
В равнобедренном треугольнике АВС АС = СВ.На стороне АС как на диаметре построена окружность,
пресекающая сторону АВ в точке D; СD = 18, AD = 16.
Найдите SАВС.
1
S АВС АВ СD
2
1
S АВС 32 18
2
С
О
А
18
16
D
S АВС 32 9
В
S АВС 270 18
S АВС 288
24.
Повторение. Подобие треугольников.Найдите пары подобных треугольников и докажите их
подобие. Запишите равенство соответствующих сторон.
ABС
В
ОЕС
по 1 признаку
Е
ОЕ
А
О
С
СЕ
ОC
1
=
=?
=
СВ
AС 2
АВ
25.
Повторение. Подобие треугольников.Найдите пары подобных треугольников и докажите их
подобие. Запишите равенство соответствующих сторон.
AB – касательная.
В
ACD
С
по 1 признаку
E
А
ОAЕ
О
D
ОЕ
АD
AЕ
=
СD
=
ОA
AС
=?
26.
Теорема о произведении отрезковпересекающихся хорд
Если две хорды пересекаются, то произведение
отрезков одной хорды равно произведению отрезков
другой хорды. Дано: АВ и CD – хорды,
С
А
1
2
4
3 E
Доказать:
AB CD E
AЕ ВЕ СE DЕ
Доказательство:
В
AЕD
по 1 признаку
АЕ
CЕ
D
CЕB
DE
=
BE
AЕ ВЕ СE DЕ
27.
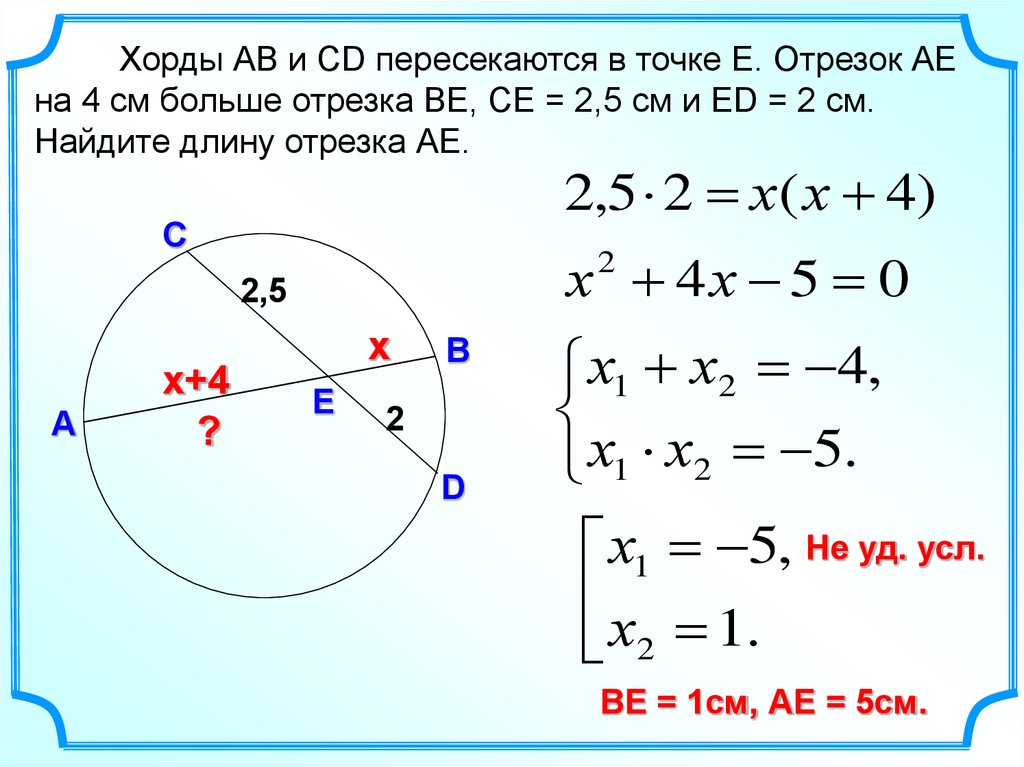
Хорды АВ и СD пересекаются в точке Е. Отрезок АЕна 4 см больше отрезка ВЕ, СЕ = 2,5 см и ЕD = 2 см.
Найдите длину отрезка АЕ.
2,5 2 х( х 4)
С
х 4х 5 0
2
2,5
А
x+4
?
x
Е
В
2
D
х1 х2 4,
х1 х2 5.
х1 5, Не уд. усл.
х 1.
2
ВЕ = 1см, АЕ = 5см.
28.
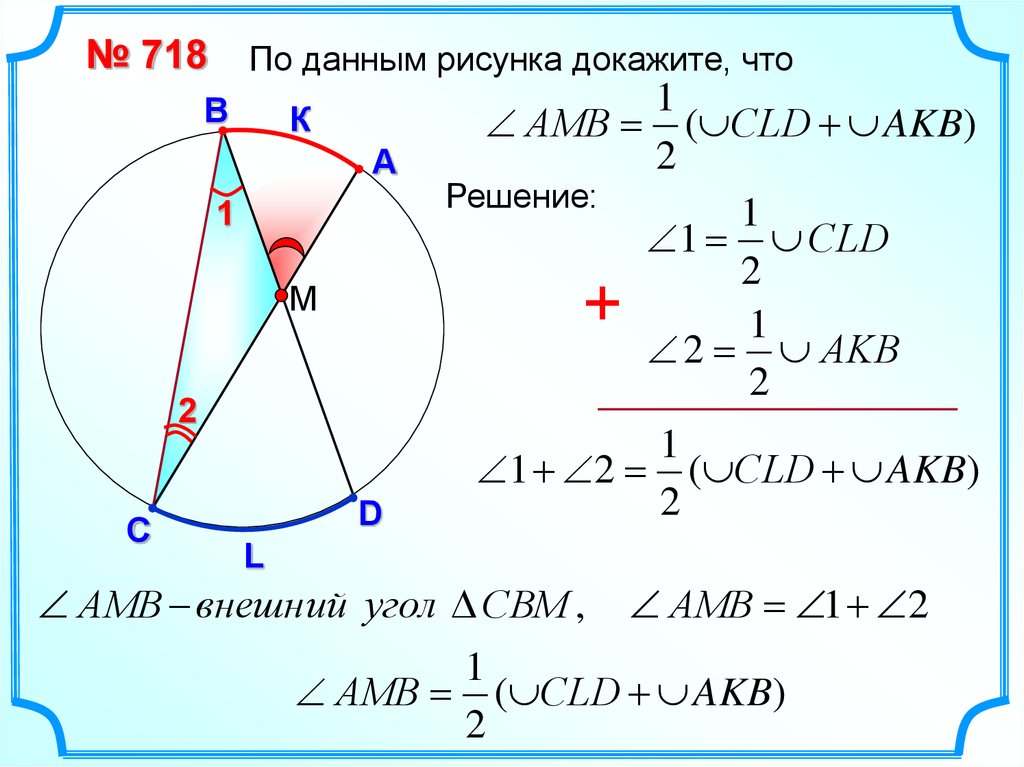
№ 718По данным рисунка докажите, что
В
К
А
1
+
М
2
С
1
АМВ ( СLD AKB)
2
Решение:
1
1 СLD
2
1
2 АKB
2
D
1
1 2 ( СLD AKB)
2
L
АМВ внешний угол СВМ ,
АМВ 1 2
1
АМВ ( СLD AKB)
2
29.
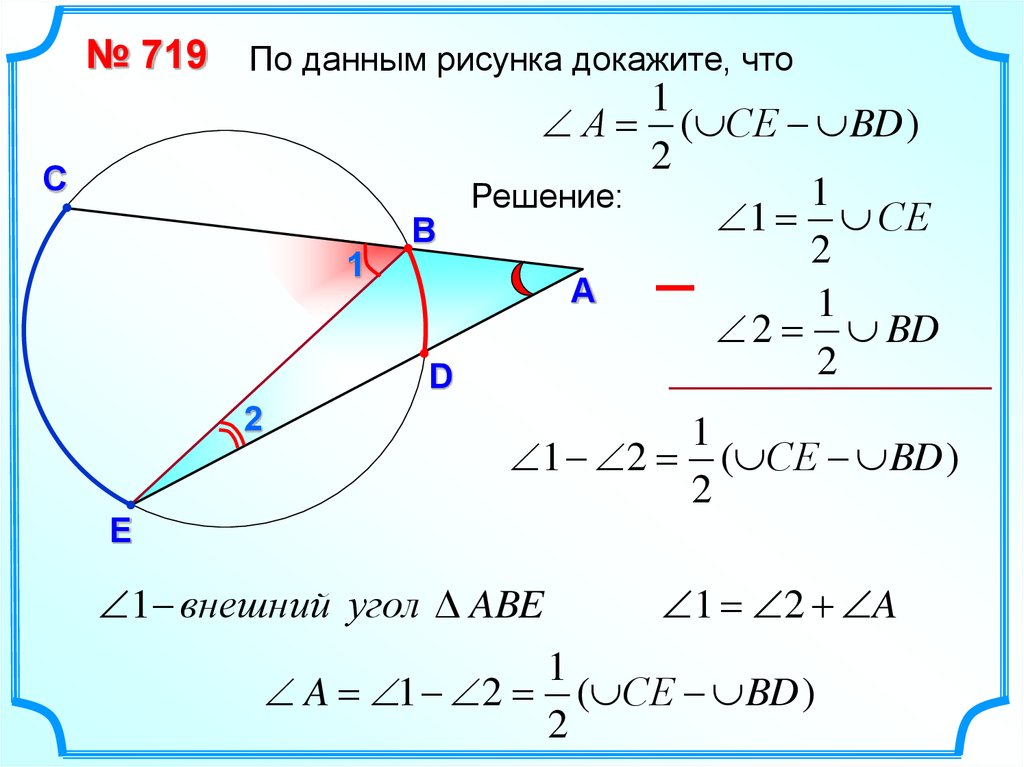
№ 719По данным рисунка докажите, что
С
1
2
1
А ( СЕ BD )
2
1
Решение:
1 СE
В
2
А
1
2 BD
2
D
–
1
1 2 ( СE BD )
2
E
1 внешний угол ABE
1 2 A
1
A 1 2 ( СE BD )
2












 Математика
Математика








