Похожие презентации:
University physics. Forces review of basic concepts
1. University Physics I
ForcesReview of Basic Concepts
2. Vectors and Scalars
All physical quantities (e.g. speed and force) aredescribed by a magnitude and a unit.
VECTORS – also need to have their direction specified
examples: displacement, velocity, acceleration, force.
SCALARS – do not have a direction
examples: distance, speed, mass, work, energy.
3. Representing Vectors
An arrowed straightline is used.
The arrow indicates
the direction and the
length of the line is
proportional to the
magnitude.
Displacement 50m EAST
Displacement 25m at
45o North of East
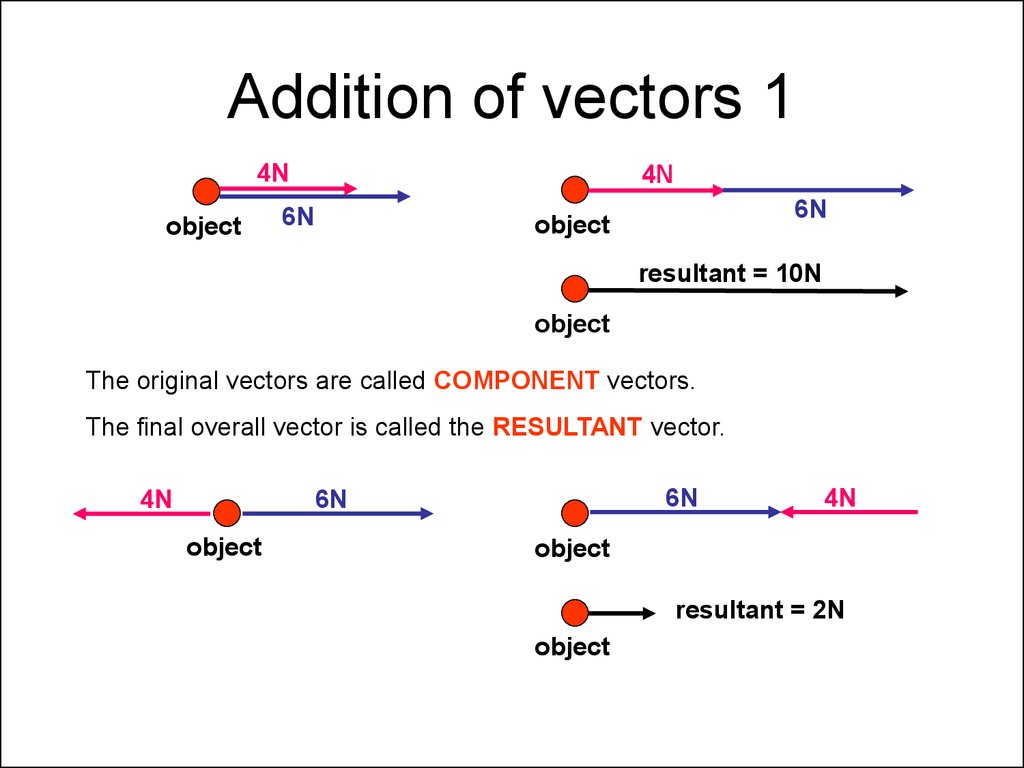
4. Addition of vectors 1
4Nobject
4N
6N
6N
object
resultant = 10N
object
The original vectors are called COMPONENT vectors.
The final overall vector is called the RESULTANT vector.
4N
6N
6N
object
4N
object
resultant = 2N
object
5. Addition of vectors 2
With two vectors acting at anangle to each other:
Draw the first vector.
Draw the second vector with its
tail end on the arrow of the first
vector.
The resultant vector is the line
drawn from the tail of the first
vector to the arrow end of the
second vector.
This method also works with
three or more vectors.
4N
3N
4N
3N
Resultant vector
= 5N
6. Resultant of Two Forces
• force: action of one body on another;characterized by its point of application,
magnitude, line of action, and sense.
• Experimental evidence shows that the
combined effect of two forces may be
represented by a single resultant force.
• The resultant is equivalent to the diagonal of
a parallelogram which contains the two
forces in adjacent legs.
• Force is a vector quantity.
2-6
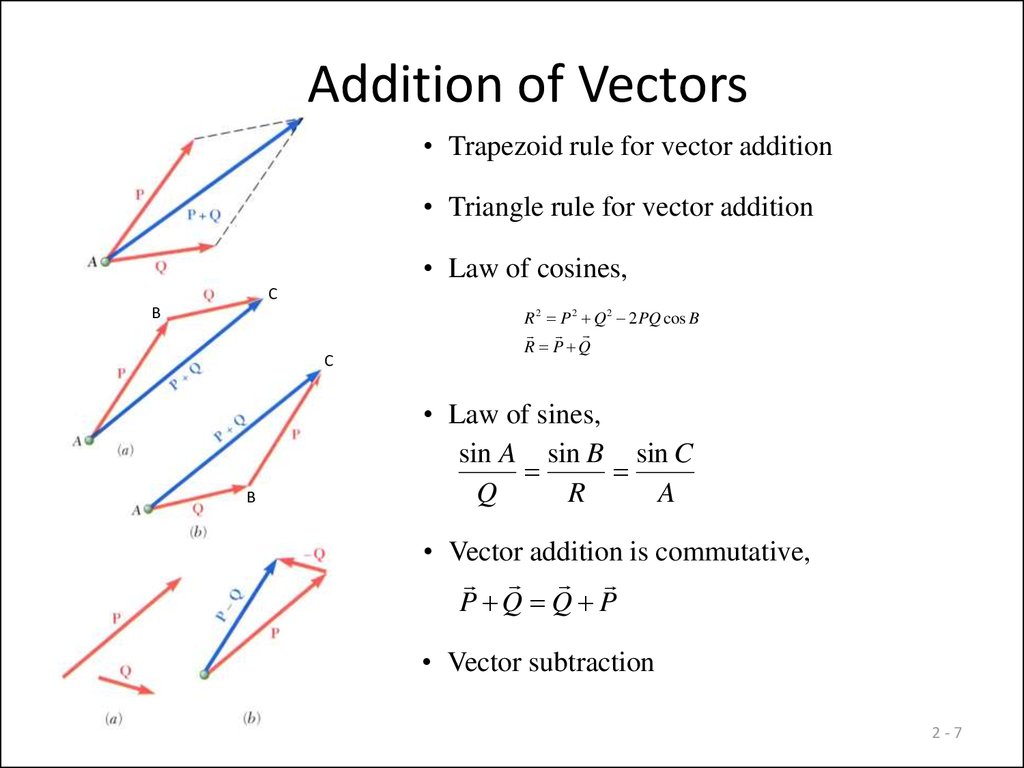
7. Addition of Vectors
• Trapezoid rule for vector addition• Triangle rule for vector addition
• Law of cosines,
C
B
C
B
R 2 P 2 Q 2 2 PQ cos B
R P Q
• Law of sines,
sin A sin B sin C
Q
R
A
• Vector addition is commutative,
P Q Q P
• Vector subtraction
2-7
8. Addition of Vectors
• Addition of three or more vectors throughrepeated application of the triangle rule
• The polygon rule for the addition of three or
more vectors.
• Vector addition is associative,
P Q S P Q S P Q S
• Multiplication of a vector by a scalar
2-8
9. Resultant of Several Concurrent Forces
• Concurrent forces: set of forces which allpass through the same point.
A set of concurrent forces applied to a
particle may be replaced by a single
resultant force which is the vector sum of the
applied forces.
• Vector force components: two or more force
vectors which, together, have the same effect
as a single force vector.
2-9
10. Rectangular Coordinate System
yx
z
I , j , k : Unit Vectors
11.
Vector Representation:A Ax i Ay j Az k
Magnitude or Absolute Value:
A A Ax2 Ay2 Az2
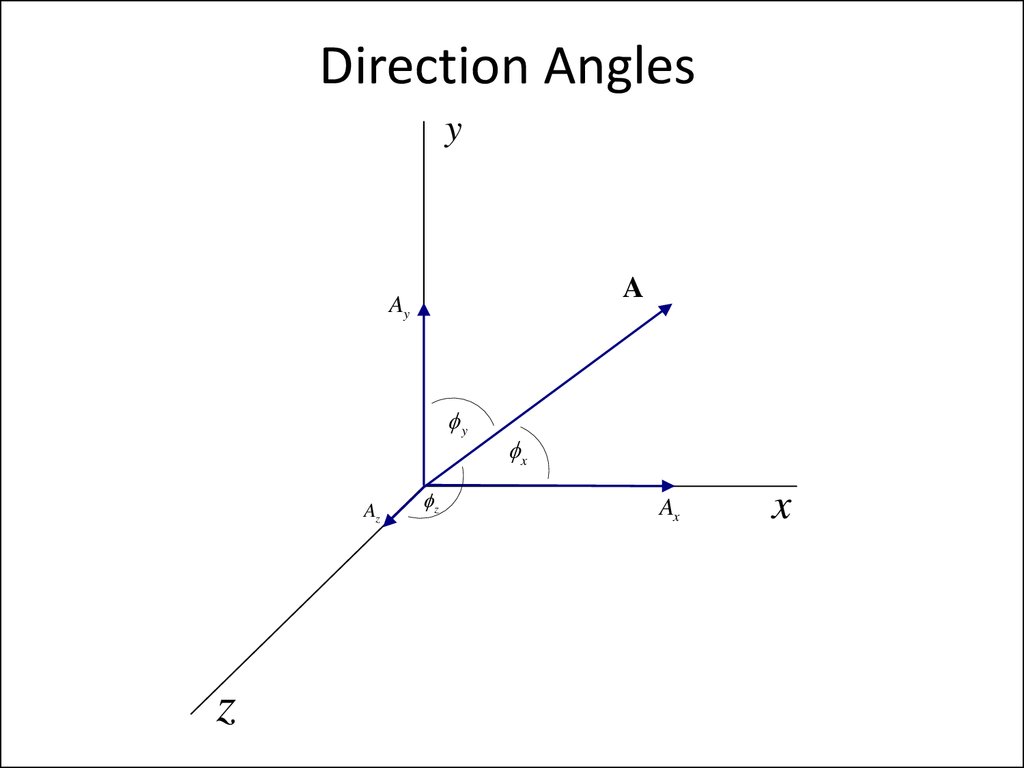
12. Direction Angles
yA
Ay
y
Az
z
z
x
Ax
x
13. Relationships for Direction Angles
Axcos x
A
cos y
Ay
A
Ax
A A A
2
x
2
y
2
z
Ay
A A A
2
x
2
y
Az
cos z
A
2
z
Az
A A A
2
x
2
y
2
z
14. Example 1. A force has x, y, and z components of 3, 4, and –12 N, respectively. Express the force as a vector in rectangular coordinates.
F 3i 4 j 12k15. Determine the magnitude of the force in previous example:
F 3i 4 j 12kF (3) (4) ( 12)
2
13 N
2
2
16. Determine the three direction angles for the force :
Ax 3cos x
0.2308
A 13
x cos 0.2308 76.66 1.338 rad
1
Ay
4
cos y
0.3077
A 13
y cos 0.3077 72.08 1.258 rad
1
17.
Az 12cos z
0.9231
A
13
z cos ( 0.9231) 157.4 2.747 rad
1
18. Vector Operations to be Considered
• Scalar or Dot Product:• Vector or Cross Product:
• Triple Scalar Product:
A•B
AxB
(AxB)•C
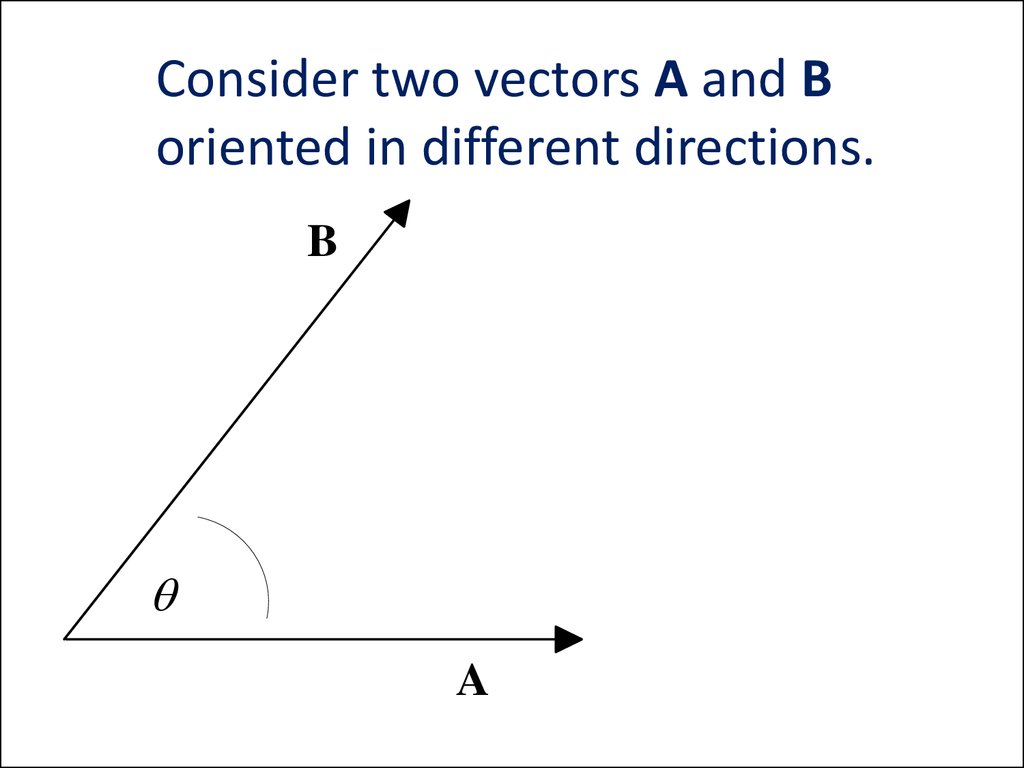
19. Consider two vectors A and B oriented in different directions.
BA
20. Scalar or Dot Product
Definition:A • B AB cos
Computation:
A • B Ax Bx Ay By Az Bz
Represents the Work done by the Force B during the
displacement A for example.
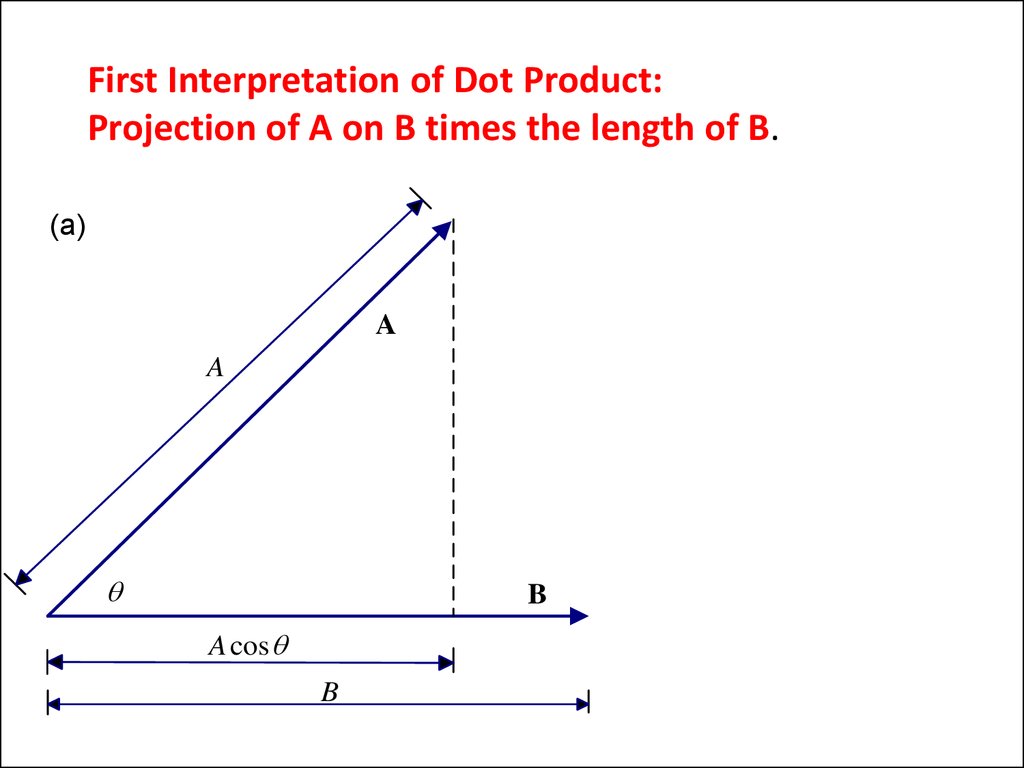
21. First Interpretation of Dot Product: Projection of A on B times the length of B.
(a)A
A
B
A cos
B
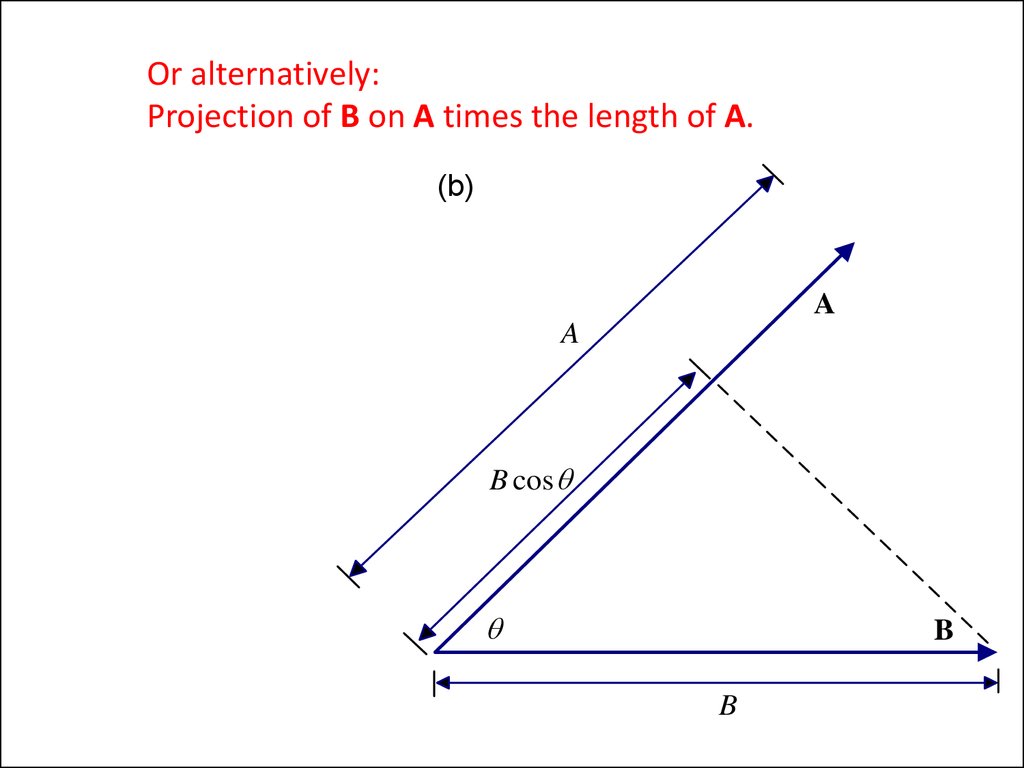
22. Or alternatively: Projection of B on A times the length of A.
(b)A
A
B cos
B
B
23. Some Implications of Dot Product
0The vectors are parallel to each other and
A B AB
90
The vectors are to each other and
A B 0
24. Example : Perform several scalar operations on the following vectors:
A 2i 2 j kB 3i 4 j 12k
A A A A
2
x
2
y
2
z
(2) ( 2) (1) 3
2
2
2
B B B B
2
x
2
y
2
z
(3) (4) (12) 13
2
2
2
25.
A • B Ax Bx Ay By Az Bz(2)(3) (-2)(4) (1)(12) 10
A • B AB cos
A•B
10
10
cos
0.2564
AB
3 13 39
cos 0.2564 75.14 1.311 rad
1
o
26. Vector or Cross Product
The Cross Product of 2 vectors A and B, is a vector Cwhich is perpendicular to both A and B, and whose
Amplitude is (AB sin(θ))
Computation:
Definition:
A × B AB sin un
i
j
k
A × B Ax
Ay
Az
Bx
By
Bz




















 Физика
Физика








