Аналитическая геометрия

1.

Аналитическая геометрия
Аналитическая геометрия изучает геометрические
объекты (линии, поверхности) алгебраическими
(аналитическими) методами. Для этого вводят
понятия уравнения линии или поверхности.
Уравнением линии или поверхности называют
уравнение, которому удовлетворяют координаты
всех ее точек и только они.
Мы будем рассматривать линии и поверхности,
которым соответствуют уравнения первой и второй
степени.
1

2.

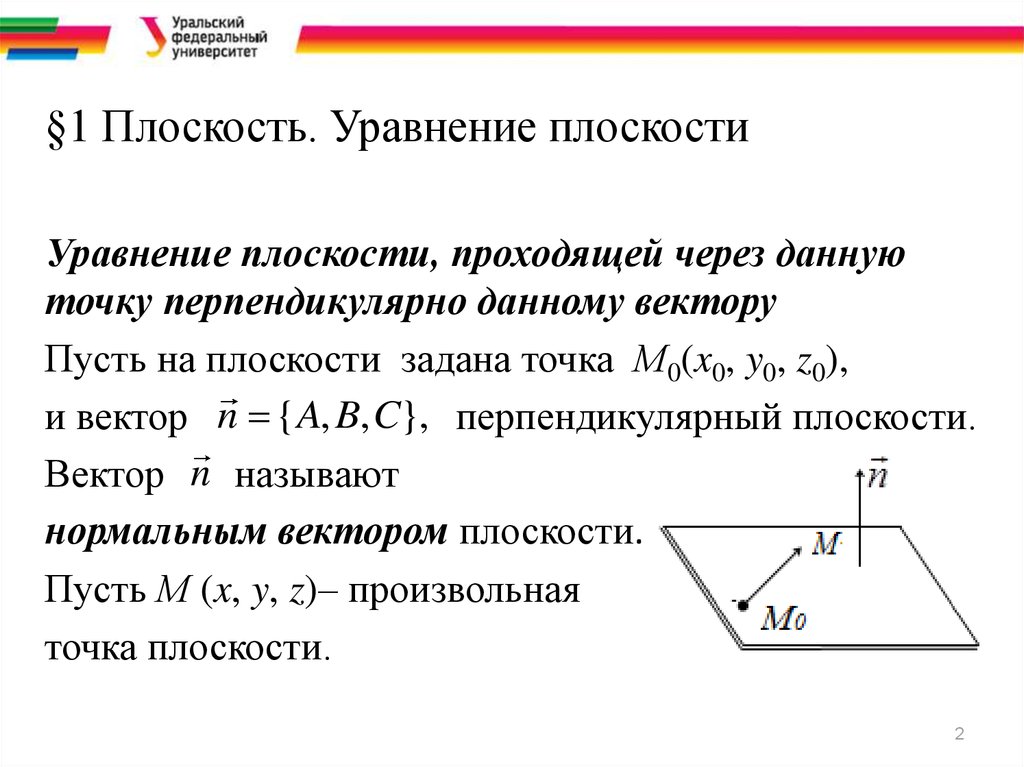
§1 Плоскость. Уравнение плоскости
Уравнение плоскости, проходящей через данную
точку перпендикулярно данному вектору
Пусть на плоскости задана точка М0(x0, y0, z0),
и вектор n { A, B, C}, перпендикулярный плоскости.
Вектор n называют
нормальным вектором плоскости.
Пусть М (x, y, z)– произвольная
точка плоскости.
2

3.

Произвольная точка М принадлежит плоскости тогда
и только тогда, когда векторы
перпендикулярны, а значит, их скалярное
произведение равно нулю:
или в координатной форме:
(1)
3

4.

Общее уравнение плоскости
(2)
Коэффициенты A, B, C есть координаты нормального
вектора плоскости.
Уравнение плоскости (2) есть уравнение первой
степени относительно x, y, z.
Справедливо и обратное: всякое уравнение первой
степени определяет плоскость.
4

5.

Неполные уравнения плоскости
Выделим следующие случаи:
• Если в уравнении плоскости отсутствует
переменная х, то плоскость параллельна оси Ох.
• Если в уравнении плоскости отсутствует
переменная y (или z), то плоскость параллельна оси
Oy (или Oz).
• Если в уравнении плоскости отсутствуют две
переменные, например, х и у, то плоскость
параллельна плоскости Оху.
5

6.

Угол между плоскостями. Условие параллельности
и перпендикулярности плоскостей
Угол между плоскостями α1 и α2 определяется как
угол между их нормальными векторами
Поэтому
| n n |
cos
n n
1
1
2
2
6

7.

Плоскости параллельны тогда и только тогда, когда их
нормальные векторы
коллинеарны, т.е.
Плоскости перпендикулярны тогда и только тогда,
когда их нормальные векторы перпендикулярны, т.е.
7

8.

Расстояние от точки до плоскости
Рассмотрим плоскость с уравнением
Ax+By+Cz+D=0 и точку М0(x0, y0, z0).
Опустим из точки М0 на плоскость перпендикуляр
М0O.
Тогда искомое расстояние
8

9.

Пример 1. Найти расстояние от точки M(–1, 4, 5) до
плоскости, проходящей через точку M0(3, –1, 0)
перпендикулярно вектору n {4, 2,1}.
9

10.

Пример 2. Составить уравнение плоскости,
проходящей через три точки A(1, 2, 3); B(0, –2, 1);
C(–4, – 3, 2).
10

11.

§2 Прямая в пространстве
Канонические уравнения прямой
Пусть дана точка M0(х0, y0, z0) ,
лежащая на прямой, и вектор
параллельный прямой
(он называется направляющим вектором прямой).
Каноническими уравнениями прямой в пространстве
называются уравнения вида:
x x
y y
z z
.
m
n
p
0
0
0
11

12.

Параметрические уравнения прямой
Обозначим коэффициент пропорциональности в
полученном соотношении через t, получим
параметрические уравнения прямой в пространстве:
12

13.

Пример . Найти точку Q, симметричную точке
P(2, −5, 7) относительно прямой
13

14.

Общие уравнения прямой в пространстве
Пусть прямая l является линией пересечения двух
непараллельных плоскостей α1 и α2.
Тогда координаты всех точек прямой
удовлетворяют уравнениям первой
и второй плоскости, т.е. системе
уравнений
Система уравнений называется общими уравнениями
прямой в пространстве.
14

15.

Пример. Записать канонические и параметрические
уравнения прямой, заданной общими уравнениями:
15

16.

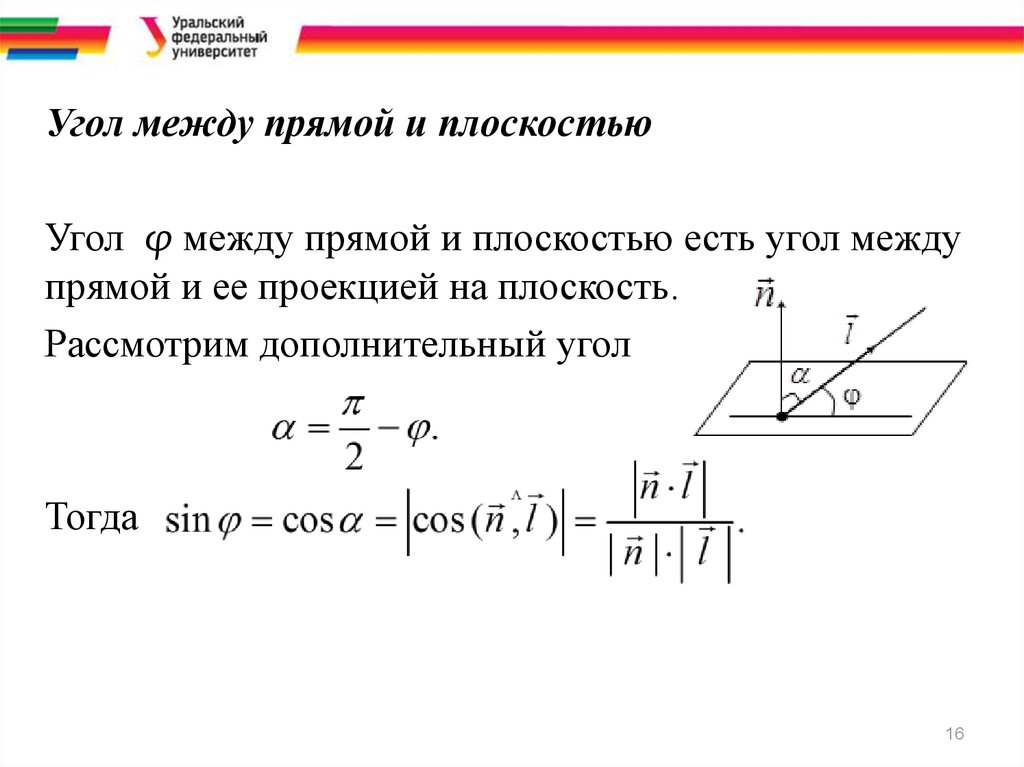
Угол между прямой и плоскостью
Угол φ между прямой и плоскостью есть угол между
прямой и ее проекцией на плоскость.
Рассмотрим дополнительный угол
Тогда
16

17.

Расстояние от точки до прямой в пространстве
Требуется найти расстояние d
от точки М1 до прямой l.
Пусть М0 − известная точка на прямой,
l − направляющий вектор прямой. Рассмотрим
параллелограмм, построенный на векторах M 0 M 1 и l .
С одной стороны, площадь параллелограмма
С другой стороны
17

18.

Поэтому расстояния d от точки М1 до прямой l,
проходящей через точку М0, вычисляется по формуле:
18

19.

§3 Взаимное расположение двух прямых в
пространстве, прямой и плоскости
Пусть
Тогда
−
направляющие векторы прямых ,
M 1 ( x1 , y1 , z1 ), M 2 ( x2 , y2 , z2 ) − точки на прямых.
19

20.

• Прямые параллельны, если их направляющие
векторы коллинеарны, т.е. l1 || l2 или
причем точка
• Прямые совпадают, если их направляющие векторы
коллинеарны и точка одной прямой лежит на
другой прямой:
20

21.

• Прямые пересекаются, если лежат в одной
плоскости и
− компланарны,
тогда
• Прямые скрещивающиеся, если не параллельны и
не лежат в одной плоскости:
и
21

22.

Пример. Определить взаимное расположение прямых
x 3 t 7; Вычислить угол
x 1 y 2 z 5
; y 2 t 2; между ними.
2
3
4
z 2 t 1.
22

23.

Пусть l : x x0 y y 0 z z 0 ;
m
n
p
: Ax By Cz D 0.
• Прямая параллельна плоскости, если векторы
• Прямая лежит в плоскости, если
23

24.

• Прямая пересекает плоскость, если векторы l и n
не ортогональны.
Пример. Выяснить взаимное расположение прямой,
проходящей через точки М1(−1, 0, 1), М2(3, −2, 1) и
плоскости 2x−3y+2z+5=0.
24

25.

25

26.

26

27.

27

28.

28

29.

29