Аналитическая геометрия

1.

8. Аналитическая геометрия
Линия (алгебраическая) на плоскости — ГМТ M (x, y),
координаты которых удовлетворяют уравнению F (x, y) = 0,
где F (x, y) – многочлен степени n.
Поверхность (алгебраическая) — ГМТ M (x, y, z), координаты
которых удовлетворяют уравнению F ( x, y, z) = 0, где F (x, y,
z) – многочлен степени n.
Линия (алгебраическая) в пространстве — пересечение двух
поверхностей:
F1 ( x, y , z ) 0
F2 ( x, y , z ) 0
Уравнение линии или поверхности - нахождение зависимости
между координатами текущей точки.

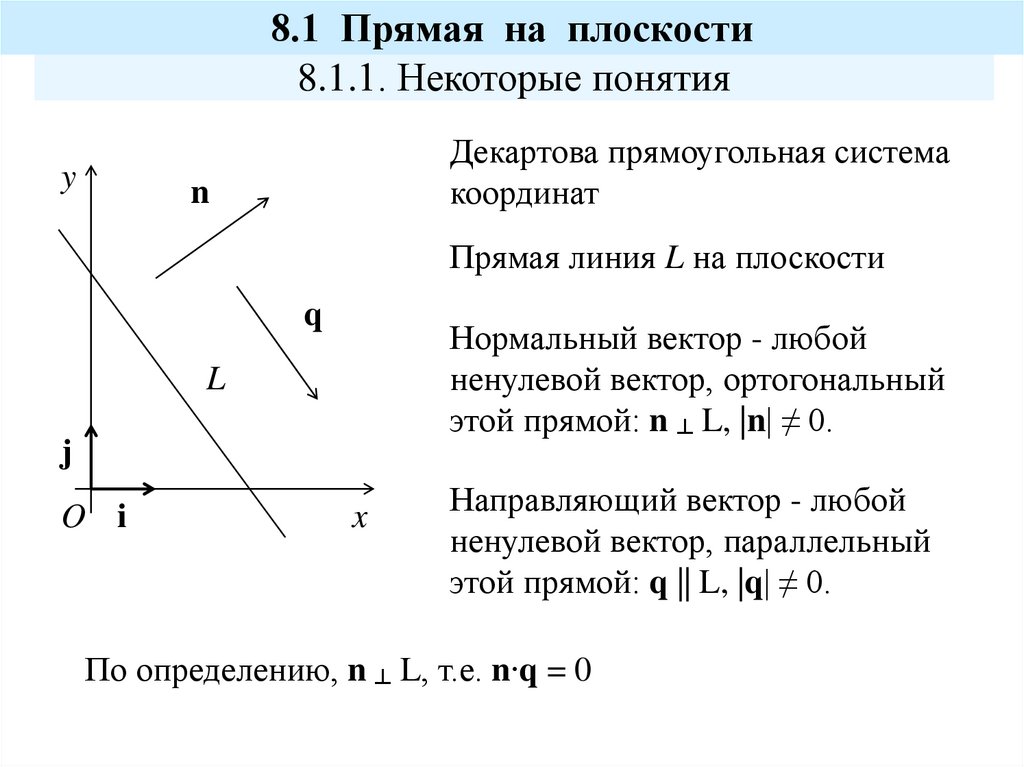
2. 8.1 Прямая на плоскости

8.1.1. Некоторые понятия
y
Декартова прямоугольная система
координат
n
Прямая линия L на плоскости
q
Нормальный вектор - любой
ненулевой вектор, ортогональный
этой прямой: n ┴ L, |n| ≠ 0.
L
j
O i
x
Направляющий вектор - любой
ненулевой вектор, параллельный
этой прямой: q || L, |q| ≠ 0.
По определению, n ┴ L, т.е. n∙q = 0

3.

Пусть n = (A, B) = Ai + Bj, q = (l, m) = li + mj.
n∙q = 0 => Al + Bm = 0
Отсюда, если задан n = (A, B), то q = (B, -A) или q = (-B, A).
И наоборот, если задан q = (l, m), то n = (m, -l) или n = (-m, l).
Проверяем: n∙q = AB-BA = -AB + BA = lm - ml = -lm + ml = 0
Вывод: один из этих векторов на плоскости полностью
задаёт положение прямой, и по нему можно найти другой
вектор.

4.

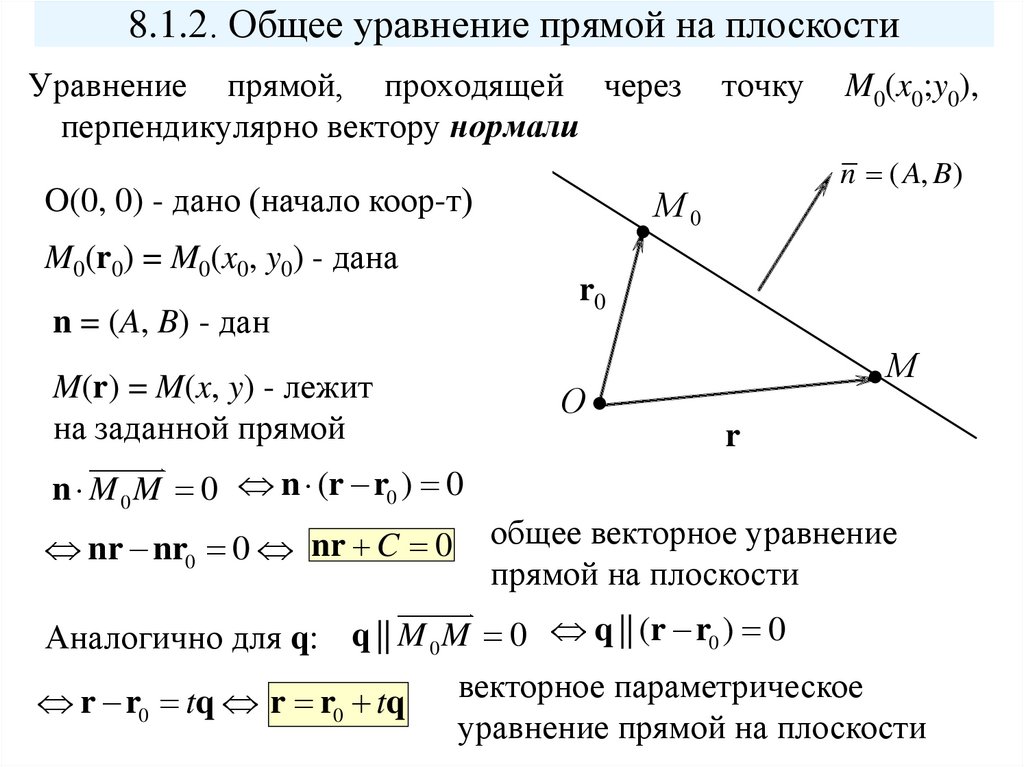
8.1.2. Общее уравнение прямой на плоскости
Уравнение прямой, проходящей через
перпендикулярно вектору нормали
O(0, 0) - дано (начало коор-т)
M0(r0) = M0(x0, y0) - дана
n = (A, B) - дан
M(r) = M(x, y) - лежит
на заданной прямой
n M 0 M 0 n (r r0 ) 0
nr nr0 0 nr C 0
точку
M0(x0;y0),
n ( A, B)
M0
r0
M
O
r
общее векторное уравнение
прямой на плоскости
Аналогично для q: q || M 0 M 0 q || (r r0 ) 0
векторное параметрическое
r r0 tq r r0 tq
уравнение прямой на плоскости

5.

То же самое для координат:
n M 0M 0
( A, B) ( x x0 , y y0 ) 0
A( x x0 ) B( y y0 ) 0
Ax By C 0
Полное уравнение Ax+By+C = 0 <=> A,B, C — ненулевые.
Частные случаи:
(1) A = 0, B ≠ 0, C ≠ 0 => By + C = 0 или y = y1 - прямая параллельна оси Ox.
(2) B = 0, A ≠ 0, C ≠ 0 => Ax + C = 0 или x = x1 - прямая параллельна оси Oy.
(3) C = 0, A ≠ 0, B ≠ 0 => Ax + By = 0 или y = kx - проходит через начало коор-т.
(4) A = 0, C = 0, B ≠ 0 => y = 0 - прямая совпадает с осью Ox.
(5) B = 0, C = 0, A ≠ 0 => x = 0 - прямая совпадает с осью Oy.
Выводы:
1. Общее уравнение прямой на плоскости - линейное уравнение,
коэффициенты которого - координаты нормального вектора.
2. Если коэффициент при x (y) равен нулю, то прямая параллельна оси Oy
(Ox).
3. Если отсутствует свободный член, то прямая проходит через начало
координат.

6.

8.1.3. Уравнение прямой в отрезках
y
x
Ax By C 0 полное
1
C / A C / B
y
x y
1
a b
(0; b)
(a; 0)
x
a и b – отрезки, отсекаемые прямой на осях Ox и Oy.
Замечание: для частных случаев общего уравнения прямой
уравнения прямой в отрезках не существует.

7.

8.1.4. Нормальное уравнение прямой
Пусть прямая ℓ не проходит через O(0;0).
y
n (cos , cos )
P0
x
O
OP0 – расстояние от начала координат до прямой
cosα·x + cosβ·y + C = 0,
нормальное уравнение прямой
(C = –ρ).

8.

8.1.5. Каноническое уравнение прямой
Уравнение прямой, проходящей через точку M0(x0;y0),
параллельно направляющему вектору
q (l , m)
M0
q
M
O
x x0 y y0
M 0 M || q
l
m
Частные случаи:
(1)
x x0 y y0
, q (0, m)
0
m
- прямая параллельна оси Oy,
уравнение прямой x - x0 = 0;
(2)
x x0 y y0
, q (l , 0)
l
0
- прямая параллельна оси Ox,
уравнение прямой y - y0 = 0.

9.

8.1.6. Уравнение прямой, проходящей через две точки
q M 1M 2 ( x2 x1 , y2 y1 )
M1
M2
Подставляем в каноническое
уравнение:
x x0 y y0
l
m
x x1
y y1
x2 x1 y2 y1
Следствие: условие того, что три точки M1(x1, y1), M2(x2, y2),
M3(x3, y3) лежат на одной прямой:
x3 x1 y3 y1
x2 x1 y2 y1

10.

8.1.7. Параметрические уравнения прямой
Векторное параметрическое уравнение прямой: r r0 tq
Найдём это уравнение в декартовых координатах из
канонического уравнения прямой:
x x0 y y0
l
m
x x0 t l
y y0 t m
x x0 y y0
t
l
m
x t l x0
y t m y0

11.

8.1.8. Уравнение прямой с угловым коэффициентом
x x0 y y0
m
y y0 x x0
l
m
l
y
m
m
x y0 x0 y kx b
l
l
m
k tg
l
y
q
m
L
φ
O
l
x
b
Частные случаи:
(1) если φ = 0, то к = 0 и y = b, т.е. прямая параллельна оси Ox;
(2) если φ < π/2, то к = tg φ > 0;
(3) если φ > π/2, то к = tg φ < 0;
(4) если φ = π/2, то к = tg φ не существует, уравнения прямой с
угловым коэффициентом – тоже;
(5) если b = 0, то y = kx, и прямая проходит через начало коор-т.

12. 8.1.9. Взаимное расположение прямых на плоскости

либо параллельны,
либо пересекаются.
ℓ1: A1x + B1y + C1 = 0
ℓ2: A2x + B2y + C2 = 0
n1 = (A1, B1), q1 = (l1, m1), k1
n2 = (A2, B2), q2 = (l2, m2), k2
Прямые параллельны, если:
(1) n1 || n 2
A1 B1
;
A2 B2
(2) q1 || q 2
l1 m1
;
l2 m2
1
n1
n2
1
2
(3) k1 = k2.
1
2
2
x

13.

Прямые перпендикулярны, если:
(1) n1 n 2 n1 n 2 0 A1 A2 B1B2 0;
(2) q1 q 2 l1l2 m1m2 0;
(3) k1k2 = -1.
Угол между прямыми:
n1n 2
(1) cos
n1 n 2
(2) cos
A B
2
1
2
1
A B
2
2
2
2
q1q 2
l1l2 m1m2
;
q1 q 2
l12 m12 l22 m22
1
n2
2
A1 A2 B1 B2
n1
;
k1 k2
(3) tg
.
1 k1k2

14. 8.1.10. Расстояние от точки до прямой

Пусть прямая ℓ задана уравнением Ax + By + C = 0 ,
M0(x0;y0) – точка, не на прямой ℓ.
Найти расстояние от т.M0 до прямой ℓ .
M0
расстояние от т. M0 до прямой ℓ —
модуль скалярной проекции
вектора M0M1 на нормаль прямой ℓ:
n
d
M1
n M 1M 0 ( A, B) ( x0 x1 , y0 y1 )
d прn M 1M 0
n
A2 B 2
C
Ax0 Ax1 By 0 By1
| Ax0 By 0 Ax1 By1 |
2
2
A B
A2 B 2
| Ax0 By 0 C |
d
A2 B 2

15.

8.1.11. Уравнение прямой, проходящей через точку
Дано: фиксированная точка прямой M0(x0, y0).
1. Пусть задан вектор нормали n = (A, B). Найти уравнение
прямой, проходящей через М0 и перпендикулярной n.
Общее уравнение прямой: Ax + By + C = 0
М0 лежит на прямой => Ax0 + By0 + C = 0
=> A(x – x0) + B(y – y0) = 0
2. Пусть задан угловой коэффициент k. Найти уравнение
прямой, проходящей через М0, с коэффициентом k.
y = kx + b
=> y0 = kx0 + b
=> y – y0 = k(x – x0)

16.

Пример на нахождение других уравнений прямой
Дано: общее уравнение 3x - 4y - 12 = 0
Найти: другие уравнения этой прямой
Из уравнения: A = 3; B = -4 => n = (3; -4) => q = (4; 3)
3
Выражаем y: 4 y 3x 12 y x 3 - уравнение прямой с
4
угловым коэффициентом
x y
Делим на сво3 x 4 y 12
1 - уравнение прямой
бодный член:
4 3
в отрезках
x x0 y y0
x 4 y x 4, y 0
Каноническое
0
0
m
4
3
уравнение прямой: l
x 4t 4
Параметрическое x 4 y
t
уравнение прямой: 4
3
y 3t
или:
x lt x0 4t 4
y mt y0 3t

17.

Пример на нахождение угла между прямыми
Дано: прямая 2x + y - 1 = 0
Найти: угол между прямой и прямой с q2 = (1; 3), проходящей
через точку (3; 2).
n1 = (2; 1)
q2 = (1; 3) => n2 = (3; -1)
n1 n 2
2 3 1 ( 1)
5
2
cos
n1 n 2
2
4 1 9 1
50
2
arccos
2
4

18.

Ещё пример на нахождение угла между прямыми
Дано: прямая L1 отсекает на координатных осях отрезки (2; -3),
а прямая L2 проходит через точки A(-1; 2) и B(1; -3).
Найти: угол между прямыми.
x y
L1 :
1 3x 2 y 6 0 n1 ( 3; 2)
2 3
x 1
y 2
L2 :
1 5 x 2 y 1 0 n2 (5; 2)
1 ( 1) 3 2
cos
n1 n2
3 5 2 2
11
11
n1 n2
9 4 25 4
13 29
377
11
arccos
377

19.

Пример на нахождение уравнения прямой, проходящей через точку
Дано: точка M(4; -1), прямая 4x + 3y + 5 = 0
Найти: общее уравнение прямой, проходящей через M и
перпендикулярной данной.
n1 = (4; 3)
n2 = (3; -4) (по условию)
Уравнение прямой, проходящей через
данную точку перпендикулярно n2:
=> 3(x - 4) - 4 (y+1) = 0
A(x – x0) + B(y – y0) = 0
=> 3x - 4y - 16 = 0

20.

Пример на нахождение высоты в треугольнике
Дано: треугольник ABC, где A(2; 1), B(1; -1), C(3; 5).
Найти: длину высоты, опущенной из A.
Другими словами, нужно найти расстояние от A до прямой,
проходящей через B и C.
Уравнение прямой,
проходящей через B и C:
x x1
y y1
x2 x1 y2 y1
x 1 y 1
3 1 5 1
x 1 y 1
x 1 y 1
3x 3 y 1 3x y 4 0
2
6
1
3
d
| Ax0 By 0 C |
A2 B 2
h
3xA y A 4
x y
2
A
2
A
3 2 1 4
9 1
1
10