Похожие презентации:
Множества. Подмножество
1. МНОЖЕСТВА
Множество – это совокупность объектов произвольной природы, определенная
некоторым правилом.
если a является элементом множества A, то пишут
если же нет, то
Примеры:
Числовое множество
Множество участников олимпиады
по информатике
Множество летающих
крокодилов
2. Подмножество
• Множество А являетсяподмножеством множества В,
если все элементы А
принадлежат В.
• Запись: А В
• А={1, 3, 5} В={1,2,3,4,5,6,7,8,9};
• Можно сказать также, что в А нет такого элемента,
который не принадлежал бы множеству В.
3. Пустое множество – МНОЖЕСТВО, В КОТОРОМ НЕТ ЭЛЕМЕНТОВ
4. ПАРАДОКС БРАДОБРЕЯ
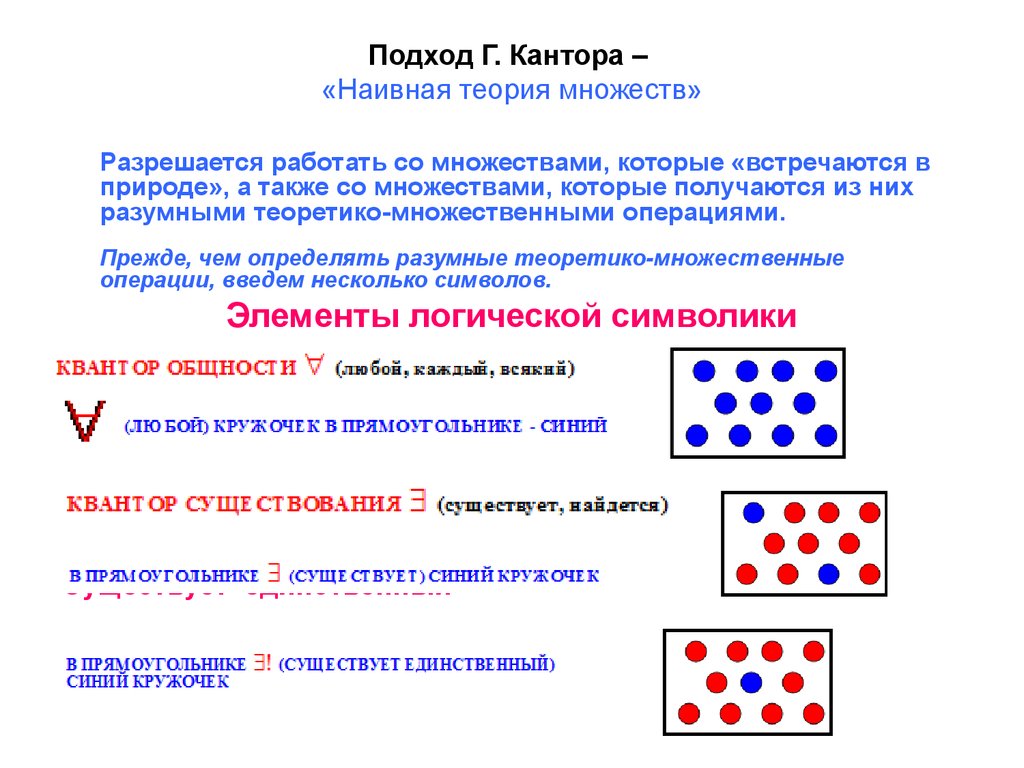
5. Подход Г. Кантора – «Наивная теория множеств»
Разрешается работать со множествами, которые «встречаются вприроде», а также со множествами, которые получаются из них
разумными теоретико-множественными операциями.
Прежде, чем определять разумные теоретико-множественные
операции, введем несколько символов.
Элементы логической символики
Существует единственный
6. Импликация «СЛЕДОВАТЕЛЬНО»
7.
8.
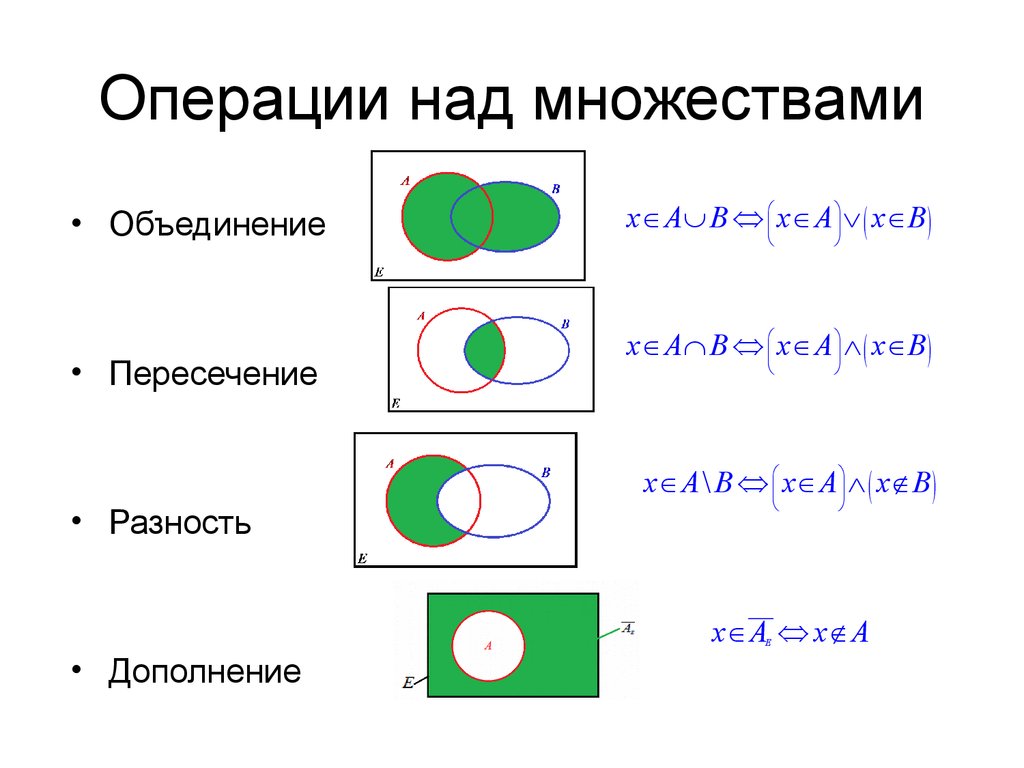
9. Операции над множествами
• Объединение• Пересечение
• Разность
x Î AÈ B Û æç x Î Aö÷ Ú ( x ÎB )
è
ø
x Î AÇ B Û æç x Î Aö÷ Ù ( x ÎB )
è
ø
x Î A \ B Û æç xÎ Aö÷ Ù ( xÏ B )
è
ø
xÎ A Û xÏ A
E
• Дополнение
10.
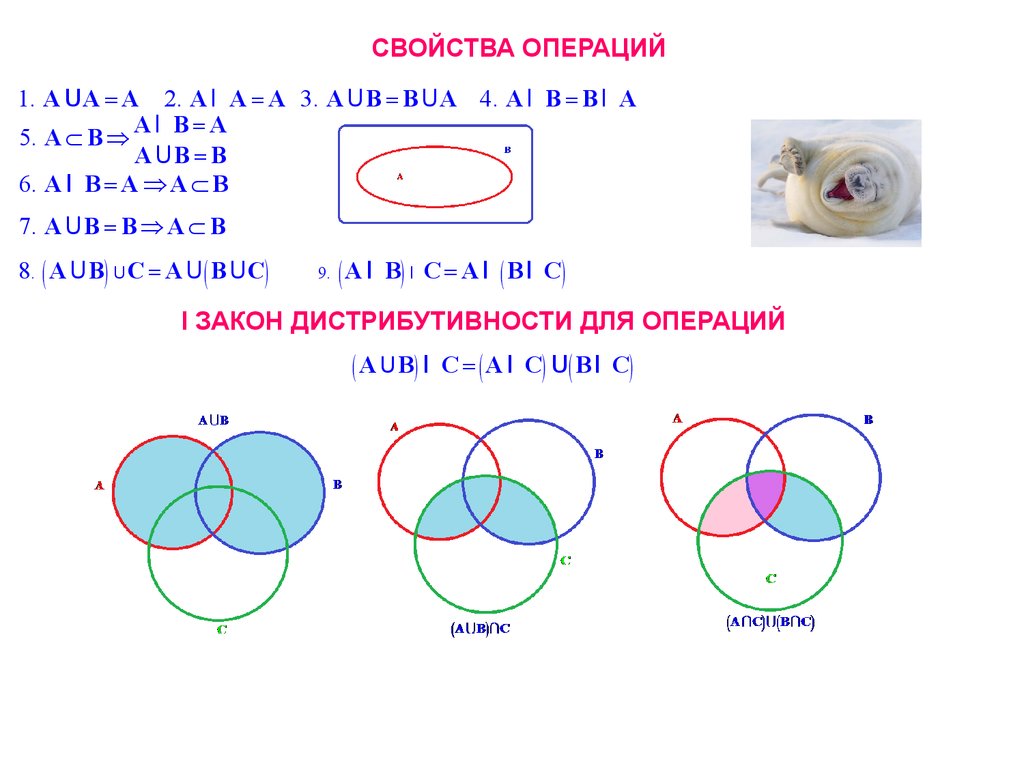
СВОЙСТВА ОПЕРАЦИЙ1. A U A = A 2. A I A = A 3. A UB = B U A 4. A I B = B I A
AI B= A
5. A Ì B Þ
A UB = B
6. A I B = A Þ A Ì B
7. A UB = B Þ A Ì B
8. ( A U B ) U C = A U ( B U C )
9.
( A I B ) I C = A I ( B I C)
I ЗАКОН ДИСТРИБУТИВНОСТИ ДЛЯ ОПЕРАЦИЙ
( A UB) I
C = ( A I C ) U ( B I C)
11.
II ЗАКОН ДИСТРИБУТИВНОСТИ ДЛЯ ОПЕРАЦИЙ( A I B ) U C = ( A U C) I ( B U C )
12.
КОЕ-ЧТО ИЗ СВОЙСТВ ДОПОЛНЕНИЙAÈ B = AE Ç BE
AÇ B = AE U BE
Задача. докажите эти свойства аналитически.
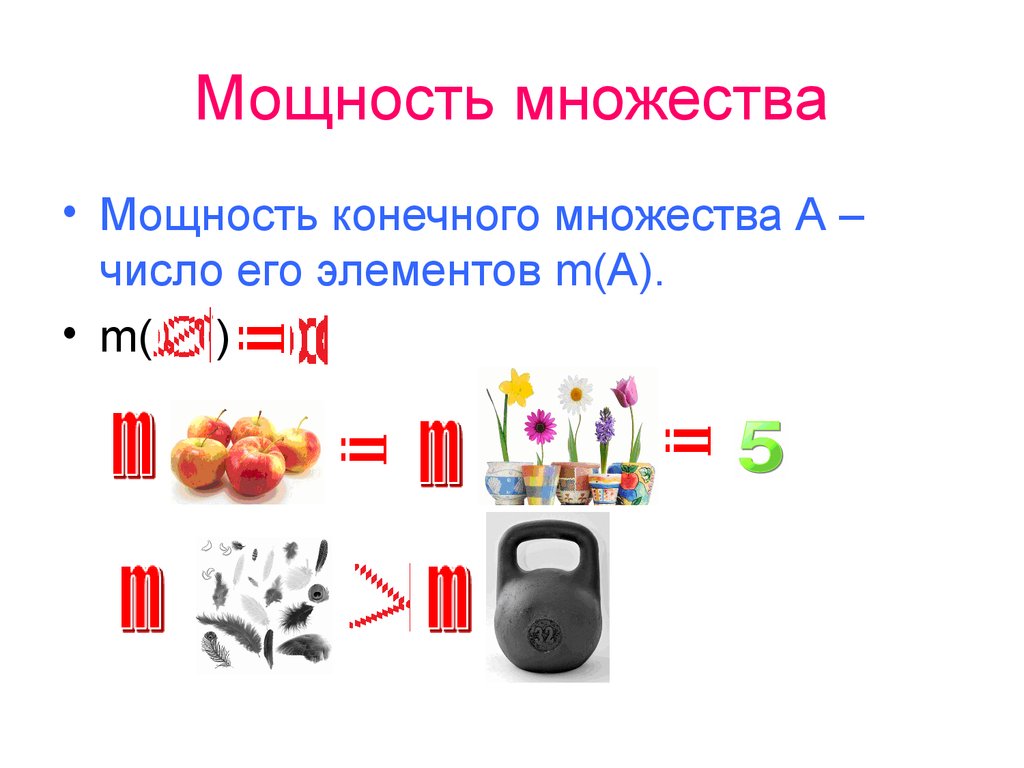
13. Мощность множества
• Мощность конечного множества А –число его элементов m(А).
• m( )
14.
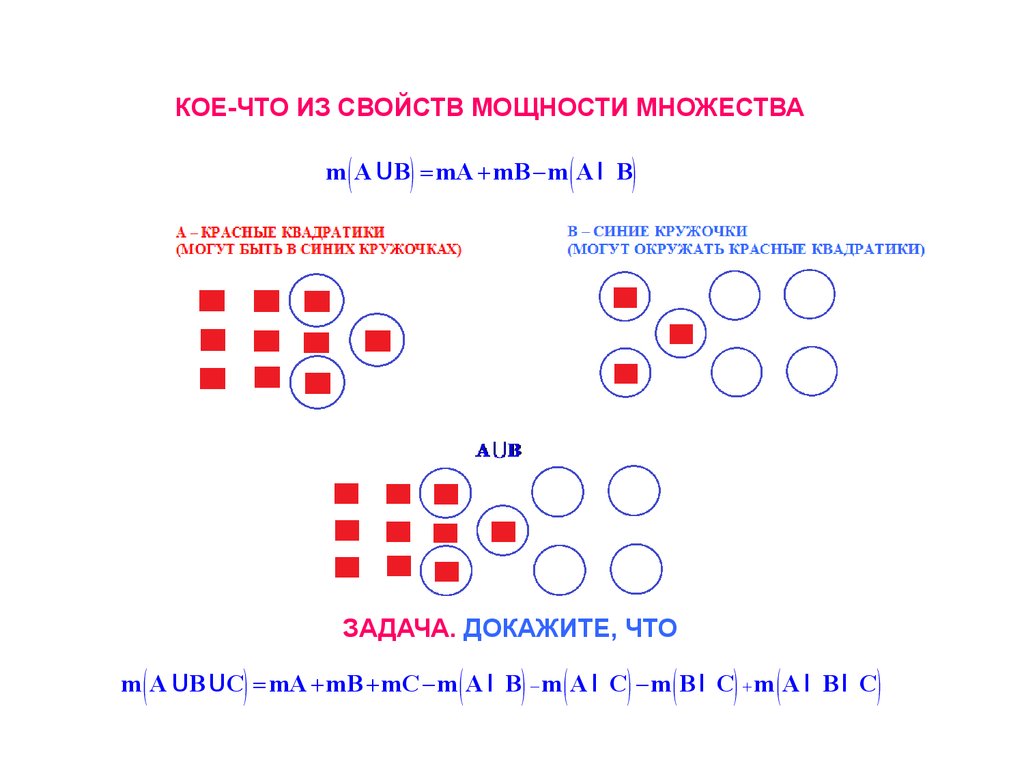
КОЕ-ЧТО ИЗ СВОЙСТВ МОЩНОСТИ МНОЖЕСТВА(
)
(
m A UB = mA + mB - m A I B
)
ЗАДАЧА. ДОКАЖИТЕ, ЧТО
(
)
(
) (
)
(
) (
m A UB UC = mA + mB + mC - m A I B - m A I C - m B I C + m A I B I C
)
15.
А МОЖНО СРАВНИВАТЬ МОЩНОСТИБЕСКОНЕЧНЫХ МНОЖЕСТВ?
Можно. Например, мощность множества целых чисел
меньше мощности множества действительных чисел.
Ну это даже мне понятно!:-)
А вот на отрезке
точек столько же, как и в квадрате.
Но это тема для отдельной беседы.










 Математика
Математика








