Похожие презентации:
Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 14
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 144. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И
ВЫПУКЛЫМИ МНОЖЕСТВАМИ
2.
4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИФУНКЦИЯМИ И
ВЫПУКЛЫМИ МНОЖЕСТВАМИ
4.1. Надграфик выпуклой функции.
4.2. Множество Лебега выпуклой функции.
4.3. Опорная функция подмножества пространства
Rn .
4.4. Опорные функции выпуклых оболочек подмножеств
пространства
Rn .
3.
4.1. Надграфик выпуклой функции.Между выпуклыми функциями и выпуклыми
множествами существует определенная связь.
I
z2
Определение 1.
Надграфиком (эпиграфом) функции
I,
n
U
Ì
R
, называется множество
z1
ìæ u ö
ü
u
n +1
epi I = í ç ÷ Î R u Î U , g ³ I (u ) ý .
a
b
îèg ø
þ 1
На рисунке закрашенное множество является надграфиком функции I : [ a, b ] ® R .
определенной на множестве
Теорема 1. Для того чтобы функция
I,
определенная на выпуклом множестве
U Ì R n , была выпуклой, необходимо и достаточно, чтобы ее надграфик был
выпуклым множеством.
Доказательство. Необходимость. Пусть функция
æ u1 ö
æ u2 ö
ç
÷
z
=
,
z
=
точек 1 ç ÷ 2 çç ÷÷ , z1 , z 2 Î epi I
èg 1 ø
èg 2 ø
I-
выпуклая. Для любых двух
составим их выпуклую комбинацию
æ a u1 + ( 1 - a ) u2 ö æ ua ö
za = a z1 + ( 1 - a ) z2 = ç ag + 1 - a g ÷ = ç g ÷ , a Î [ 0,1] .
) 2ø è aø
è 1 (
4.
Из выпуклости множестваа из выпуклости функции
I
U
следует, что
вытекает неравенство
£g 1
ua = a u1 + ( 1 - a ) u2 Î U ,
£g 2
I ( ua ) = I ( a u1 + ( 1 - a ) u2 ) £ a I (u1 )+ ( 1 - a ) I (u2 ) £ ag 1 + ( 1 - a ) g 2 = g a
которое влечет за собой включение
Необходимость доказана.
æ ua ö
za = ç ÷ Î epi I . = ìí æç u ö÷ Î R n +1 u Î U , g ³ I (u ) üý
îèg ø
þ
èga ø
Достаточность. Пусть множество
Тогда
epi I выпукло в R n +1
и
u1 , u2 Î U , a Î [ 0,1] .
I
æ u1 ö
æ u2 ö
z1 = ç
÷ Î epi I , z2 = ç
÷ Î epi I Þ
I
u
I
u
è ( 1) ø
è ( 2) ø
æ a u1 + ( 1 - a ) u2
ö
a z1 + ( 1 - a ) z2 = ç
÷ Î epi I ,
è a I ( u1 ) + ( 1 - a ) I ( u2 ) ø
Отсюда в силу определения множества
epi I
следует
I ( a u1 + ( 1 - a ) u2 ) £ a I (u1 ) + ( 1 - a ) I (u2 )
что и означает выпуклость функции
I.
Теорема доказана.
z1
a
u1
za
z2
u
ua u2
b
5.
Упражнение.которых
Построить множество точек на плоскости, координаты
( x, y )
удовлетворяют системе неравенств
2
ì
y
x
+ 4 x - 3 ³ 0,
ï
í
2
x
+
y
- y - 2 £ 0,
ï
î
и доказать, что это
множество выпуклое.
Решение.
2
ì
ï y - x + 4 x - 3 ³ 0,
Þ
í
2
ï
î- x + y - y - 2 £ 0,
ì x* = 2,
ï
í
1Þ
y* =
ï
î
2
2
ì
y
³
x
- 4 x + 3,
ï
Þ
í
2
ï
îx ³ y - y - 2
ì y ( x* ) = 4 - 8 + 3 = -1,
ï
í
1 1
9;
ï x ( y* ) = - - 2 = î
4 2
4
- x 2 + 4 x - 3 = 0 Þ x1 = 1, x2 = 3,
y 2 - y - 2 = 0 Þ y1 = -1, y2 = 2
ì dy
= 2 x - 4 = 0,
ï
ï dx
Þ
í dx
ï = 2 y -1 = 0
ï
î dy
y
x
6.
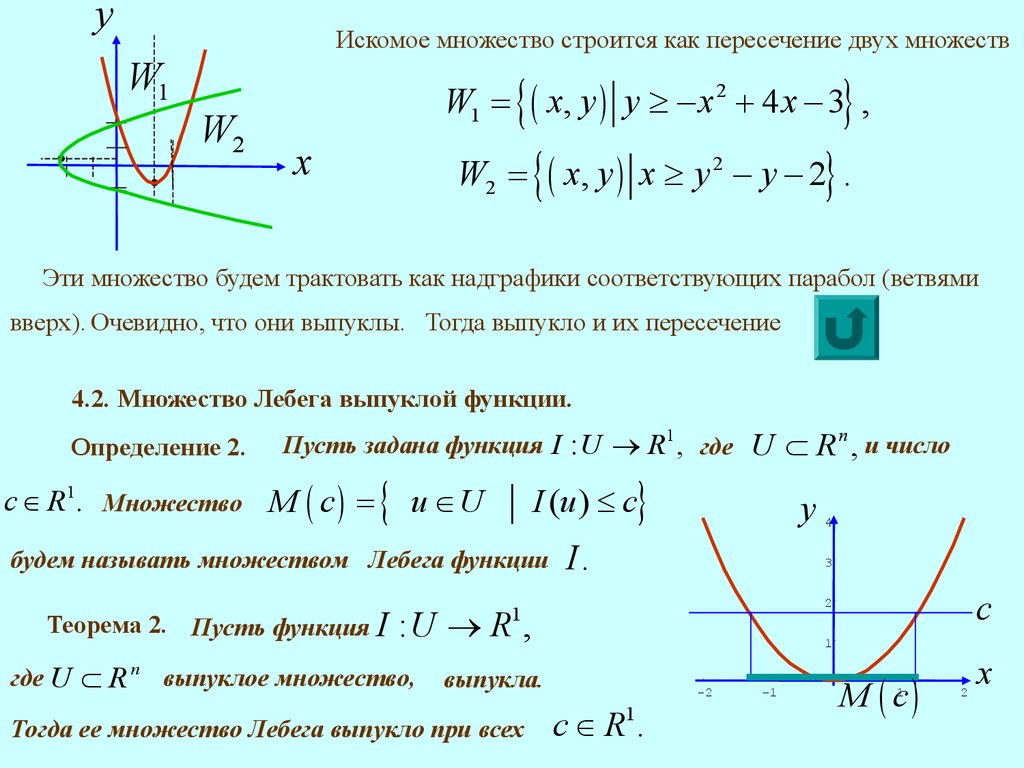
yИскомое множество строится как пересечение двух множеств
W1
W2
x
{ ( x, y ) y ³ - x
= { ( x, y ) x ³ y
}
W1 =
2
+ 4x - 3 ,
W2
2
- y-2 .
}
Эти множество будем трактовать как надграфики соответствующих парабол (ветвями
вверх). Очевидно, что они выпуклы. Тогда выпукло и их пересечение
4.2. Множество Лебега выпуклой функции.
Определение 2.
Пусть задана функция I : U ® R1 , где
с Î R1. Множество М ( c ) =
{
I (u ) £ c}
u ÎU
будем называть множеством Лебега функции
Теорема 2. Пусть функция I
U Ì R n , и число
y
I.
3
1
1
выпукла.
Тогда ее множество Лебега выпукло при всех
c
2
:U ® R ,
где U Ì R n выпуклое множество,
4
-2
сÎR .
1
-1
M ( c)
1
2
x
7.
Доказательство. Для любыхфункции
I
u1 , u2 Î M ( c )
a Î [ 0,1]
и
из выпуклости
и определения множества Лебега выводим
£c
£c
I ( a u1 + ( 1 - a ) u2 ) £ a I (u1 )+ ( 1 - a ) I (u2 ) £ a c + ( 1 - a ) c = c.
Таким образом,
a u1 + ( 1 - a ) u2 Î M ( c ) .
Теорема доказана.
Заметим, что обратное утверждение неверно: из выпуклости множеств Лебега при всех
c Î R1
вообще говоря, не следует выпуклость функции
I (u ) = u 3 , u Î R 1
(
I.
Например, функция
не является выпуклой, а множества Лебега для нее
M ( c ) = -¥, 3 c ùû
y
выпуклы при всех
0.15
cÎR .
1
0.1
-2
Заметим, что эти множества неограниченны.
M ( c )-0.05
-1
-0.1
-0.15
Выведем условия, когда множества Лебега ограничены
при всех
c Î R1.
Для этого уточним некоторые свойства
неограниченных множеств.
c
0.05
1
2
x
8.
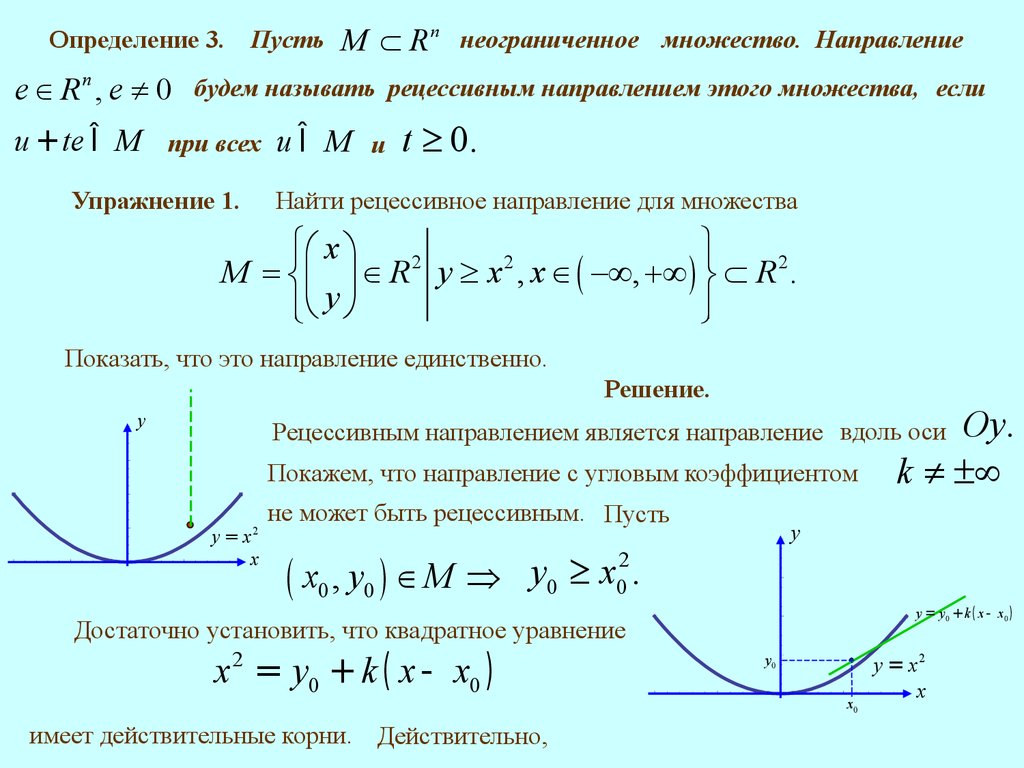
Определение 3. ПустьM Ì R n неограниченное множество. Направление
e Î R n , e ¹ 0 будем называть рецессивным направлением этого множества, если
u + te Î M при всех u Î M и t ³ 0.
Упражнение 1.
Найти рецессивное направление для множества
ìïæ x ö
üï
2
2
M = íç ÷ Î R y ³ x , x Î ( -¥, +¥ ) ý Ì R 2 .
ïîè y ø
ïþ
Показать, что это направление единственно.
Решение.
y
Oy.
k ¹ ±¥
Рецессивным направлением является направление вдоль оси
Покажем, что направление с угловым коэффициентом
2
y=x
x
не может быть рецессивным. Пусть
y
2
y
³
x
( x0 , y0 ) Î M Þ 0 0 .
y = y0 + k ( x - x0 )
Достаточно установить, что квадратное уравнение
x = y0 + k ( x - x0 )
2
имеет действительные корни. Действительно,
y0
x0
y = x2
x
9.
x 2 = y0 + k ( x - x0 ) Þ x 2 - kx + kx0 - y0 = 0Дискриминант этого уравнения
³ x02
D = k 2 - 4 ( kx0 - y0 ) = k 2 - 4kx0 + 4 y0 ³
k 2 - 4kx0 + 4 x02 =
y
2
= ( k - 2 x0 ) ³ 0 Þ D ³ 0.
Установлено, что для любой точки
( x0 , y0 ) Î M
направление с любым угловым коэффициентом
y = y0 + k ( x - x0
y0
k ¹ ±¥
x0
y = x2
x
пересекает границы множества M . В случае
D = 0 Þ y0 = x0 , k = 2 x0 .
Секущая превращается в касательную и не является рецессивным направлением.
2
Покажем, что не всякое неограниченное множество имеет рецессивные направления.
y
Действительно, множество
y = 2 x2
y = y0 + k ( x - x0 )
y0
x0
y = x2
x
ìïæ x ö
ü
2
2
2ï
M = íç ÷ Î R x £ y £ 2 x ý Ì R n .
ïîè y ø
ïþ
является таковым.
10.
Лемма 1. Замкнутое неограниченное выпуклое множествоимеет хотя бы одно
рецессивное направление.
Доказательство.
последовательности
Пусть
Из неограниченности множества
{ uk } , uk Î M , k = 1, 2,L
M
такой, что
следует существование
uk ® ¥.
u Î M . Полагаем
uk - u
ek =
Þ ek = 1, k = 1, 2,L
uk - u
ek ® e, e = 1.
Не теряя общности, будем считать, что
t³0
Для произвольного
u k ® ¥ для достаточно больших номеров k справедливо
t
неравенство 0 £ a =
£ 1. Тогда из выпуклости множества M для
uk - u
достаточно больших номеров k имеем
в силу
uk - u
uk - u
}
u + t ek
=a Î [ 0,1]
6447448
t
uk - u
( uk - u ) =
= u+
= u +t
uk - u
uk - u
11.
aÎ [ 0,1]( u + tek )
t
=u +
( uk - u ) =
uk - u
®e
= u + a ( uk - u ) = auk +( 1- a ) u Î M Þ u + t ek Î M .
В последнем соотношении перейдем к пределу при
множества
M
получим
u + te Î M , t ³ 0.
Покажем, что для направления
для всех точек
u Î M.
e
включение
k ® ¥.
В силу замкнутости
u + te Î M , t ³ 0
Действительно по доказанному,
выполняется
u + m×e Î M , m³ 0. Пусть
t
число ³ 0 столь велико, что имеет место
Î [ 0,1] . Из выпуклости множества M
u Î M следует включение
M
64444444444Î74444444444
8
Î [ 0,1]
Î [ 0,1]ö
æ
÷
ÎM
ç
ÎM
t
t
t
t
÷
ç
÷
ç
u =
( u + me) +ç1u + te + u - u =
÷
÷
ç
m
m÷
m
m
ç
÷
è
ø
для произвольной точки
12.
tt
t
= u + te + u - u = u + te + ( u - u ) Î M .
m
m
m
Устремляя
из (1) получим
в бесконечность,
u + te Î M .
( 1)
M
с учетом замкнутости множества
в пределе
Лемма доказана.
Теорема 3. Пусть I : R n Þ R 1 выпуклая функция. Для ограниченности множеств
M ( c) Ì R
n
одного числа
при любых значениях
a Î R1 ,
Доказательство.
справедливо включение
c>a
Пусть множество
M ( a) ¹
M ( a) ¹
ограниченно.
ограниченно.
Для
c£a
М ( c ) = { u ÎU I (u ) £ c} Ì { u Î U I (u ) £ a} = М ( a ) .
множество
M ( c)
непрерывности выпуклой функции
выпукло.
достаточно существования хотя бы
при котором множество
Остается рассмотреть лишь случай
значении
c Î R1
I
c > a.
Предположим, что при некотором
неограниченно. Заметим, что в силу
это множество замкнуто, а по теореме 2 и
13.
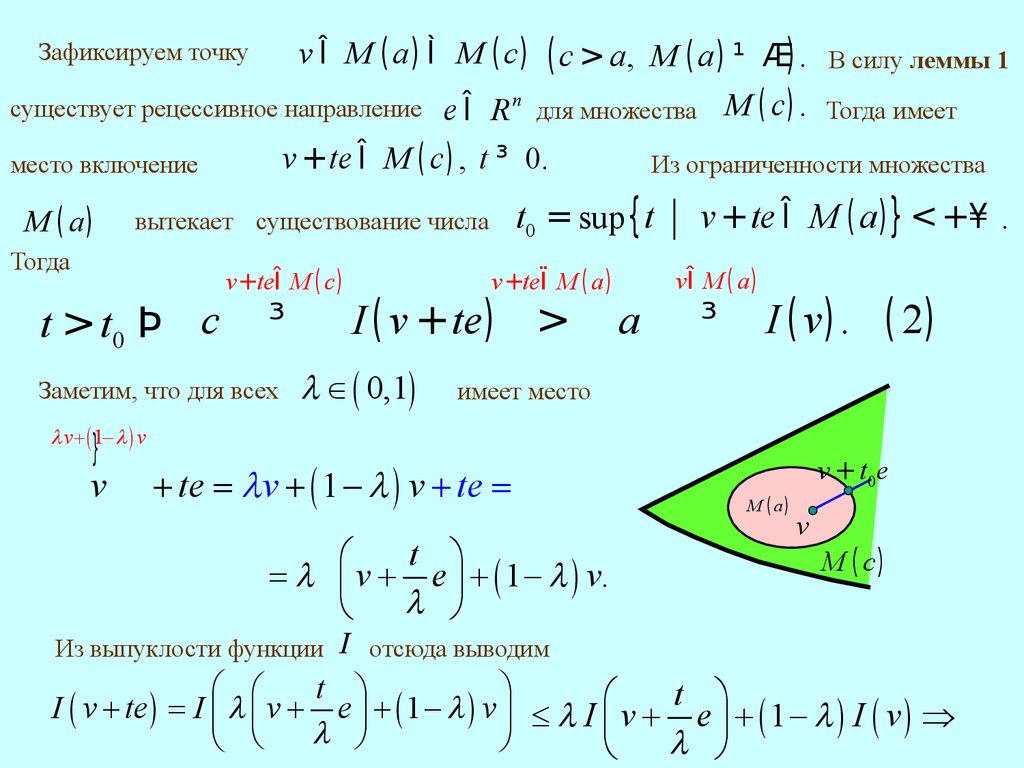
M ( a ) ¹ Æ) . В силу леммы 1существует рецессивное направление e Î R n для множества M ( c ) . Тогда имеет
v Î M ( a) Ì M ( c)
Зафиксируем точку
v + te Î M ( c ) , t ³ 0.
место включение
M ( a)
t > t0 Þ c
v +teÎ M ( c )
³
Заметим, что для всех
v +teÏ M ( a )
I ( v + te) >
l Î ( 0,1)
Из ограниченности множества
t0 = sup { t
вытекает существование числа
Тогда
( c > a,
a
v + te Î M ( a ) } <+¥ .
vÎ M ( a )
³
I ( v ) . ( 2)
имеет место
l v + ( 1- l ) v
}
v
+ te = l v + ( 1 - l ) v + te =
t ö
æ
= l ç v + e ÷ + ( 1 - l ) v.
l ø
è
v + t0 e
M ( a)
v
M ( c)
Из выпуклости функции I отсюда выводим
æ æ
t ö
ö
I ( v + te ) = I ç l ç v + e ÷ + ( 1 - l ) v ÷ £ l I æ v + t e ö + ( 1 - l ) I ( v ) Þ
ç
÷
l ø
è è
ø
l
è
ø
14.
t öæ
I ( v + te ) £ l I ç v + e ÷ + ( 1 - l ) I ( v ) Þ
l ø
è
v + teÏM ( a ) Þ I ( v +te ) > a
æ t ö I
I çv + e÷ ³
è l ø
В (3) устремим
I ( v + te ) > I ( v )
678
( v + te )
vÎM ( a ) Þ I ( v ) £ a
}
( v)
-I
l
lÎ( 0,1)
l ® +0.
( 2)
t ö
æ
l I ç v + e ÷ ³ I ( v + te ) - I ( v ) + l I ( v ) Þ
l ø
è
+ I ( v) .
( 3)
v + t0 e
В силу неравенства (2)
M ( a)
получим
M ( c)
6 4 4 7 4 48
( 3)
t ö
æ
I ( v + te ) - I ( v )
® +¥ Þ I ç v + e ÷ ® +¥.
l ø
l
è
>0
®0
Тогда найдется число
lÎ( 0,1)
l0 > 0,
что
t ö
æ
I çv + e÷ > c
l ø
è
при всех
l Î ( 0, l0 ) .
e (рецессивное направление)
æ t ÷
ö
t
ç
v + e÷
£ c " l Î ( 0,1) .
v + e Î M ( c) Þ I ç
÷
ç
è l ø
l
С другой стороны, по построению вектора
Полученное противоречие доказывает теорему.
v
имеем
15.
Rn .4.3. Опорная функция подмножества пространства
Пусть U Ì R n
компактное множество.
Определение 4. Функция
cU : R n Þ R1 ,
определенная формулой
cU ( v ) = max u, v , v Î R n ,
( 1)
uÎU
называется опорной функцией множества
U.
Максимум в правой части (1) действительно достигается в силу компактности
множества
U и непрерывности скалярного произведения.
Упражнение.
Решение.
Вычислить опорную функцию шара
Максимум в (1) достигается на векторе
ev
ev
cU ( v ) = v,
=
v
v
Упражнение.
O ( 0, e) Ì R n .
2
ev
u = .
v
0
Тогда
v
=e v .
Вычислить опорную функцию квадрата
ìï
üï
æ u1 ö
2
1
2
K ( 0,1) = íu = ç 2 ÷ Î R u £ 1, u £ 1ý .
èu ø
îï
þï
u0
O ( 0, e)
e
u
16.
Решение.cU ( v ) = max u, v =
uÎU
max2
1
(u v
1 1
u £1, u £1
+u v
2 2
= max
( u × v ) + max
( u ×v
1
2
1
u £1
1
2
u £1
æì
-1,
v1 < 0, ö
çï 1
÷ 1
1
= ç í"u Î [ 0,1] , v = 0, ÷ × v +
1
çï
÷
1,
v
>
0
èî
ø
v1
2
)=
)=
v
u0
u
K ( 0,1)
æì
-1,
v 2 < 0, ö
çï 2
÷ 2
2
ç í"u Î [ 0,1] , v = 0, ÷ × v =
2
çï
÷
1,
v
>
0
èî
ø
v2
6 4 47 4 48 6 4 4 7 4 4 8
æ ì-v1 , v1 < 0, ö æ ì-v 2 , v 2 < 0, ö
çï
÷ çï
÷
1
2
= ç í 0, v = 0, ÷ + ç í 0, v = 0, ÷ =
ç ï v1 , v1 > 0 ÷ ç ï v 2 , v 2 > 0 ÷
èî
ø èî
ø
v1 + v 2 .
17.
Свойство 1.Опорная функция является положительно однородной.
Доказательство.
cU ( v )
64
7 48
æ
ö
cU ç l × v ÷ = max u, l × v = l × max u, v = l × cU ( v ) , v Î R n , l ³ 0.
è
ø uÎU
uÎU
n
Свойство 2. Для любых v1 , v 2 Î R справедливо неравенство
³0
³0
cU ( v1 + v2 ) £ cU ( v1 ) + cU ( v2 ) .
Доказательство.
cU ( v1 + v2 )
Свойство 3.
)
U ( v1 )
6 4c7
48 6 4cU7( v248
= max u , v1 + v2 £ max u , v1 + max u, v2 =
uÎU
uÎU
uÎU
cU ( v1 ) + cU ( v2 ) .
Опорная функция является выпуклой функцией.
Доказательство.
По свойству 1 и 2
cU ( a v1 + ( 1 - a ) v2 )
свойство 1
=
свойство 2
£
имеем
cU ( a v1 ) + cU ( ( 1 - a ) v2 )
свойство 1
=
acU ( v1 ) + ( 1 - a ) cU ( v2 ) , v1 , v2 Î R n , a Î [ 0,1] .
18.
nСвойство 4. Пусть U , W Ì R .
Тогда
cU +W ( v ) = cU ( v ) + cW ( v ) .
Доказательство.
cU +W ( v ) = max
u+w
zÎU +W
u + w, v = max éë u, v + w, v ùû =
z , v = uÎmax
uÎU , wÎW
U , wÎW
U ( v)
W ( v)
64c7
48 6 4c7
48
= max u, v + max w, v = cU ( v ) + cW ( v ) .
uÎU
Следствие.
wÎW
Справедливо равенство
cU e ( v ) = c U ( v ) + e v .
Доказательство.
U e = U + O ( 0, e) Þ
cU e ( v ) = cU ( v ) + c O( 0,e) ( v ) = cU ( v ) + e v .
19.
Пример 3.n
Вычислить опорную функцию шара O ( u0 , R ) Ì R .
Решение. В силу представления O ( u 0 , R ) = { u 0 } + O ( 0, R ) и свойства 4 опорной
функции находим
пример1: R v
64 u70 , v48 64
7 48
c O ( u0 , R ) ( v ) = c{ u0 } +O ( 0, R ) ( v ) = c{ u } ( v ) + cO( 0, R ) ( v ) =
0
Пусть
A
квадратная матрица n - го порядка.
Свойство 5. Справедливо равенство
Доказательство. Au
c AU ( v ) = max z , v =
zÎ AU
Следствие 1.
u0 , v + R v .
{
}
Полагаем AU = v = Au u Î U .
c AU ( v ) = cU ( AT v ) .
T
c
A
v ) . ( 2)
(
max Au, v = max u, A v = U
T
uÎ U
uÎ U
Имеет место равенство
c lU ( v ) = cU ( l v ) .
Доказательство. Вытекает из свойства 5 при
c lU ( v ) = c ( l E ) U ( v )
свойство 5
A = l E.
= cU
Действительно,
( ( l E ) v) =
= cU ( ( l E ) v ) = cU ( l v ) .
T
20.
Следствие 2. Опорная функция является положительно однородной по аргументуU Ì Rn ,
т.е.
c lU ( v ) = l cU ( v ) , l ³ 0.
Доказательство. Вытекает из предыдущего следствия и свойства 1. Действительно,
c ³0 ( v )
lU
Свойство 6.
следствие1
=
æ ³0 ö свойство 1
cU ç l v ÷ = lcU ( v ) .
è ø
n
Пусть U , W Ì R , U Ì W -
компактные множества. Тогда
cU ( v ) £ cW ( v ) , v Î "R n .
Доказательство.
U ÌW
w, v = cW ( v ) , "v Î R n .
cU ( v ) = max u, v £ max
wÎW
uÎU


















 Математика
Математика Программирование
Программирование








