Похожие презентации:
Выпуклый анализ. Выпуклые множества. Лекция 9
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 92. ВЫПУКЛЫЕ МНОЖЕСТВА
(ПРОДОЛЖЕНИЕ)
2.
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)2.8. Выпуклые конусы.
2.9. Выпуклые конусы и частичная упорядоченность.
2.10. Многокритериальная оптимизация.
3.
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)2.8. Выпуклые конусы. Выпуклый конус – один из основных объектов изучения
теории экстремальных задач.
Определение 13. Множество
l 0
следует, что
K R n называется конусом,
uÎK
если из
и
l u Î K.
Если множество K выпукло, то конус называется выпуклым, если замкнуто –
замкнутым, если открыто – открытым.
Пример 10. Множества
{
={uÎR
}
K1 = u Î R n a, u = 0 ,
K3
n
K3
}
K 4 = { u Î R n u 0}
K1 , K 2 , K 4
при этом множества
замкнутые,
- открытое.
Здесь и далее запись
u £, , < 0.
}
a, u < 0 ,
являются выпуклыми конусами,
а множество
{
K 2 = u Î R n a, u £ 0 ,
u £, , < 0
означает, что каждая координата вектора
4.
Пример 11. Угол на плоскости раствора, меньшего чемp
является выпуклым
конусом.
Упражнение 1.
конусом.
Доказать, что пересечение выпуклых конусов является выпуклым
Решение.
Ранее было установлено, что пересечение выпуклых множеств выпукло. Докажем,
что пересечение конусов—конус.
n
n
Пусть K R и L R конусы. Полагаем M = K I L. Требуется доказать, что
M - конус. Пусть u Î M и l 0. Имеем
u Î K , u Î L Þ l u Î K , lu Î L Þ lu Î K I L = M
Утверждение доказано.
В частности, пересечение множеств типа
{
}
K 2 = u Î R n a, u £ 0 , называют
многогранным углом.
Приведем некоторые свойства выпуклых конусов.
5.
Теорема 19. Пусть K R nl1 0,L , lm 0,
m
то
l u Î K.
m
Положим l = l i
i =1
Доказательство.
выпуклый конус. Если
u1 ,L , um Î K ,
i i
и будем считать, что
l ¹ 0.
Очевидно,
i =1
li
bi = 0, i = 1,L , m
l
}=l
что
и
li
l
}
bi =
m
i =1
m
li
=
i =1 l
m
Тогда в силу выпуклости множества
m
= bi ui Î K .
i =1
l
i =1
l
K
i
l
= 1.
=
l
справедливо включение
С другой стороны по определению конуса имеем
bi
é
}
} 0
m
ê m æ li
li ui = l × ê ç
i =1
ê i =1 è l
ë
Теорема доказана.
ÎK
48
ù 0 64 7
ù
ö ú } ém
÷ ui ú = l × ê b i ui ú Î K .
ø ú
ë i =1
û
û
}bi
m
æ li
çl
i =1 è
ö
÷ ui =
ø
6.
Приведем важный пример конуса.Упражнение 1. Пусть U Ì R n . Доказать, что множество
conU = { u = av v Î U , a > 0}
(конусная оболочка) является конусом.
Решение.
Пусть
u Î conU .
Тогда
u = a v,
>0
где
a > 0, v Î U .
Для всех
l >0
имеем
ÎU
l u = ( al ) v Î conU .
Таким образом,
conU -
конус.
n
Теорема 20. Если множество U Ì R выпукло, то
conU -
выпуклый конус,
u = av Î int ( conU ) .
Доказательство. Возьмем произвольные точки u1 , u2 Î conU .
u1 = a1v1 , u2 = a2 v2 , v1 , v2 Î U , a1 , a 2 > 0.
причем если
v Î int U , a > 0,
Покажем, что для любых
то
l 1 ³ 0, l 2 ³ 0, l 1 +l 2 = 1 выполнено включение
a1v1
a 2 v2
}
}
l1 u1 + l2 u2 = a1l1v1 + a 2l2 v2 Î conU .
Из условия
Тогда
l 1 ³ 0, l 2 ³ 0, l 1 +l 2 = 1 следует a1l1 + a 2 l2 0.
7.
6 4 7 0 4 86 4 7 0 4 8 ù
é
6 44 7 4 48
ÎU
ÎU ú
ê
a
l
a
l
1
1
2
2
l1u1 + l2u2 = a1l1v1 + a 2 l2 v2 = a1l1 + a 2 l2 × ê
v1 +
v2 ú .
a1l1 + a 2 l2 ú
ê a1l1 + a 2l2
ë
û
Тогда
0
Из выпуклости
U
a1l1
a 2l2
+
= 1 выводим
и равенства
a1l1 + a 2 l2 a1l1 + a 2 l2
a1l1
a 2l2
v1 +
a1l1 + a 2 l2
a1l1 + a 2l2
Выпуклость множества
0
644444>74444
48
v2 Î U Þl 1u1 +l 2u2 Î ( a1l 1 + a2l 2 ) ×
U Ì conU .
conU
доказана.
u = av, a > 0, v Î int U .
e> 0 имеем
Ì7444444
U
6
444444
4
48
a
v
ìï } ü
ï
>0
æÎ int U
ö
ï u ï + O ( 0, ae) = av + O 0, ae =
÷
ç
aU =
{
}
(
)
í ý
a
×
v
+
O
0,
e
Ì
(
)
÷
ç
ïï ïï
÷
ç
è
ø
î þ
Далее пусть
{
>0
}
= u =a w wÎ U Ì
Теорема доказана.
Для малых
{ }
{ u = bw Î
R n b > 0, w Î U } = conU Þ
u Î int ( conU ) .
8.
2.9. Выпуклые конусы и частичная упорядоченность. Используя понятие выпуклогоконуса в пространстве
Rn
отношение «больше».
Определение 14. Пусть
можно ввести частичный порядок его элементов, т.е. ввести
K R
n
v Î R n , если u - v Î K u - v Î int K .
K
æ K ö
случае будем писать u v ç u v ÷ .
è
ø
Когда ясно, о каком конусе идет речь, писать будем просто " ", " ".
не меньше (строго больше)
Принимаем также, что отношение
v£u
v < u .
u Î Rn
- выпуклый конус. Будем говорить, что
u v
Заметим, что если
u v
uÎK
В этом
эквивалентно отношению
u Î int K ,
æ K ö
u 0 ç u 0 ÷.
è
ø
K
то
Перечислим и докажем ряд свойств введенного отношения,
присущие обычным
неравенствам.
n
Теоремы 18. Пусть K R
l1 0,L , lm 0,
m
то
выпуклый конус. Если
l u Î K.
i =1
i i
u1 ,L , um Î K ,
9.
u v следует, что a u a v при a 0.ÎKНеравенство u v означает, что u - v Î K Þ a u - v = a u - a v Î K Þ
1. Из
a u a v.
2. Если
u1 v1
и
u2 v2 ,
то
u1 + u2 v1 + v2 .
Справедливы включения u1 - v1 Î K , u2 - v2 Î K .
ÎK
ÎK
u1 - v1 + u2 - v2 Î K Þ
В силу теоремы 18 имеем
u1 - v1 + u2 - v2 = u1 + u2 - v1 + v2 Î K Þ
u1 + u2 v1 + v2 .
3. Если u v, v w, то u w.
Из включений (u - v ), (v - w) Î K в силу теоремы 18 выводим
ÎK
ÎK
(u - v )+ (v - w) Î K Þ (u - v) + (v - w) = u - w Î K Þ u w.
В случае, когда конус
4.
Если
K
замкнутый, справедливо еще одно свойство
{ uk } ® u0 , { vk } ® v0 , uk vk , k = 1, 2,L
Для всех номеров k = 1,2, справедливо включение
®u0
®v0
,
то
uk - vk Î K .
u0 v0 .
Переходя в нем
10.
k ®к пределу при
u0 v0 .
в силу замкнутости конуса
K получим u0 - v0 Î K Þ
Упражнение. Какую упорядоченность вводит конус
{
}
K = u Î R1 u 0
в пространстве
R1 -
множестве действительных чисел,
а конус
{
}
K n = u = u1 ,L , u n Î R n u i 0, i = 1,L , n в пространстве
R n - множестве
Решение. Конус
{
n-
мерных векторов.
}
K = u Î R1 u 0
на множестве действительных чисел.
Конус
n-
{
}
K n = u = u1 ,L , u n Î R n u i 0, i = 1,L , n частично упорядочивает
мерные вектора по признаку: вектор
если каждая координата вектора
вектора
вводит естественную упорядоченность
v.
u
u
больше либо равен вектора
v,
больше либо равна соответствующей координаты
11.
2.10. Многокритериальная оптимизация. Пустьнабор из
n
функций, определенных на множестве
Задача состоит в том,
чтобы выбором элемента
Fi : ® R 1 , i = 1, , n
Î
произвольной природы.
минимизировать каждую из
этих функций. Такую задачу обычно называют задачей оптимизации с векторным
критерием. В общем случае эта задача, очевидно, решения не имеет. Однако можно
искать оптимум в смысле частичной упорядоченности значений векторного критерия,
задаваемой некоторым выпуклым конусом.
Fi ( u ) ® min, u Î U Ì R n , i = 1, L , r ,
r
значений
где U -компактное множество, а Fi Î C ( U ) . В пространстве R Рассмотрим задачу векторной оптимизации
критериев
введем частичную упорядоченность. Будем говорить, что точка
( 1) ö
æ
F
ç
1 ÷
÷
ç
÷
ç
÷
ç
L
÷
ç
÷
ç
÷
( 1)
ç
( 1) ÷
F =ç
Fi ÷
÷
ç
÷
ç
÷
ç
÷
L
ç
÷
ç
÷
ç
÷
( 1) ÷
ç
÷
ç
èFr ø
меньше точки
F(
2)
( 2) ö
æ
F
ç
1 ÷
÷
ç
÷
ç
÷
ç
L
÷
ç
÷
ç
÷
ç
( 2) ÷
=ç
,
Fi ÷
÷
ç
÷
ç
÷
ç
÷
L
ç
÷
ç
÷
ç
÷
( 2) ÷
ç
÷
ç
èFr ø
если
( 1)
( 2)
Fj £ Fj
12.
для всехj Î {1,L , r }
Упражнение 1.
и существует номер
i Î {1, L , r } ,
Построить выпуклый конус
KF ,
введенную частичную упорядоченность.
что
( 1)
( 2)
Fi < Fi .
который будет определять
ìï æF ö
ü
ïï
ïï ç 1 ÷
ïï
ç ÷
r
÷
Решение. K = ïí ç
L÷
Î R Fi ³ 0, " i Î {1,L , r } , $ j Î {1, L , r } : F j > 0ý.
ç
F
÷
ç
ïï ç ÷
ïï
÷
÷
ïîï ç
ïþ
èFr ø
ï
Докажем, что конус K F выпуклый. Пусть
( 1)
æ
ö
( 2)
æ
ö
F
ç
F
³
0
1 ³ 0÷
÷
ç
1
÷
ç
÷
÷
ç
ç
÷
÷
ç
ç
÷
L
÷
ç
L
÷
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
( 1)
ç
÷
2
(
)
÷
ç
Fi > 0÷
÷
ç
F
³
0
ç
÷
i
ç
÷
ç
÷
÷
ç
1
(
)
ç
÷
( 1)
( 2)
2
(
)
÷
ç
,
L
÷
l Î [ 0,1]
÷
F , F Î KF , F =ç
F
=
,
L
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
( 1)
÷
ç
( 2)
÷
ç
÷
ç
F
³
0
÷
ç
F
>
0
j
÷
ç
j
÷
ç
÷
ç
÷
÷
ç
ç
÷
÷
ç
L ÷
ç
÷
L
ç
÷
ç
÷
ç
÷
ç
÷
ç
÷
( 1)
÷
ç
2
(
)
÷
ç
ç
F
³
0
è
ø
÷
ç
r
Тогда
èF ³ 0÷
ø
r
13.
æl F ( 1) +( 1- l ) F ( 2) ³ 0 ö÷
ç
1
1
÷
ç
÷
ç
÷
ç
L
÷
ç
÷
ç
÷
>0
ç
÷
}
÷
ç
l
¹
0
÷
ç
( 1)
( 2)
ç
÷
l Fi +( 1- l ) Fi > 0÷
ç
÷
ç
÷
ç
( 1)
( 1)
÷
ç
÷
L
l F +( 1 - l ) F = ç
Î KF
÷
÷
ç
ç
>
0
÷
64444744448l ¹ 1 ÷
ç
÷
ç
÷
( 1)
( 2)
ç
÷
l
F
+
1
l
F
>
(
)
ç
÷
j
j
ç
÷
÷
ç
÷
ç
L
÷
ç
÷
ç
÷
ç
1
2
(
)
(
)
÷
ç
÷
èl Fr +( 1- l ) Fr ³ 0 ø
Определение 15.
Точка
оптимальной по Парето,
выполнялось бы
u* ,
KF
u Î U,
оптимальная в смысле конуса
т. е. не существует такой точки
Fi ( u ) £ Fi ( u* ) " i = 1,L k
и
называется
для которой
$j Î {1, L k } : Fj ( u ) < F j ( u* ) .
Множество оптимальных по Парето точек обычно содержит более одной точки.
Полагаем
r
F ( u, l 1 , L l r ) = å l i Fi ( u ) , u Î U , l i > 0, i = 1, L , r.
i =1
14.
Теорема 21. Пусть точкаu* Î U
такова, что
F ( u* ) = min F ( u , l 1 , L l r ) , l i > 0, i = 1, L , r.
( 1)
uÎ U
Тогда точка
u* -
Доказательство.
для которой
оптимальна по Парето.
От противного приходим к существованию точки
u** Î U
Fi (u** ) £ Fi (u* ), " i = 1, L , r ,
$j Î {1, L , r } : F j (u** ) < F j (u* ).
Тогда
F ( u** , l 1 , L l r ) =
<F j ( u* )
6
4
47448
>0
>0
>0 Fr ( u* ) £
= l 1 F1 ( u** ) +L +l j Fj ( u** ) +L +l r Fr ( u** ) <
£ F1 ( u* )
< l 1 F1 ( u* ) +L +l j Fj ( u* ) +L +l 1r Fr ( u* ) = F ( u* , l 1 , L l r ) Þ
F ( u** , l 1 , L l r ) < F ( u* , l 1 ,L l r ) .
Последнее неравенство противоречит (1). Теорема доказана.
15.
Упражнение 2.Найти все точки Парето в задачи векторной оптимизации
2
F1 ( u ) = ( u - 1) ® min,
2
F2 ( u ) = ( u - 3) ® min,
u Î U = [ 0,3]
Решение. Полагаем
2
2
F ( u , l 1 , l 2 ) = l 1 ( u - 1) +l 2 ( u - 3) ® min, u Î R1 , l 1 , l 2 > 0
F '( u ) = 2l 1 ( u - 1) + 2l 2 ( u - 3) = 0 Þ ( l 1 +l 2 ) u - l 1 - 3l 2 = 0 Þ
l 1 + 3l 2
u* =
.
l 1 +l 2
Покажем, что
u* < 3.
u* Î ( 0,3) .
Неравенство
u* > 0 очевидно.
Проверим неравенство
Имеем
>0
>0
l 1 + 3l 2
< 3 Þ l 1 + 3l 2 < 3 l 1 + 3l 2 Þ 1 < 3
l 1 +l 2
Таким образом, точка u* является внутренней точкой множества U .
F ''( u ) = 2l 1 + 2l 2 > 0.
Тогда
u* -
При этом
точка минимума функции F и она
оптимальна по Парето. Построим область вех таких точек.
16.
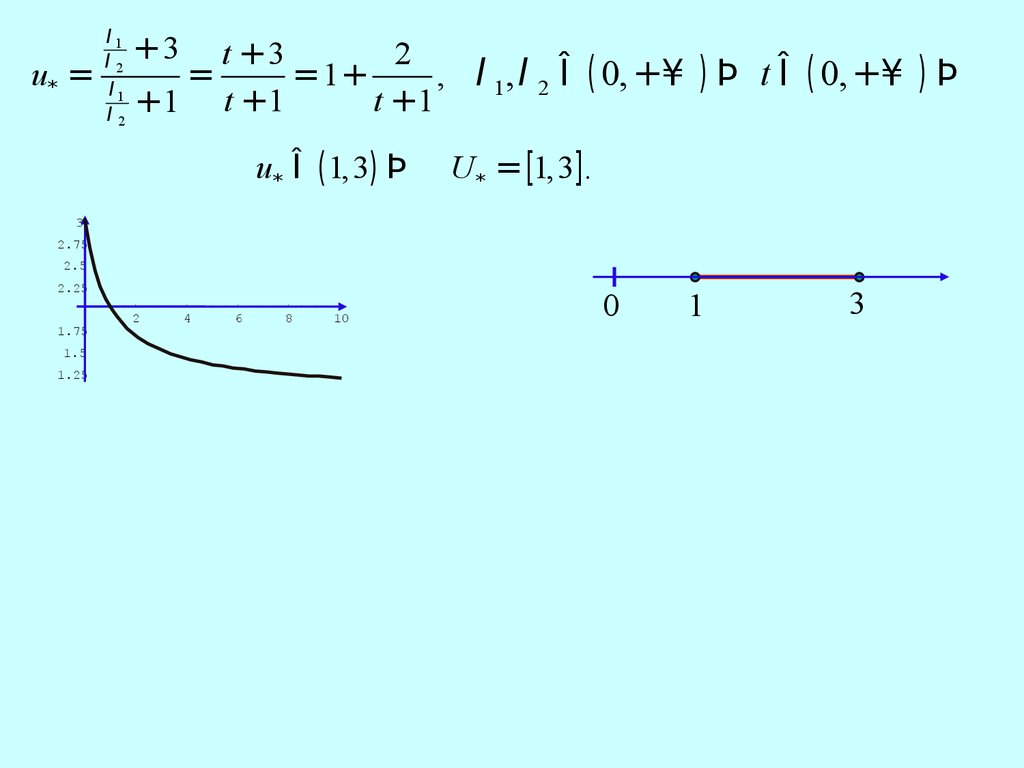
u* =l1
l2
l1
l2
+3
+1
=
t +3
2
=1+
, l 1 , l 2 Î ( 0, +¥ ) Þ t Î ( 0, +¥ ) Þ
t +1
t +1
u* Î ( 1,3) Þ
U * = [1,3].
3
2.75
2.5
2.25
1.75
1.5
1.25
2
4
6
8
10
0
1
3

















 Математика
Математика Программирование
Программирование








