Похожие презентации:
Выпуклый анализ. Выпуклые множества. Лекция 5
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 52. ВЫПУКЛЫЕ МНОЖЕСТВА
2.
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)2.2. Аффинные множества.
2.3. Размерность множества.
2.4. Операции над выпуклыми множествами.
3.
2.2. Аффинные множества.Определение 2. Множество
u1 , u2 Î M , l Î R1
M Rn
называется аффинным,
справедливо включение
если для всех
lu1 + (1 - l )u2 Î M .
Геометрический смысл данного определения состоит в том, что аффинное множество
вместе с любыми своими точками содержит и всю прямую, проходящую через эти точки.
Очевидно, что аффинные множества выпуклы. Пустые и одноточечные множества
принимаются аффинными по определению.
Теорема 2. Любой сдвиг аффинного множества является аффинным множеством.
Доказательство. Пусть
A Î R n - аффинное множество
M = A + { u0 } . Требуется доказать, что множество M
Действительно, для всех
ÎA
и
u0 Î R n .
является аффинным.
u1 , u 2 Î M и l Î R 1 имеем
ÎA
u1 = a1 + u0 , u2 = a2 + u0 ,
a1 , a2 Î A
ul = lu1 + ( 1 - l ) u2 = l ( a1 + u0 ) + ( 1 - l ) ( a2 + u0 ) =
Î Aафинное
6 44
7 4 48
= l a1 + ( 1 - l ) a2 + u0 Î A + { u0 } = M .
Теорема доказана.
Полагаем
4.
L R n называется подпространствомa , b Î R 1 и u , v Î L следует a u + b v Î L.
Определение 3. Множество
пространства
R n , если для всех
L R n будет подпространством тогда и только
u , v Î L следует u + v Î L и a u Î L.
Упражнение. Доказать, что множество
тогда, когда для всех
a Î R1
и
L R n - подпространство. Тогда
a u + b v Î L. Для a = 1, b = 1 Þ u Î+L v Î L и для b = 0 Þ a u Î L.
6 47 48
ÎL
ÎL
Достаточность. ( a u ) + ( b v ) Þ ( a u ) + ( b v ) Î L
n
Все пространство R и любое его подпространство являются аффинными множествами.
Теорема 3. Пусть A R n - аффинное множество, и 0 Î A. Тогда A Доказательство. Необходимость. Пусть
подпространство.
Доказательство. Для всех
u , v Î A, a Î R1имеем
определение афинного множества
au = au + ( 1-a ) × 0 Î A ,
( 1)
ÎAв силу ( 1)
6 4 44
7 4 4 48
ÎA
6447
448
1 ö
æ1
u + v = 2 × ç u + v ÷ = 2 × éê 1 u + æç1 - 1 ö÷ × v ùú Î A.
2 ø
è2
è 2ø û
ë2
Теорема доказана.
5.
A RnA = L + { u0 } ,
Теорема 4. Всякое аффинное множество
представимо в виде
( 2)
где L подпространство, однозначно определяемое множеством
произвольная точка множества A.
Доказательство. Пусть u0 Î A. Положим L = A - u0 .
множество
L - аффинное,
u0 Î A Þ 0 Î L.
причем
A,
{ }
а
u0 -
В силу теоремы 2
Тогда по теореме 3
L-
подпространство. Убедимся, что оно не зависит от выбора точки u0 . В самом деле, пусть
L1 = A - { u1} , u1 Î A.
A - { u0 } = L.
Из (2) следует
Пусть
u Î L.
ÎL
Тогда имеет место включение
Докажем, что
ÎL
u Î L1.
( 3)
ÎA
u1 - u0 Î L.
По свойству подпространств
u + ( u1 - u0 ) Î L Þ u Î L - { u1 - u0 } =
( 3) Þ= L1
6
4
7 48
64 7 48
= L + { u0 } - { u1} = A - { u1} Þ u Î A - { u1} = L1.
( 2 ) Þ= A
Таким образом, доказано, что
L1 L.
Тогда
L = L1
L L1.
Аналогично доказывается обратное вложение
и теорема доказана.
6.
Определение 4.Подпространство
L
из представления (1)
называется подпространством, параллельным множеству
A = L + { u0 }
( 1)
A.
Дадим геометрическую иллюстрацию полученных результатов.
При
n=2
подпространство представляет собой прямую, проходящую через начало координат,
а аффинное множество – произвольную прямую на плоскости. Теорема 3 утверждает,
что для любой прямой на плоскости существует единственная прямая, проходящая
через начало координат, ей параллельная.
u2
u 2 = ku1 + b
u 2 = ku1
0
u1
Теорема 5. Пересечение любого числа аффинных множеств является аффинным
множеством. Доказательство аналогично доказательству теоремы 1.
7.
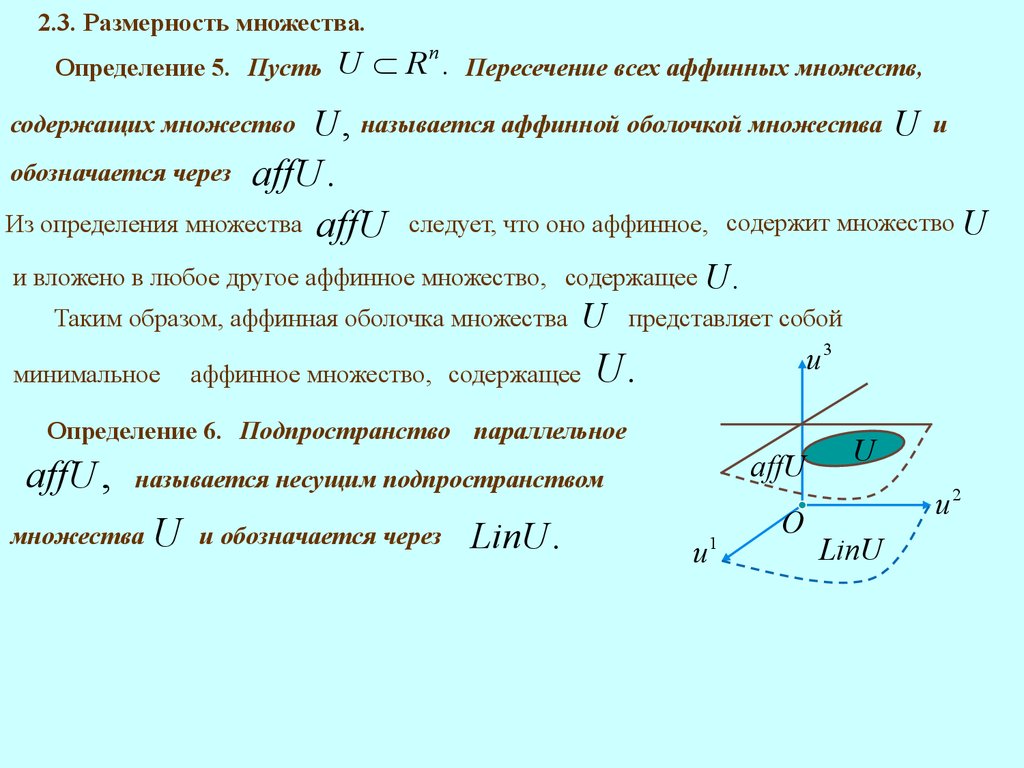
2.3. Размерность множества.Определение 5. Пусть
содержащих множество
U Rn .
Пересечение всех аффинных множеств,
U , называется аффинной оболочкой множества U
affU .
Из определения множества affU
и
обозначается через
следует, что оно аффинное, содержит множество U
и вложено в любое другое аффинное множество, содержащее
Таким образом, аффинная оболочка множества
минимальное
аффинное множество, содержащее
U
U.
представляет собой
u3
U.
Определение 6. Подпространство параллельное
affU ,
affU
называется несущим подпространством
множества
U
и обозначается через
LinU .
u
1
O
U
u2
LinU
8.
Определение 7. Размерностью множества UR n называется размерность
несущего пространства его аффинной оболочки.
Согласно принятому определению отрезок
[ u, v ] = { ua = a u + ( 1 - a ) v a Î [ 0,1]}
u , v Î R n , u ¹ v,
соединяющий две точки
имеет размерность 1, так как
его аффинной оболочкой является прямая
{
}
aff [ u , v ] = ua = a u + ( 1 - a ) a Î R1 .
u
aff [ u , v ]
u
u3
3
u
O
v
u
Lin [ u , v ]
O
2
u1
1
Размерность шара
O( u 0 , R ) R n
равна
n.
u2
9.
2.4. Операции над выпуклыми множествами.К числу операций над выпуклыми
множествами, сохраняющих их выпуклость относятся:
взятия линейной алгебраической комбинации
операции пересечения,
и линейного преобразования.
Теорема 6. Любая линейная комбинация конечного числа выпуклых множеств выпукла.
U1 ,L ,U m R n - выпуклые множества
m
U = å liU i . Для всех u , v Î U справедливо представление
Доказательство. Пусть
i =1
m
ÎU i
( u)
i i
m
ÎU i
( v)
i i
ai( u ) , ai( v ) Î U i , i = 1,L , m.
u = ål a , v = ål a ,
i =1
Тогда при всех
a Î [ 0,1]
i =1
имеем
m
= å lia a
i =1
m
a u + (1 - a )v = a å li ai + (1 - a )å li ai( v ) =
i =1
m
и
( u)
i
m
+ å li (1 - a )ai
i =1
( v)
( u)
i =1
i
6 4 Î4Uвыпуклост
4
7 4 4ь 48
ÎU i
m
é ÎU( ui )
( v) ù
= å li êa ai + ( 1 - a ) ai ú.
i =1
êë
úû
10.
i6 4 Î4Uвыпу
4
7 клость
4 4 48
ÎU i
m
é ÎU( ui )
( v ) ù Из выпуклости множества
a u + (1 - a )v = å li êa ai + ( 1 - a ) ai ú.
i =1
êë
úû
a ai( u ) + ( 1 - a ) ai( v ) Î U i , i = 1,L , m,
Ui
следует
Тогда
ÎU i
6
4
4
4
7 4 4 48
m
( u)
( v) ù
é
a u + (1 - a )v = å li ëa ai + ( 1 - a ) ai û. Î
i =1
Теорема доказана.
Теорема 7.
Пусть
U Rn
выпуклое множество и
( a + b ) × U = aU + b U .
Доказательство. Вложение
(a + b ) × U aU + bU
m
ålU
i =1
i
i
= U.
a ³ 0, b ³ 0.
Тогда
( 1)
было доказано в
предыдущей лекции в общем случае без предположения о выпуклости множества
и положительности чисел
a
и
b.
U
В условиях теоремы докажем обратное вложение
( a + b ) × U É aU + b U .
11.
Будем предполагать, чтоa + b > 0.
64 70 48
0
0
( a + b ) ×U = a U + b U .
( 1)
В противном случае
очевидна. Пусть
a =b =0
u Îa U + b U .
и формула (1)
Тогда
}³0
}³0
æ
ö
ÎU
ÎU
b
ç a
÷
u1 +
u2 ÷ ,
u = a u1 + b u2 , u1 , u2 Î U Þ u = ( a + b ) ç
a +b ÷
ça + b
è
ø
выпуклость
æ a
ö U
b
a
b
a
b
u1 +
u2 ÷ Î U .
³ 0,
³ 0,
+
=1Þ ç
a +b
a +b
a +b ø
a +b a +b
èa + b
Таким образом,
u Î ( a + b ) U Þ ( a + b ) × U É aU + b U Þ ( a + b ) × U = a U + b U .
и теорема доказана.
Пусть U
Rn
и
A-
квадратная матрица
Определение 8. Образом множества
называется множество
U
n-
го порядка.
при линейном преобразовании
A ( U ) = { v = Au u Î U } .
A
12.
Теорема 8. При линейном преобразовании образ непустого компактного выпуклогомножества является непустым компактным выпуклым множеством.
Доказательство.
преобразования.
Для всех
Ограничимся доказательством выпуклости образа линейного
Пусть
v1 , v2 Î A ( U ) Þ vi = Aui , ui Î U , i = 1, 2.
a Î [ 0,1]
выполнено
ÎUвыпуклость
æ6 4
4 7 4 48 ö
a v1 + ( 1 - a ) v2 = a Au1 + ( 1 - a ) Au2 = A ç a u1 + ( 1 - a ) u2 ÷ .
ç
÷
è
ø
В силу выпуклости множества U имеет место включение a u1 + ( 1 - a ) u2 Î U .
Тогда
ÎU
4 48 ö
æ 6 4 47
a v1 + ( 1 - a ) v2 = A ç a u1 + ( 1 - a ) u2 ÷ Î A ( U )
ç
÷
è
ø
и выпуклость множества
A(U )
доказана.
Пример 5. Пусть
æ a 0ö
n = 2, A = ç
÷,
è0 bø
U = O ( 0, 1) =
ìïæ u1 ö 1 2
üï
2 2
íç 2 ÷ ( u ) + ( u ) £ 1ý .
ïîè u ø
ïþ
13.
ìïæ v1 ö æ a 0 ö æ u1 ö 1 22 2
A ( O ( 0,1) ) = íç ÷ = ç
÷ç 2 ÷ ( u ) + ( u )
2
ïîè v ø è 0 b ø è u ø
ìïæ v1 ö æ au1 ö 1 2
üï
2 2
= íç 2 ÷ = ç 2 ÷ u + u £ 1ý ,
ïîè v ø è bu ø
ïþ
æ1
-1
1
1
1
1
æ v ö æ a 0öæ u ö
æ u ö æ a 0ö æ v ö
ça
=
Þ
=ç
= ç
ç 2÷ ç
÷ç 2 ÷
ç
÷
ç
÷
÷
2
2
èv ø è 0 bøèu ø
èu ø è 0 bø èv ø
ç0
ç
è
1
2
v
v
u1 = , u 2 = Þ
u 2 ( v2 )
üï
£ 1ý =
ïþ
( ) ( )
a
b
A ( O ( 0,1) ) =
b
1
2
ìïæ v1 ö
üï
æ
ö
æ
ö
v
v
2
= íç 2 ÷ Î R ç ÷ + ç ÷ £ 1ý .
èaø èbø
ïîè v ø
ïþ
2
2
- a -1
ö
0÷ 1
æv ö
÷ç 2 ÷ Þ
1 ÷èv ø
÷
bø
1
O
1
-b
-1
a
u1 ( v1 )
14.
Упражнение 1.Пусть
Построить множество
Решение.
(1)
u2
ì
-7u1 - 2u2 £ -14, ü
ïæ u1 ö
ï
U = íç ÷ 5u1 + 6u2 £ 30, ý
ïè u2 ø -3u - 8u £ -24, ï
1
2
î
þ
æ 2 0ö
A ( U ) , где A = ç
÷ . Убедиться в его выпуклости
è 0 3ø
-7u1 - 2u2 £ -14, ( 1)
Построение множества U .
5u + 6u £ 30,
( 2)
1
-3u1 - 8u2 £ -24,
8
6
(3)
4
2
-6 -4 -2 0
-2
-4
-6
2
( 1)
2 4 6 8 10
(2)
u1
( 2)
( 3)
u1 = 0 Þ u2 = 7,
u1 = 2 Ü u2 = 0.
u1 = 0 Þ u2 = 5,
u1 = 6 Ü u2 = 0.
( 3)
u1 = 0 Þ u2 = 3,
u1 = 8 Ü u2 = 0.
15.
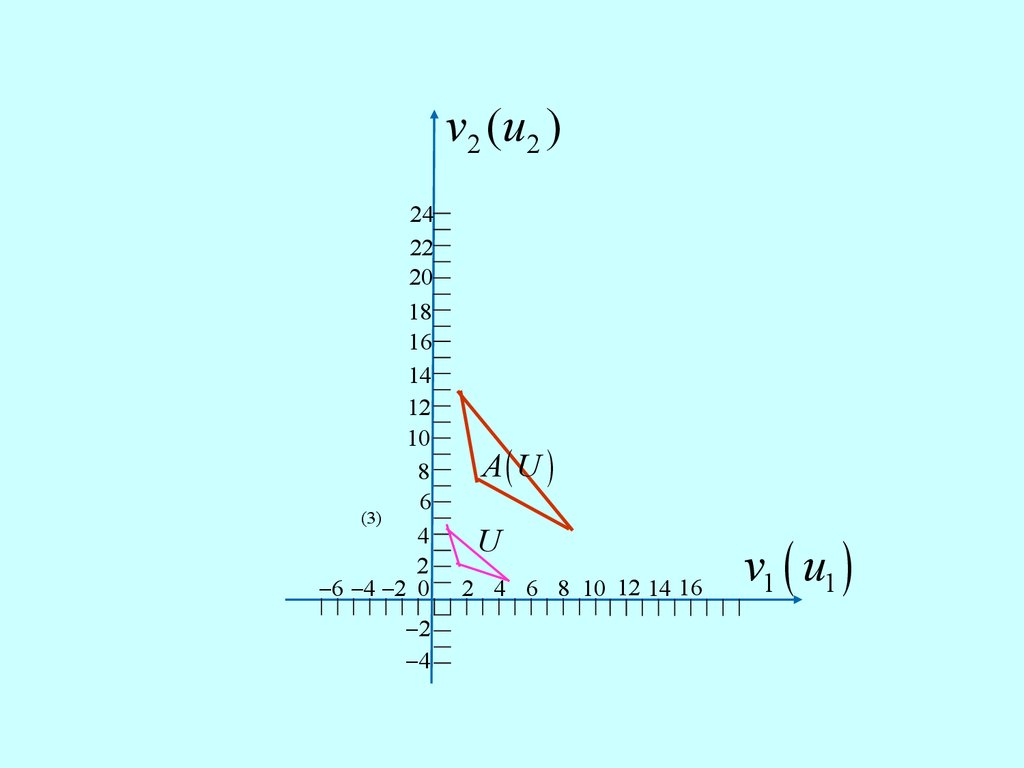
Построение множестваA( U ) .
ì 1
ïæ v ö
A ( U ) = íç 2 ÷ =
ïè v ø
î
-7u1 - 2u2 £ -14, ü
æu ö
ï
A ç 2 ÷ 5u1 + 6u2 £ 30, ý .
è u ø -3u - 8u £ -24, ï
1
2
þ
1
-1
1
1
0
v
v
v
2
0
æ
ö
æ
æ u1 ö
æ
ö
æ
ö
æ
ö
æ
ö
1
1
1
2
2 v1 ö
-1
ç ÷= A ç ÷=ç
ç ÷ = ç0 1 ÷ç ÷ = ç 1 v ÷
÷
è u2 ø
è v2 ø è 0 3 ø è v2 ø è
3 ø è v2 ø
è3 2ø
A( U ) =
ì
-7 ( 12 v1 ) - 2 ( 13 v2 ) £ -14, ü
ïïæ v1 ö
ïï
1
1
= íç 2 ÷ 5 ( 2 v1 ) + 6 ( 3 v2 ) £ 30, ý Þ
ïè v ø
ï
1
1
-3 ( 2 v1 ) - 8 ( 3 v2 ) £ -24, ïþ
ïî
7
2
- v1 - v2 £ -14, ( 1)
2
3
5
v1 + 2v2 £ 30,
( 2)
2
3
8
- v1 - v2 £ -24 ( 3)
2
3
Þ
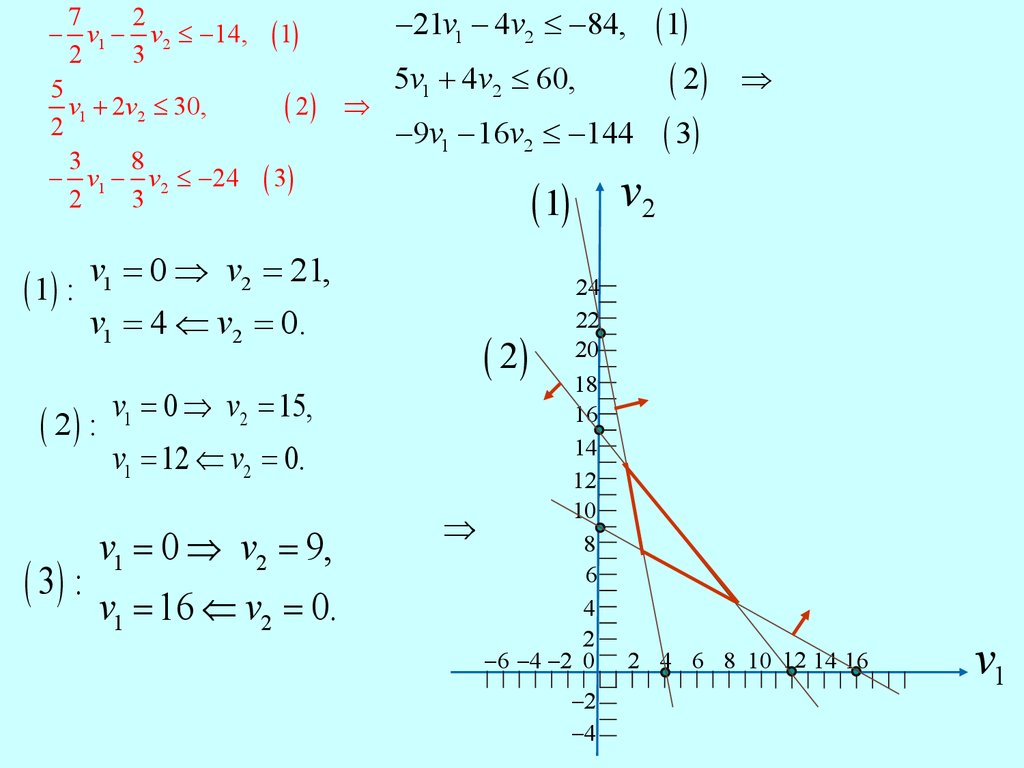
16.
72
- v1 - v2 £ -14, ( 1)
2
3
5
v1 + 2v2 £ 30,
( 2)
2
3
8
- v1 - v2 £ -24 ( 3)
2
3
( 1) :
-21v1 - 4v2 £ -84,
Þ
5v1 + 4v2 £ 60,
-9v1 - 16v2 £ -144
v1 = 4 Ü v2 = 0.
( 2) :
v1 = 12 Ü v2 = 0.
( 3) : v
1
= 16 Ü v2 = 0.
24
22
20
2
18
16
14
12
10
8
6
4
2
-6 -4 -2 0
( )
v1 = 0 Þ v2 = 15,
v1 = 0 Þ v2 = 9,
Þ
v2
( 1)
v1 = 0 Þ v2 = 21,
( 1)
( 2)
( 3)
Þ
-2
-4
2 4 6 8 10 12 14 16
v1
17.
v2 (u2 )24
22
20
18
16
14
12
10
8
6
(3)
4
2
-6 -4 -2 0
-2
-4
A( U )
U
2 4 6 8 10 12 14 16
v1 ( u1 )











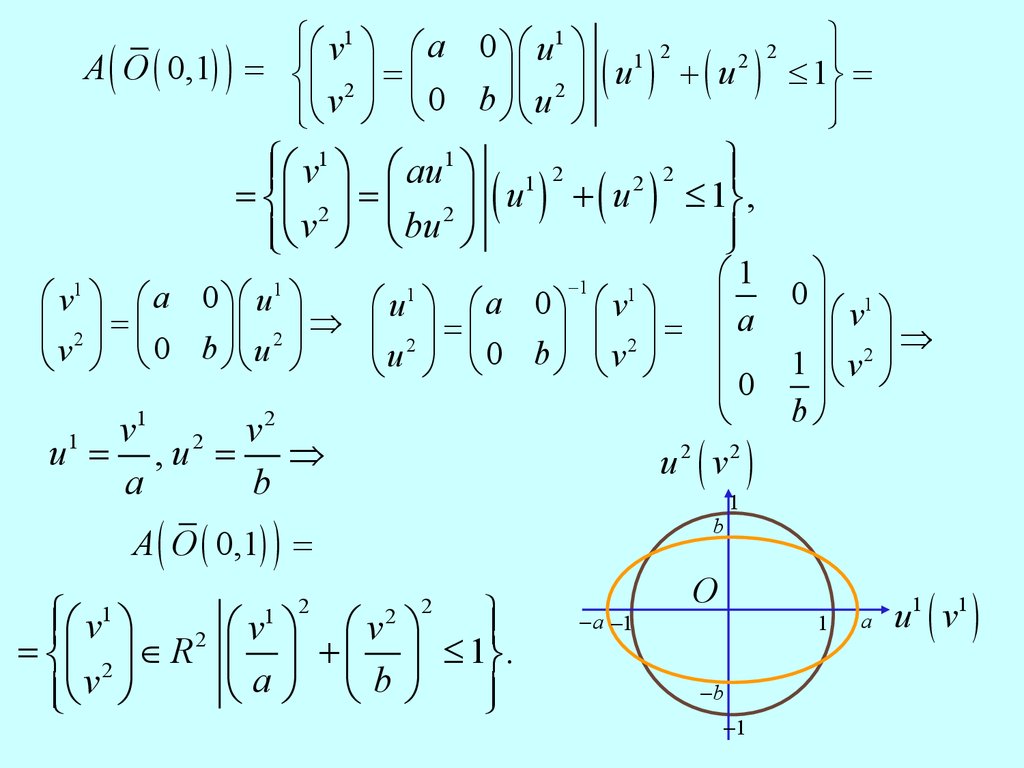



 Математика
Математика Программирование
Программирование








