Похожие презентации:
Выражения с логарифмами
1. ПОВТОРЕНИЕ
Урок № 4ПОВТОРЕНИЕ
Выражения с логарифмами
log a b
log – знак логарифма,
a – основание логарифма,
b – выражение под логарифмом
И не пытайся понять мою душу:
там такие, сударь ты мой, логарифмы!
Авессалом Подводный. Отдельные мысли
2.
ОПРЕДЕЛЕНИЕlog a b x ,
b 0
ax b
a 0
Теория
a 1
ОСНОВНОЕ
ЛОГАРИФМИЧЕСКОЕ
ТОЖДЕСТВО
a
loga b
b
ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
log 10 b lg b
log e b ln b
СВОЙСТВА ЛОГАРИФМОВ
1) log a 1 0 2) log a a 1
3) log a b log a c log a (bc)
b
4) log a b log a c log a
5) log a b r r log a b
c
log c b
1
1
6) log a k b log a b
7) log a b
8) log a b
k
log c a
log b a
a
logc b
b
logc a
3.
=хУстно
4 16
х
Логарифмом положительного числа b по основанию a, где
a 0 a 1
называется показатель степени в которую нужно возвести
a, чтобы получить b.
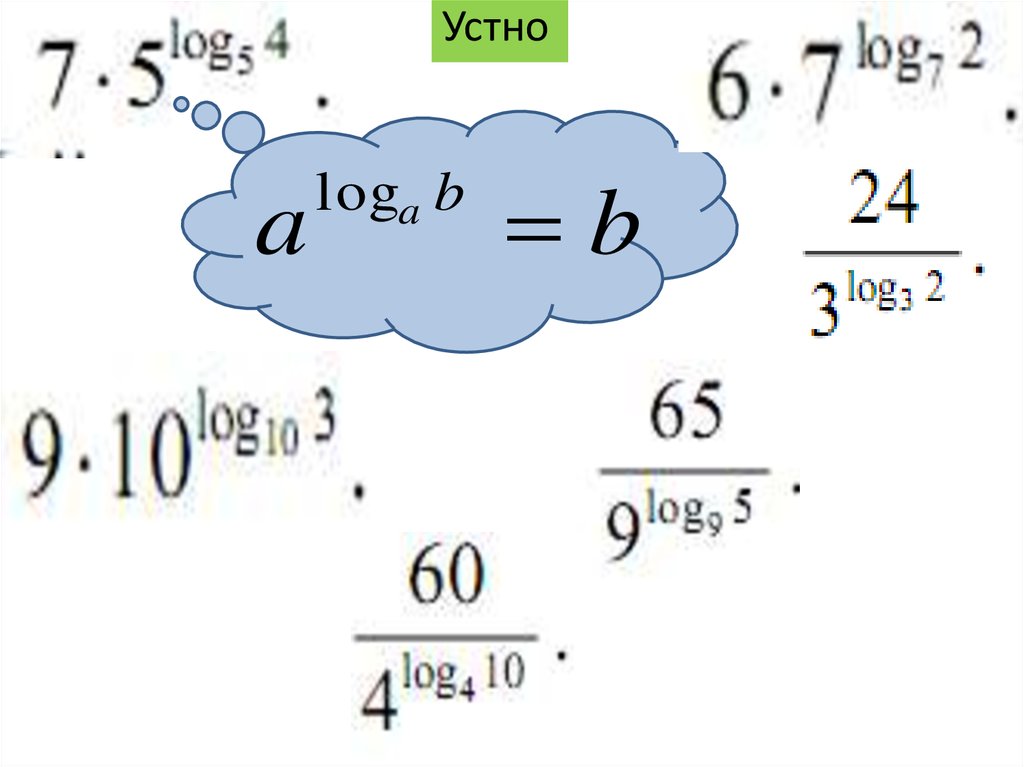
4.
Устноa
loga b
b
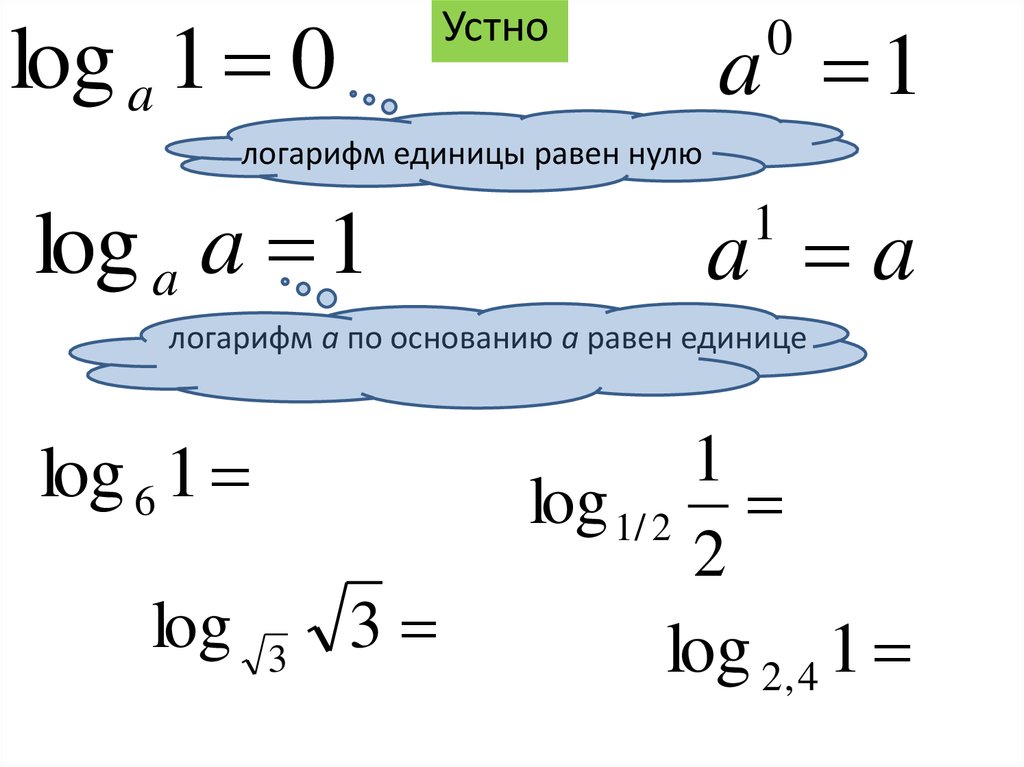
5.
log a 1 0a 1
Устно
0
логарифм единицы равен нулю
log a a 1
a a
1
логарифм a по основанию a равен единице
log 6 1
log
log 1/ 2
3
3
1
2
log 2, 4 1
6.
Устноlog a (bc) log a b log a c
логарифм произведения
положительных множителей
равен сумме логарифмов
этих множителей
b
log a
c
log a b log a c
логарифм частного
положительных числителя и знаменателя
равен разности
логарифма числителя и логарифма знаменателя
7.
УстноВычислите
8.
Предложите,как лучше запомнить данные две формулы?
Устно
log a b r log a b
r
логарифм степени равен
произведению
показателя степени
на логарифм основания
log a k
1
b log a b
k
9.
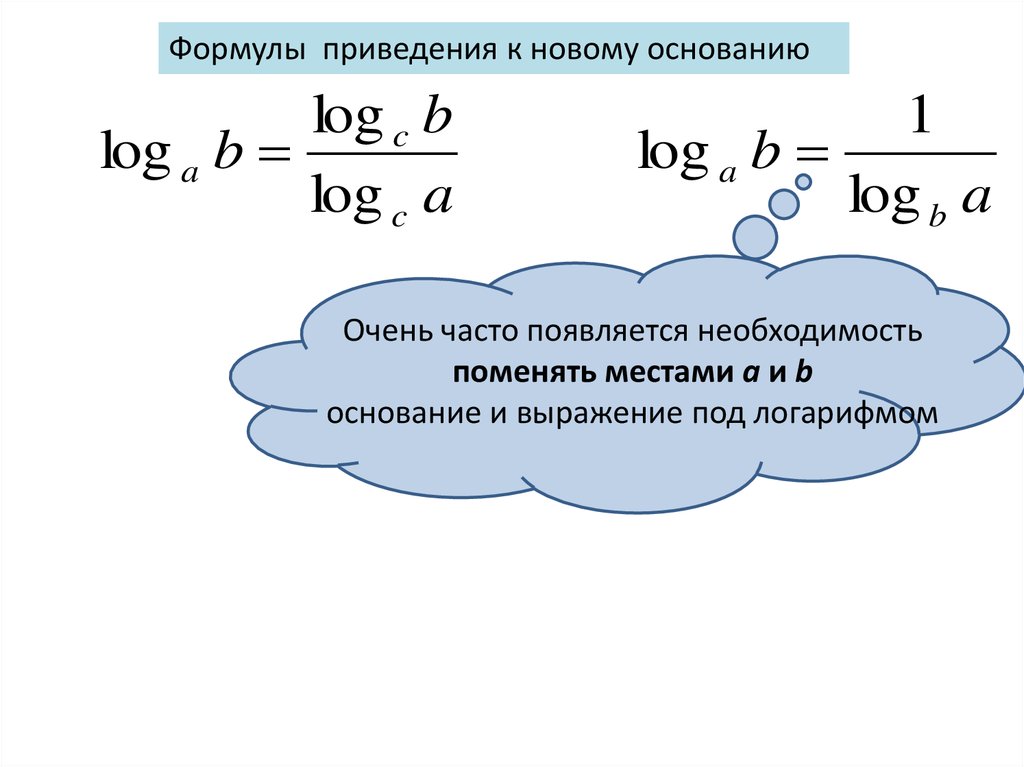
Устно10.
Формулы приведения к новому основаниюlog c b
log a b
log c a
1
log a b
log b a
Очень часто появляется необходимость
поменять местами a и b
основание и выражение под логарифмом
11.
Устно12.
ПисьменноВ классе нечётные номера, дома – чётные.
1
6
2
7
3
4
5
8
9
13.
Письменно10
16
11
17
12
13
14
15
18
19
14.
Письменно20
21
Дополнительная задачка
Домашнее задание № 4
В классе нечётные номера, дома – чётные.
15.
х 2 3х ax 2a 2 3a0
( х 3)( х 3)
Дробь равна нулю,
если числитель равен нулю,
а знаменатель нулю не равен.
х 2 х(3 a) (2a 2 3a)
0
( х 3)( х 3)
х 2 х(3 a) (2a 2 3a) 0
( х 3)( х 3) 0
Уравнение будет иметь ровно один корень, если
1) дискриминант квадратного уравнения равен нулю и корни не
совпадают с числами 3 и -3;
2) дискриминант положителен и один из корней равен 3 или -3.
{
1) D=(3-a)²+4(2a²-3a)=0
-9+3(3-a)+2a²-3a≠0
-9-3(3-a)+2a²-3a≠0
{
2) D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
16.
1{
D=(3-a)²+4(2a²-3a)=0
-9+3(3-a)+2a²-3a≠0
-9-3(3-a)+2a²-3a≠0
2
{
D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
1 D=(3-a)²+4(2a²-3a)=0 -9+3(3-a)+2a²-3a≠0 -9-3(3-a)+2a²-3a≠0
9-6a+a²+8a²-12a=0
2a²-6a≠0
2a²≠18
9a²-18a+9=0 |:9
a≠0 a≠3
a≠-3 a≠3
a²-2a+1=0
(a-1)²=0
При a=1 уравнение имеет ровно одно решение.
a=1
2 D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
(a-1)²>0
a=0 a=3
a=-3 a=3
a≠1
При a=0 и a=-3 уравнение имеет ровно одно решение.
Ответ: при a=0, a=1, a=3 исходное уравнение
имеет ровно одно решение.






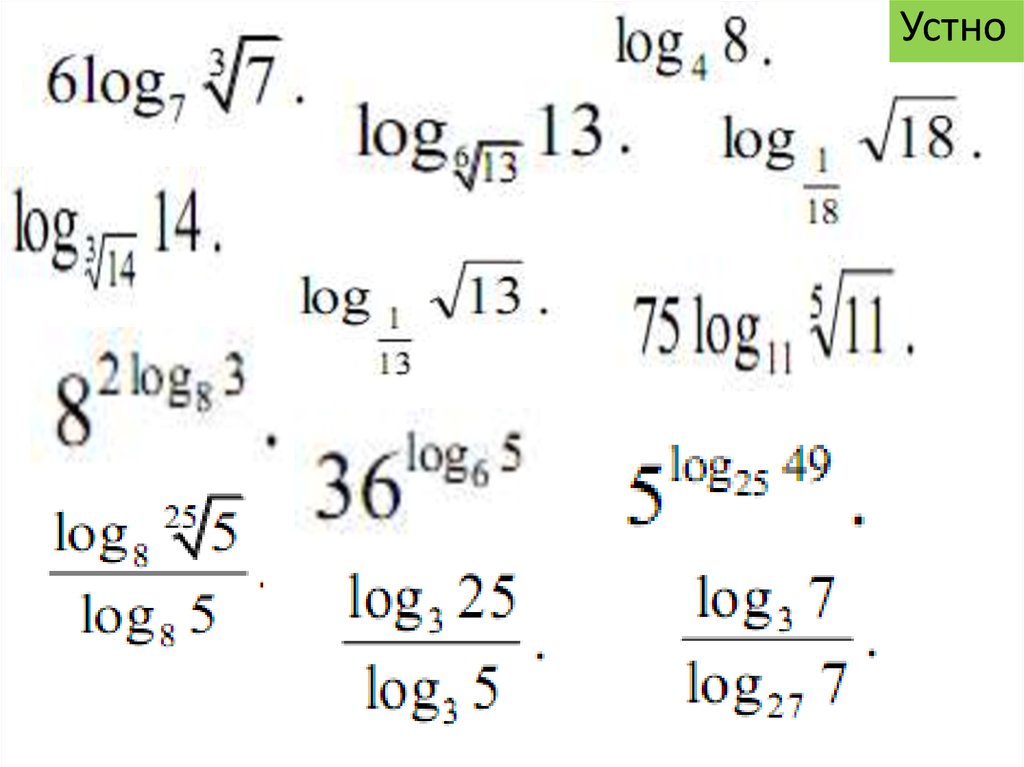
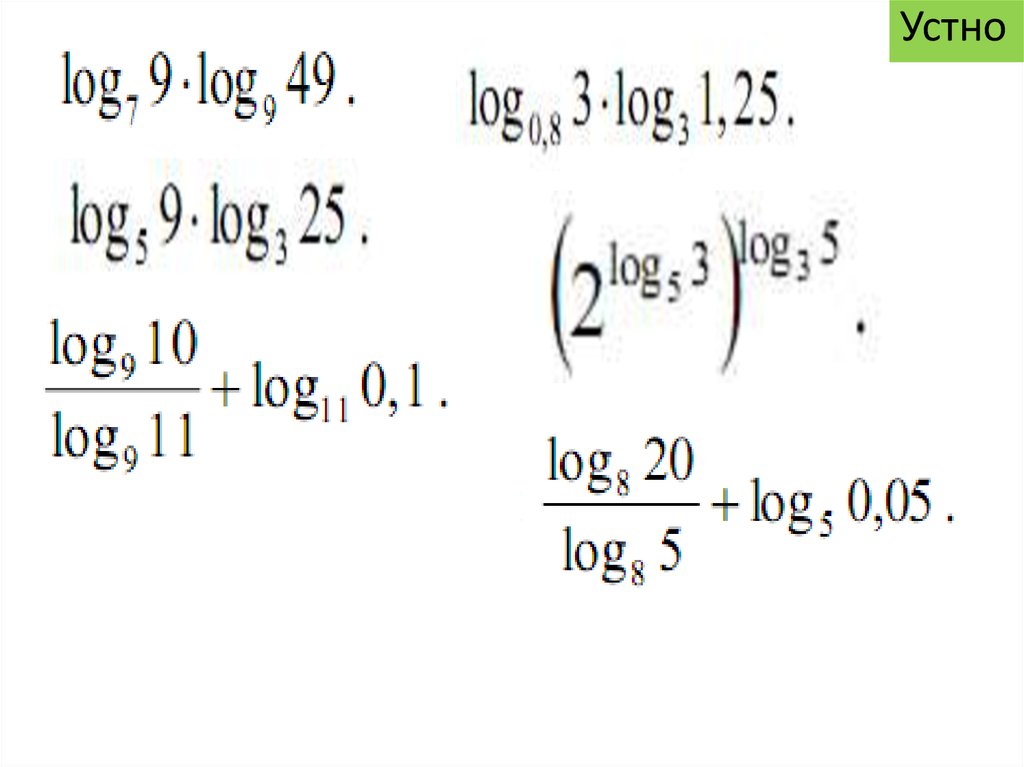





 Математика
Математика








