Похожие презентации:
Комплексные частотные характеристики линейных электрических цепей
1. Комплексные частотные характеристики линейных электрических цепей
Задачаанализа
электрической цепи была
сформулирована ранее
как задача определения
реакции
цепи
на
заданное
внешнее
воздействие.
Пусть для некоторой линейной электрической цепи это
воздействие задано в виде токов и напряжений нескольких
независимых источников тока и напряжения, а искомая
реакция (отклик) цепи представляет собой совокупность
токов или напряжений отдельных элементов (нагрузок).
2. Комплексные частотные характеристики линейных электрических цепей
Вынесем из рассматриваемой цепи ветви, содержащиенезависимые источники тока и напряжения, а также ветви,
токи или напряжения которых подлежат определению.
Оставшуюся часть цепи, содержащую идеализированные
пассивные элементы и, возможно, управляемые источники,
представим в виде многополюсника.
Входными будем называть пару зажимов (полюсов), к
которым подключается каждый из независимых источников,
задающих внешнее воздействие на цепь.
Зажимы, служащие для подключения нагрузки, т. е. ветви, ток
или напряжение которой необходимо определить, назовем
выходными.
3. Комплексные частотные характеристики линейных электрических цепей
Стороной многополюсника или портом называется паразажимов, которые служат входом, выходом или и входом, и
выходом одновременно.
Из определений входных и выходных зажимов следуют
важные
особенности
зажимов,
образующих
порт
многополюсника:
− ток, втекающий через один зажим порта, равен току,
вытекающему через другой зажим этого же порта;
− между парами полюсов, принадлежащих к разным портам,
не должно быть никаких внешних по отношению к
многополюснику соединений (внутри многополюсника
соединения естественно могут быть).
4. Комплексные частотные характеристики линейных электрических цепей
Зажимы, образующие одну сторону многополюсника,обозначим одинаковыми цифрами (со штрихом и без штриха)
1-1’, 2-2’ . . ., n-n’. В зависимости от числа сторон различают
односторонние,
двусторонние
и
n-сторонние
многополюсники.
Пусть внешнее воздействие на цепь задано только на одной
паре полюсов v-v’: x(t)=xv(t) и необходимо найти реакцию
цепи также только на одной паре полюсов k-k’: s(t)=sk(t).
Исследуемую цепь удобно рассматривать как двусторонний
четырехполюсник.
Если
v=k,
то
цепь
становится
односторонней, т. е. превращается в двухполюсник.
5. Комплексные частотные характеристики линейных электрических цепей
Ограничимсярассмотрением
случая
гармонического
внешнего воздействия; при этом от соотношений между
мгновенными значениями реакции цепи sk(t) и внешнего
воздействия xv(t) можно перейти к соотношениям между их
комплексными изображениями.
По
определению,
комплексной
частотной
характеристикой (частотным коэффициентом передачи)
цепи называется отношение комплексных изображений
отклика и воздействия:
H k j Smk / X m Sk / X
6. Комплексные частотные характеристики линейных электрических цепей
Размерность комплексной частотной характеристики (КЧХ)равна отношению размерностей отклика цепи и внешнего
воздействия. В зависимости от того, какие величины (токи или
напряжения) рассматриваются в качестве откликов и внешних
воздействий, КЧХ может иметь размерность:
- сопротивления (внешнее воздействие − iv, реакция цепи − uk),
- проводимости (внешнее воздействие − uv, реакция цепи − ik)
или быть безразмерной (внешнее воздействие − iv, реакция
цепи − ik, либо внешнее воздействие − uv, реакция цепи − uk).
7. Комплексные частотные характеристики линейных электрических цепей
Как и всякое комплексное число, КЧХ цепи может бытьзаписана в показательной:
H k j H k e j k ( )
или алгебраической
Hk j H k jH k
форме.
Представляя комплексные изображения отклика и воздействия
в показательной форме
X m 2X X m e j x 2X e j x ;
Smk 2Sk Smk e j s 2Sk e j s
определяем модуль и аргумент КЧХ:
H k Smk / X m Sk / X ;
k s x .
8. Комплексные частотные характеристики линейных электрических цепей
Таким образом, модуль КЧХ равен отношению амплитудили действующих значений отклика цепи и внешнего
воздействия, а ее аргумент представляет собой разность
начальных фаз отклика и внешнего воздействия.
КЧХ цепи численно равна комплексной амплитуде реакции
цепи на воздействие, описываемое единичной гармонической
функцией, т. е. на воздействие гармонического тока или
выражения с единичной амплитудой и нулевой начальной
фазой.
9. Комплексные частотные характеристики линейных электрических цепей
Зависимости модуля Hkv(ω) и аргумента kv(ω) комплекснойчастотой характеристики от частоты ω называются
амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ)
характеристиками цепи.
АЧХ и ФЧХ цепи характеризуют зависимости от частоты
соответственно амплитуды и начальной фазы отклика цепи на
внешнее воздействие с Xmv=1 и x=0 .
10. Комплексные частотные характеристики линейных электрических цепей
Комплексные частотные характеристики цепи делятся навходные и передаточные.
Когда отклик и внешнее воздействие рассматриваются на
одних и тех же зажимах цепи, КЧХ называется входной.
Если отклик и внешнее воздействие задаются на разных
зажимах цепи, КЧХ называется передаточной.
11. Комплексные частотные характеристики линейных электрических цепей
Различают два вида входных и четыре вида передаточныххарактеристик.
H j Z j U / I
K k j U k / U
Y j I / U
G k j I k / I
Zk j U k / I
Yk j I k / U
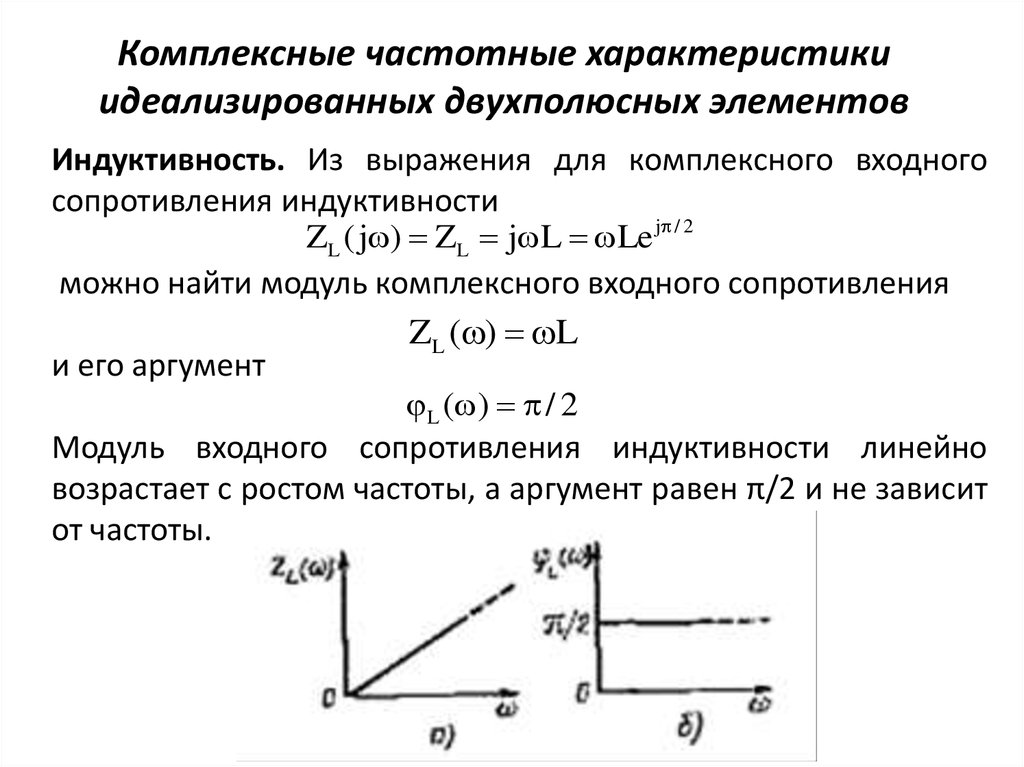
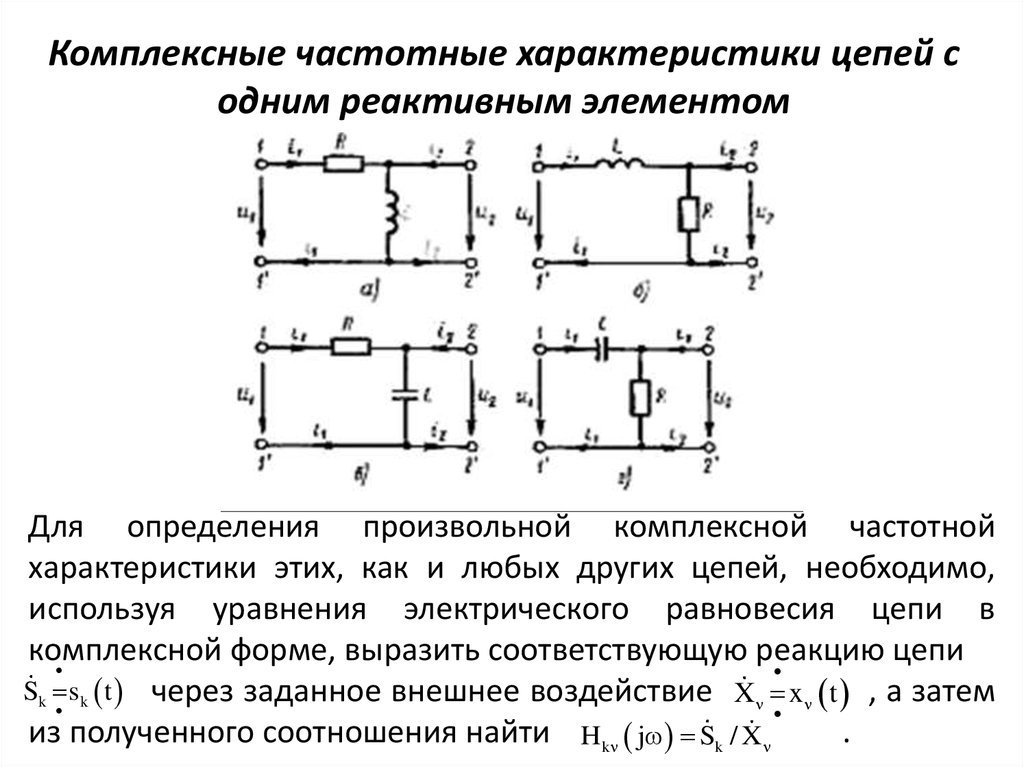
12. Графическое представление КЧХ
При графическом представлении комплексных частотныххарактеристик цепи обычно строят отдельно АЧХ и ФЧХ либо
изображают зависимости от частоты вещественной

















 Физика
Физика








