Задачи приводящие к задаче линейного программирования. (Тема 2)

1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ЗЛП

2. ЗАДАЧИ, ПРИВОДЯЩИЕ К ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП)

Задача о смесях
Задача о наилучшем распределении ресурсов
Задача о выборе оптимальной технологии
Задача о назначениях
Задача сменно-суточного планирования автобусного парка
Транспортная задача

3. Задача о смесях

Исходные данные:
m
n
–
число необходимых питательных в
– число
продуктов
– количество единиц i-го
a питания
питательного вещества, содержаij щееся в единице j-го вида продукта
– норма потребления i-го
b питания
i питательного вещества
c – цена j-го продукта питания
j
x – количество единиц j-го продукта,
j
используемого
в
рационе,
подлежащее определению
n
z c x min
j j
j 1
n
aij x j bi (i 1, m)
j 1
x 0 ( j 1, n)
j

4. Задача о наилучшем распределении ресурсов

Исходные данные:
чество видов выпускаемой продукции
ство– необходимых
для производства
рес
технологические
коэффициенты,
a
т.е.
количество
единиц
i-го
ij
ресурса,
необходимого
для
производства
единицы
j-го
вида
– полные объемы имеющихся
продукции
bi ресурсов
прибыль,
получаемая
при
cj–
реализации
единицы
j-го
вида
продукта.
x ( x ,..., x ,..., x ) – план выпуска продукции
n
1
j
n
z c j x j max
j 1
n
a x
j 1
ij
j
bi (i 1, m)
x j 0 ( j 1, n)

5. Задача о выборе оптимальной технологии

Исходные данные:
n
– количество технологий
m
– количество ресурсов
bi (i 1, m) – объём ресурсов i-го вида
– эффективность технологий,
c j ( j количество
1, n)
т.е.
конечной продукции
(в денежном эквиваленте),
производимой в единицу времени по
– расход i-го ресурса в единицу
j-й
a ij технологии
времени по j-й технологии
x j – время, в течение которого
продукция производится
по j-й
n
технологии
z c x max
j 1
n
a x
j 1
ij
j
j
j
bi (i 1, m)
x j 0 ( j 1, n)

6. Задача о назначениях

Исходные данные:
n – число видов работ
специалистов, выполняющих все виды работ
n –– число
эффективность выполнения i-ым
cспециалистом
ij
j-ой работы
1, i ый человек выполняет j ую работу
xi , j
0, i ый человек не выполняет j ую работу
c
x max
i, j i, j
n
x
j 1
i, j
n
x
i 1
i, j
1 (i 1, n)
1 ( j 1, n)

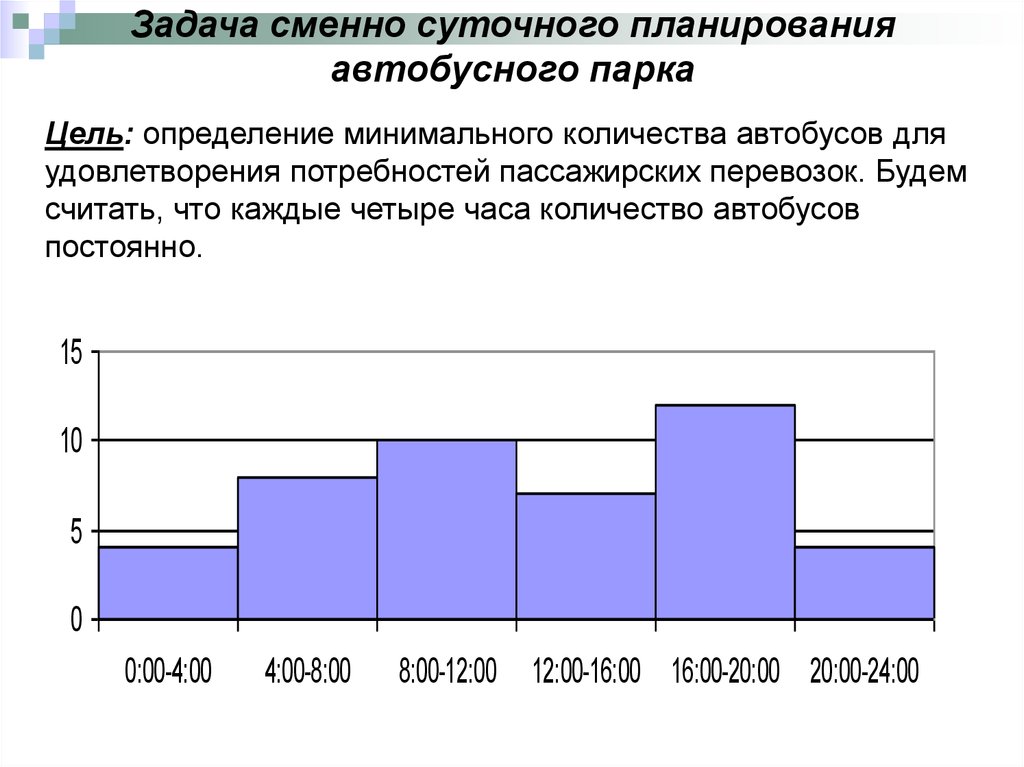
7. Задача сменно суточного планирования автобусного парка

Цель: определение минимального количества автобусов для
удовлетворения потребностей пассажирских перевозок. Будем
считать, что каждые четыре часа количество автобусов
постоянно.
15
10
5
0
0:00-4:00
4:00-8:00
8:00-12:00
12:00-16:00 16:00-20:00 20:00-24:00

8.

Постановка задачи
Считается, что автобус может находиться на линии только
восемь часов, и рабочий день водителя равен восьми часам.
Требуется определить количество автобусов в каждой из
рабочих смен так, чтобы оно было не меньше минимальной
потребности в них, при этом общее количество автобусов,
выходящих на линию в течение суток должно быть
минимальным.

9.

8 : 01 16 : 00
x1 10
16 : 01 24 : 00 x2 12
0 : 01 8 : 00 x3 8
x1 x2 x3 30
6
x
j 1
j
min
Решение:
xj 0
x1 x6 4 x1 0
x1 x2 8 x2 0
x2 x3 10 x3 0
x3 x4 7 x4 0
x4 x5 12 x5 0
x5 x6 4 x6 0
x1 x3 x5 0; x2 10; x4 12; x6 4.

10. Транспортная задача

Исходные данные:
m – число пунктов отправления ( Ai – пункт отправлени
n – число пунктов назначения( B j – пункт назначения)
ai (i 1, m) – объем продукта в пункте отправления
b j ( j 1, n) – потребность в пункте назначения
c ij
– затраты на перевозку единицы продукта из i-го пункта
отправления в j-ый пункт назначения
m
a
i 1
i
n
b j
j 1
m
n
ai b j (*)
i 1
j 1
Если выполняется условие (*), то перед нами транспортная задача
закрытого типа. В противном случае это – задача открытого типа.

11.

Cоставить такой план перевозок,
чтобы общая стоимость перевозок
была минимальной.
B1
B2
…
Bn
A1
X11, C11
X12, C12
…
X1n, C1n
A2
X21, C21
X22, C22
…
X2n, C2n
…
…
…
…
…
Am
Xm1, Cm1
Xm2 Cm2
…
Xmn, Cmn
m
n
c
i 1 j 1
x min
ij ij
n
xij ai , (i 1, m)
jm 1
x b , ( j 1, n)
ij
j
i 1
xij 0