Похожие презентации:
Статистическое изучение динамики социально - экономических явлений
1.
2.
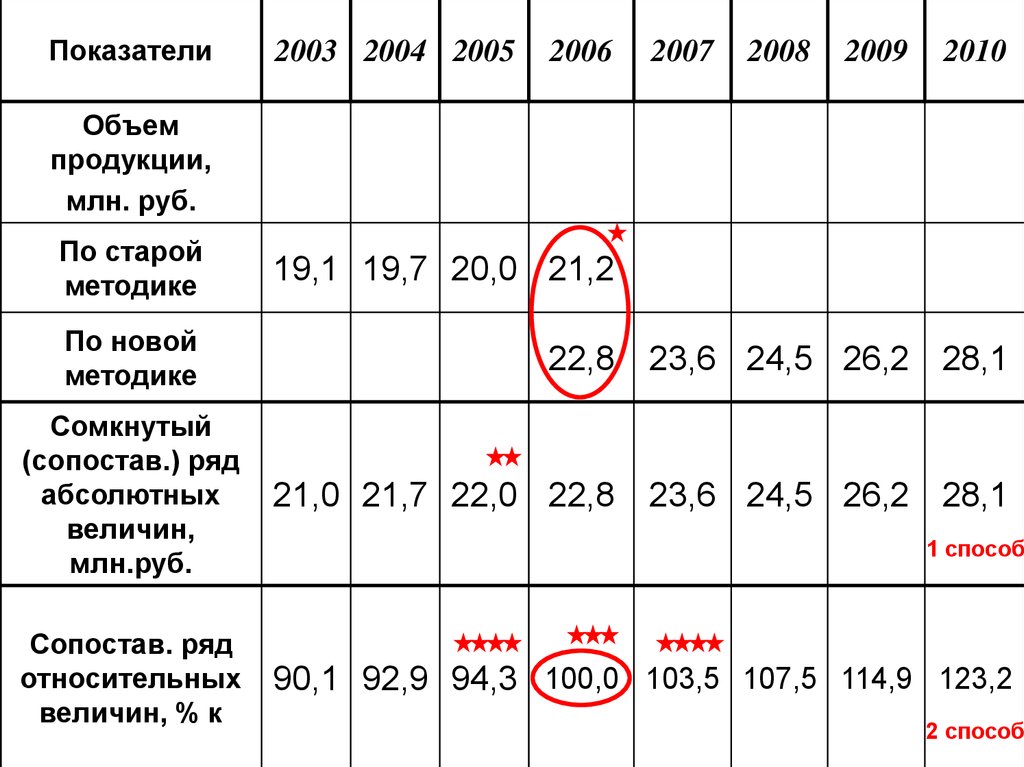
Показатели2003 2004 2005
2006
2007
2008
2009
2010
Объем
продукции,
млн. руб.
По старой
методике
19,1 19,7 20,0 21,2
По новой
методике
22,8
23,6 24,5 26,2 28,1
Сомкнутый
(сопостав.) ряд
абсолютных
величин,
млн.руб.
21,0 21,7 22,0 22,8
23,6 24,5 26,2 28,1
Сопостав. ряд
относительных
величин, % к
90,1 92,9 94,3 100,0 103,5 107,5 114,9 123,2
1 способ
2 способ
3.
22,8 21,2 1,122,0 20,0 1,1
21,2 100%
22,8 100%
21,2 100%
20,0 x%
20,0 100
x
21,2
x 94,3%
22,8 100%
23,6 x%
23,6 100
x
22,8
x 103,5%
4.
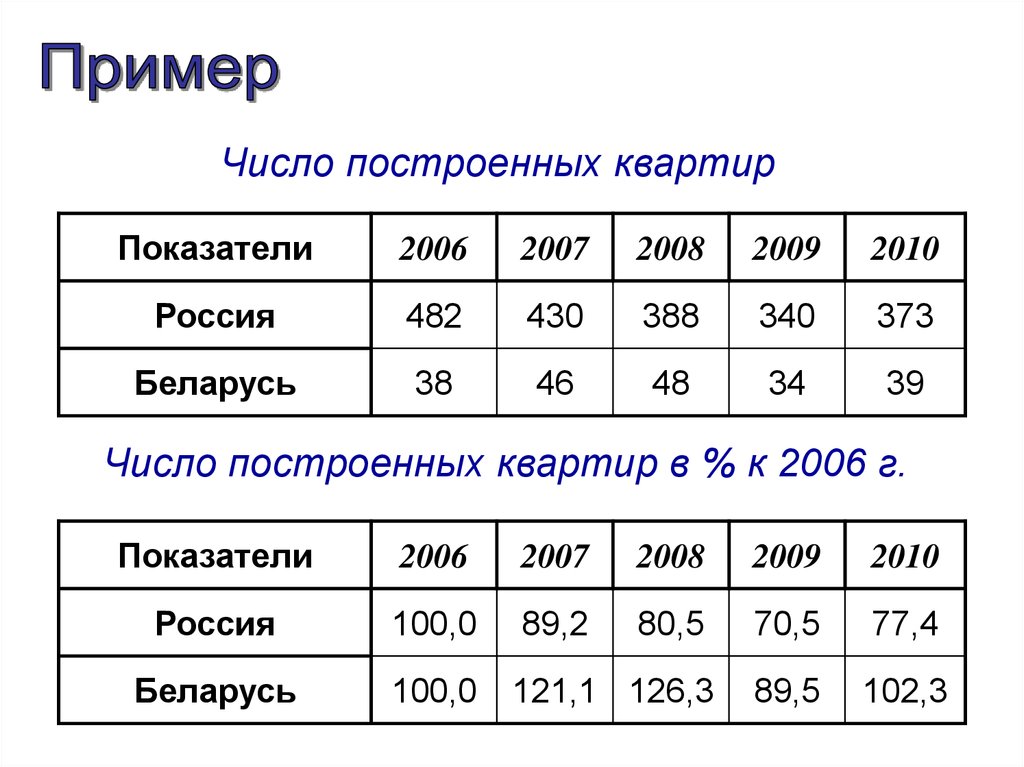
Число построенных квартирПоказатели
2006
2007
2008
2009
2010
Россия
482
430
388
340
373
Беларусь
38
46
48
34
39
Число построенных квартир в % к 2006 г.
Показатели
2006
2007
2008
2009
2010
Россия
100,0
89,2
80,5
70,5
77,4
Беларусь
100,0
121,1 126,3
89,5
102,3
5.
kОТ2
Т1
kО
Т1
Т2
kО
Т2
Т1
kО
Т1
Т2
, где T2 T1 Применяется, когда ряд
представляет
, где T1 T2 постоянное повышение
Применяется, когда
нет ярко-выраженной
тенденции к росту
6.
Средние темпы роста для Белоруссии – 100,33%,для России – 96,41%
kО
1,033
1,04
0,9641
В 2010г. по сравнению с 2006г. число построенных
квартир в Белоруссии было в 1,04 раза больше, чем в
России
7.
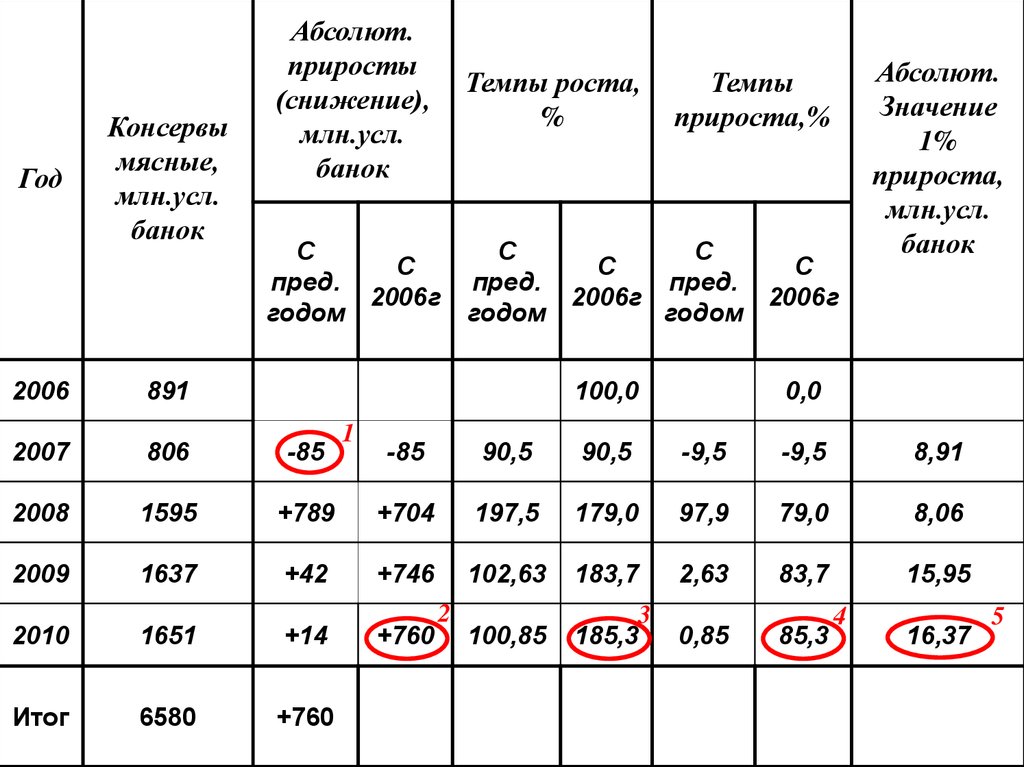
Год2006
Консервы
мясные,
млн.усл.
банок
Абсолют.
приросты
(снижение),
млн.усл.
банок
Темпы роста,
%
С
С
пред.
2006г
годом
Темпы
прироста,%
С
С
С
С
пред.
пред.
2006г
2006г
годом
годом
891
100,0
2007
806
-85
2008
1595
2009
1637
1
Абсолют.
Значение
1%
прироста,
млн.усл.
банок
0,0
-85
90,5
90,5
-9,5
-9,5
8,91
+789
+704
197,5
179,0
97,9
79,0
8,06
+42
+746
102,63
183,7
2,63
83,7
15,95
100,85
3
185,3
2010
1651
+14
Итог
6580
+760
+760
2
0,85
85,3
4
16,37
5
8.
ц y i y i 1или
б yi y1
yi – уровень i-ого года
y1 – уровень базисного года
1 806 891 85 млн. услов. банок
2 1651 891 760 млн. услов. банок
9.
yiр
100
y i 1
3
или
yi
р
100
y1
1651
100 185,3%
891
10.
пр100
y i 1
Также:
или
пр
100
y1
пр р 100
Может быть: положительным, отрицательным, равным 0
4 760
891
100 85,3% или 185,3 100 85,3%
11.
%пр
или
% 0,01 y i 1
Показывает, сколько
абсолютных единиц приходится
на 1 % прироста (уменьшения)
5
0,01 1637 16,37% или
14
16,37 млн. услов. банок
0,85
12.
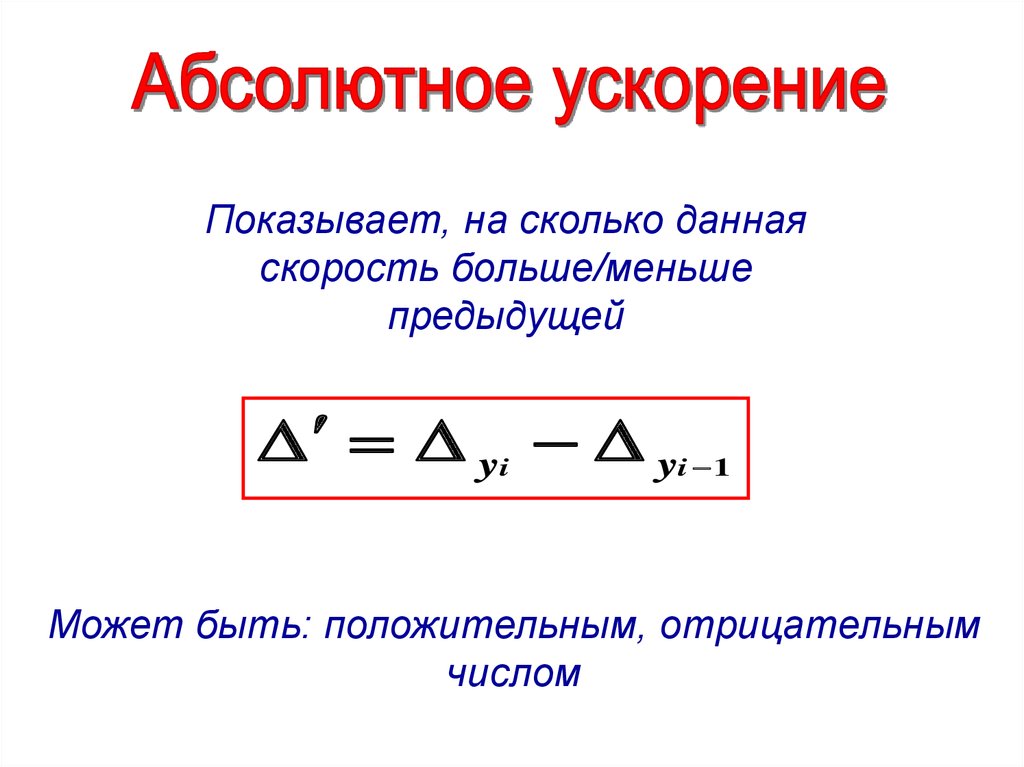
Показывает, на сколько даннаяскорость больше/меньше
предыдущей
yi yi 1
Может быть: положительным, отрицательным
числом
13.
yiТемп прироста
абсолютного прироста
14.
Для ряда: 30, 33, 35, 39, 44Абсолютные приросты: 3, 2, 4, 5
Абсолютные ускорения: –1, 2, 1
Относительные ускорения: (–1/3)*100%= –33,3%
(2/2)*100%= 100%
(1/4)*100%= 25%
15.
1)Для интервальных рядов сравноотстоящими уровнями
n
y
y
i 1
i
n
yi – уровень ряда динамики
n – число наблюдений
16.
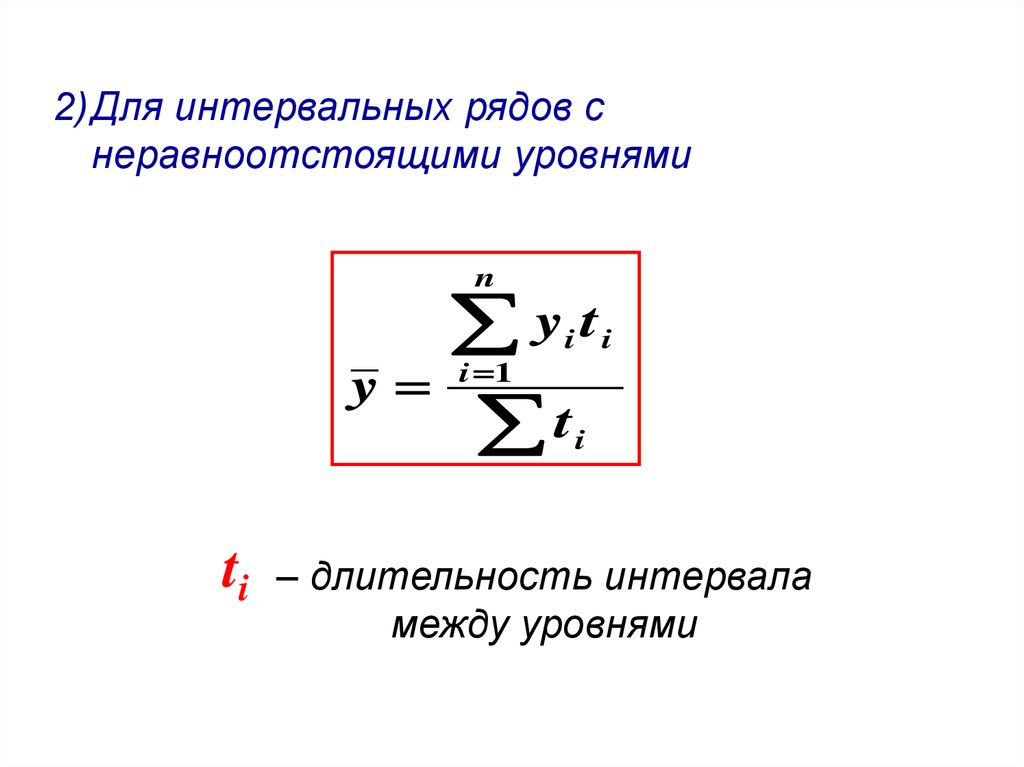
2)Для интервальных рядов снеравноотстоящими уровнями
n
yt
y
t
i 1
i i
i
ti
– длительность интервала
между уровнями
17.
3)Для моментного ряда сравноотстоящими уровнями
y n 1 y n 1
y1 y2 y2 y3
1
...
y1 y2 ... yn
2
2
2
y 2
2
n 1
n 1
или
y1 y n n 1
yi
2
i 2
y
n 1
18.
4)Для моментного ряда снеравноотстоящими уровнями
y
y1 y2 t1 y2 y3 t 2 ... yn 1 yn t n 1
2
2
2 ( t1 t 2 ... t n -1 )
или
y
y
i
y i 1 t1
2 t i
yi , yn
– уровни рядов динамики
2
19.
Известны товарные остатки магазина на1ое число каждого месяца, тыс.руб.:
1 января
1 февраля
1 марта
1 апреля
18
14
16
20
1 способ:
18
20
14 16
49
2
2
y
16,3 тыс.руб.
3
3
20.
2 способ:Предполагается непрерывное,
равномерное изменение уровня в
промежутках между 2мя датами
18
14
январь
16
2
14 16
февраль
15
2
16 20
март
18
2
16 15 18
y
16 ,3 тыс.руб.
3
21.
Известна списочная численность рабочихорганизаций на некоторые даты 2008г., чел.:
1 января
1 марта
1 июня
1 сентября
1 января
2009
1200
1100
1250
1500
1350
1200 1100 2 1100 1250 3
y
2 ( 2 3 3 4)
1250 1500 3 1500 1350 4
31300
1304 чел.
24
22.
yц
n -1
или
yn y1
y
n -1
Возможен расчет, исходя из кумулятивных данных:
n
2 yn ny1
i 1
y
n n 1
23.
Среднегодовой прирост продажи мясныхконсервов за 2006-2010гг.
760
190 млн. услов. банок
4
или
1651 891
190 млн. услов. банок
4
24.
P y m k 2 1 k 3 2 ... k n n 1или
P y n 1
yn
y1
m – число коэффициентов роста
25.
Средний темп роста продажи мясныхконсервов за 2006-2010гг.
P 4 0,905 1,979 1,0263 1,0085
4 1,853 1,167 116,7%
или
1651 4
P
1,853 1,167 116,7%
891
4
26.
При разноотстоящих рядах используется:P
t
t
t
(k2 1 ) (k3 2 ) ... (kn n 1 )
t1
t2
– интервал, в течении которого
сохраняется данный темп роста
– сумма отрезков периода
tn
27.
Получается уменьшением среднего темпароста на 1 или 100%
пр р 100
28.
Средний темп прироста продажи мясныхконсервов за 2006-2010гг.
пр 116,7 100 16,7%
29.
1)Метод проверки существенностиразности средних
H 0 : y1 y2
2)Метод Фостера-Стюарта
30.
1)Сравнивается каждый уровень ряда совсеми предыдущими, при этом:
если
то
если
то
yi yi 1 ; yi 2 ;...; y1
ui 1; l i 0
yi yi 1 ; yi 2 ;...; y1
u i 0; li 1
31.
2)Вычисляются значения величин S и d:S Si
d di
Si U i li
d i U i li
Характеризует
тенденцию изменения
дисперсии ряда
Характеризует
изменение тенденций
в среднем
32.
3)Проверяется с использованием t-критерияСтьюдента гипотеза о том, можно ли
считать случайными разности S-M и d-0:
ts
M
S M
1
td
d 0
2
– среднее значение величины S, определенное для ряда,
в котором уровни расположены случайным образом
1 и 2
– стандартные ошибки величин S и d
соответственно
33.
4)Сравниваются расчетные значения ts и td стабличными при заданном уровне
значимости
t s t табл.
t d t табл.
Гипотеза об отсутствии
тренда в средней и
дисперсии подтверждается
34.
Год1991
1992
1993
1994
1995
1996
1997
1998
млн.руб.
(yi)
ui
63,5
0
62,1
61,6
61,3
61,5
61,3
62,4
65,5
0
0
0
0
0
0
1
li
0
1
1
1
0
0
0
0
1999
64,8
0
0
2000
64,3
0
0
2001
63,0
0
0
2002
59,9
0
1
2003
62,0
0
0
2004
63,4
0
0
2005
64,5
0
0
2006
58,0
0
0
2007
54,5
0
1
2008
56,0
0
1
2009
55,2
0
0
2010
56,1
0
0
1
6
35.
1(0 S n 1)
S 7
2
n 20
( ( n 1) d n 1)
d 5
M 5,195
1 1,677
2 2,279
3
7 5,195
ts
1,076
1,677
n 20
5 0
td
2,194
2,279
уровень значимости – 0,10
4 t табл. 1,725 t s 1,076
t d 2,194
36.
•Метод усреднения по левой иправой половине
•Метод укрупнения интервалов
•Метод скользящей средней
37.
1) Определить интервал сглаживания,т.е. число входящих в него уравнений m
(m<n) по правилу:
Если необходимо сгладить мелкие,
беспорядочные колебания, то
интервал сглаживания берут большим
(и наоборот)
38.
2) Вычислить среднее значение уравнений,образующих интервал сглаживания:
t p
yt
или
y
i t p
m
y t y t 1
y t p y t p 1
m
39.
yi – фактическое значение i-ого уровняyt – текущий уровень ряда динамики
m – число уровней, входящих в интервал
сглаживания (m=2p+1)
i – порядковый номер уровня в интервале
сглаживания
p – при нечетной m равно: p=(m-1)/2
40.
3) Сдвинуть интервал сглаживания на 1точку вправо, вычислить сглаженное
значение для t+1 члена, снова произвести
сдвиг и т.д.
В результате получится n-(m-1)
новых сглаженных уровней
41.
4хчленСтиральные
скольз.
Мес. машины, скольз. скольз. скольз. средние (не
тыс.шт.
суммы средние суммы
централ.)
3хчлен.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
155
163
167
131
158
147
130
145
128
140
159
100
147
150
165
4851
461
456
436
435
422
403
413
427
459
466
457
462
3хчлен.
161,72
153,7
152,0
145,3
145,0
140,7
134,3
137,7
142,3
153,0
155,3
152,3
154,0
4хчлен
6163
619
603
566
580
550
643
672
687
606
616
622
154,04
154,8
150,8
141,5
145,0
137,5
135,8
143,0
146,8
151,5
154,0
155,5
4хчлен
скольз.
средние
(централ.)
154,45
152,8
146,2
143,3
141,3
136,7
139,4
144,9
149,2
152,8
154,8
42.
1155 163 167 485
2 485
3
3
155 163 167 131 616
4 616
4
5
161,7
154
154 154,8
154,4
2
43.
Динамика производства готовой продукциина фирме
2005
2006
2007 2008 2009 2010
Готовая
продукция
фирмы, тыс.руб.
18
21
26
22
25
28
t
1
2
3
4
5
6
44.
Приняв условные обозначения временичерез t и взяв 2 точки – конечный и
начальный уровни, можно построить
уравнение прямой по этим 2м точкам;
yt a0 a1t
2005 :
2010 :
a0 1 a1 18
a0 6 a1 28
yt 16 2t
a1 2
a 0 16
45.
Развитие по параболе 2-ого порядка:yt a0 a1 t a 2 t
2005 : t 1
2008 : t 4
2010 : t 6
2
a0 1 a1 1 a2 18
a0 4 a1 16 a2 22
a 6 a 36 a 28
1
2
0
a0 18
a1 0,3
a 2 0,3
yt 18 0,3t 0,3t 2
46.
47.
Вычисляем 1ые разности:yt 1 yt
2ые разности:
(1)
t
( 2)
t
(1)
t 1
(1)
1
Окончательная формула
для расчета уровней ряда
при равных или почти равных 1ых разностях:
yt y t
( 1)
1
48.
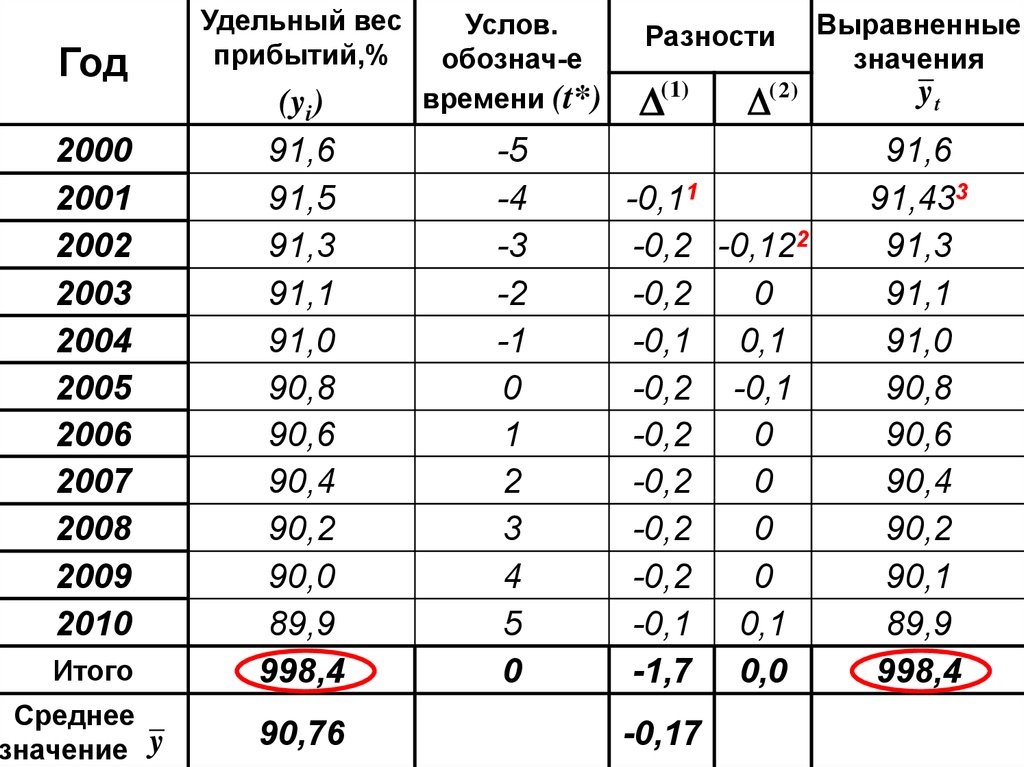
Удельный весприбытий,%
Год
(yi)
91,6
91,5
91,3
91,1
91,0
90,8
90,6
90,4
90,2
90,0
89,9
998,4
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
Итого
Среднее
значение
y
90,76
Услов.
обознач-е
времени (t*)
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
Разности
(1)
( 2 )
-0,11
-0,2 -0,122
-0,2
0
-0,1 0,1
-0,2 -0,1
-0,2
0
-0,2
0
-0,2
0
-0,2
0
-0,1 0,1
-1,7 0,0
-0,17
Выравненные
значения
yt
91,6
91,433
91,3
91,1
91,0
90,8
90,6
90,4
90,2
90,1
89,9
998,4
49.
10,1 91,5 91,6
2
0,1 0,2 ( 0,1)
3
91,4 90,76 ( 0,17) ( 4)
yt 90,76 0,17t
50.
51.
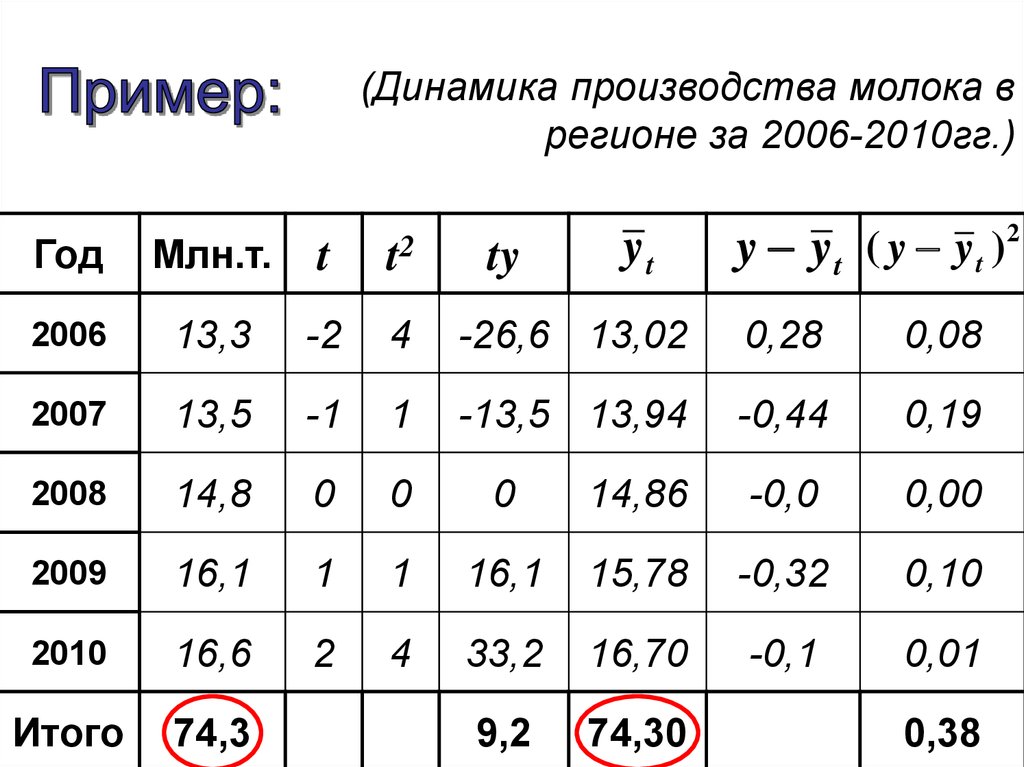
(Динамика производства молока врегионе за 2006-2010гг.)
yt
y yt ( y yt )
Год
Млн.т.
t
t2
2006
13,3
-2
4
-26,6 13,02
0,28
0,08
2007
13,5
-1
1
-13,5 13,94
-0,44
0,19
2008
14,8
0
0
0
14,86
-0,0
0,00
2009
16,1
1
1
16,1
15,78
-0,32
0,10
2010
16,6
2
4
33,2
16,70
-0,1
0,01
Итого
74,3
9,2
74,30
ty
0,38
2
52.
Уравнение прямой:yt a0 a1t
Система нормальных уравнений по способу
наименьших квадратов:
a0 n a1 t y
2
a
t
a
t
ty
0
1
t 0
a 0 n y
2
a1 t ty
n 5
53.
y 74,3a0
14,86
n
5
y
- средний уровень ряда
ty 9,2
a1
0,92
2
10
t
yt 14,86 0,92t
2006:
y1 14,86 0,92 ( 2) 13,02
2007:
y2 14,86 0,92 ( 1) 13,94
54.
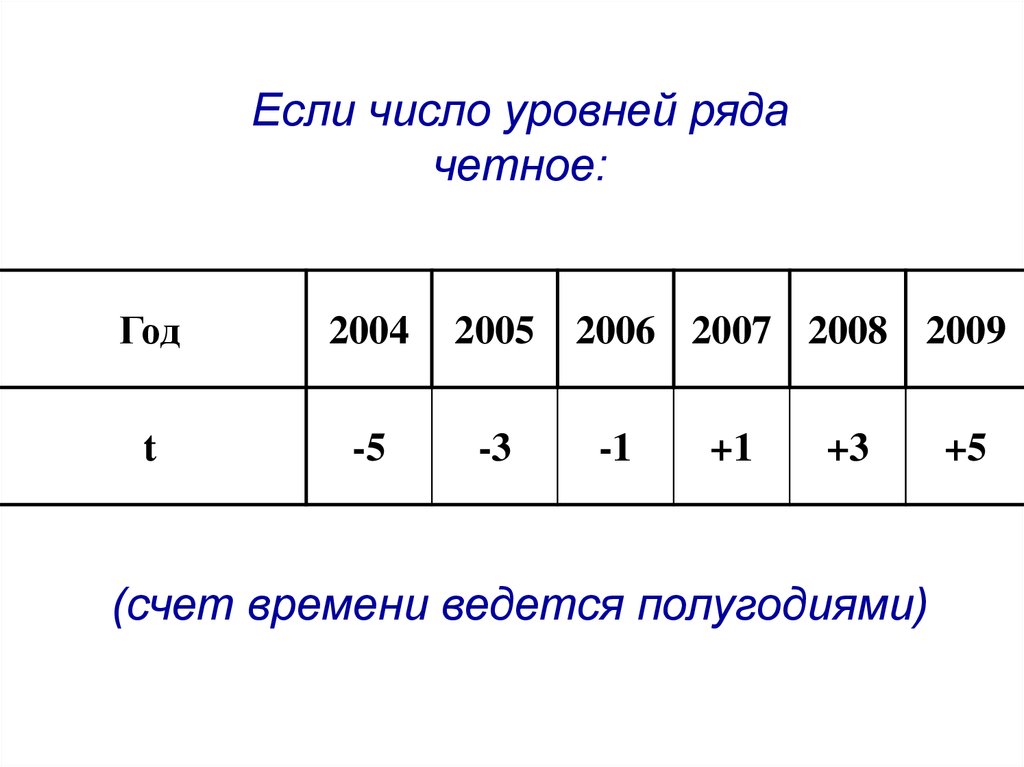
Если число уровней рядачетное:
Год
2004
2005
t
-5
-3
2006 2007 2008 2009
-1
+1
+3
(счет времени ведется полугодиями)
+5
55.
Служит мерой воздействияостаточных факторов
t
( y yt )
n
2
56.
(Показатель колеблемостипроизводства молока в регионе)
0,38
t
0,076 0,275
5
млн.т.
57.
Является относительноймерой колеблемости
t
y
58.
(Относительный показательколеблемости производства
молока в регионе)
0,275
0,0185 1,85%
14,86
59.
60.
myt a0 (ak cos kt bk sin kt )
t 0
k – степень точности гармоники
тригонометрического многочлена
t – время
•выражается в радиальной мере
•определяется от 0 с приростом 2П/n
(n – число уравнений ряда)
61.
По методу наименьших квадратов:1
a0 y
n
2
a k y cos kt
n
2
bk y sin kt
n
62.
Для изучения сезонности n=12(по числу месяцев в году)
2
12 6
4
12 3
6
12 2
8 2
12
3
10 5
12
6
12
12
14
12
16
12
18
12
20
12
22
12
7
6
4
3
3
2
5
3
11
6
63.
Мес.Продано,т
t
y
1
30
1
0
30,0
0
35,60
2
40
0,866
0,5
34,64
20,0
40,51
3
43
0,5
0,866
21,5
37,24
45,11
4
54
0
1
0
54,00
48,03
5
67
-0,5
0,866
-33,5
58,02
48,55
6
29
-0,866
0,5
-25,11
14,5
46,53
7
35
-1
0
-35,00
0
42,52
8
34
-0,866
-0,5
-29,44
-17,00
38,25
9
45
-0,5
-0,866
-22,50
-38,97
33,05
10
35
0
-1
0
-35,00
30,13
11
29
0,5
-0,866
14,50
-25,11
29,61
12
28
24,25
-14,00
31,63
Итого
469
-20,66
53,68
469,52
Cos(t)
Sin(t) yCos(t) ySin(t)
0,866
-0,5
По таблице
yt
64.
k 1yt a0 a1 cos t b1 sin t
469
a0
39,8
12
2 ( 20,66)
ak
3,44
12
2 53,68
bk
8,95
12
yt 39,08 3,44 cos t 8,95 sin t
65.
35,60 39,08 3,44 1 8,95 040,51 39,08 3,44 0,866 8,95 0,5
39,08 2,97904 4,475
45,11 39,08 3,44 0,5 8,95 0,866
39,08 1,72 7,7507
66.
Аналогично рассчитываютсягармоники 2-ого и высших порядков
k 2
yt a0 a1 cos t b1 sin t a2 cos 2t b2 sin 2t
2 y cos 2t
a2
n
2 y sin 2t
b2
n
67.
Рассчитав остаточные дисперсии длявсех гармоник,
2
ост .
( y yt )
n
2
можно сделать вывод, какая гармоника
ряда Фурье наиболее близка к
фактическим уровням ряда.
68.
69.
yiI S 100%
y
yi
– средняя величина уровня
y
– среднемесячный
уровень для всего ряда
70.
МесяцЯнварь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Число расторженных браков
2008
2009
2010
195
164
153
136
136
123
126
121
118
126
129
138
158
141
153
140
136
129
128
122
118
130
131
141
144
136
146
132
136
125
124
119
118
128
135
139
135,6
131,8
Средний уровень
ряда
( y ) 138,77
В среднем за 3 I yi 100%
S
y
года ( y i )
165,71
147,02
150,7
136,0
136,0
125,7
126,0
120,7
118,0
128,0
131,7
139,3
1624,8
135,43
122,44
108,65
111,3
100,4
100,4
92,8
93,1
89,1
87,2
94,5
97,3
102,9
100,0
71.
1195 158 144 497
y1
165,7
3
3
2
164 141 136 441
y2
147,0
3
3
3
yi 1624,8
y
135,4
n
12
или
( yi ) 138,77 135,6 131,8 406,1
y
135,4
m
3
3
m - число лет
72.
4янв.: I S1
165,7
100% 122,4%
135,4
5
февр.:
I S2
147,0
100% 108,6%
135,4
73.
1) Вычислить для каждого месяца(квартала) выравненные уровни по
соответствующему аналитическому
уровню на момент времени t
74.
2) Определить отклонения фактическихмесячных (квартальных) данных к
соответствующим выравненным
данным в %:
yi
I i 100%
yt
75.
3) Найти среднее арифметическое изпроцентных соотношений, рассчитанных
по одноименным периодам в %
I1 I 2 I 3 ... I n
Ii
n
n – число одноименных периодов
76.
4) Из полученных величин ( Ii ) вычислить общийсреднемесячный уровень ( It )
5) Определить индексы сезонности по
формуле:
Ii
I S 100%
It
или
I S [
yi
]: n
yt
77.
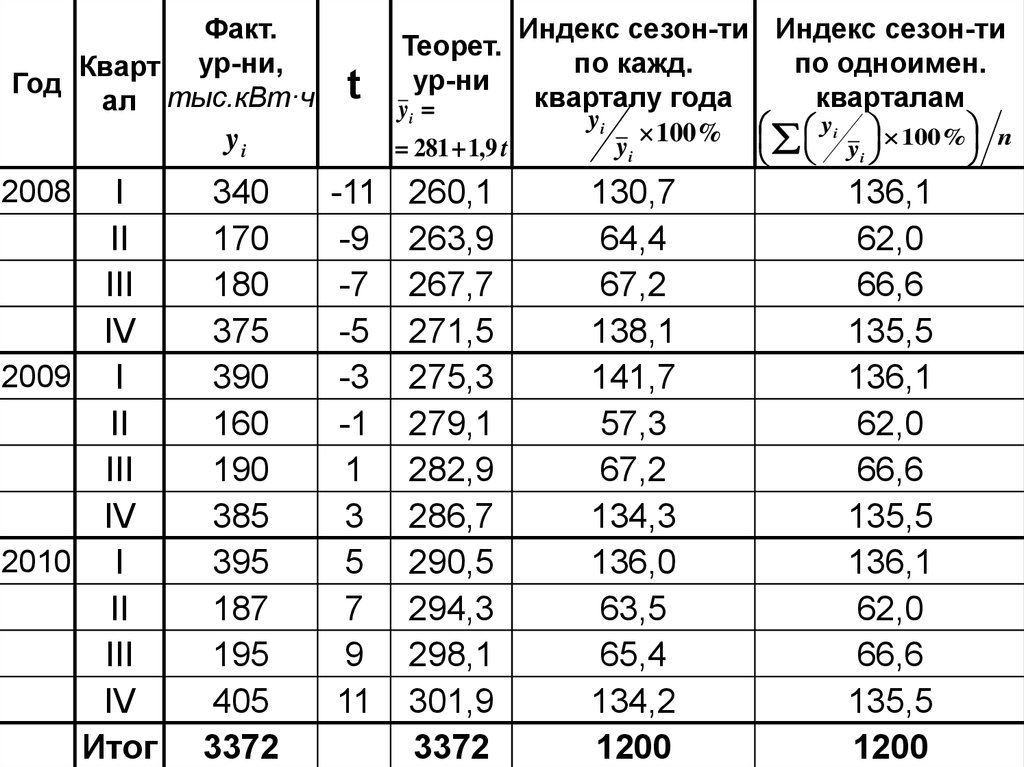
Факт.Кварт ур-ни,
Год
ал тыс.кВт·ч
t
yi
I
II
III
IV
2009 I
II
III
IV
2010 I
II
III
IV
Итог
2008
340
170
180
375
390
160
190
385
395
187
195
405
3372
Теорет.
ур-ни
yi
281 1,9 t
-11
-9
-7
-5
-3
-1
1
3
5
7
9
11
260,1
263,9
267,7
271,5
275,3
279,1
282,9
286,7
290,5
294,3
298,1
301,9
3372
Индекс сезон-ти Индекс сезон-ти
по кажд.
по одноимен.
кварталу года
кварталам
yi
yi
100%
130,7
64,4
67,2
138,1
141,7
57,3
67,2
134,3
136,0
63,5
65,4
134,2
1200
yi
y 100% n
i
136,1
62,0
66,6
135,5
136,1
62,0
66,6
135,5
136,1
62,0
66,6
135,5
1200
78.
130,7 141,7 136,0I: 136,1
3
64,4 57,3 63,5
II: 62,0
3
Проверка:
136,1 62,0 66,6 135,5
100%
4
136,1 62,0 66,6 135,5 3 400 3 1200
79.
%140
120
100
80
60
40
I
II
III
IV
квартал
80.
Измеряется с помощьюнециклического коэффициента
автокорреляции
yt yt 1 yt yt 1
ra
yt yt 1
81.
Если yn = y1, то yt = yt+1 ; yt yt 1yt yt 1 yt
2
ra
2
yt
или
y y n y
y n y
2
ra
t 1
t
2
t
t
2
t
82.
Если y = 0n 1
ra
y
t 1
t
yt 1
n
y
t 1
2
t
83.
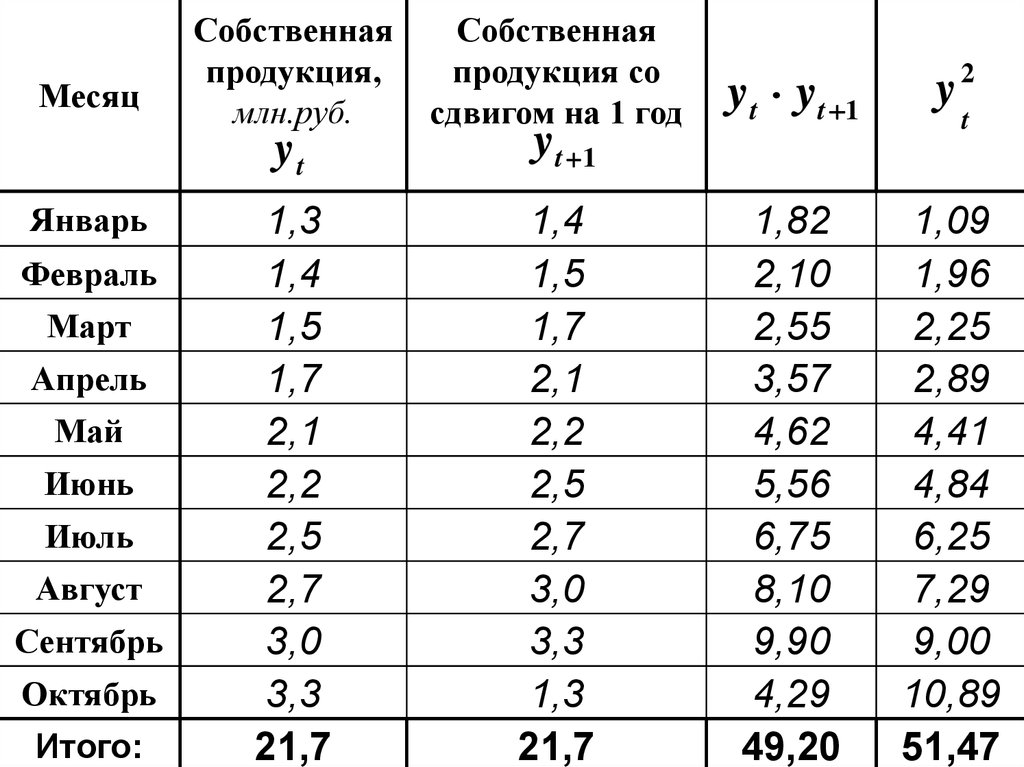
МесяцЯнварь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Итого:
Собственная
продукция,
млн.руб.
Собственная
продукция со
сдвигом на 1 год
y
yt
yt 1
yt yt 1
1,3
1,4
1,5
1,7
2,1
2,2
2,5
2,7
3,0
3,3
21,7
1,4
1,5
1,7
2,1
2,2
2,5
2,7
3,0
3,3
1,3
21,7
1,82
2,10
2,55
3,57
4,62
5,56
6,75
8,10
9,90
4,29
49,20
1,09
1,96
2,25
2,89
4,41
4,84
6,25
7,29
9,00
10,89
51,47
2
t
84.
yt yt 1y
yt
y
yt
2
t
yt 1
n
t
n
2
y
t
49,20
4,92
10
21,7
2,17
10
2,17 4,71
2
y
n
2
t
51,47
5,15
10
y yt 5,15 4,71 0,44
2
y1
2
t
2
85.
4,92 4,71ra
0,48
0,44
n=10 p=0,05 ra=0,36
По «Таблице 5%-ого и 1%-ого уравнений
вероятности коэффициентов корреляции»
0,48 > 0,36
Наличие автокорреляции
86.
87.
nd
l
t 1
lt
2
t 1
n
l
2
t
1
l t yt yt
88.
d 22 d 4
d 0;4
Автокорреляция
положительная
Автокорреляция
отрицательная
Всегда ближе к 2 (при
условии, что
отклонения уровней от
тенденции, остатки,
случайны)
89.
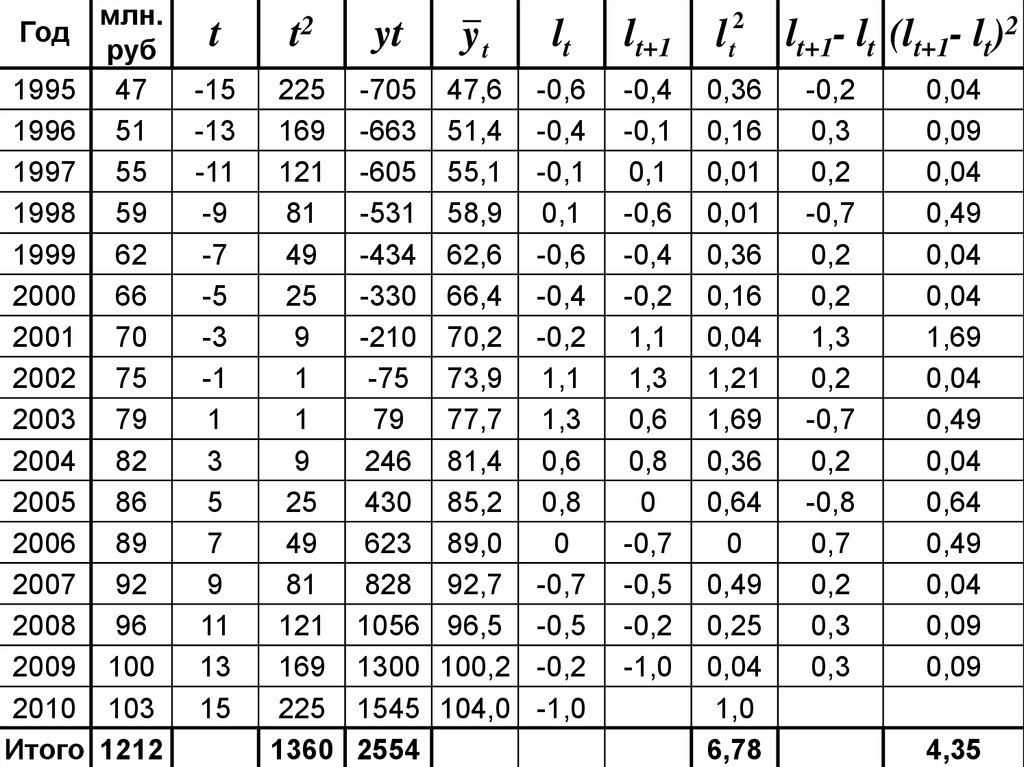
Год1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
Итого
млн.
руб
47
51
55
59
62
66
70
75
79
82
86
89
92
96
100
103
1212
t
t2
yt
yt
lt
lt+1
l t2
-15
-13
-11
-9
-7
-5
-3
-1
1
3
5
7
9
11
13
15
225
169
121
81
49
25
9
1
1
9
25
49
81
121
169
225
1360
-705
-663
-605
-531
-434
-330
-210
-75
79
246
430
623
828
1056
1300
1545
2554
47,6
51,4
55,1
58,9
62,6
66,4
70,2
73,9
77,7
81,4
85,2
89,0
92,7
96,5
100,2
104,0
-0,6
-0,4
-0,1
0,1
-0,6
-0,4
-0,2
1,1
1,3
0,6
0,8
0
-0,7
-0,5
-0,2
-1,0
-0,4
-0,1
0,1
-0,6
-0,4
-0,2
1,1
1,3
0,6
0,8
0
-0,7
-0,5
-0,2
-1,0
0,36
0,16
0,01
0,01
0,36
0,16
0,04
1,21
1,69
0,36
0,64
0
0,49
0,25
0,04
1,0
6,78
lt+1- lt (lt+1- lt)2
-0,2
0,3
0,2
-0,7
0,2
0,2
1,3
0,2
-0,7
0,2
-0,8
0,7
0,2
0,3
0,3
0,04
0,09
0,04
0,49
0,04
0,04
1,69
0,04
0,49
0,04
0,64
0,49
0,04
0,09
0,09
4,35
90.
y t a 0 a1 tna 0 y
a1 t 2 ty
16a0 1212
1360a1 2554
a0 75,8
a1 1,88
yt 75,8 1,88t
4,35
d
0,64 2 - Положительная
6,78
автокорреляция
91.
92.
Ликвид. Собств.активы капитал
млрд.
Год млрд.
руб.
руб
t
xy
x2
ty
t2
tx
y xt
x
y
2002
9
27
1
243
81
27
1
9
30,5
2003
13
36
2
468
169
72
4
26
32,4
2004
17
29
3
493
289
87
9
51
34,2
2005
22
41
4
902
484
164
16
88
38,7
2006
29
54
5
1566
841
270
25
145
48,3
2007
36
71
6
2566 1296
426
36
216
58,0
2008
44
50
7
2200 1936
350
49
308
70,3
2009
51
81
8
4131 2601
648
64
408
79,9
2010
60
98
9
5880 3600
882
81
540
94,8
Итог
281
487
45
18439
2926
285
1791
487,1
11297
93.
na0 a1 x a2 t y2
a
x
a
x
a2 xt yx
0
1
2
a
t
a
xt
a
t
yt
1
2
0
9a0 281a1 45a2 487
281a0 11297a1 1791a2 18439
45a 1791a 285a 2926
0
1
2
a0 15,63
a1 2,61
a 8,60
2
y xt 15,63 2,61 8,6t
94.
x y x yr
x y
95.
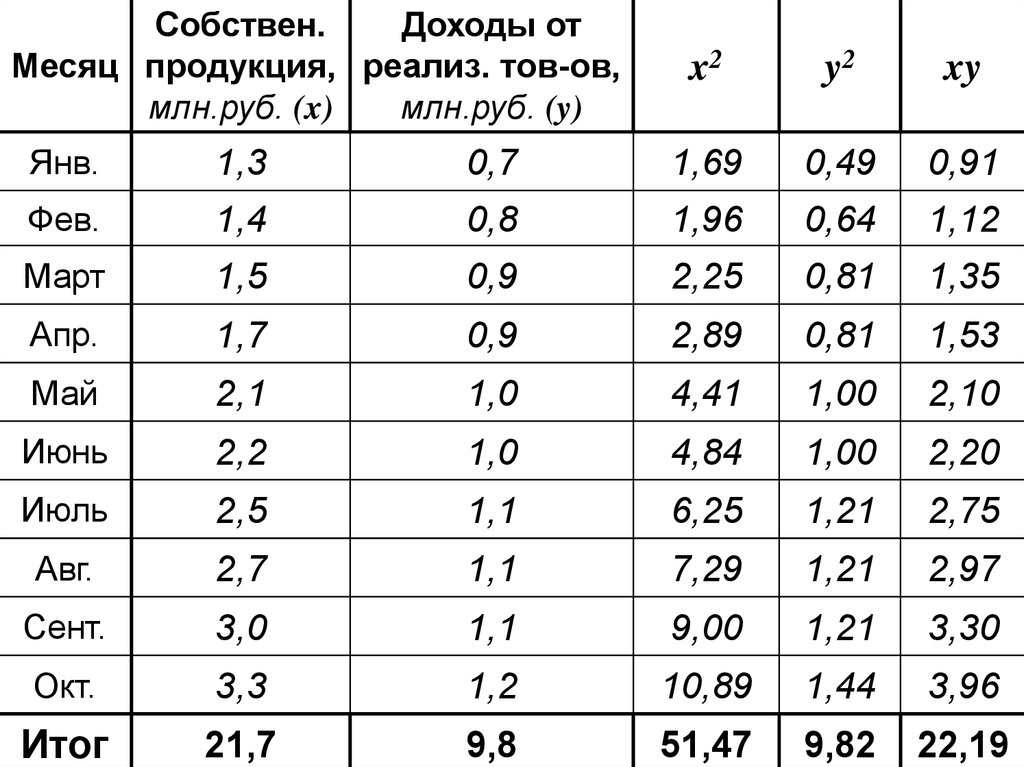
Собствен.Доходы от
Месяц продукция, реализ. тов-ов,
млн.руб. (x)
млн.руб. (y)
x2
y2
xy
Янв.
1,3
0,7
1,69
0,49
0,91
Фев.
1,4
0,8
1,96
0,64
1,12
Март
1,5
0,9
2,25
0,81
1,35
Апр.
1,7
0,9
2,89
0,81
1,53
Май
2,1
1,0
4,41
1,00
2,10
Июнь
2,2
1,0
4,84
1,00
2,20
Июль
2,5
1,1
6,25
1,21
2,75
Авг.
2,7
1,1
7,29
1,21
2,97
Сент.
3,0
1,1
9,00
1,21
3,30
Окт.
3,3
1,2
10,89
1,44
3,96
Итог
21,7
9,8
51,47
9,82
22,19
96.
x 2,17y 0,98
xy 2,22
0,436
2
x
2,22 2,13
r
0,02 0,44
0,09
0,09
0,96
0,0088 0,094
0,02
2
y
x y 2,13
Связь прямая сильная
97.
98.
1) Каждый ряд динамики выравнивают поопределенной, характерной для него
аналитической формуле
2) Из эмпирических уравнений вычитают
выравненные:
d x xt xt
d y yt yt
99.
3) Определяют тесноту связи междурассчитанными отклонениями (dx и dy)
по формуле:
rd x d y
d d
d d
x
2
x
y
2
y
100.
101.
r x yx
2
x
x x i x i 1
y y i y i 1
y
2
y
102.
rat
2
t
t 1
t yi yt
t 1 yi yt 1
103.
yˆ i T f yi , T , a jyˆ i T - прогнозируемый уровень
y i - текущий уровень
прогнозируемого ряда
T -период упреждения
(срок экстраполяции)
aj
- параметр уровня тренда
104.
yˆ i t yi t105.
yˆ i t - экстраполяционный уровень( i t ) - номер этого уровня (года)
i - номер последнего уровня (года),
исследуемого периода, за который
рассчитан
t
- срок прогноза
- средний абсолютный прирост
106.
Использование среднего абсолютногоприроста возможно только при
следующем условии:
2
ост.
p
2
1
2
p
; ост.
2 n
2
2
i
y
y
2
i
n
107.
По данным об удельном весе прибытиявоздушных судов, выполненных без опоздания
по сравнению с расписанием за 2000-2010гг.
экстраполируем ряд на 2011-2012гг.
yˆ 2011 89,9 ( 0,17) 89,7%
yˆ 2012 89,7 ( 0,17) 89,5%
108.
yˆ i t yi kt
p
y i - последний уровень ряда
k
t
- срок прогноза
t
p
- средний коэффициент роста
109.
n myˆ t t yt
m
- число
параметров
адекватной
модели
тренда
110.
yˆ ty
t
t
- расчетное значение уровня
- средняя квадратичная ошибка тренда
- доверительная величина по
распределению Стьюдента
(t-распределение)
























































































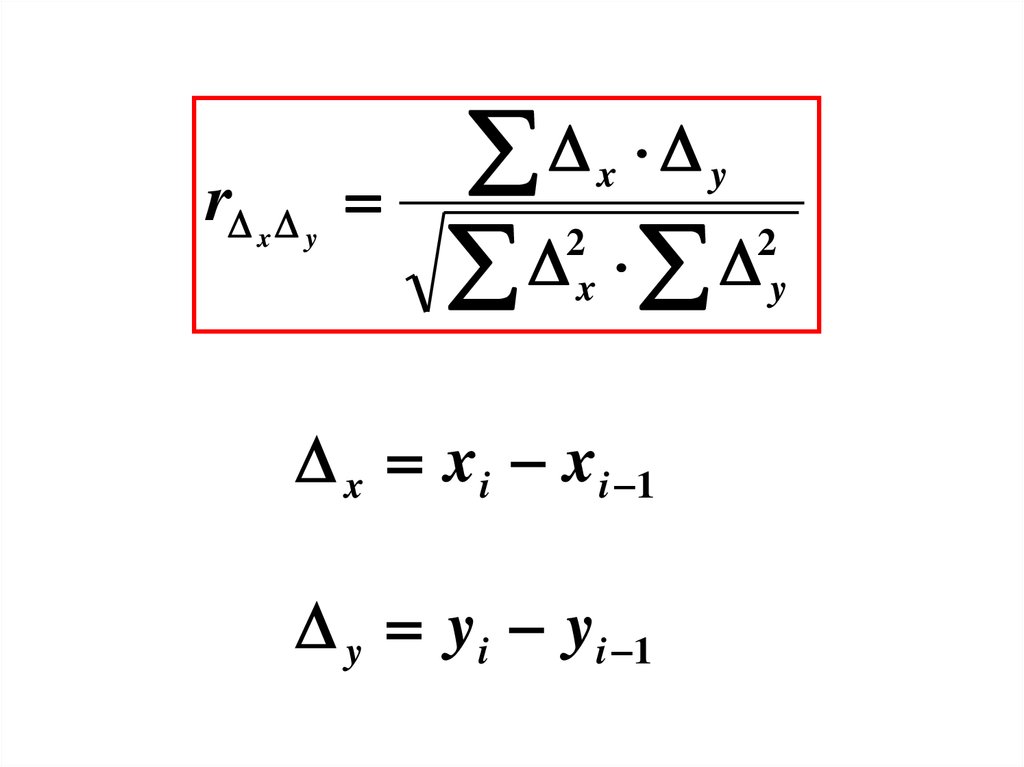









 Математика
Математика








