Похожие презентации:
Статистика. Статистическое исследование
1. Статистика
2.
• statys (лат.) – состояние• statu (итал.) – государство
• statistu – знаток государства.
3.
Как предмет статистика имеет 3 отличительных
особенности:
1. статистика изучает количественную сторону
общественных явлений и процессов в конкретных
условиях места и времени;
2. статистика изучает количественную сторону
массовых явлений общественной жизни, т.е.
совокупностей, состоящих из большого числа
отдельных единиц;
3. изучаемые статистикой совокупности
общественных явлений имеют 2 характерные черты:
- качественная однородность единиц;
- варьирование изучаемых признаков.
4.
Любое статистическое исследованиесодержит 3 стадии:
• 1. статистическое наблюдение;
• 2. сводка материалов статистического
наблюдения;
• 3. анализ.
5. .
53
4
5
3
4
3
4
5
3
4
3
3
3
4
4
5
3
4
4
4
3
4
5
3
5
4
4
3
4
4
4
5
3
5
4
6.
34
5
12
16
8
7.
x3
4
5
f
12
16
8
f = n =36
f
f/
частота
частость
f/
12/36
16/36
8/36
f/ = 1 (100%)
8.
группачисленность
младенцы
4
дошкольники
24
школьники
94
молодежь
80
ср. возраст
378
пенсионеры
70
f
650
9.
группачисленность
до 1
4
1–7
24
7 – 17
94
17 – 25
80
25 – 58
378
старше 58
70
f
650
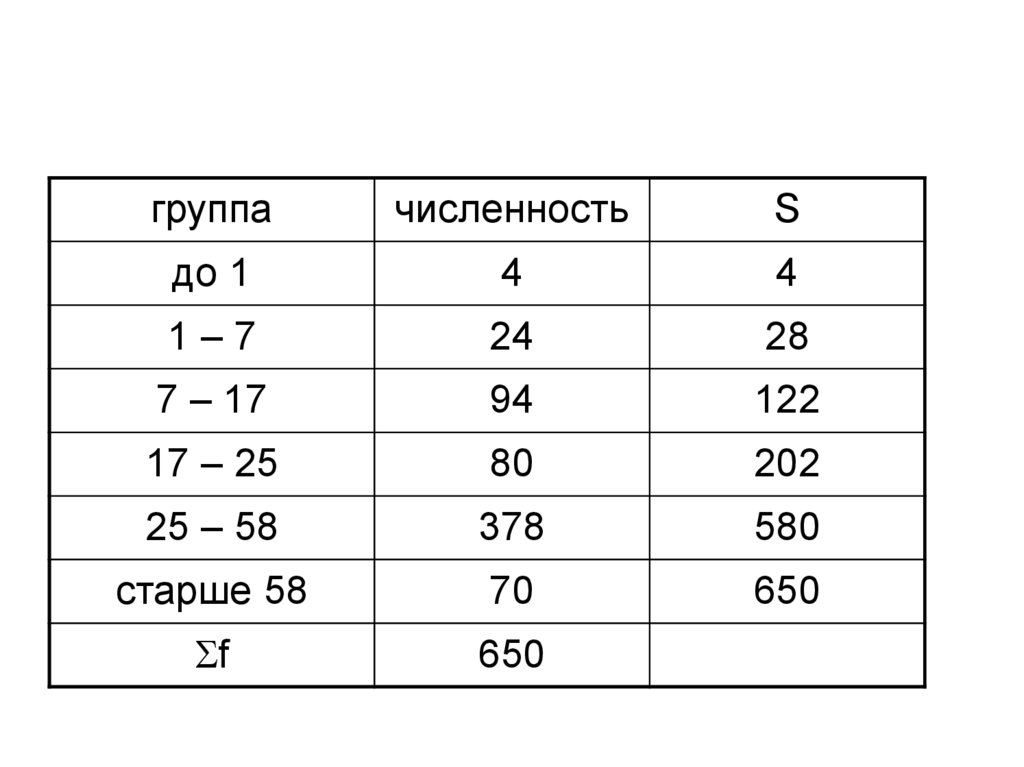
10.
группачисленность
S
до 1
4
4
1–7
24
28
7 – 17
94
122
17 – 25
80
202
25 – 58
378
580
старше 58
70
650
f
650
11.
x3
4
5
f
12
16
8
36
S
12
28
36
12.
промилле0/
00
продецимилле
0/
000
13.
ОВПЗплановое _ задание _ на _ предстоящий _ период
x100%
фактическое _ выполнение _ в _ базисном _ периоде
ОВВП
фактическое _ выполнение _ в _ отчетном _ периоде
х100%
плановое _ задание _ в _ отчетном _ периоде
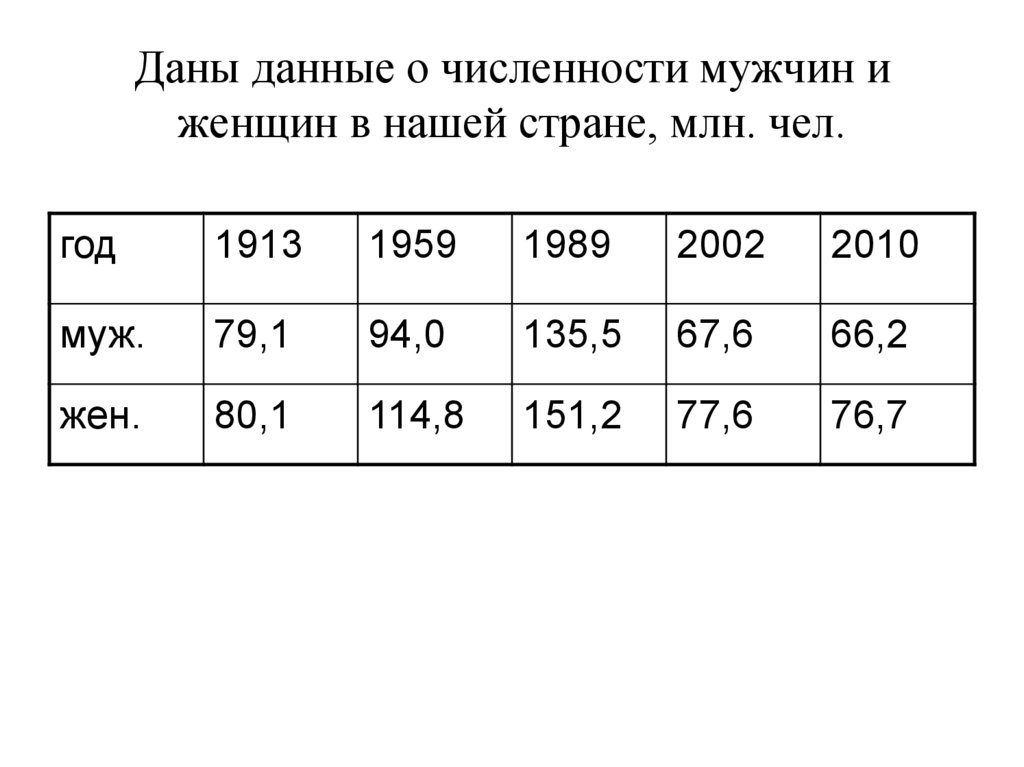
14. Даны данные о численности мужчин и женщин в нашей стране, млн. чел.
год1913
1959
1989
2002
2010
муж.
79,1
94,0
135,5
67,6
66,2
жен.
80,1
114,8
151,2
77,6
76,7
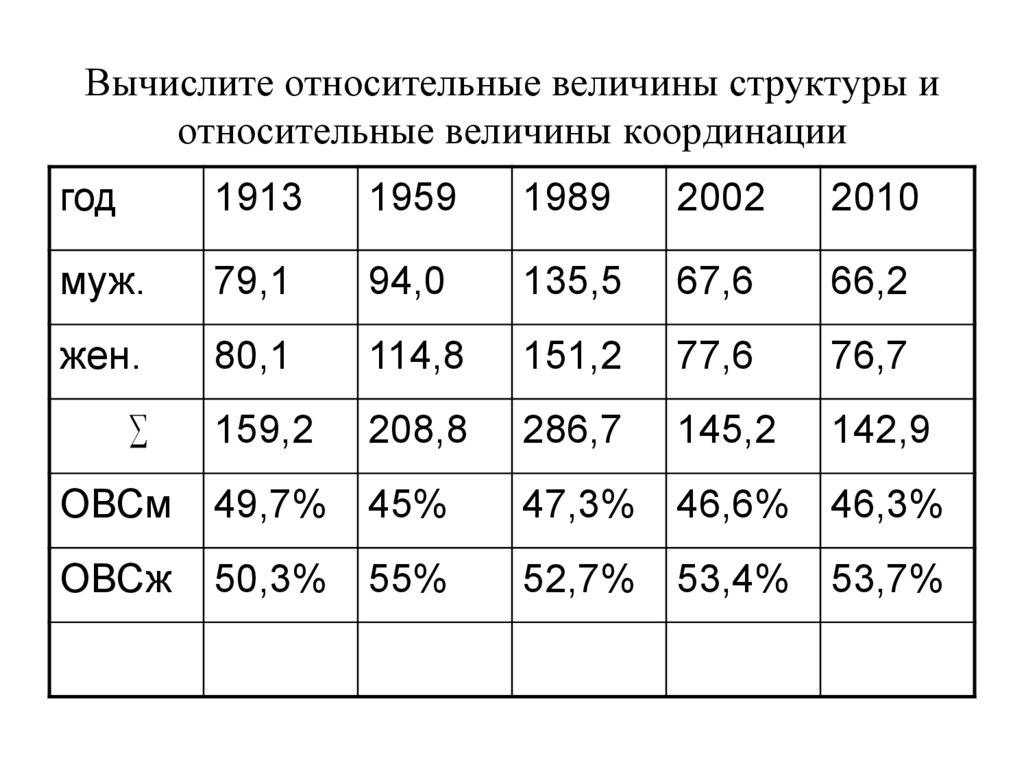
15. Вычислите относительные величины структуры и относительные величины координации
год1913
1959
1989
2002
2010
муж.
79,1
94,0
135,5
67,6
66,2
жен.
80,1
114,8
151,2
77,6
76,7
159,2
208,8
286,7
145,2
142,9
ОВСм
49,7%
45%
47,3%
46,6%
46,3%
ОВСж
50,3%
55%
52,7%
53,4%
53,7%
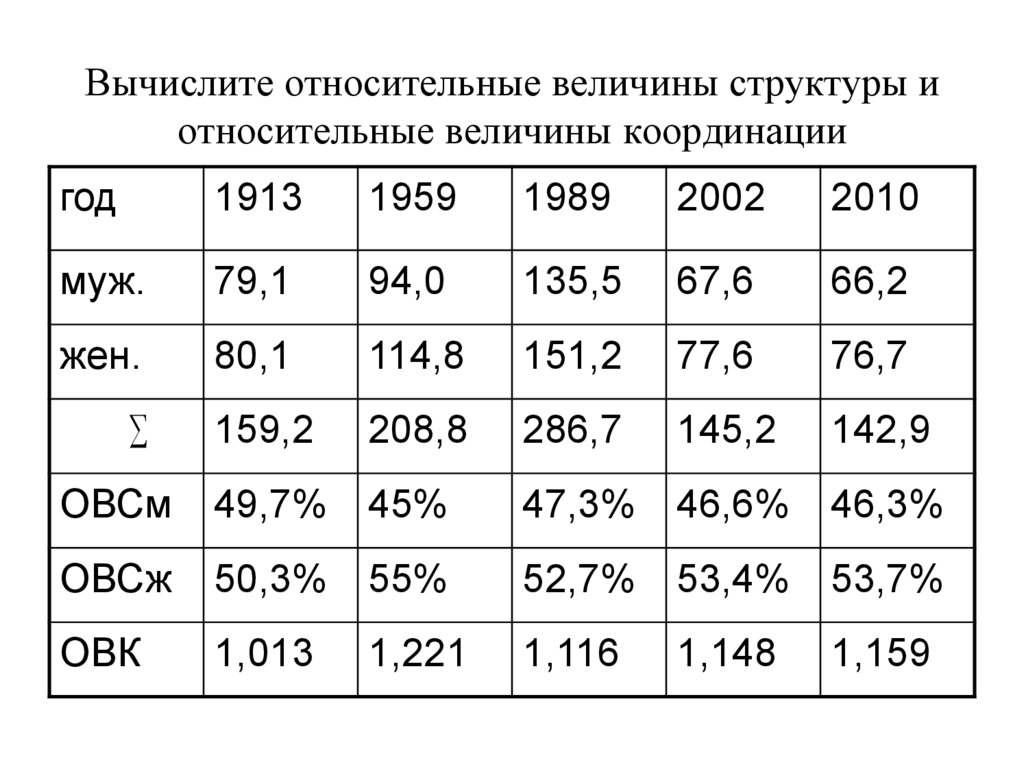
16. Вычислите относительные величины структуры и относительные величины координации
год1913
1959
1989
2002
2010
муж.
79,1
94,0
135,5
67,6
66,2
жен.
80,1
114,8
151,2
77,6
76,7
159,2
208,8
286,7
145,2
142,9
ОВСм
49,7%
45%
47,3%
46,6%
46,3%
ОВСж
50,3%
55%
52,7%
53,4%
53,7%
ОВК
1,013
1,221
1,116
1,148
1,159
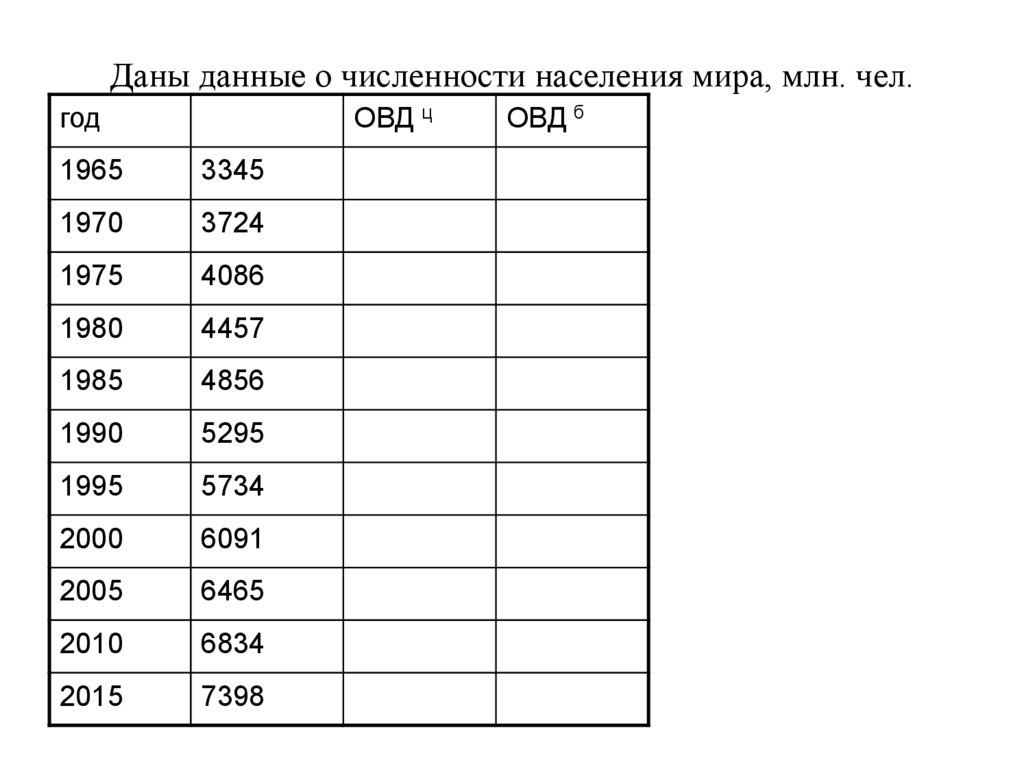
17. Даны данные о численности населения мира, млн. чел.
годОВД ц
1965
3345
1970
3724
1975
4086
1980
4457
1985
4856
1990
5295
1995
5734
2000
6091
2005
6465
2010
6834
2015
7398
ОВД б
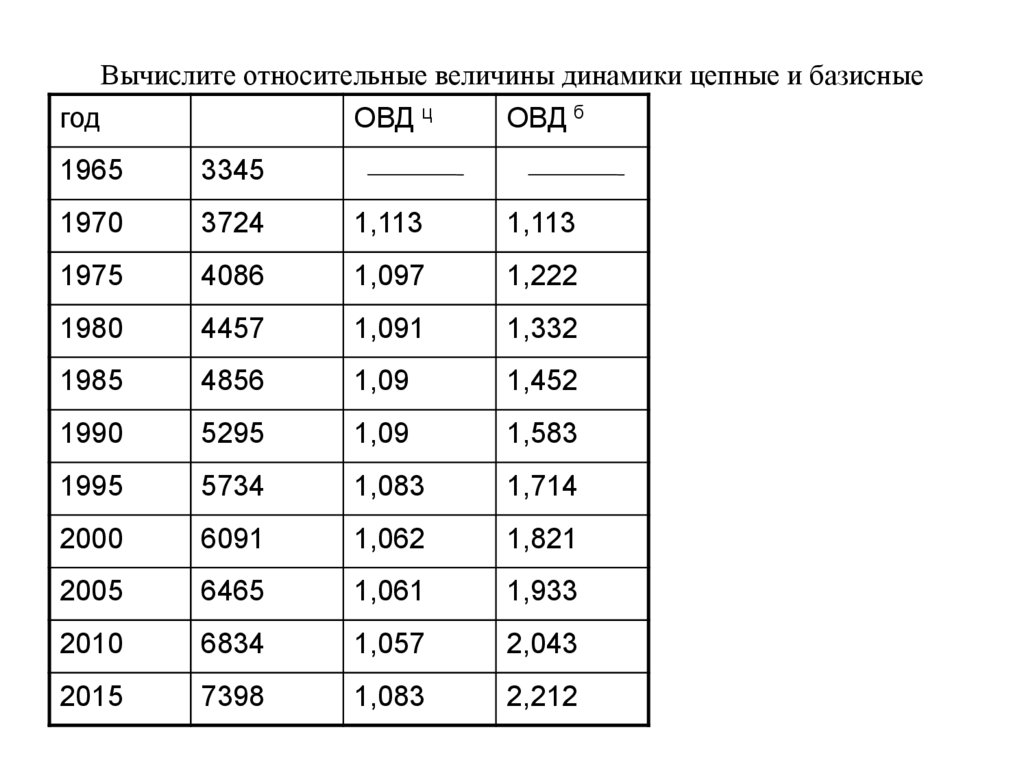
18. Вычислите относительные величины динамики цепные и базисные
годОВД ц
ОВД б
1965
3345
1970
3724
1,113
1,113
1975
4086
1,097
1,222
1980
4457
1,091
1,332
1985
4856
1,09
1,452
1990
5295
1,09
1,583
1995
5734
1,083
1,714
2000
6091
1,062
1,821
2005
6465
1,061
1,933
2010
6834
1,057
2,043
2015
7398
1,083
2,212
19. Средняя
Средняя величина - обобщающий
показатель, характеризующий типичный
уровень варианты в расчете на единицу
однородной совокупности в конкретных
условиях места и времени.
Средняя отражает то общее, что
скрывается в каждой единице
однородной совокупности.
20. Виды средних
• В экономике применяют следующиевиды средних величин:
• - средняя арифметическая;
• - средняя гармоническая;
• - степенная средняя;
• - средняя квадратическая;
• - средняя геометрическая;
• - средняя хронологическая.
21. Средняя арифметическая простая
xx
n
22.
Например, студент сдал сессию на оценки 3 3 4 4 5,необходимо рассчитать средний балл студента
3 3 4 4 5
x
3,8
5
23. Средняя арифметическая взвешенная
xx
f
f
24.
x3
4
5
f
12
16
8
3 12 4 16 5 8
x
3,889
12 16 8
25. .
x20 2 21 7 22 2 23 1 24 1 29 2
31 1 32 1 33 1 34 1 39 1
25,25 лет
20
26. .
x35 2 36 1 37 15 38 10 39 7 40 5
41 1 42 9 43 5 45 3
39,362 лет
58
27.
x fx
f
i
28. Даны данные по весу изделий
весизделий, кг
x
до 20
20-30
30-50
50-70
свыше 70
Число
изделий
f
5
15
30
18
2
29. Необходимо найти средний вес изделия
весизделий, кг
x
10-20
20-30
30-50
50-70
70-90
Число
изделий
f
5
15
30
18
2
xi
15
25
40
60
80
30. Решение:
15 5 25 15 40 30 60 18 80 2x
41,286кг
5 15 30 18 2
31. Средняя гармоническая
простаяx
n
1
x
взвешенная
x f
w
x
x f
w
x x
w x f
32. Степенная средняя
простаяx m
x
m
n
взвешенная
x f
f
m
x m
33. Средняя квадратическая
простаяx
x
2
n
взвешенная
x f
f
2
x
34. Средняя геометрическая
простаяx Пx
n
взвешенная
x
f
Пx
f
35. Средняя хронологическая
xnx1
x2 x3
2
2
x
n 1
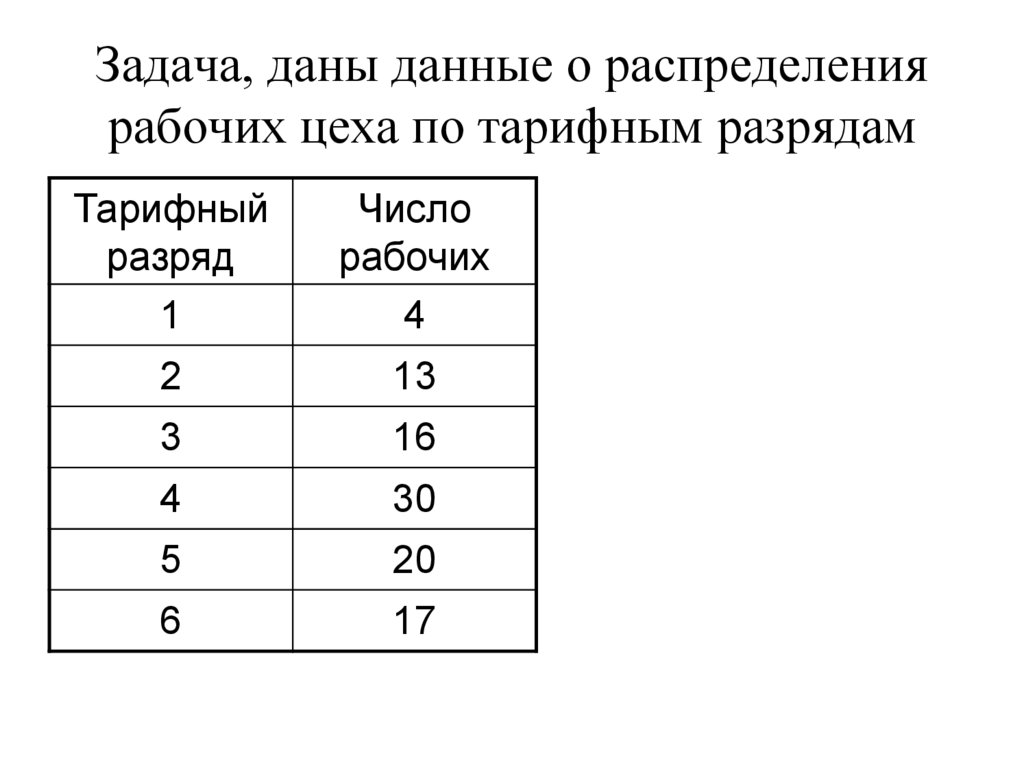
36. Задача, даны данные о распределения рабочих цеха по тарифным разрядам
Тарифныйразряд
1
Число
рабочих
4
2
13
3
16
4
30
5
20
6
17
37. Вычислите средний тарифный разряд рабочих в цехе
1 4 2 13 3 16 4 30 5 20 6 17x
4
4 13 16 30 20 17
38. Даны данные о распределении заводов в цементной промышленности по величине производственной мощности.
Произв.мощность, тыс. т
Число заводов
до 100
100-200
200-300
300-500
500-700
свыше 700
10
15
25
21
16
13
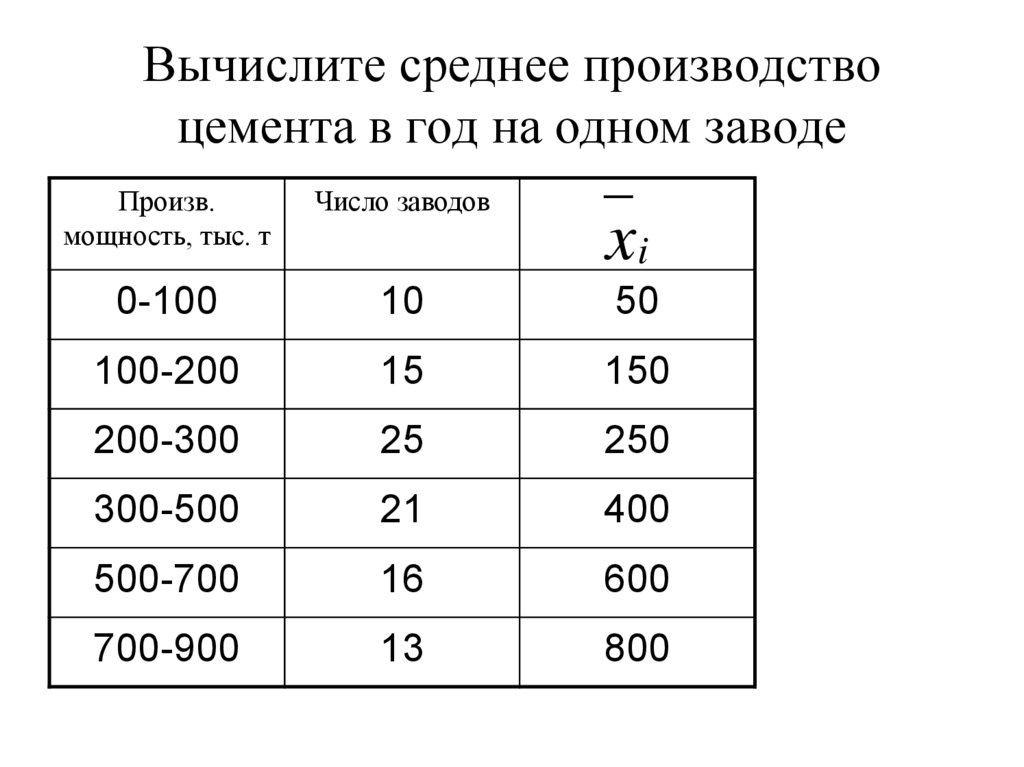
39. Вычислите среднее производство цемента в год на одном заводе
Произв.мощность, тыс. т
Число заводов
0-100
10
50
100-200
15
150
200-300
25
250
300-500
21
400
500-700
16
600
700-900
13
800
xi
40.
50 10 150 15 250 25 400 21 600 16 800 13x
374тыс.т
10 15 25 21 16 13
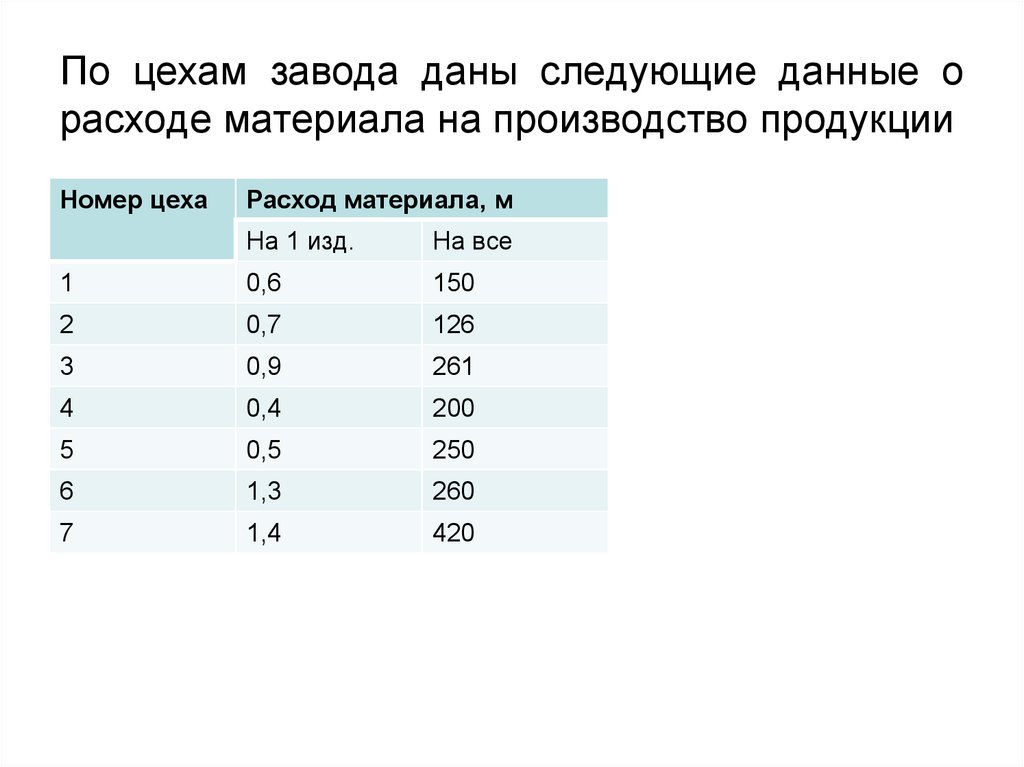
41. По цехам завода даны следующие данные о расходе материала на производство продукции
Номер цехаРасход материала, м
На 1 изд.
На все
1
0,6
150
2
0,7
126
3
0,9
261
4
0,4
200
5
0,5
250
6
1,3
260
7
1,4
420
42. Определите расход материала на одно изделие в среднем по заводу
xw
w
x
150 126 261 200 250 260 420
x
150 126 261 200 250 260 420
0,6 0,7 0,9 0,4 0,5 1,3 1,4
1667
x
0,751м
2220
43. Даны данные
группаIII квартал
IV квартал
Средняя
з/пл, руб.
Число
рабочих
Средняя
з/пл, руб.
1
8900
1000
9000
Фонд
з/пл,
тыс.руб.
9000
2
9200
2000
8700
10440
3
9500
800
8500
9350
44. Вычислите среднюю заработную плату в каждом квартале и на сколько процентов изменилась средняя заработная плата
x IIIx III
x f
f
8900 1000 9200 2000 9500 800
1000 2000 800
x III 9184,211 руб.
45.
x IVx IV
w
w
x
9000 10440 9350
9000 10440 9350
9000
8700
8500
x IV 8724,242 руб.
46.
x IVОВД
0,95
x III
0,95 100% 100% 5%
Средняя заработная плата в IV квартале по сравнению с III снизилась на 5%
47. Показатели центра распределения
x Мо Ме48. например
Даны данные о распределении рабочихцеха по тарифным разрядам
х
f
1
4
2
5
3
9
4
4
5
2
49. в интервальных рядах
f мо f мо 1Мо x мо h
( f мо f мо 1 ) ( f мо f мо 1 )
50. например: даны данные о распределении рабочих цеха по возрасту, лет
хдо 21
21-24
24-27
27-30
30-33
33-36
старше 36
f
1
3
7
9
5
3
2
30
51. Мо
9 7Мо 27 3
28 лет
(9 7) (9 5)
52. в дискретных рядах
х1
2
3
4
5
f
4
5
9
4
2
24
S
4
9
18
53. в интервальных рядах
fМе х м е h
2
S м е 1
f ме
54. .
хдо 21
21-24
24-27
27-30
30-33
33-36
старше 36
f
1
3
7
9
5
3
2
∑ 30
.S
1
4
11
20
55. Ме
3011
2
Ме 27 3
28,333 лет
9
56. размах вариации
R xmax xmin57. показатели вариации
х18-21
21-24
24-27
27-30
30-33
33-36
36-39
f
1
3
7
9
5
3
2
R 39 18 21год
58. линейное отклонение
d x xd пр
d взв
d
n
d f
f
59.
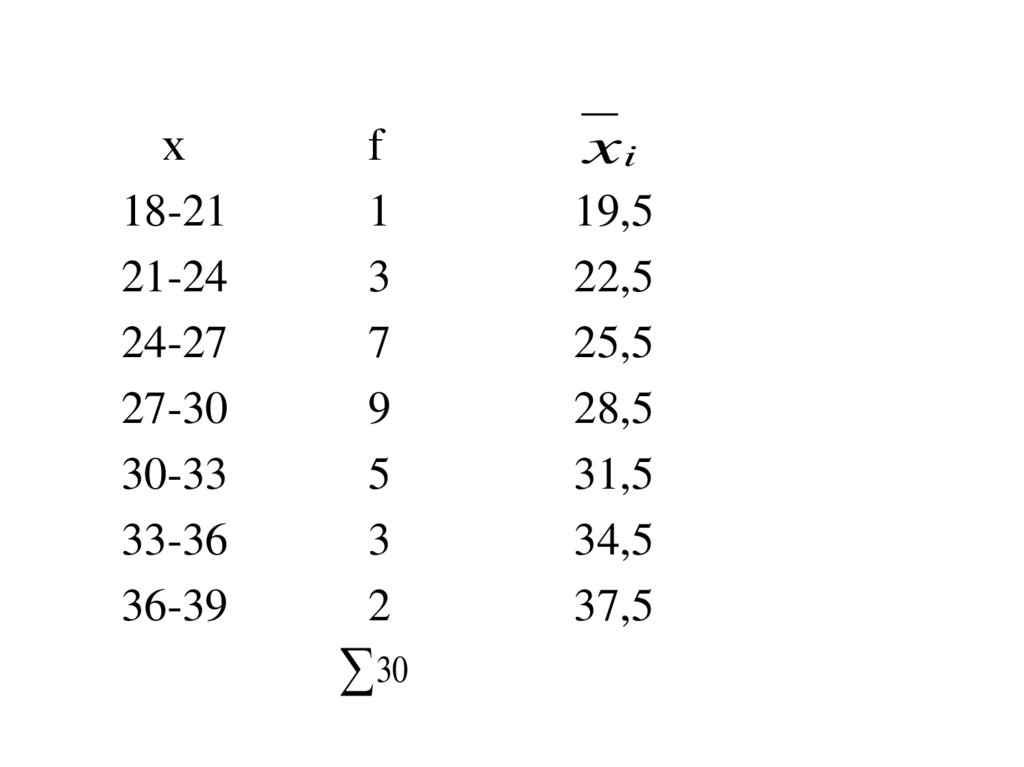
х18-21
21-24
24-27
27-30
30-33
33-36
36-39
f
1
3
7
9
5
3
2
30
xi
19,5
22,5
25,5
28,5
31,5
34,5
37,5
60. .
x fx
f
i
19,5 1 22,5 3 25,5 7 28,5 9 31,5 5 34,5 3 37,5 2
х
30
х 28,6 лет
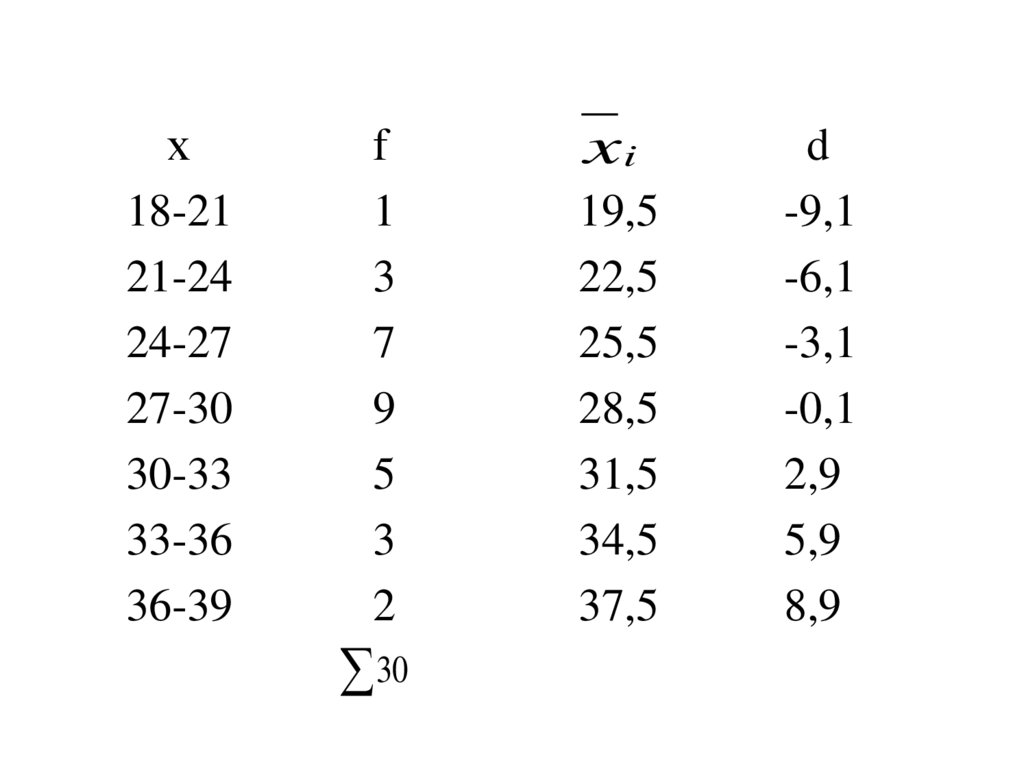
61.
х18-21
21-24
24-27
27-30
30-33
33-36
36-39
f
1
3
7
9
5
3
2
30
xi
19,5
22,5
25,5
28,5
31,5
34,5
37,5
d
-9,1
-6,1
-3,1
-0,1
2,9
5,9
8,9
62. .
d fd
f
.
9,1 1 6,1 3 3,1 7 0,1 9 2,9 5 5,9 3 8,9 2
d
30
d 3,333 лет
63. дисперсия
2пр
2
x x)
взв
d
2
n
x x)
f
2
n
2
f
d f
f
2
64. среднее квадратическое отклонение
( x x)пр
в зв
2
2
n
d
( х х) f
f
2
2
n
d f
f
2
65. коэффициент вариации
x100%
Совокупность однородная если
˂ 33%
66. .
22
d
f
f
2
2
2
2
2
2
2
9
,
1
1
6
,
1
3
3
,
1
7
0
,
1
9
2
,
9
5
5
,
9
3
8
,
9
2
2
30
2 18,89
67. .
18,89 4,346 лет2
4,346
100%
100 15,2%
28,6
х
совокупность однородная
68. Задача1: по результатам исследования получены следующие данные о ценах на яблоки, руб.
2932
29
35
Вычислите показатели вариации
34
33
69. Решение:
R 35 29 6 руб.х 29 32 29 35 34 33
х
32 руб.
n
6
d
d
n
2
2
d
n
3 0 3 3 2 1
2 руб.
6
32 0 2 32 32 2 2 12
5,333
6
2 5,333 2,309 руб.
2,309
100%
100 7,2%
32
х
совокупность однородная
70. Задача 2: дано распределение учителей средних школ района по стажу работы
стажчисло
работы,
учителей
лет
8
14
9
20
10
30
11
24
12
12
Вычислите показатели вариации и показатели
центра распределения
71. Решение:
R 12 8 4годах f 8 14 9 20 10 30 11 24 12 12
х
10 лет
100
f
d f 2 14 1 20 0 30 1 24 2 12
d
0,96года
100
f
d f 2 14 1 20 0 30 1 24 2 12
1,48
100
f
2
2
2
2
2
2
2
2 1,48 1,217 лет
1,217
100%
100 12,2%
10
х
Мо 10 лет
Ме 10 лет
совокупность однородная
72. Задача 3: дано распределение магазинов города по товарообороту
Группы магазинов повеличине ТО, тыс. руб.
Число
магазинов
40-50
2
50-60
4
60-70
7
70-80
10
80-90
15
90-100
20
100-110
22
110-120
11
120-130
6
130-140
3
100
Вычислите показатели вариации и показатели центра распределения
73. Решение:
R 140 40 100тыс. руб.x f
x
f
i
45 2 55 4 65 7 75 10
94,2тыс. руб.
100
d x x
d f 49,2 2 39,2 4 29,2 7 19,2 10
d
15,792тыс. руб.
100
f
d f 49,2 2 39,2 4 29,2 7 19,2 10
399,36
100
f
2
2
2
2
2
2
2 399,36 19,984тыс. руб.
19,984
100%
100 21,2%
94,2
х
совокупность однородная
74. Мода и Медиана
22 20Мо 100 10
101,538тыс. руб.
(22 20) (22 11)
50 38
Ме 90 10
96тыс. руб.
20
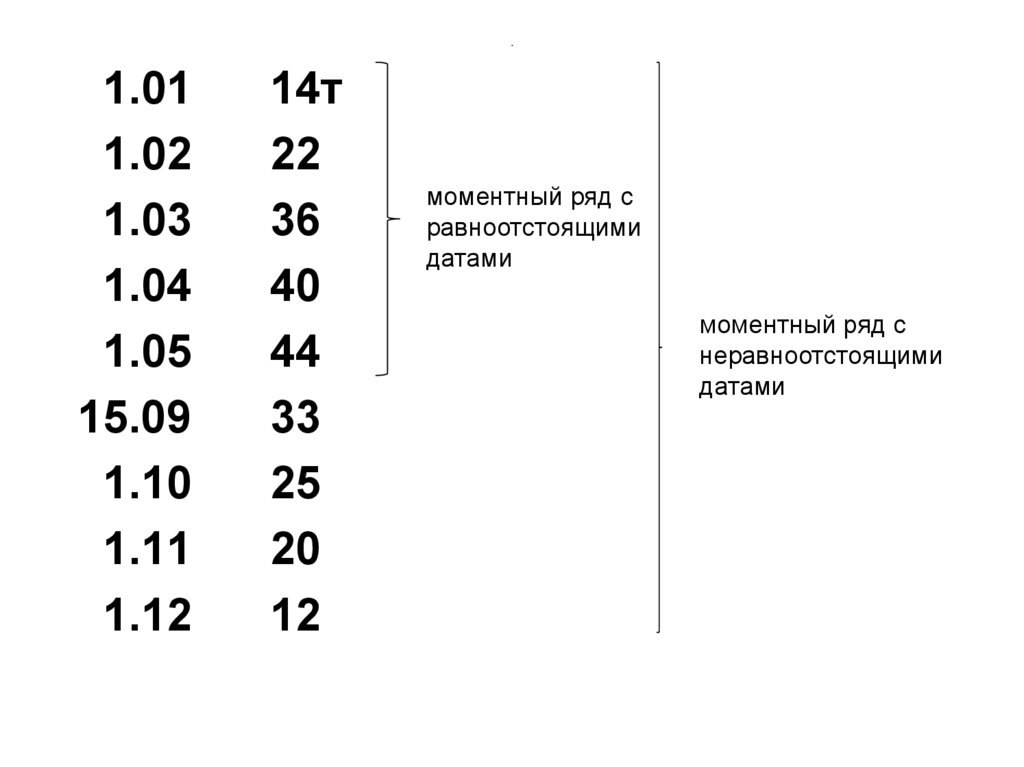
75. .
1.011.02
1.03
1.04
1.05
15.09
1.10
1.11
1.12
14т
22
36
40
44
33
25
20
12
моментный ряд с
равноотстоящими
датами
моментный ряд с
неравноотстоящими
датами
76. .
19861987
1988
1989
1990
1991
1992
1993
1997
10тыс.пар
12
15
15
интервальный
ряд с равными
18
интервалами
20
22
19
16
интервальный
ряд с неравными
интервалами
77. В интервальных рядах с равными интервалами
yy
n
78. с 86 по 93 г.г.
10 12 15 15 18 20 22 19y
16,375тыс.пар
8
79. В моментных рядах с равноотстоящими датами
yny1
y2 y3
2
2
y
n 1
80. с 1.01 по 1.05
1444
22 36 40
2
2
y
31,75т.
5 1
81. В интервальных рядах с неравными интервалами и в моментных рядах с неравноотстоящими датами
yy t
t
82. с 86 по 97 г.г.
10 1 12 1 15 2 18 1 20 1 22 1 19 4 16 1y
1 1 2 1 1 1 4 1
y 17тыс.пар
83. с 1.01 по 1.12
y14 1 22 1 36 1 40 1 44
84. .
14 1 22 1 36 1 40 1 44 4,5 33 0,5y
1 1 1 1 4,5 0,5
25 1 20 1 12 1
31,958т.
1 1 1
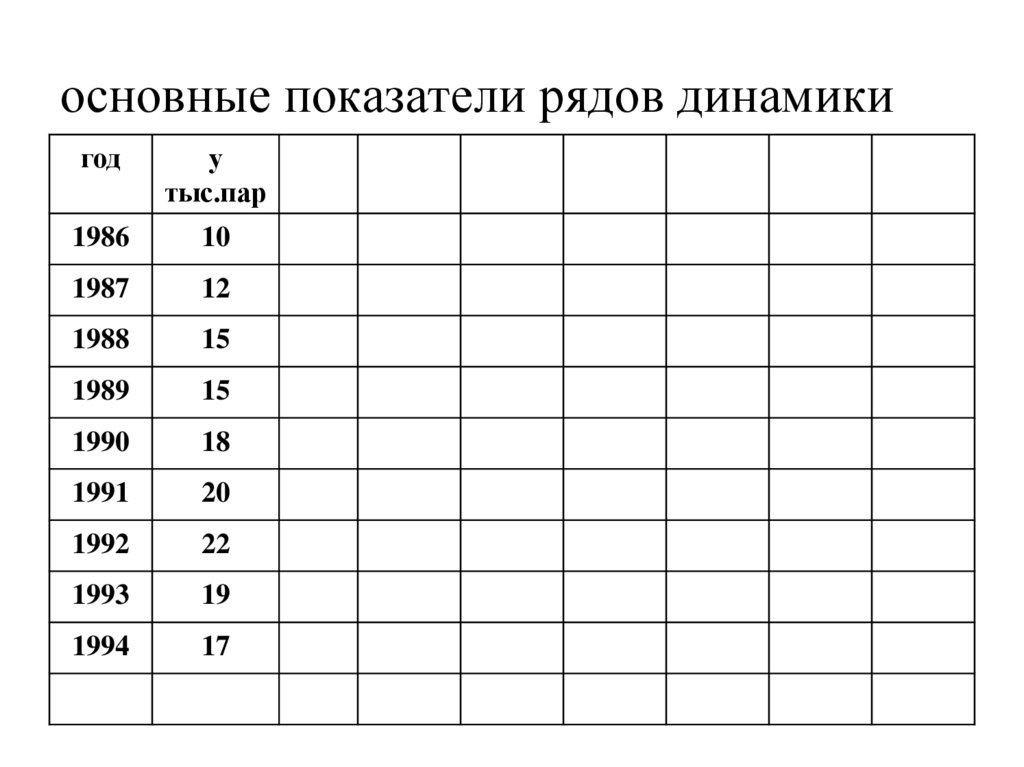
85. основные показатели рядов динамики
году
тыс.пар
1986
10
1987
12
1988
15
1989
15
1990
18
1991
20
1992
22
1993
19
1994
17
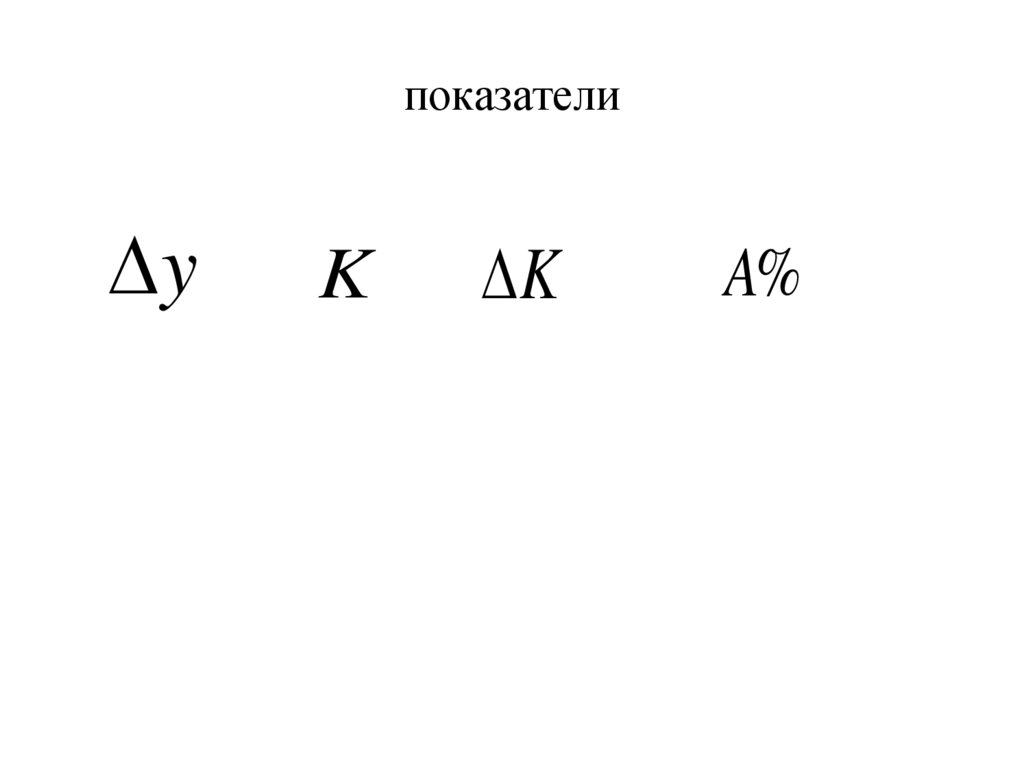
86. показатели
yK
K
A%
87. Абсолютный прирост
y yi yбy уi yi 1
ц
y y i y o
б
y
ц
y
б
n
88. .
y бгод
y
y
1986
10
-
-
1987
12
2
2
1988
15
3
5
1989
15
0
5
1990
18
3
8
1991
20
2
10
1992
22
2
12
1993
19
-3
9
1994
17
-2
7
ц
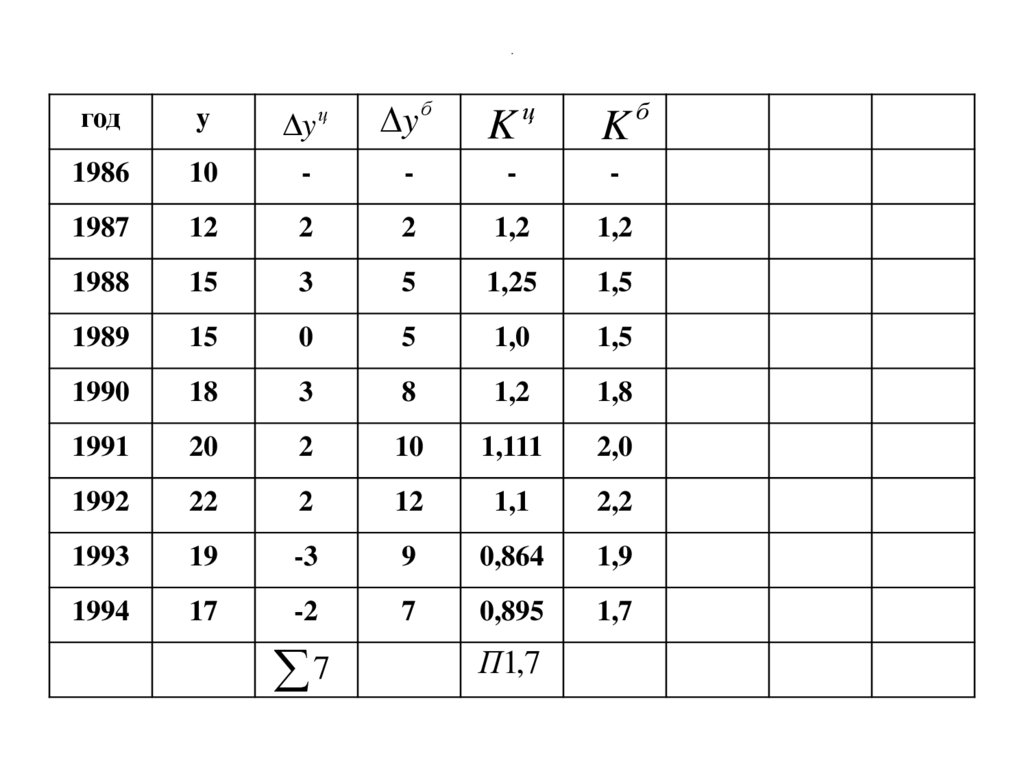
7
89. Темп роста
yiK
yб
yi
K
yi 1
yi
K
yo
ц
ПK K
ц
б
б
n
90. .
y бKц
-
-
-
-
12
2
2
1,2
1,2
1988
15
3
5
1,25
1,5
1989
15
0
5
1,0
1,5
1990
18
3
8
1,2
1,8
1991
20
2
10
1,111
2,0
1992
22
2
12
1,1
2,2
1993
19
-3
9
0,864
1,9
1994
17
-2
7
0,895
1,7
год
y
y
1986
10
1987
ц
7
П1,7
Kб
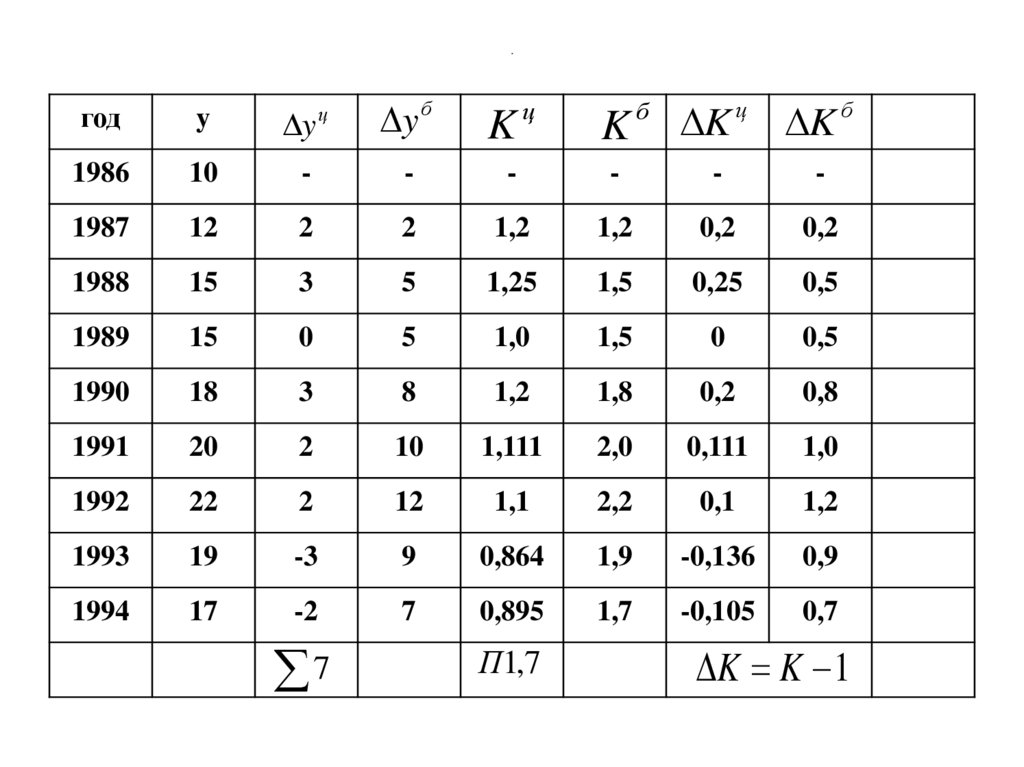
91. Темп прироста
y iK
yб
ц
y i
K
yi 1
ц
yi
K
yo
б
б
92. .
y бц
б
K
ц
K
год
y
y
1986
10
-
-
-
-
-
-
1987
12
2
2
1,2
1,2
0,2
0,2
1988
15
3
5
1,25
1,5
0,25
0,5
1989
15
0
5
1,0
1,5
0
0,5
1990
18
3
8
1,2
1,8
0,2
0,8
1991
20
2
10
1,111
2,0
0,111
1,0
1992
22
2
12
1,1
2,2
0,1
1,2
1993
19
-3
9
0,864
1,9
-0,136
0,9
1994
17
-2
7
0,895
1,7
-0,105
0,7
ц
7
K
П1,7
K
б
K K 1
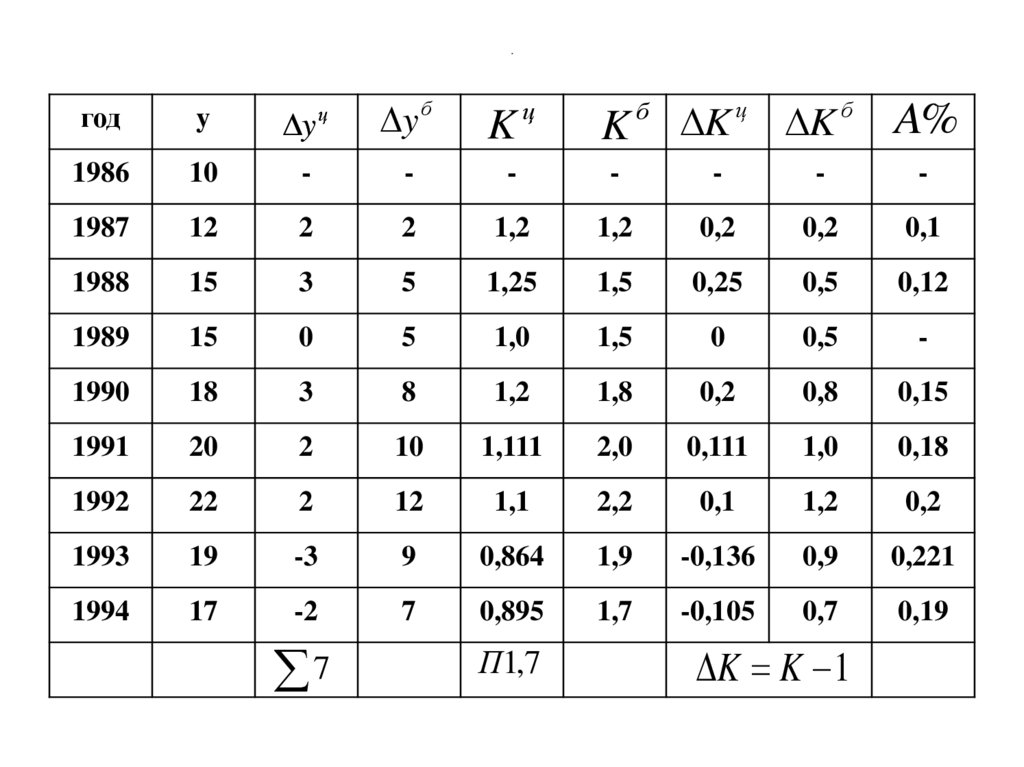
93. Абсолютное значение одного процента прироста
цyi
A%
100%
ц
K i
94. .
y бц
б
K
ц
K
б
год
y
y
1986
10
-
-
-
-
-
-
-
1987
12
2
2
1,2
1,2
0,2
0,2
0,1
1988
15
3
5
1,25
1,5
0,25
0,5
0,12
1989
15
0
5
1,0
1,5
0
0,5
-
1990
18
3
8
1,2
1,8
0,2
0,8
0,15
1991
20
2
10
1,111
2,0
0,111
1,0
0,18
1992
22
2
12
1,1
2,2
0,1
1,2
0,2
1993
19
-3
9
0,864
1,9
-0,136
0,9
0,221
1994
17
-2
7
0,895
1,7
-0,105
0,7
0,19
ц
7
K
П1,7
K
K K 1
A%
95. Средние показатели рядов динамики
Средний уровеньy
y
n
10 12 15 15 18 20 22 19 17
y
9
y 16,444тыс.пар
96. Средний абсолютный прирост
yy
m
ц
y n yn yo
m
m
б
m n 1
2 3 0 3 2 2 3 2
y
8
7 17 10
0,875тыс.пар
8
8
97. Средний темп роста
Km
ПK
ц
m
K
б
n
m
yn
yo
K 8 1,2 1,25 1 1,2 1,111 1,1 0,864 0,895
17
8
1,7 8
1,069
10
98. Средний темп прироста
K K 100% 100%K 1,069 100 100 6,9%
99. /
20002001
2002
2003
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
18,5
32,9
30,1
17,5
19,1
43,5
45,4
26
26,9
52,4
58,9
32,1
32,4
59,5
62,2
32,3
100. /
2000(18,5+32,9+30,1+17,5)/4= 24,75
2001
(19,1+43,5+45,4+26)/4=
2002
(26,9+52,4+58,9+32,1)/4= 42,575
2003
(32,4+59,5+62,2+32,3)/4= 46,6
33,5
101. /
20002001
2002
2003
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
1 квартал
2 квартал
3 квартал
4 квартал
18,5
32,9
30,1
17,5
19,1
43,5
45,4
26
26,9
52,4
58,9
32,1
32,4
59,5
62,2
32,3
27,167
26,833
22,233
26,7
36
38,3
32,767
35,1
46,067
47,8
41,133
41,333
51,367
51,333
102. Выравнивание по прямой
Уравнение прямой или уравнение трендаyt a0 a1 t
где:
yt уровень ряда (расчетный)
a0 и a1 параметры уравнения
t время, т.е. порядковый номер интервала или
момента времени
103. Метод наименьших квадратов
a0 n a1 t ya0 t a1 t y t
2
104. .
t 0a0 n y
a1 t y t
2
a0
a1
y
n
y t
t
2
105. .
Среднее квадратическое отклонениеt
(y y )
2
t
n
Коэффициент вариации
t
y
100%
106. .
году
тыс.пар
t
1986
10
-4
1987
12
-3
1988
15
-2
1989
15
-1
1990
18
0
1991
20
1
1992
22
2
1993
19
3
1994
17
4
148
0
107. .
году
тыс.пар
1986
10
-4
16
1987
12
-3
9
1988
15
-2
4
1989
15
-1
1
1990
18
0
0
1991
20
1
1
1992
22
2
4
1993
19
3
9
1994
17
4
16
148
t t
2
0 60
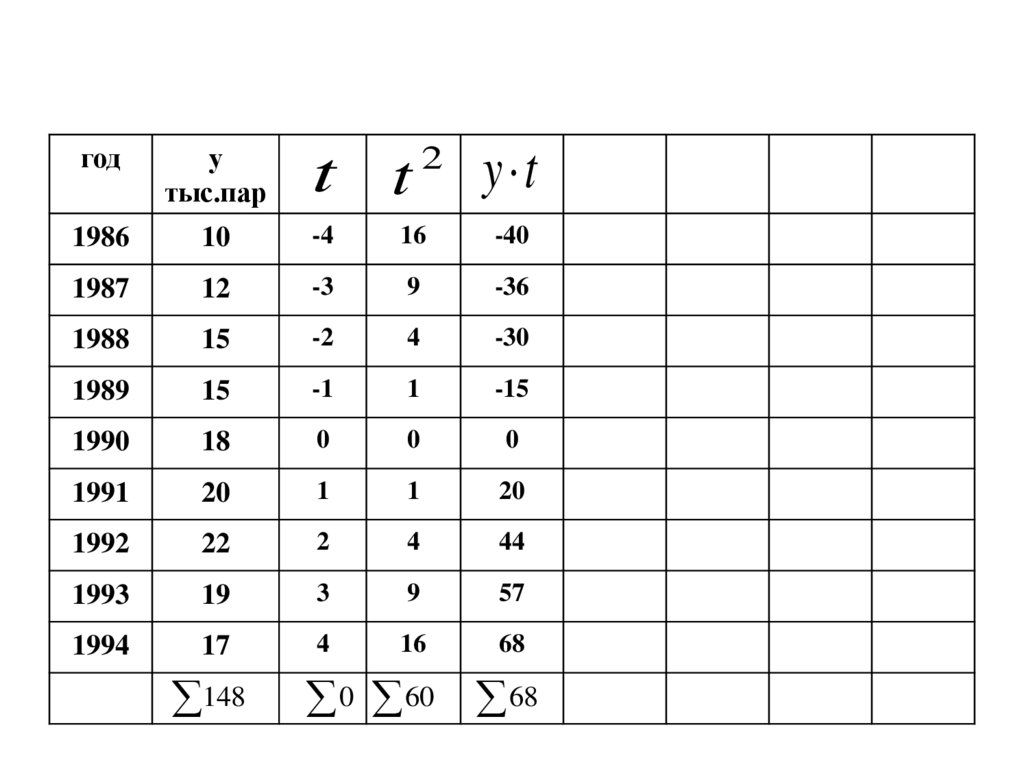
108. .
y tгод
у
тыс.пар
1986
10
-4
16
-40
1987
12
-3
9
-36
1988
15
-2
4
-30
1989
15
-1
1
-15
1990
18
0
0
0
1991
20
1
1
20
1992
22
2
4
44
1993
19
3
9
57
1994
17
4
16
68
148
t t
2
0 60 68
109. .
a0a1
y 148
16,444
n
9
y t 68
1,133
t 60
2
yt 16,444 1,133 t
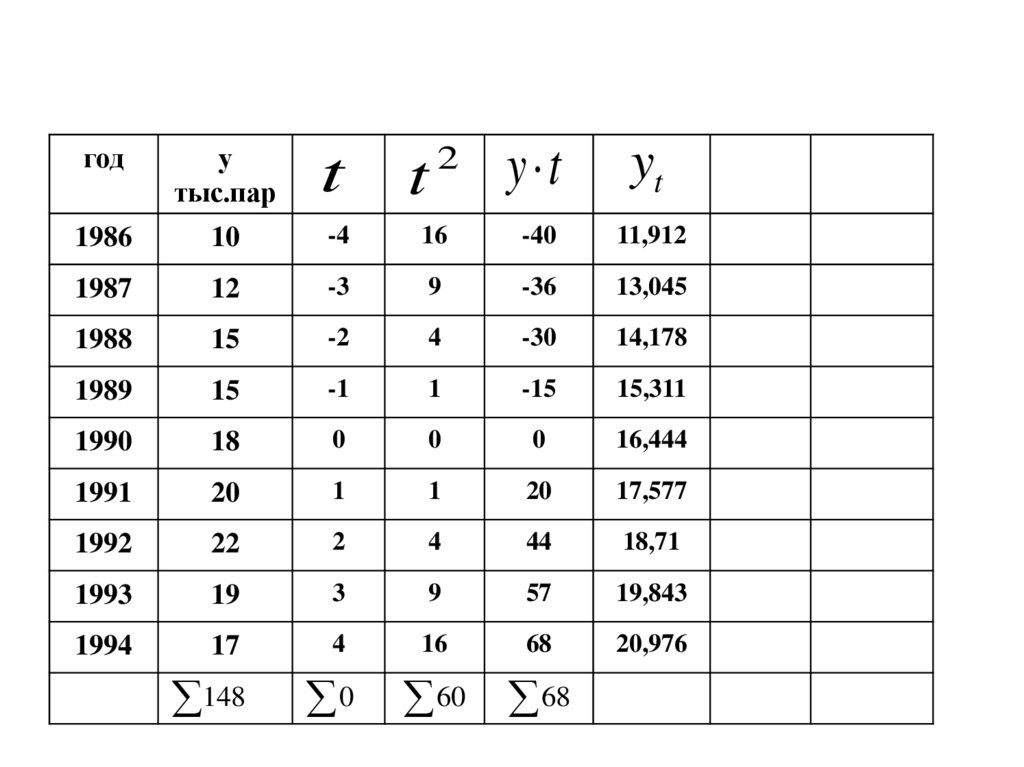
110. .
y tyt
16
-40
11,912
-3
9
-36
13,045
15
-2
4
-30
14,178
1989
15
-1
1
-15
15,311
1990
18
0
0
0
16,444
1991
20
1
1
20
17,577
1992
22
2
4
44
18,71
1993
19
3
9
57
19,843
1994
17
4
16
68
20,976
год
у
тыс.пар
t
1986
10
-4
1987
12
1988
148
0
t
2
60 68
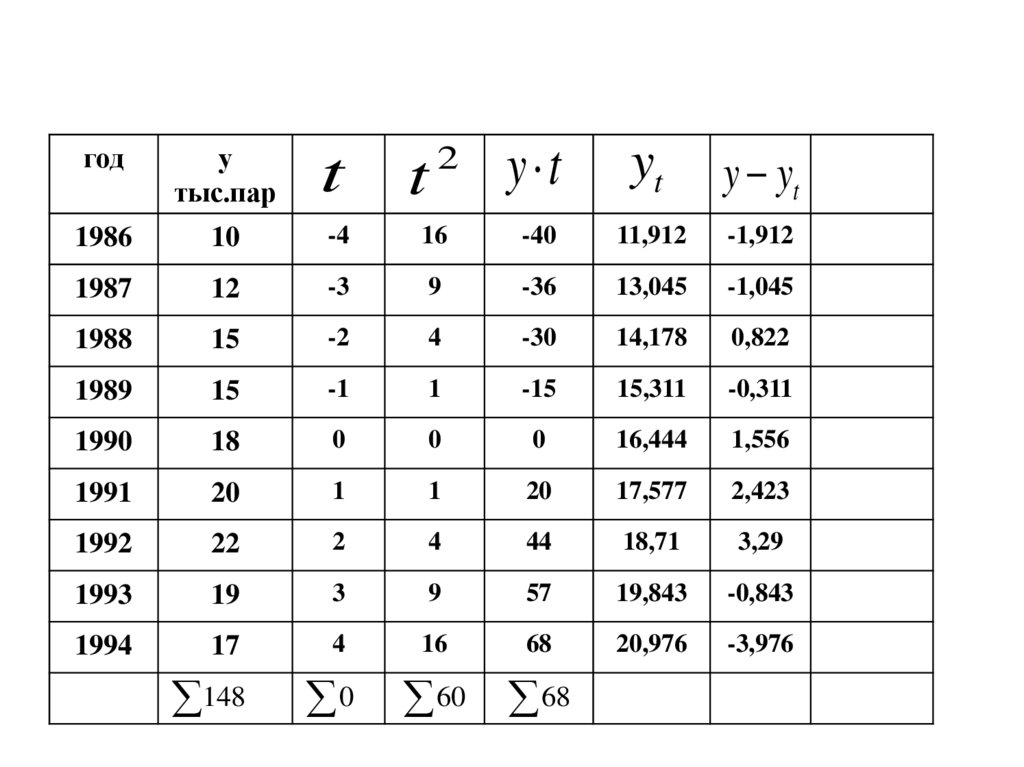
111. .
y tyt
y yt
16
-40
11,912
-1,912
-3
9
-36
13,045
-1,045
15
-2
4
-30
14,178
0,822
1989
15
-1
1
-15
15,311
-0,311
1990
18
0
0
0
16,444
1,556
1991
20
1
1
20
17,577
2,423
1992
22
2
4
44
18,71
3,29
1993
19
3
9
57
19,843
-0,843
1994
17
4
16
68
20,976
-3,976
год
у
тыс.пар
t
1986
10
-4
1987
12
1988
148
0
t
2
60 68
112. .
y tyt
16
-40
11,912
-1,912
3,656
-3
9
-36
13,045
-1,045
1,092
15
-2
4
-30
14,178
0,822
0,676
1989
15
-1
1
-15
15,311
-0,311
0,097
1990
18
0
0
0
16,444
1,556
2,421
1991
20
1
1
20
17,577
2,423
5,871
1992
22
2
4
44
18,71
3,29
10,824
1993
19
3
9
57
19,843
-0,843
0,711
1994
17
4
16
68
20,976
-3,976
15,809
год
у
тыс.пар
t
1986
10
-4
1987
12
1988
148
0
t
2
60 68
y yt ( y yt )
2
41,157
113. ю
t2
(
y
y
)
t
n
41,157
4,573 2,138
9
t
2,138
100%
100 13%
16,444
y
Колеблемость около тренда допустимая
114. ю
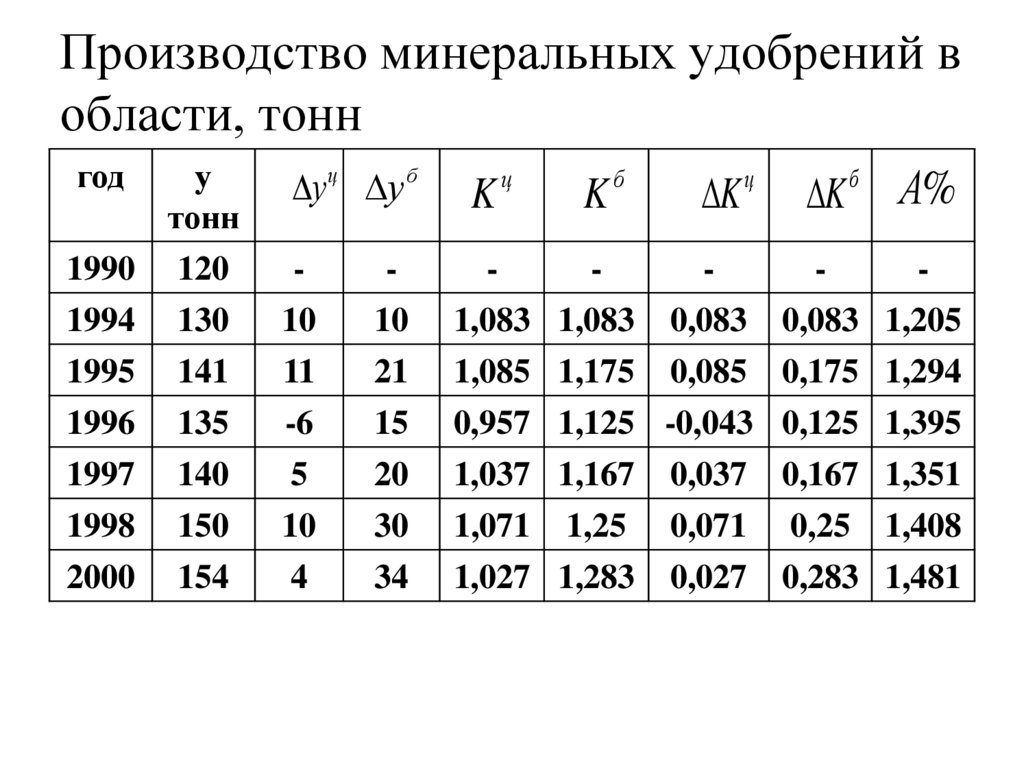
115. Производство минеральных удобрений в области, тонн
год1990
1994
1995
1996
1997
1998
2000
у
тонн
120
130
141
135
140
150
154
116. Производство минеральных удобрений в области, тонн
году
б
ц
б
у ц у б K ц
А
%
K
K
K
тонн
1990
1994
1995
120
130
141
10
11
10
21
1,083 1,083
1,085 1,175
0,083
0,085
1996
1997
1998
135
140
150
-6
5
10
15
20
30
0,957 1,125 -0,043 0,125 1,395
1,037 1,167 0,037 0,167 1,351
1,071 1,25 0,071 0,25 1,408
2000
154
4
34
1,027 1,283
0,027
0,083 1,205
0,175 1,294
0,283 1,481
117. средние
y t 120 4 130 141 135 140 150 2 154y
11
t
y 134,545тонн
34
у
3,4тонны
10
К 10 1,283 1,025
К 2,5%
Вывод:
За период с 1990 по 2000 г.г.
в среднем ежегодно в области
производилось 134,545 тонн
минеральных удобрений
За рассматриваемый период
времени в среднем ежегодно
производство минеральных
удобрений увеличивалось
на 3,4 тонны, или в 1,025 раза,
или на 2,5%
118. Индексы
Индексами называют относительныевеличины трех видов:
- динамики
- степени выполнения плана и
- сравнения
Индексы делят на два вида:
- индивидуальные и
- общие
119. Экономические показатели в статистике
p - цена единицы продукцииz - себестоимость единицы продукции
q - физический объем или количество
продукции
pq = ТО - товарооборот
zq = З - затраты на производство
120.
121. Индивидуальные индексы
p1ip
p0
индивидуальный индекс цены
z1
iz
z0
индивидуальный индекс себестоимости
q1
iq
q0
индивидуальный индекс объема
Например:
p на хлеб пш. I сорта в 2015 г. = 18 руб.
p на хлеб пш. I сорта в 2016 г. = 19 руб.
p1 19
ip
1,056
p0 18
цена на хлеб пш. I сорта
в 2016 году по сравнению с 2015
изменилась в 1,056 раза или
увеличилась на 5,6%
122. Агрегатные индексы
Общий индекс ценыIp
p q
p q
1
1
0
1
Абсолютное изменение товарооборота за счет
изменения цены
ТОp p1q1 p0 q1
123. Агрегатные индексы
Общий индекс объемаIq
q p
q p
1
0
0
0
Абсолютное изменение товарооборота за счет
изменения объема
ТОq q1 p0 q0 p0
ТО ТО p ТОq
Общее изменение
товарооборота
124. Агрегатные индексы
Общий индекс себестоимостиIz
z q
z q
1
1
0
1
Абсолютное изменение затрат за счет изменения
себестоимости
Зz z1q1 z0 q1
125. Агрегатные индексы
Общий индекс объемаIq
q z
q z
1
0
0
0
Абсолютное изменение затрат за счет изменения
объема
Зq q1 z0 q0 z0
З Зz Зq
Общее изменение
затрат
126. Общие индексы товарооборота и затрат
Общий индекс товарооборотаIТО
ТО p q
ТО p q
1
1
1
0
0
0
Общее изменение товарооборота
ТО ТО1 ТО0
p1q1 p0 q0
ТО p ТОq
127. Общие индексы товарооборота и затрат
Общий индекс затратIЗ
З
z q
З z q
1
1
1
0
0
0
Общее изменение затрат
З З1 З0
z1q1 z0 q0
З z З q
128. Взаимосвязь индексов или индексные системы
I p I q I ТОI z Iq IЗ
129. Индексы переменного состава, постоянного состава и структурных сдвигов
IpIp
пер.
пост.
p1 p1 q1 p0 q0
p0
q1
q0
p q p q
q
q
1
1
0
1
Ip
стр.сдв.
1
p q p q
q
q
0
1
1
I
пер.
1
I
пост.
I
стр.сдв.
0
0
0
130. Средние индексы
Ipp q
p q
1
1
0
1
131. .
Ipp
p
1
q1
0
q1
1
ip
p1
p
p0 1
p0
ip
Iq
q p
q p
iq
0
0
0
z
z
iz
iq
1
q1
q1 iq q0
q0
Iz
Iq
p
p
i
1
q1
0
q1
z1
z
z0 1
z0
iz
q z
q z
1
0
0
0
1
q1
q1
p
ТО
ТО
i
1
1
p
i q p
q p
q
0
0
z
z
i
1
1
0
0
q1
q1
z
i ТО
ТО
q
0
0
З
З
i
1
1
z
i q z
q z
q1
q1 iq q0
q0
x
q
0
0
0
0
i З
З
q
0
0
w
w
x
x f
x
f
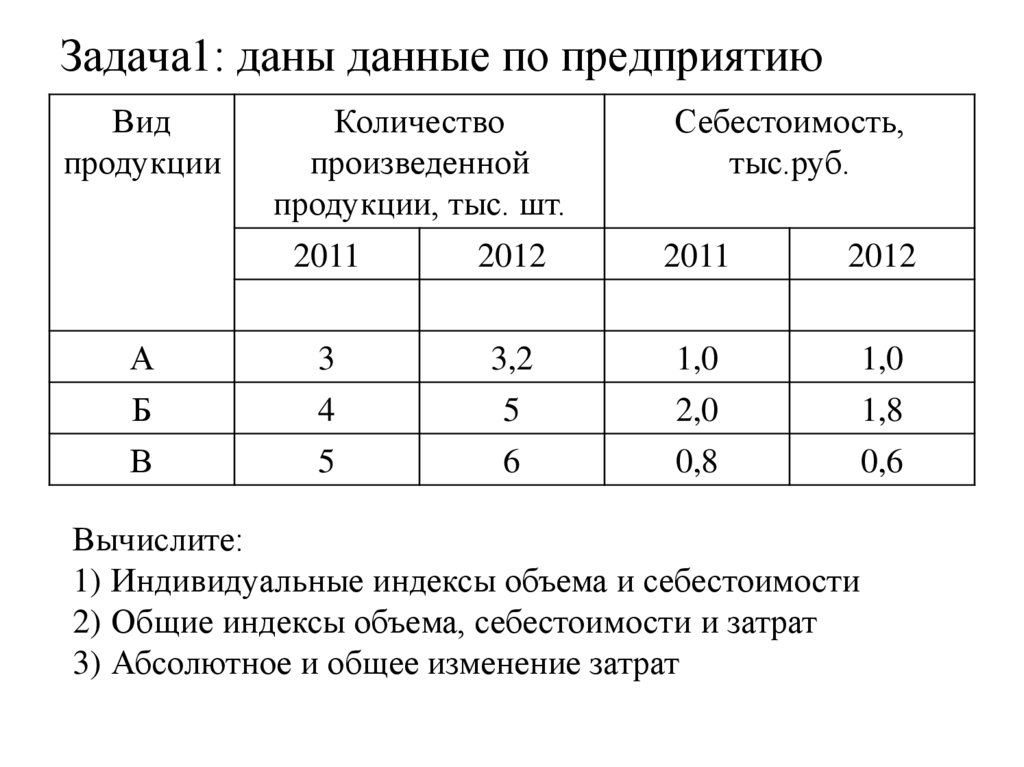
132. Задача1: даны данные по предприятию
Видпродукции
Количество
произведенной
продукции, тыс. шт.
2011
2012
Себестоимость,
тыс.руб.
2011
2012
А
Б
3
4
3,2
5
1,0
2,0
1,0
1,8
В
5
6
0,8
0,6
Вычислите:
1) Индивидуальные индексы объема и себестоимости
2) Общие индексы объема, себестоимости и затрат
3) Абсолютное и общее изменение затрат
133.
134. .
Iqq
q
1
z0
Iz
z
z
1
q1
0
q1
3,2 1 5 2 6 0,8
3 1 4 2 5 0,8
0 z0
1 3,2 1,8 5 0,6 6
135. .
IqIz
IЗ
q z
3,2 1 5 2 6 0,8 18
1,2
3 1 4 2 5 0,8
15
q z
z q
1 3,2 1,8 5 0,6 6 15,8
0,878
18
18
z q
z q 15,8
I З I z I q 1,054
1,053
z q 15
1
0
0
0
1
1
0
1
1
1
0
0
Зq q1 z0 q0 z0 18 15 3млн. руб.
Зz z1q1 z0 q1 15,8 18 2,2 млн. руб.
З z1q1 z0 q0 15,8 15 0,8 млн. руб.
З Зz Зq 2,2 3 0,8 млн. руб.
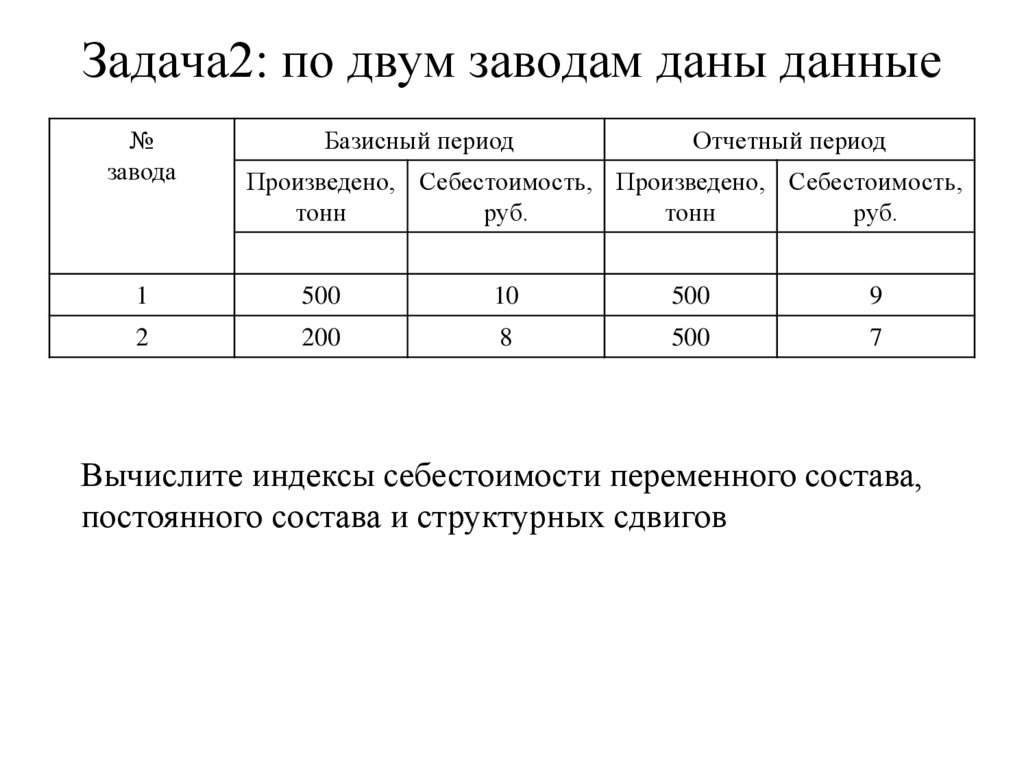
136. Задача2: по двум заводам даны данные
№завода
Базисный период
Отчетный период
Произведено, Себестоимость, Произведено, Себестоимость,
тонн
руб.
тонн
руб.
1
500
10
500
9
2
200
8
500
7
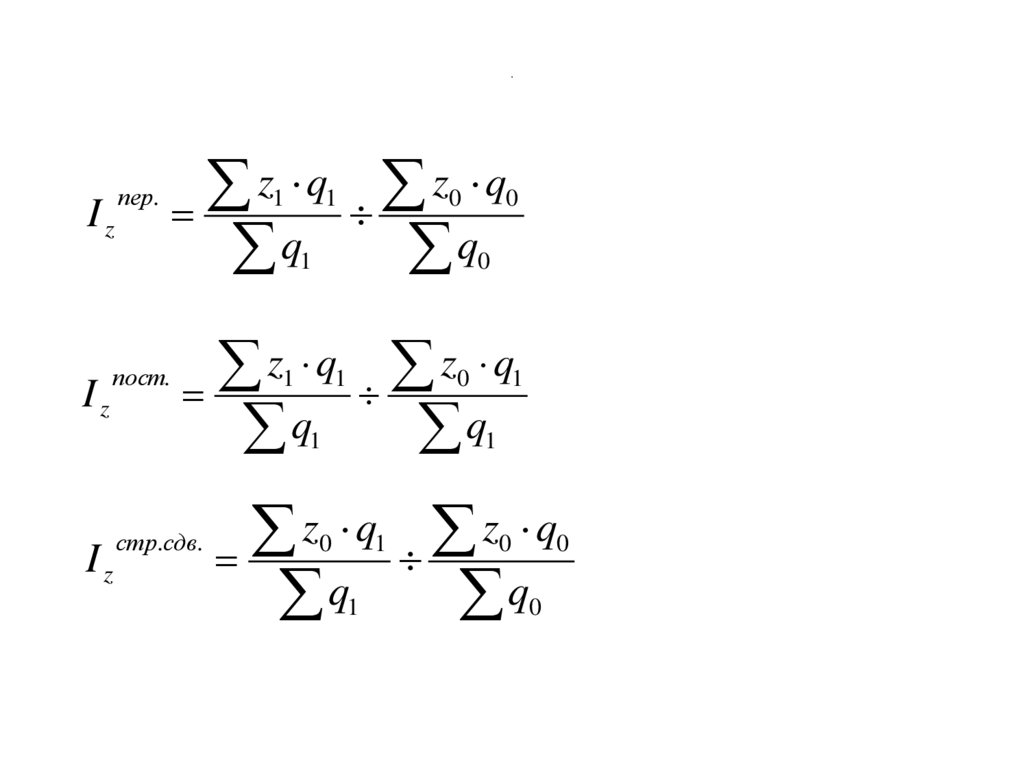
Вычислите индексы себестоимости переменного состава,
постоянного состава и структурных сдвигов
137. .
Izпер.
z q z q
q
q
1
1
0
1
Iz
пост.
0
z q z q
q
q
1
1
0
1
Iz
0
стр.сдв.
1
1
z q z q
q
q
0
1
1
0
0
0
138. .
Izпер.
z q z q
q
q
1
1
0
0
1
Iz
Iz
пер.
0
9 500 7 500 10 500 8 200
8 9,429 0,848
500 500
500 200
пост.
z q z q
q
q
1
1
0
1
Iz
пост.
Iz
.
1
1
10 500 8 500
8
8 9 0,889
500 500
стр.сдв.
z q z q
q
q
0
1
0
1
Iz
стр.сдв.
9 9,429 0,955
0
0
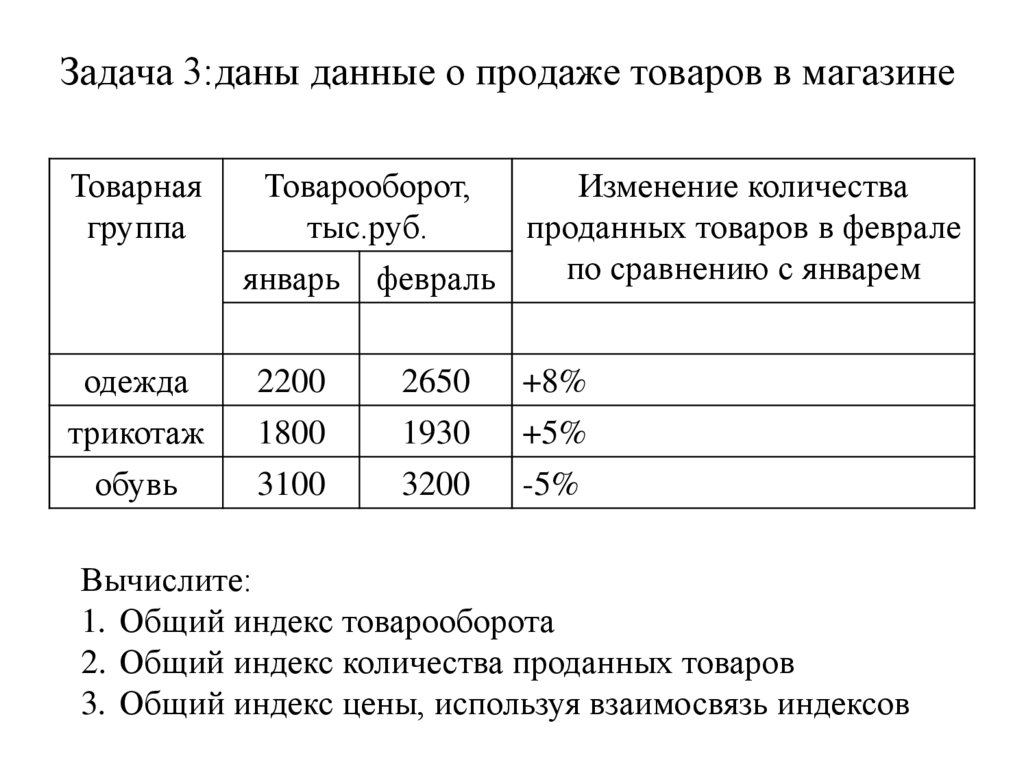
139. Задача 3:даны данные о продаже товаров в магазине
Товарнаягруппа
одежда
трикотаж
обувь
Товарооборот,
Изменение количества
тыс.руб.
проданных товаров в феврале
по сравнению с январем
январь февраль
2200
1800
3100
2650
1930
3200
+8%
+5%
-5%
Вычислите:
1. Общий индекс товарооборота
2. Общий индекс количества проданных товаров
3. Общий индекс цены, используя взаимосвязь индексов
140. .
IТОТО
ТО
1
0
2650 1930 3200 7780
1,096
2200 1800 3100 7100
141. .
I p I q I ТОIТО 1,096
Ip
1,079
I q 1,016
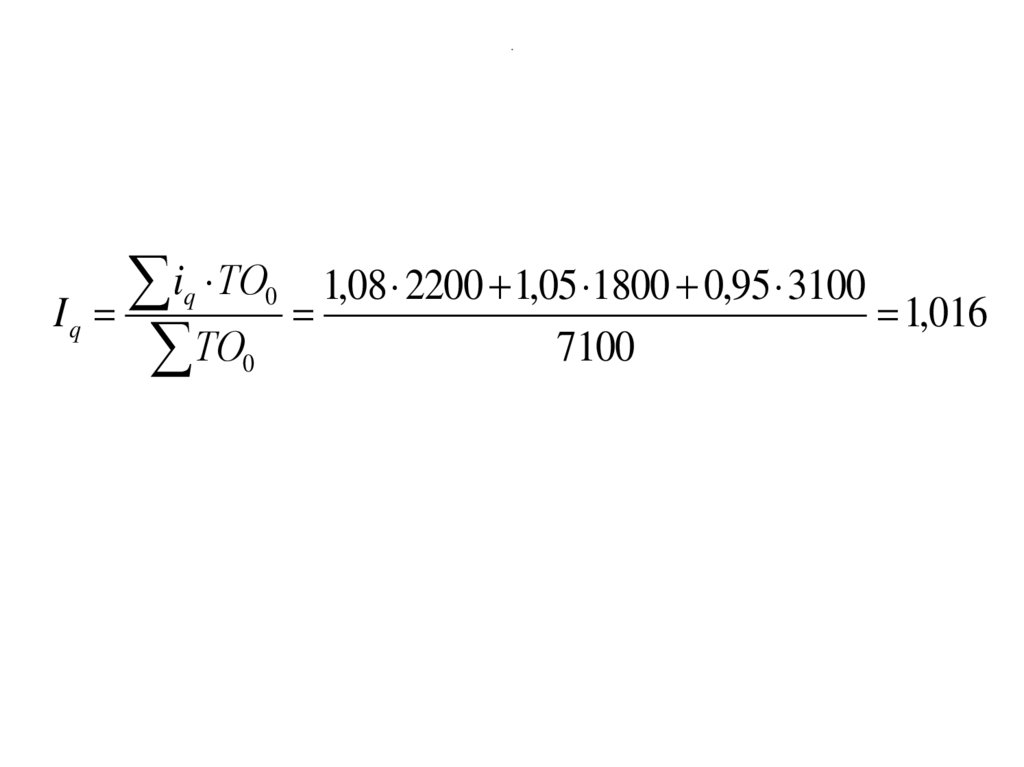
142. .
Iqi ТО
ТО
q
0
0
1,08 2200 1,05 1800 0,95 3100
1,016
7100
143. .
В отчетном периоде посравнению с базисным:
цены выросли на 15%,
товарооборот увеличился на
26,5%.
Как изменилось количество
проданной продукции?
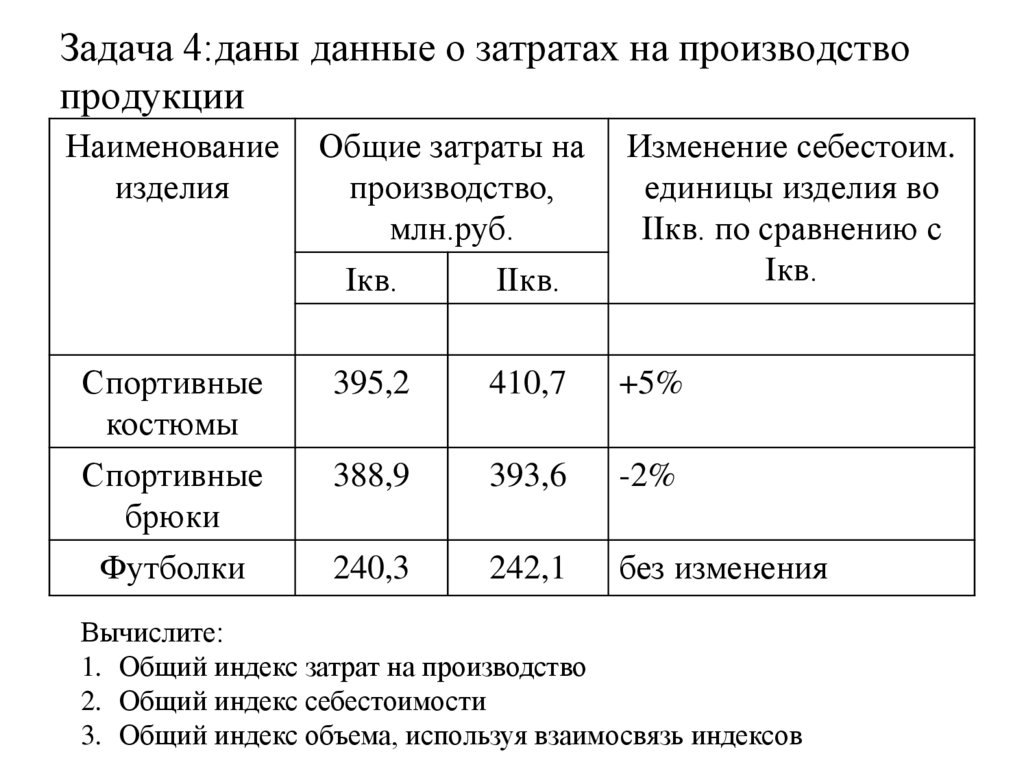
144. Задача 4:даны данные о затратах на производство продукции
Наименованиеизделия
Спортивные
костюмы
Спортивные
брюки
Футболки
Общие затраты на
производство,
млн.руб.
Iкв.
IIкв.
Изменение себестоим.
единицы изделия во
IIкв. по сравнению с
Iкв.
395,2
410,7
+5%
388,9
393,6
-2%
240,3
242,1
без изменения
Вычислите:
1. Общий индекс затрат на производство
2. Общий индекс себестоимости
3. Общий индекс объема, используя взаимосвязь индексов
145. .
IЗЗ
З
1
0
Iz
З
З
i
1
1
z
410,7 393,6 242,1 1046,4
1,021
395,2 388,9 240,3 1024,4
1046,4
1046,4
1,011
410,7 393,6 242,1 1034,8
1,05
0,98
1
I З 1,021
Iq
1,01
I z 1,011














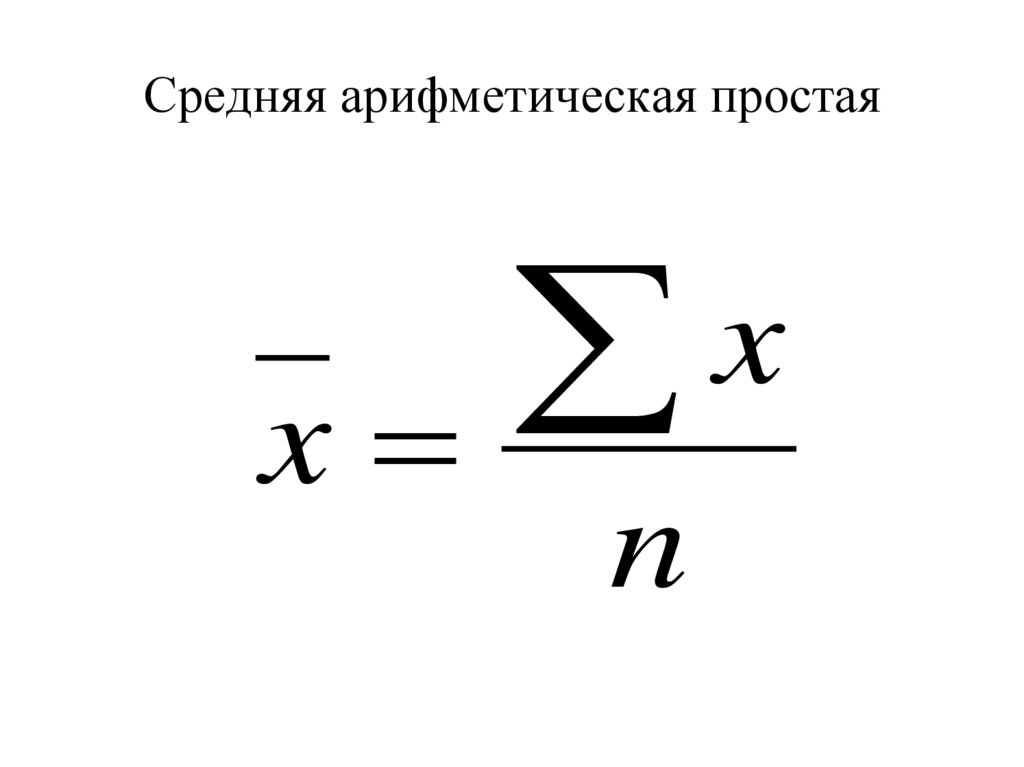

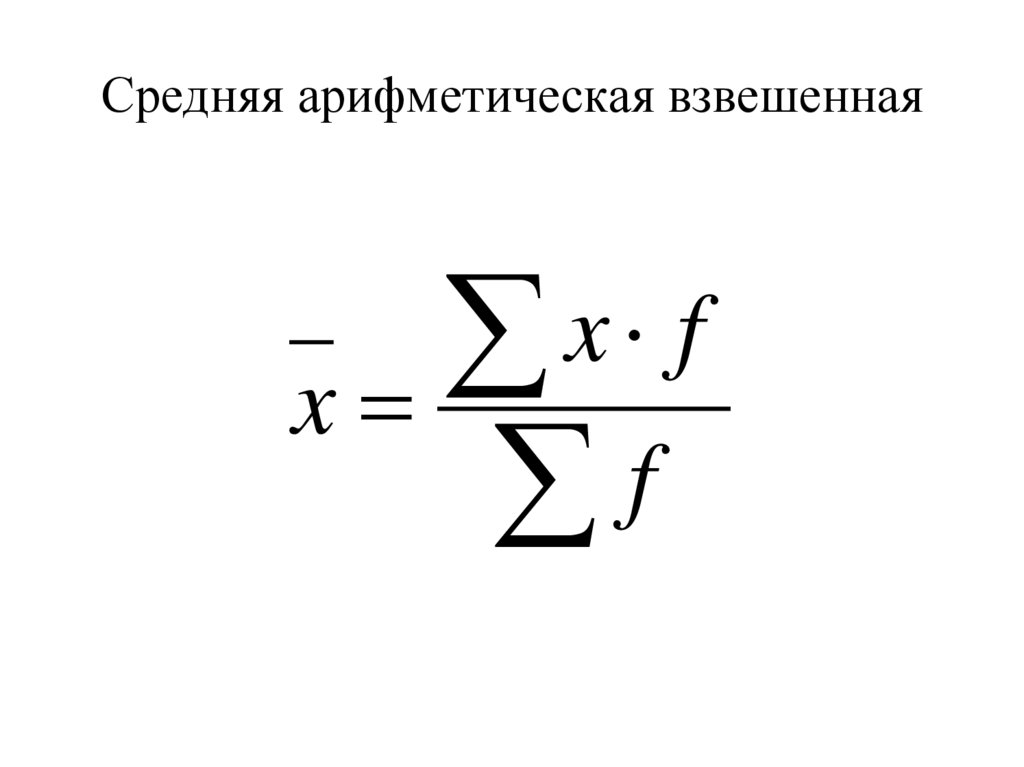
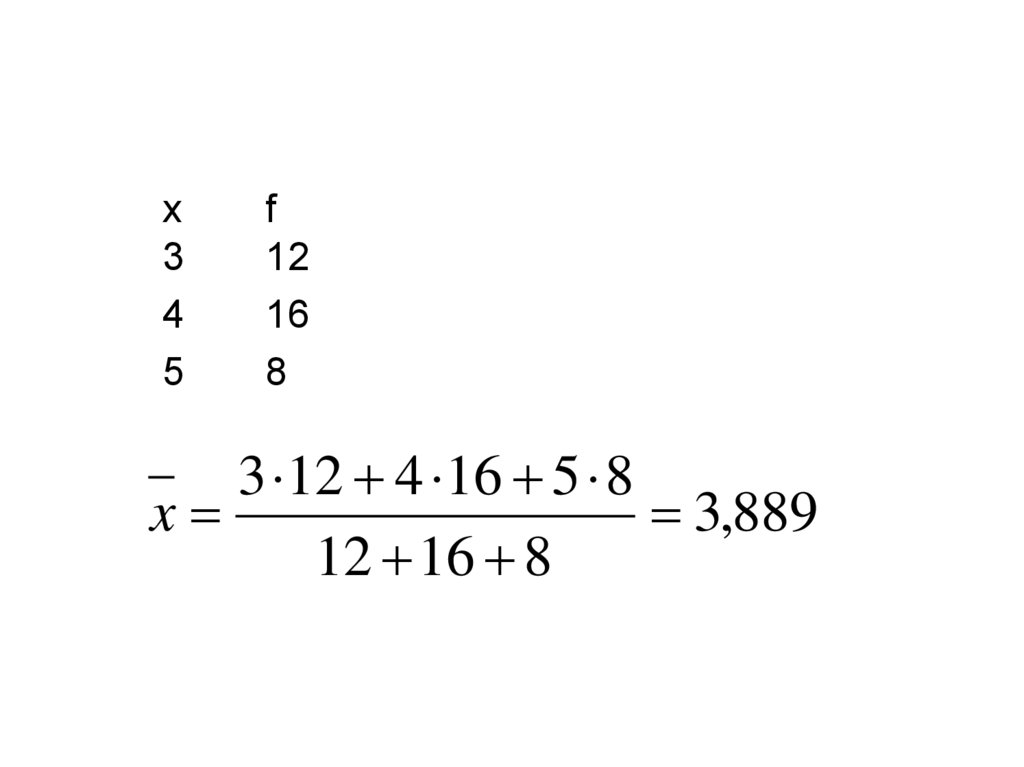













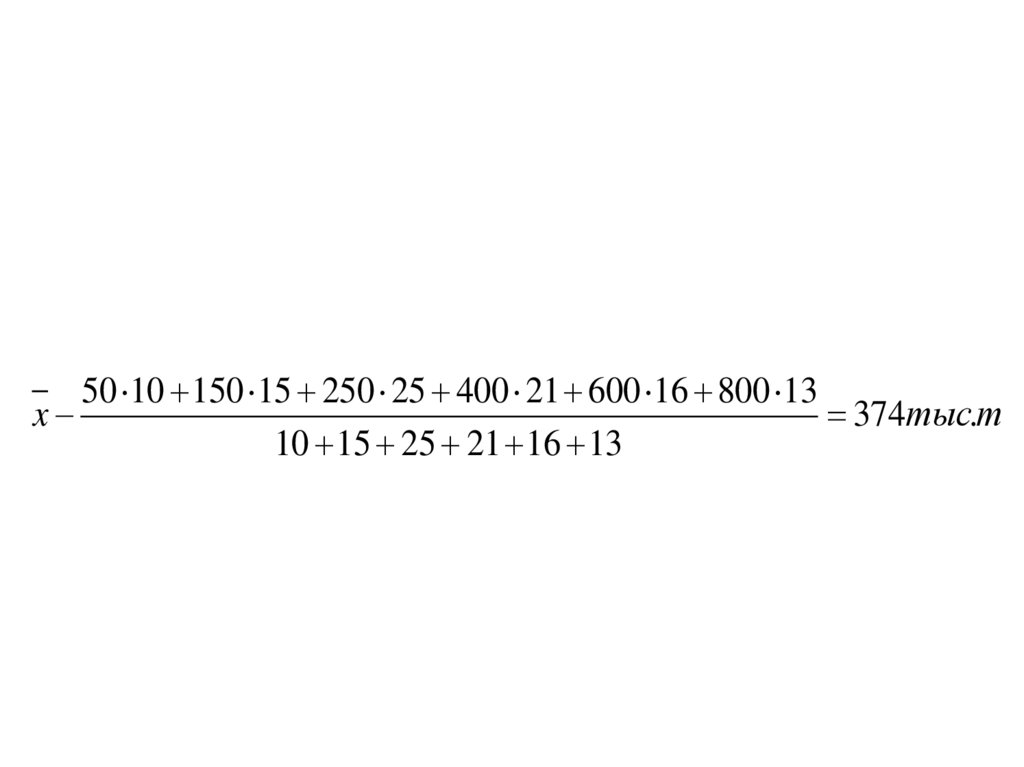





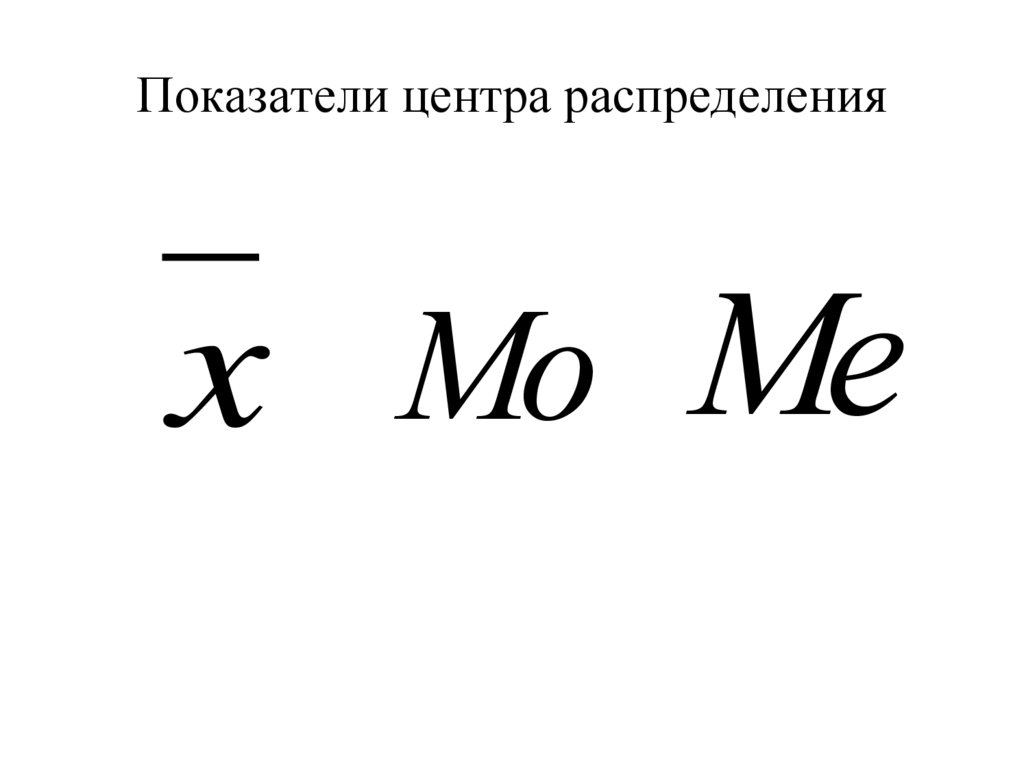



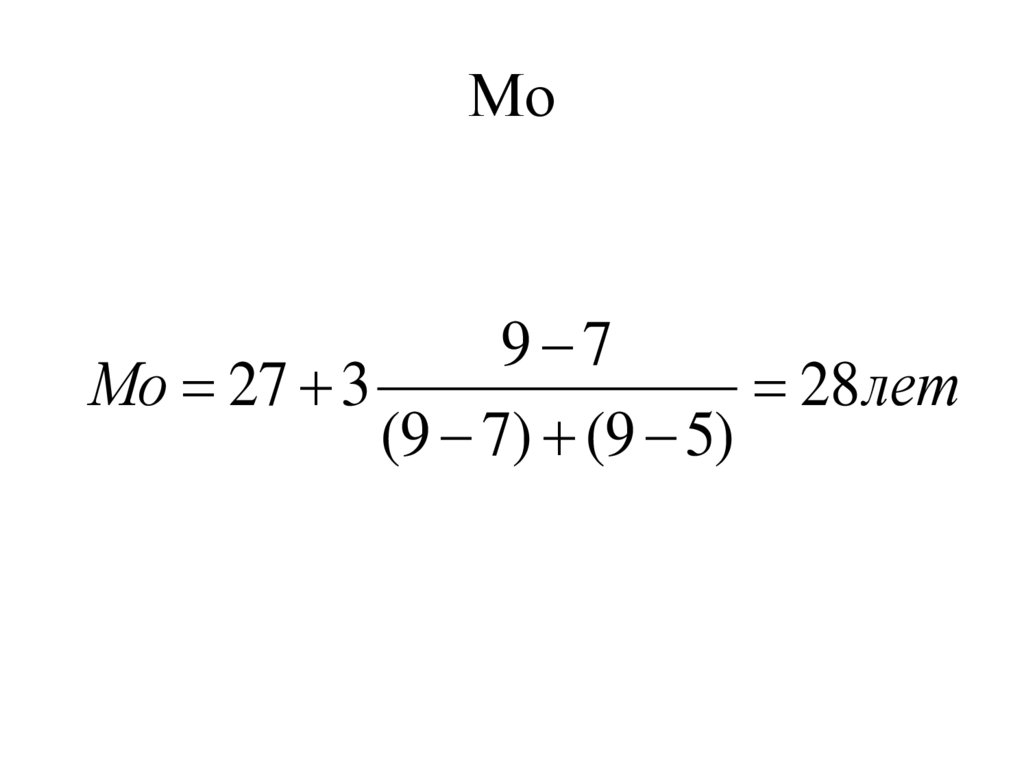



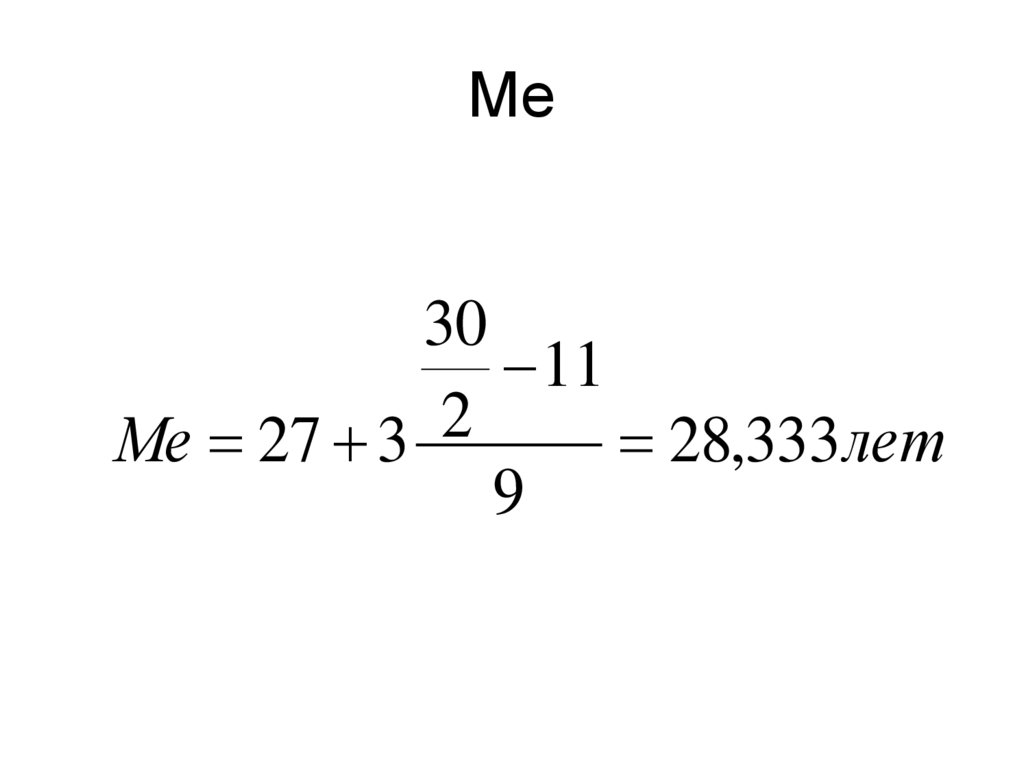
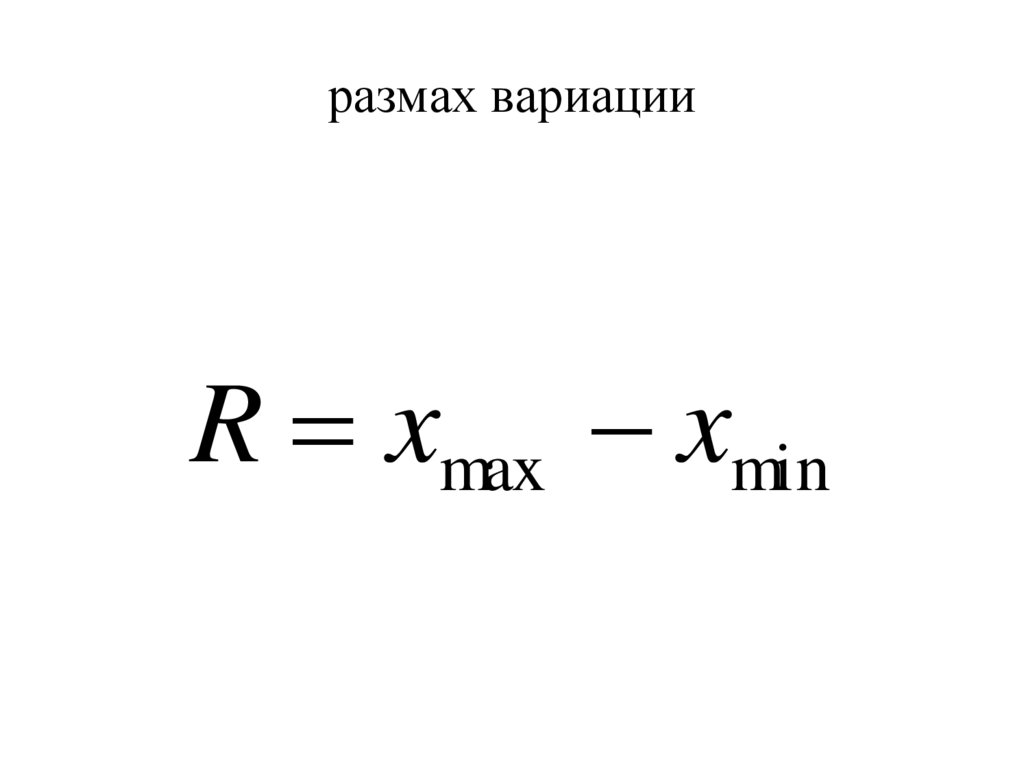

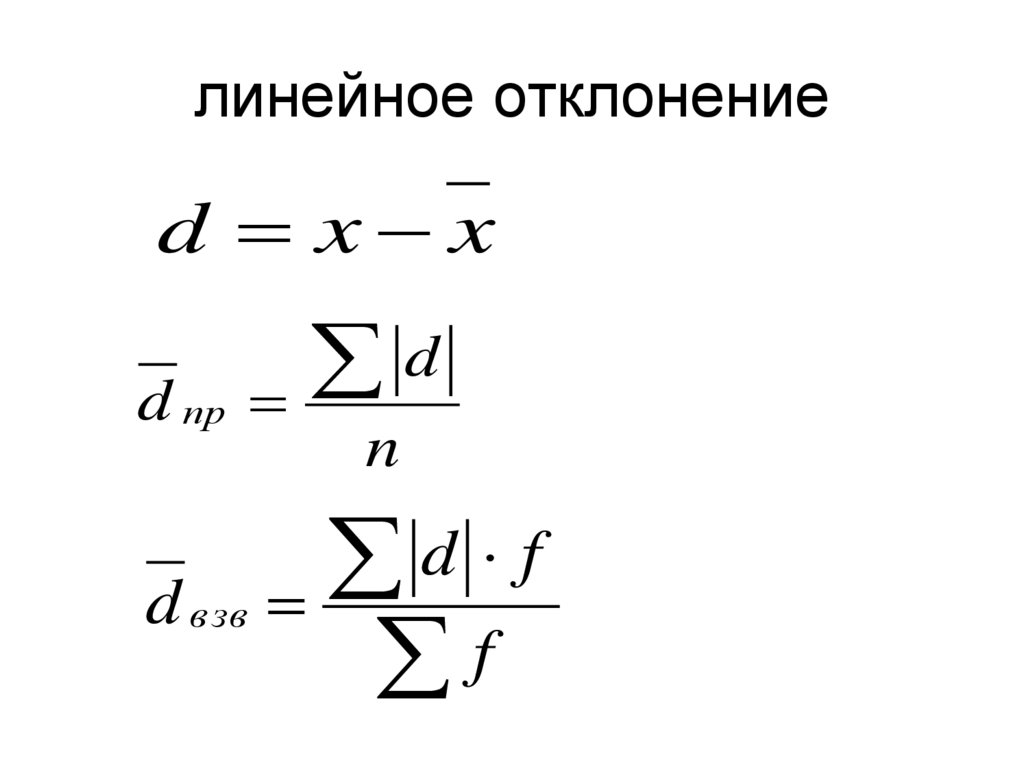

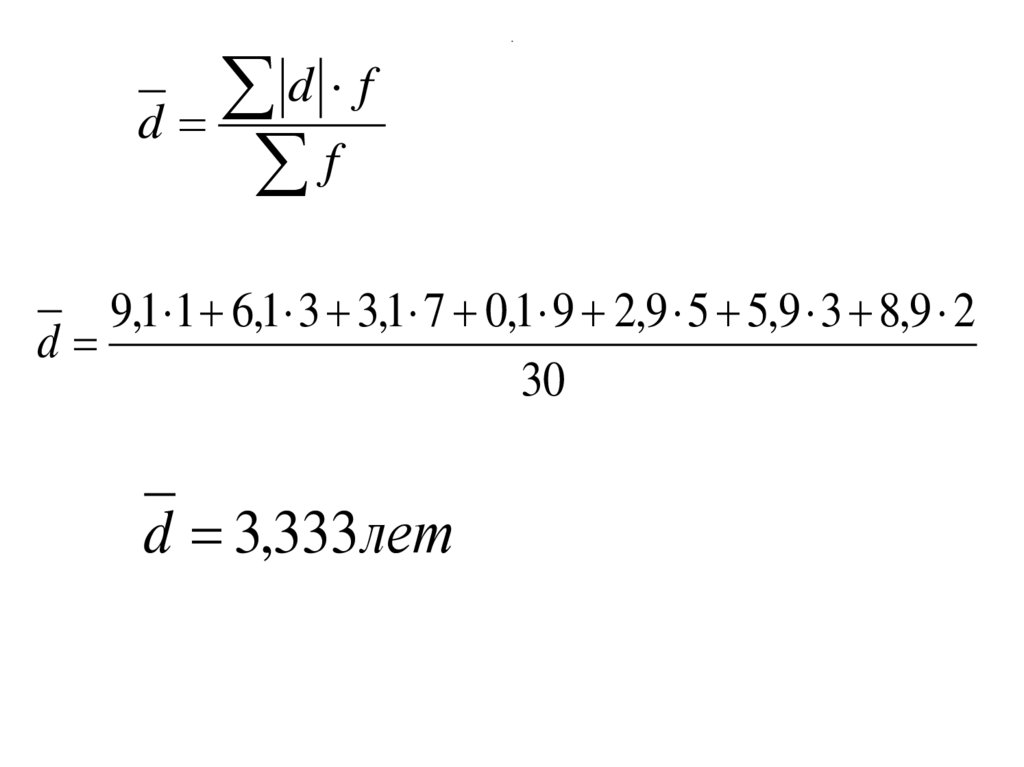



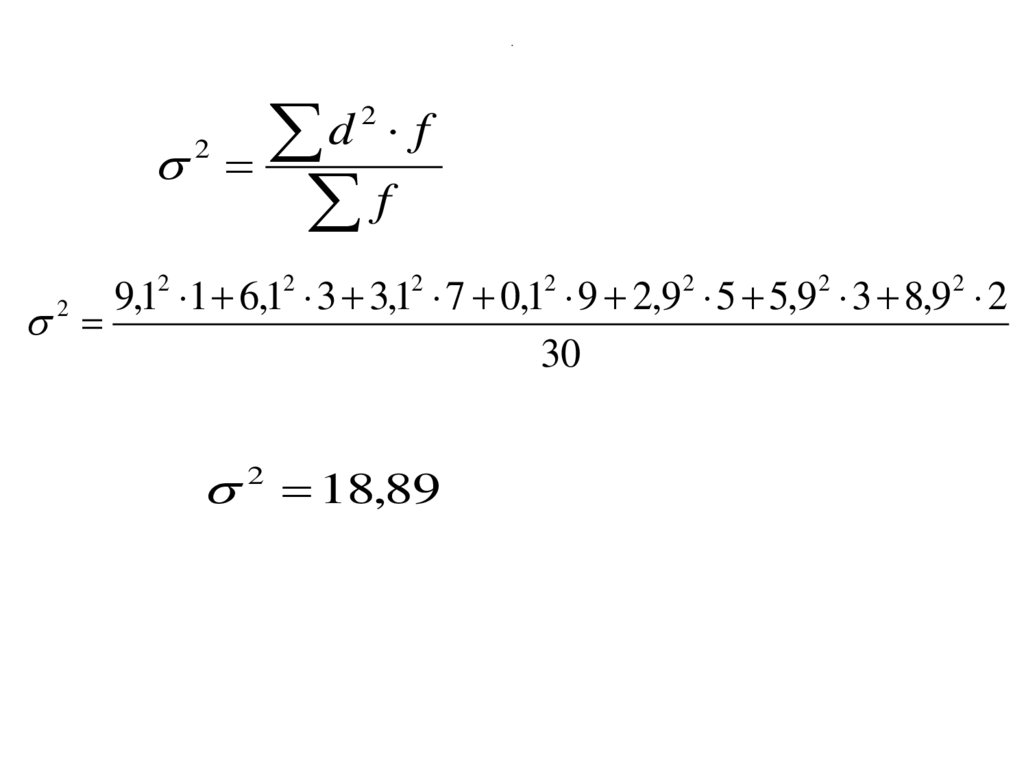










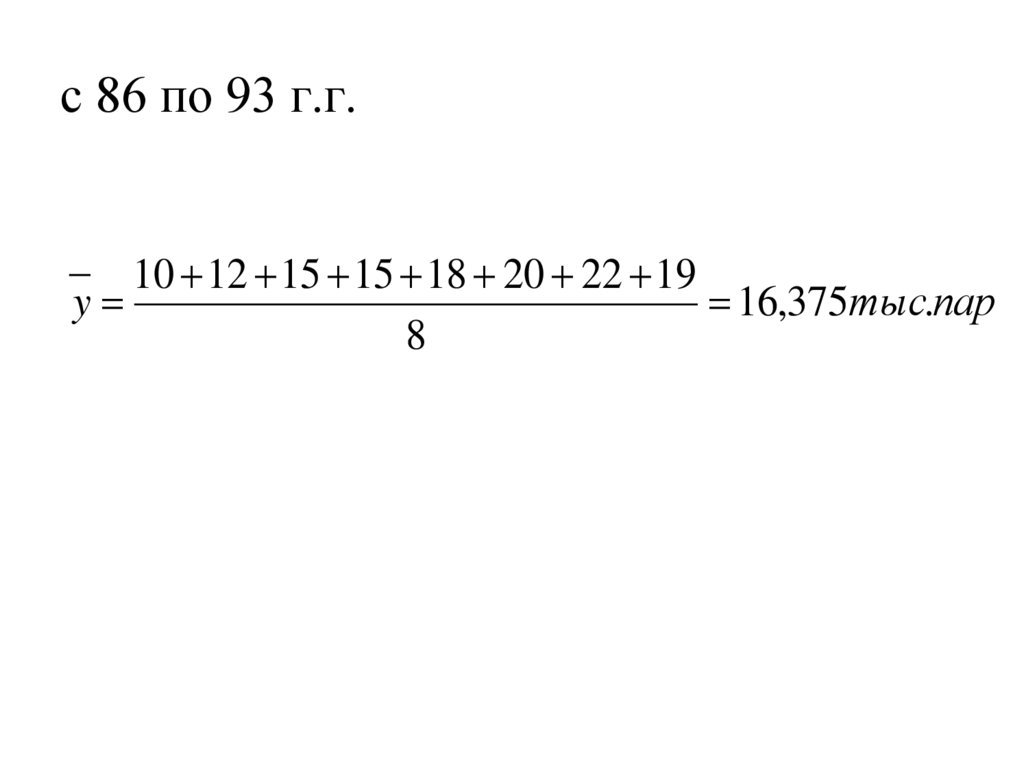





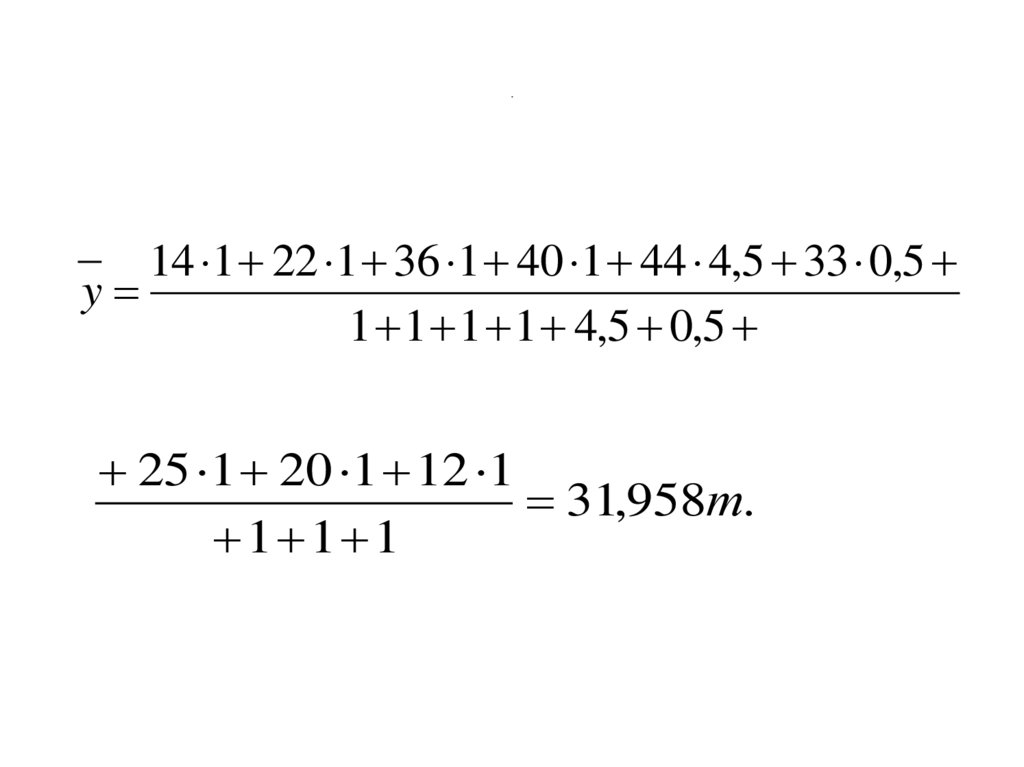
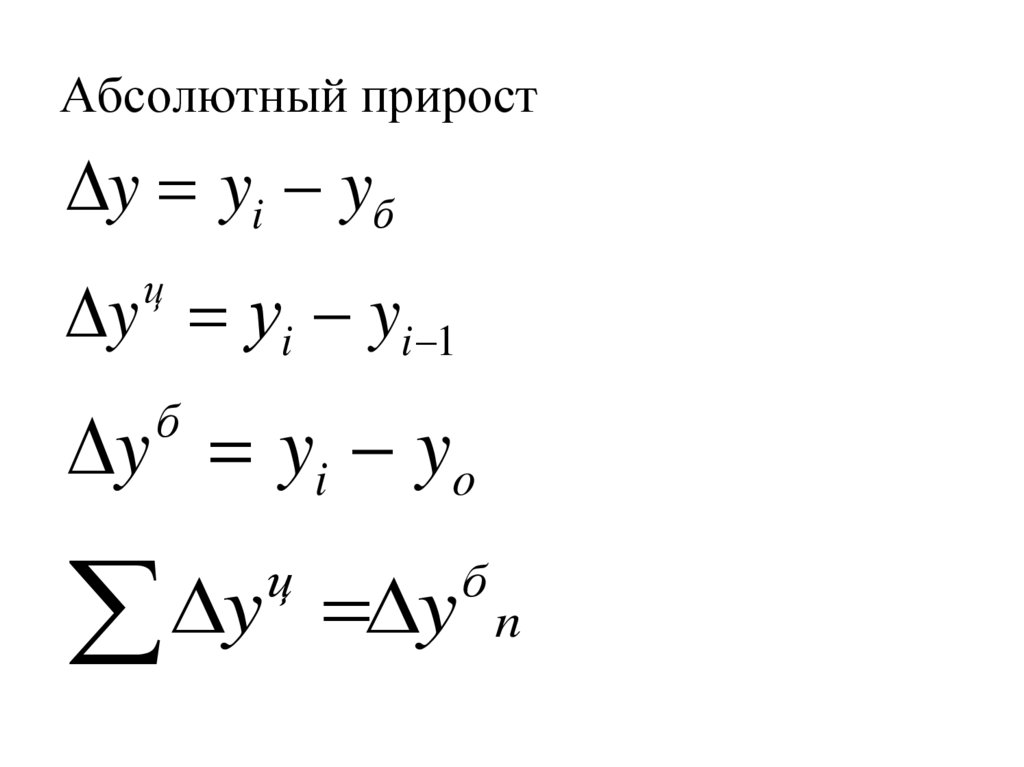













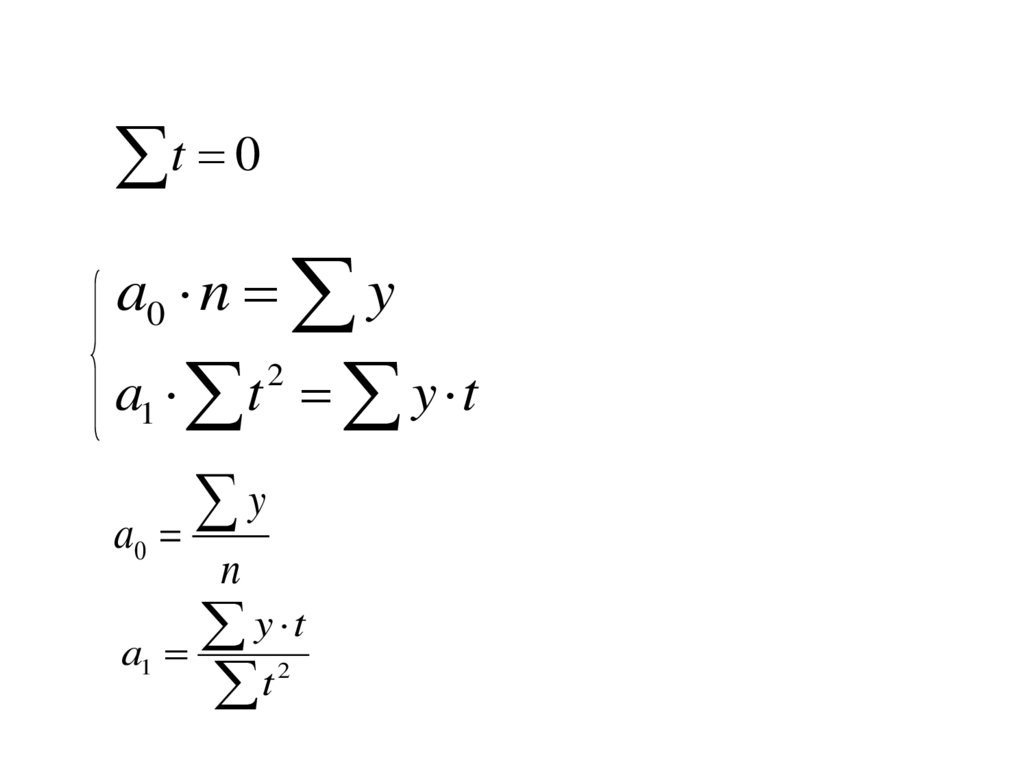



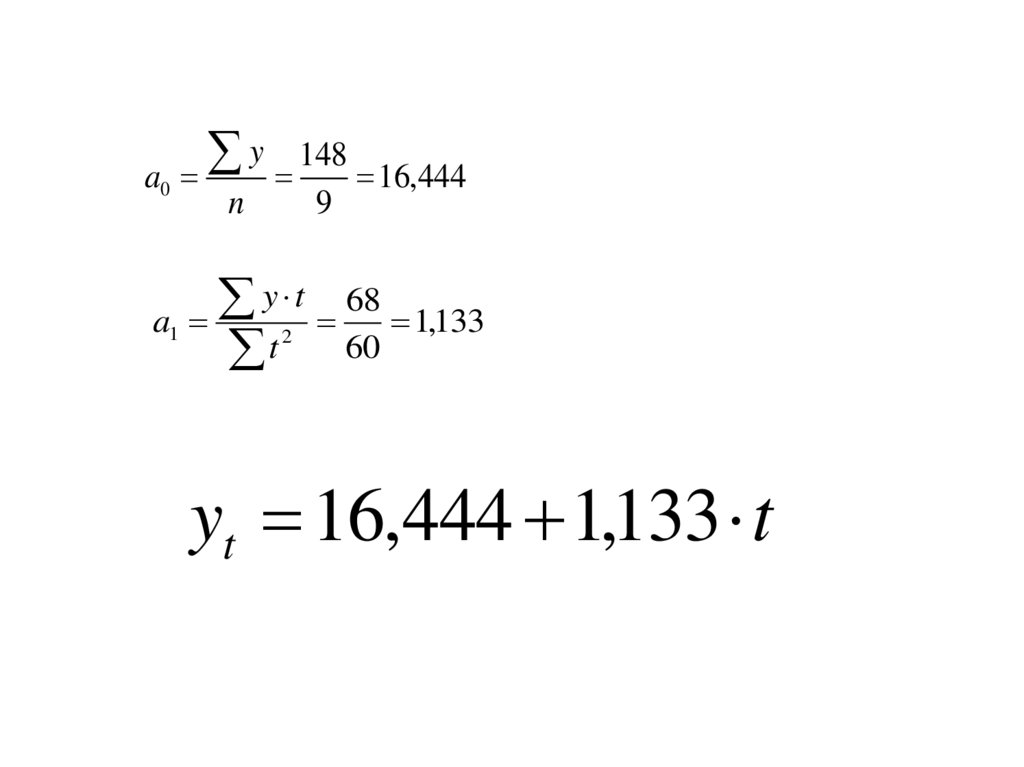


















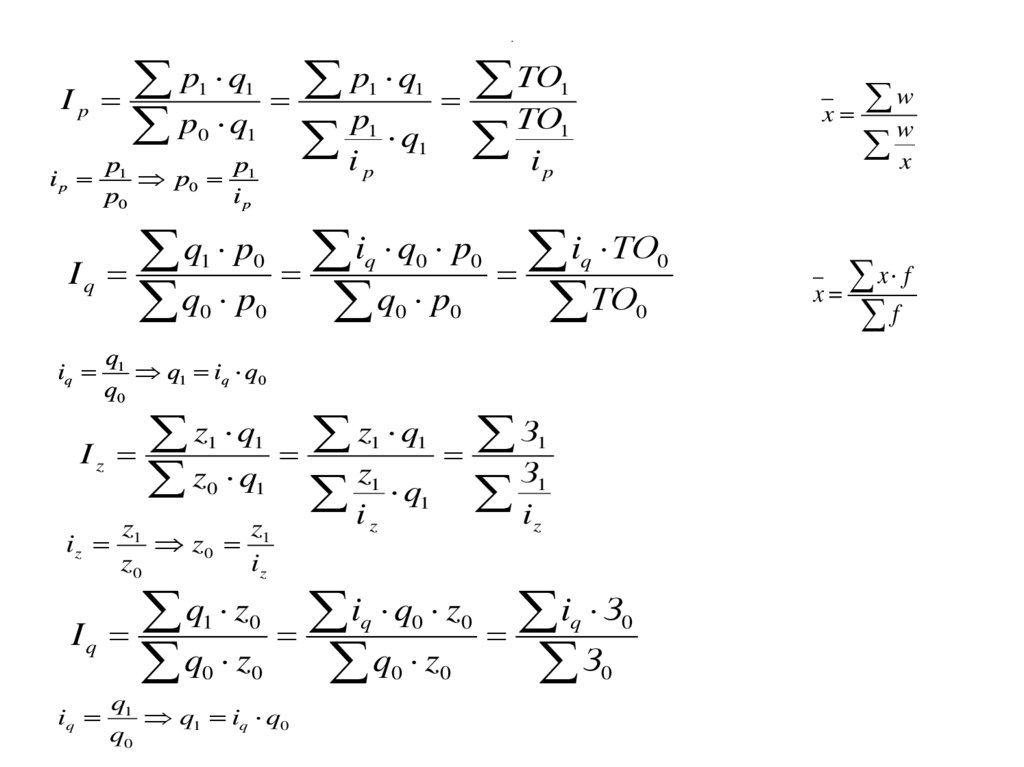


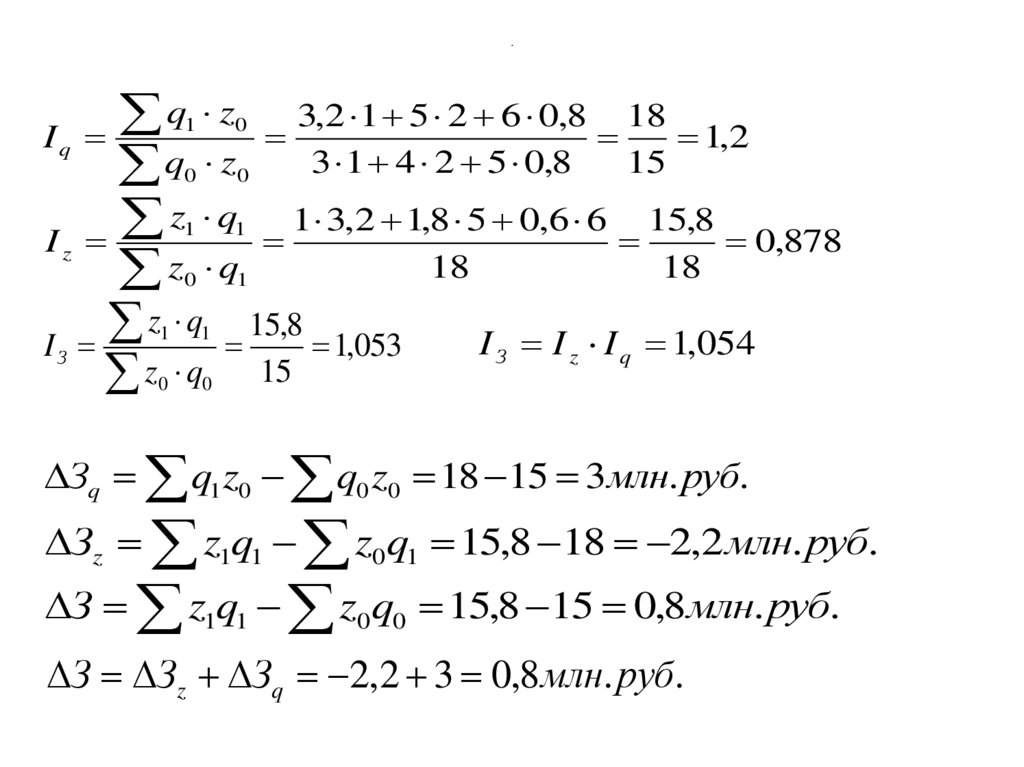





 Математика
Математика








