Похожие презентации:
Побудова перерізів многогранників
1.
Побудоваперерізів
многогранників
2.
1. Переріз куба2. Переріз піраміди
3. Переріз призми
3.
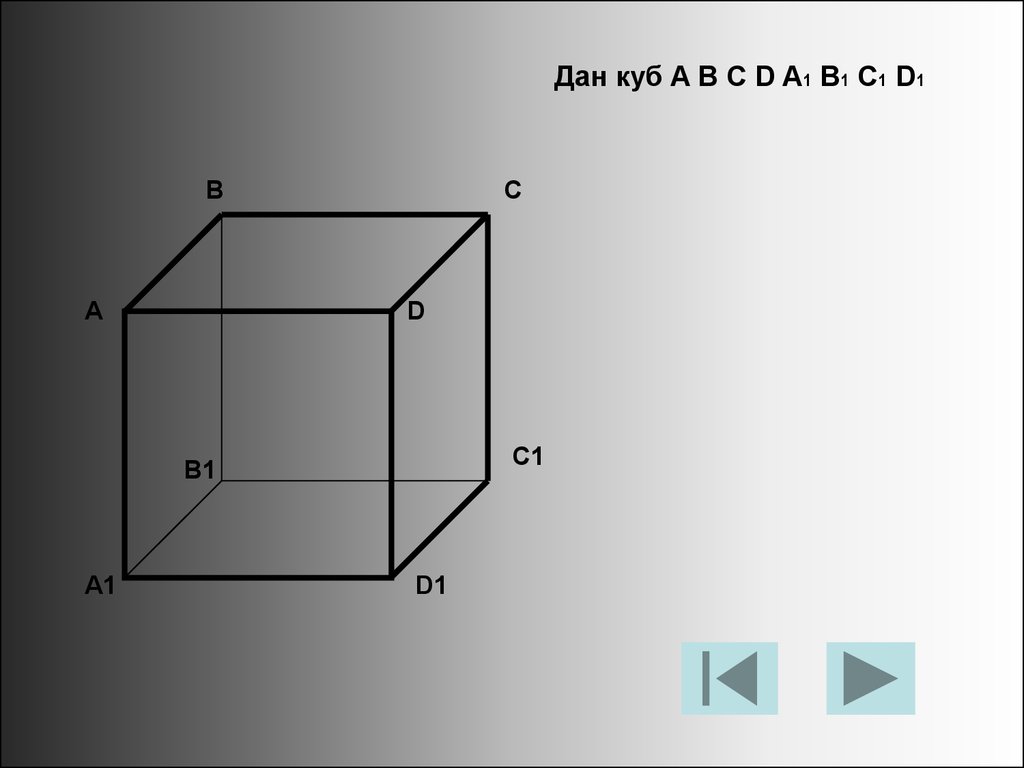
Дан куб A B C D A1 B1 C1 D1В
А
С
D
C1
B1
A1
D1
4.
ВС
А
D
B1
C1
P
R
A1
Q
D1
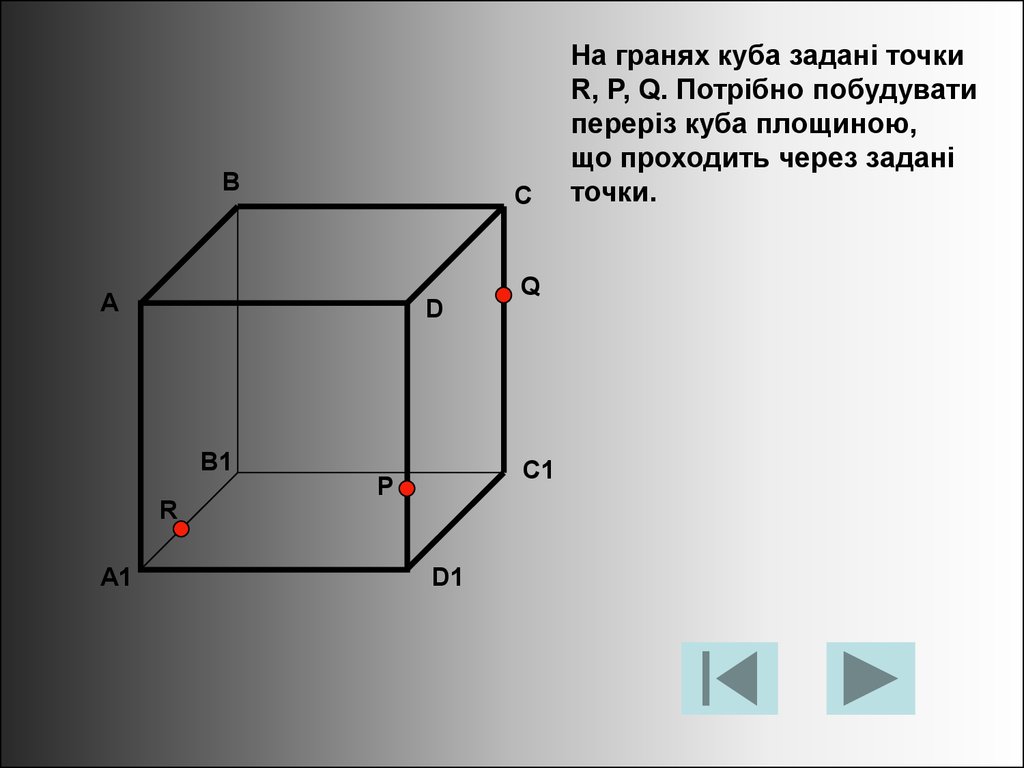
На гранях куба задані точки
R, P, Q. Потрібно побудувати
переріз куба площиною,
що проходить через задані
точки.
5.
ВС
А
D
B1
C1
P
R
A1
Q
D1
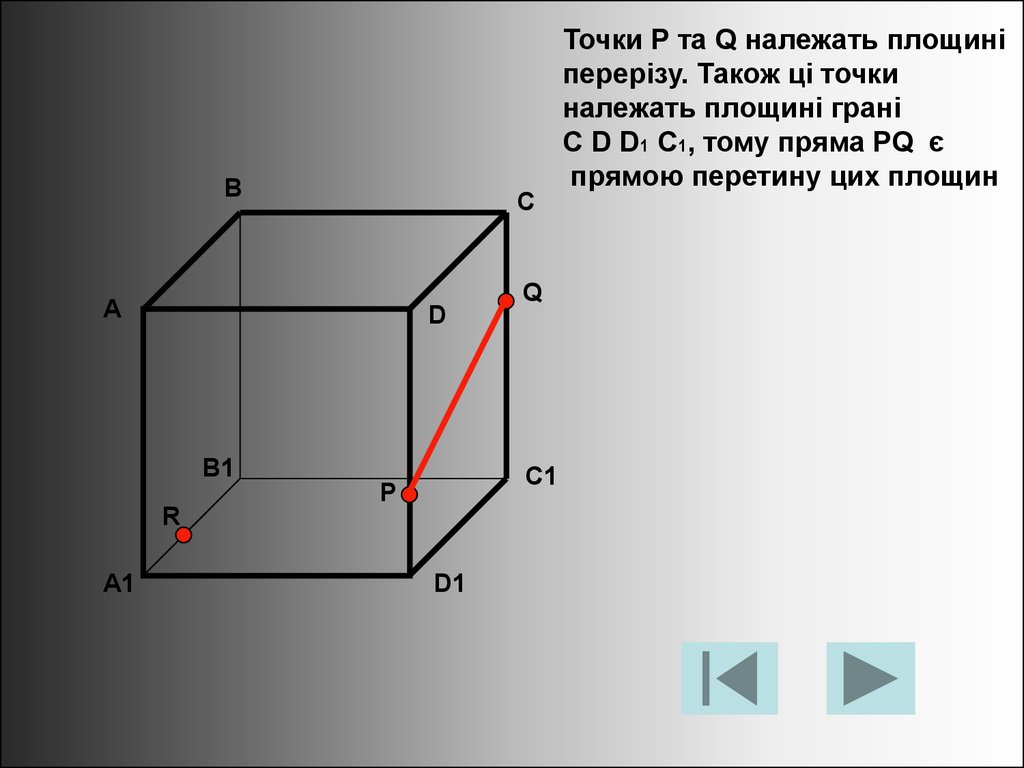
Точки Р та Q належать площині
перерізу. Також ці точки
належать площині грані
C D D1 C1, тому пряма PQ є
прямою перетину цих площин
6.
ВС
А
D
B1
C1
P
R
A1
D1
E
Q
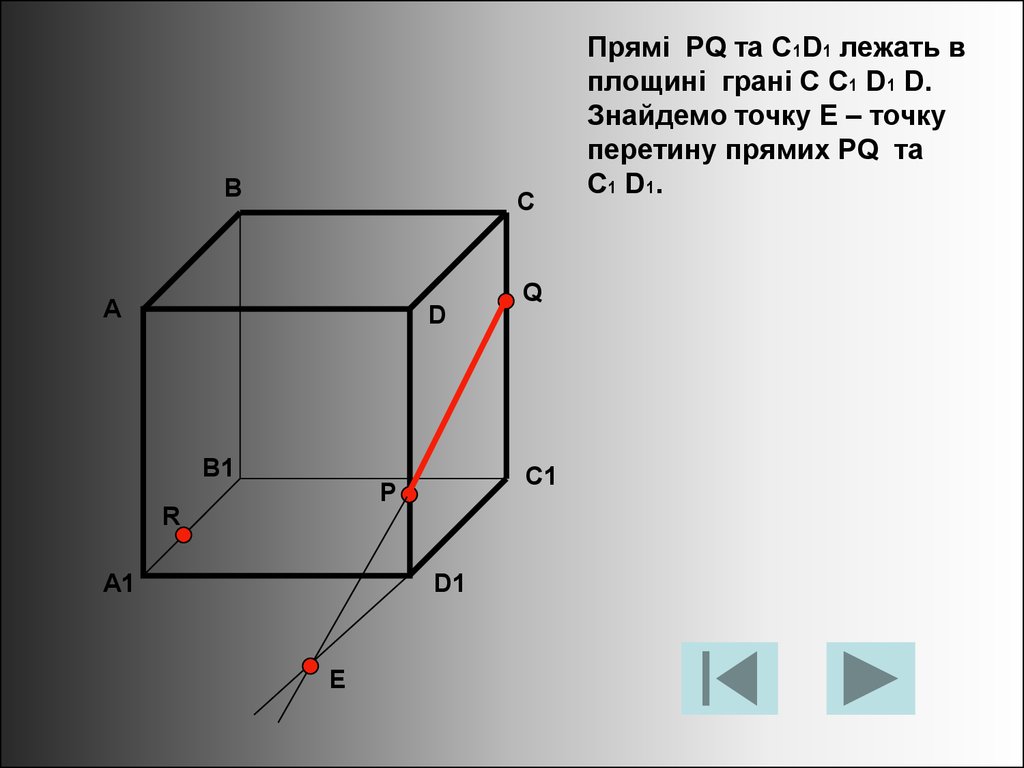
Прямі PQ та C1D1 лежать в
площині грані C C1 D1 D.
Знайдемо точку Е – точку
перетину прямих PQ та
C1 D1.
7.
ВС
А
D
B1
C1
P
R
A1
D1
E
Q
Точки R та E належать
площині перерізу та площині
основи куба, тому пряма RE,
що з’єднує ці точки, є прямою
перетину площини перерізу
та площини основи куба .
8.
ВС
А
D
B1
C1
P
R
A1
D1
F
E
Q
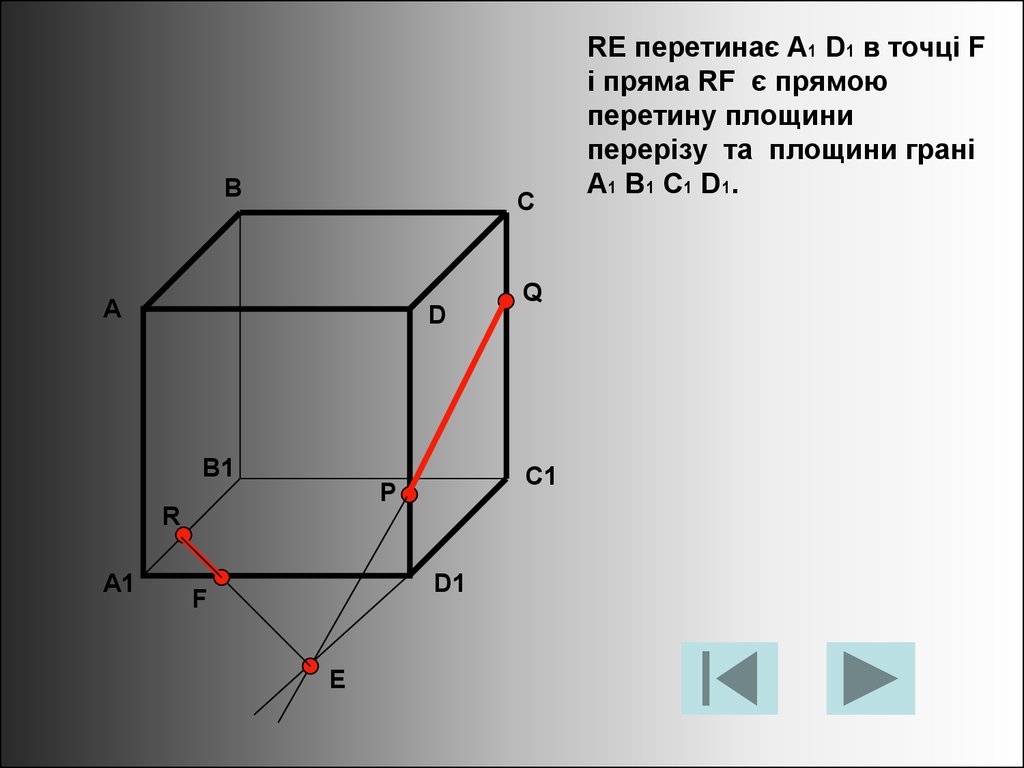
RE перетинає A1 D1 в точці F
і пряма RF є прямою
перетину площини
перерізу та площини грані
A1 B1 C1 D1.
9.
ВС
А
D
B1
P
C1
Q
R
A1
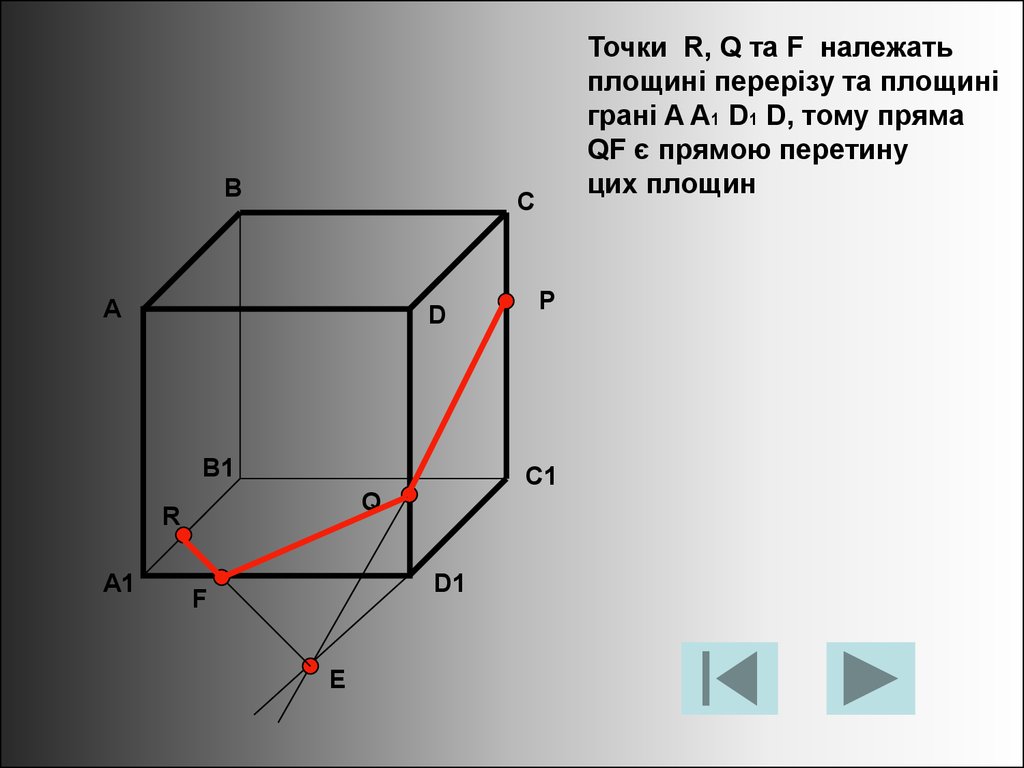
Точки R, Q та F належать
площині перерізу та площині
грані A A1 D1 D, тому пряма
QF є прямою перетину
цих площин
D1
F
E
10.
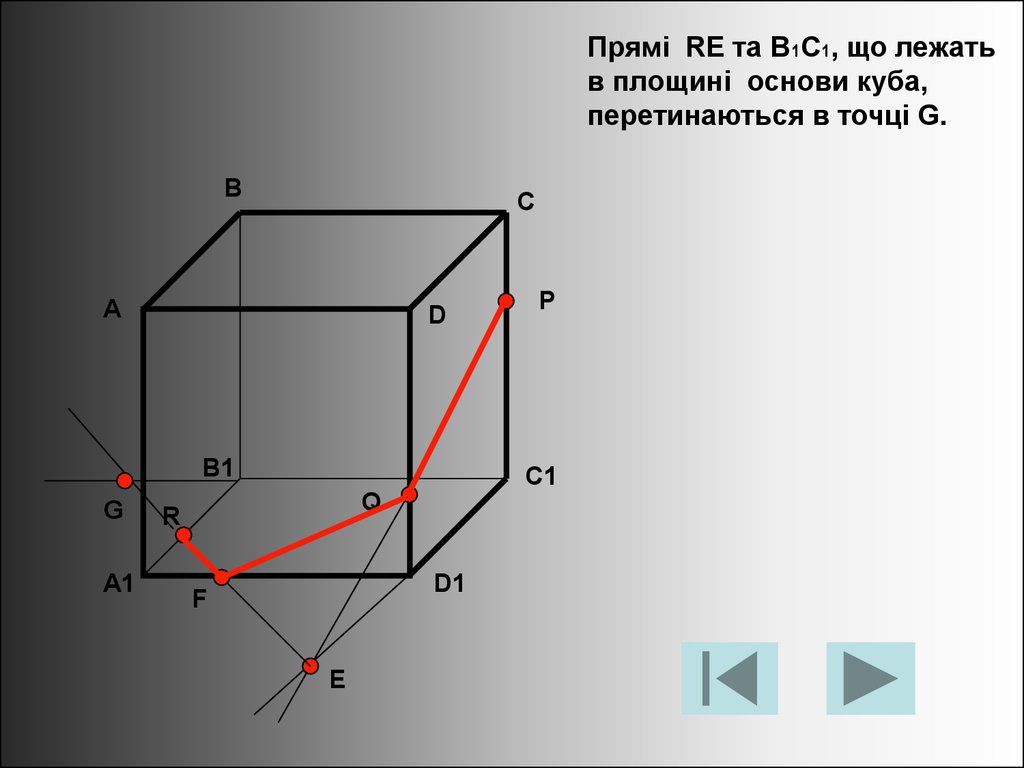
Прямі RE та B1C1, що лежатьв площині основи куба,
перетинаються в точці G.
В
С
А
D
B1
G
A1
P
C1
Q
R
D1
F
E
11.
ВС
А
D
B1
G
A1
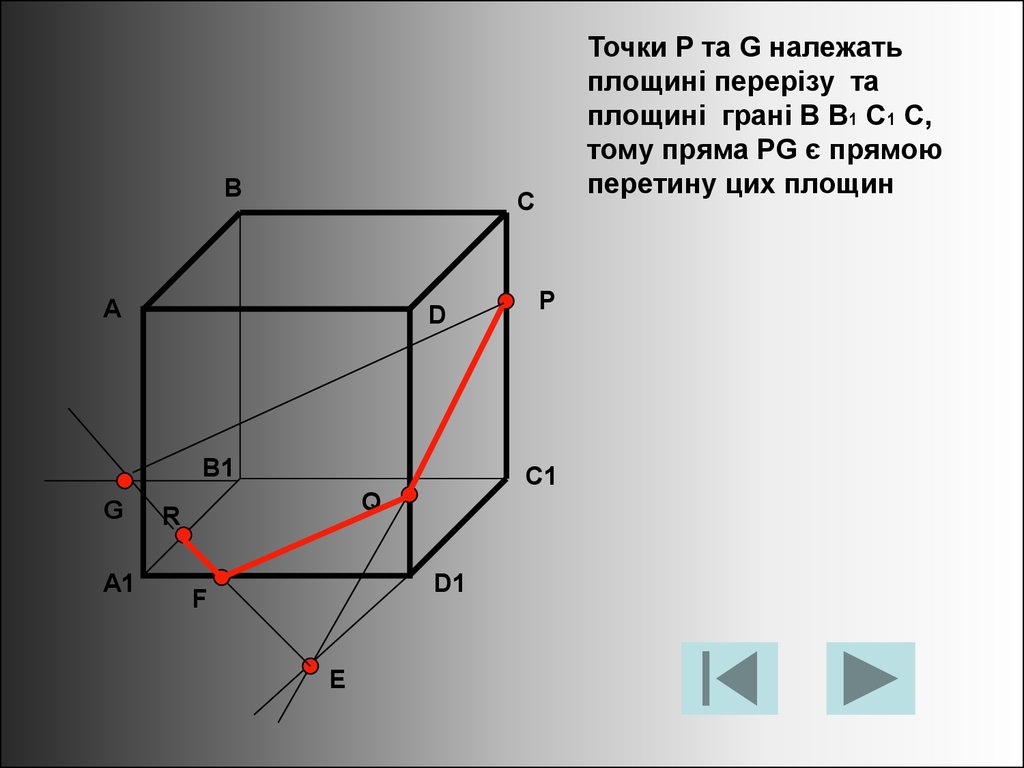
Точки P та G належать
площині перерізу та
площині грані B B1 C1 C,
тому пряма PG є прямою
перетину цих площин
P
C1
Q
R
D1
F
E
12.
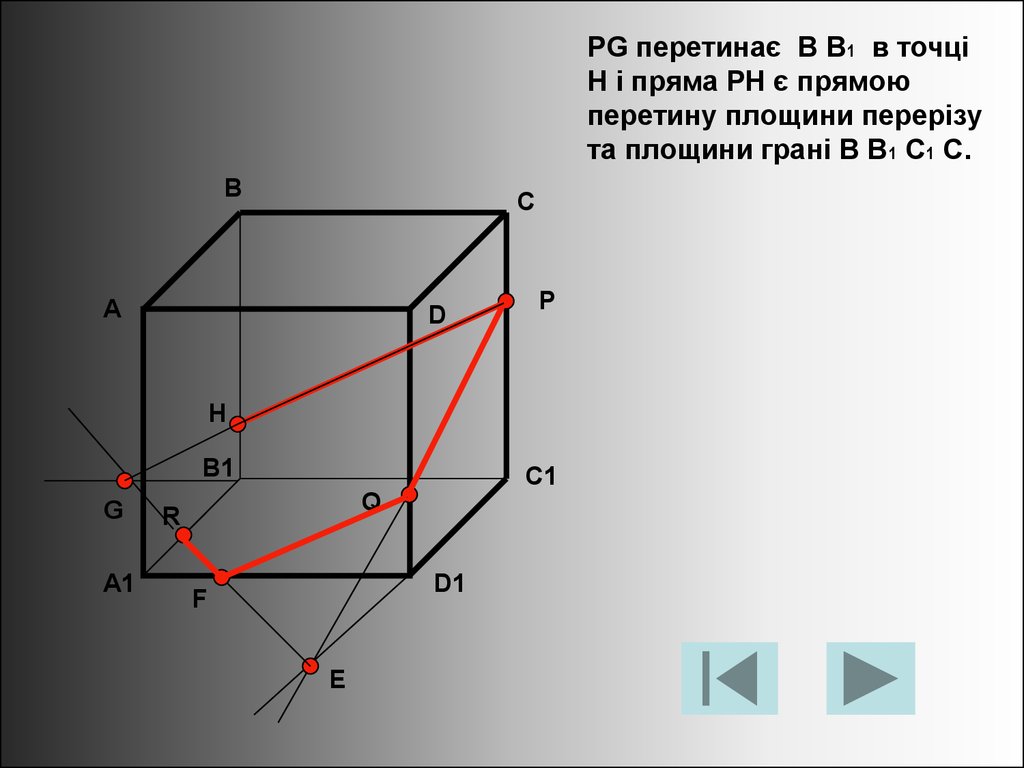
PG перетинає B B1 в точціH і пряма PH є прямою
перетину площини перерізу
та площини грані B B1 C1 C.
В
С
А
D
P
H
B1
G
A1
C1
Q
R
D1
F
E
13.
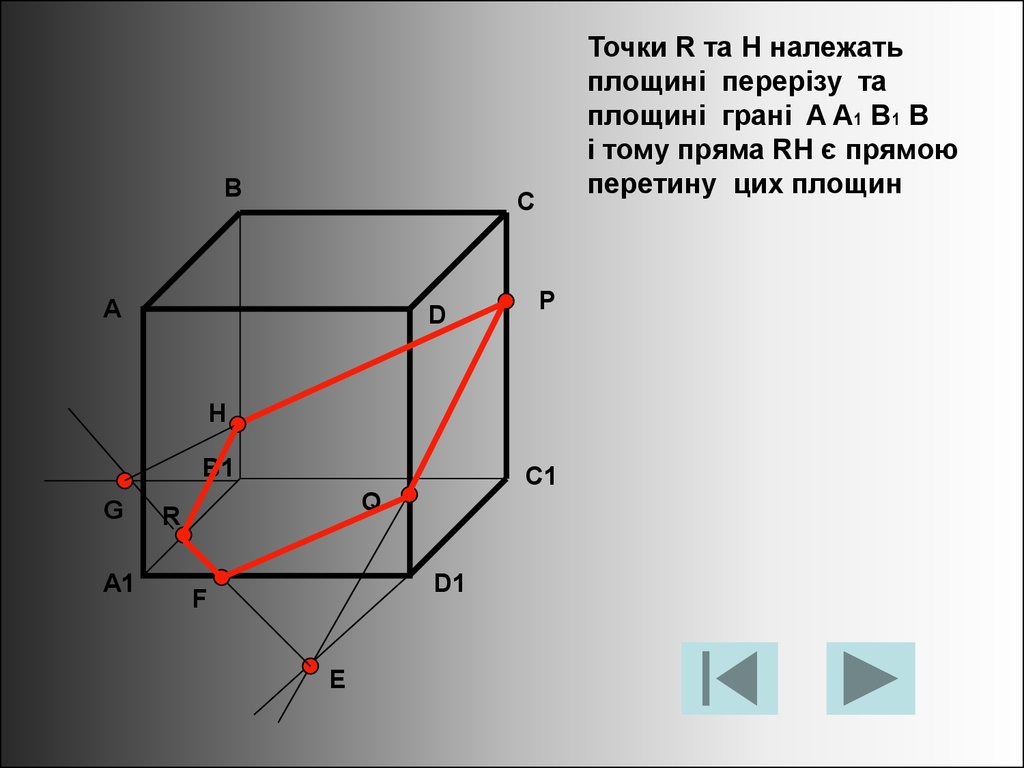
ВТочки R та H належать
площині перерізу та
площині грані A A1 B1 B
і тому пряма RH є прямою
перетину цих площин
С
А
D
P
H
B1
G
A1
C1
Q
R
D1
F
E
14.
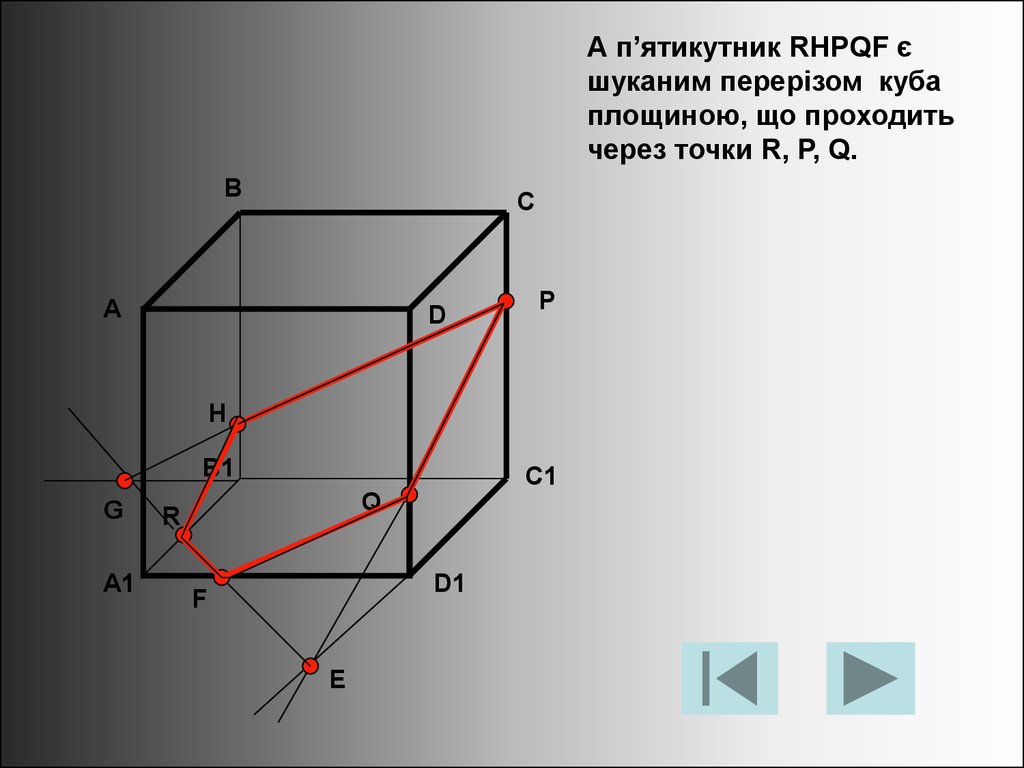
А п’ятикутник RHPQF єшуканим перерізом куба
площиною, що проходить
через точки R, P, Q.
В
С
А
D
P
H
B1
G
A1
C1
Q
R
D1
F
E
15.
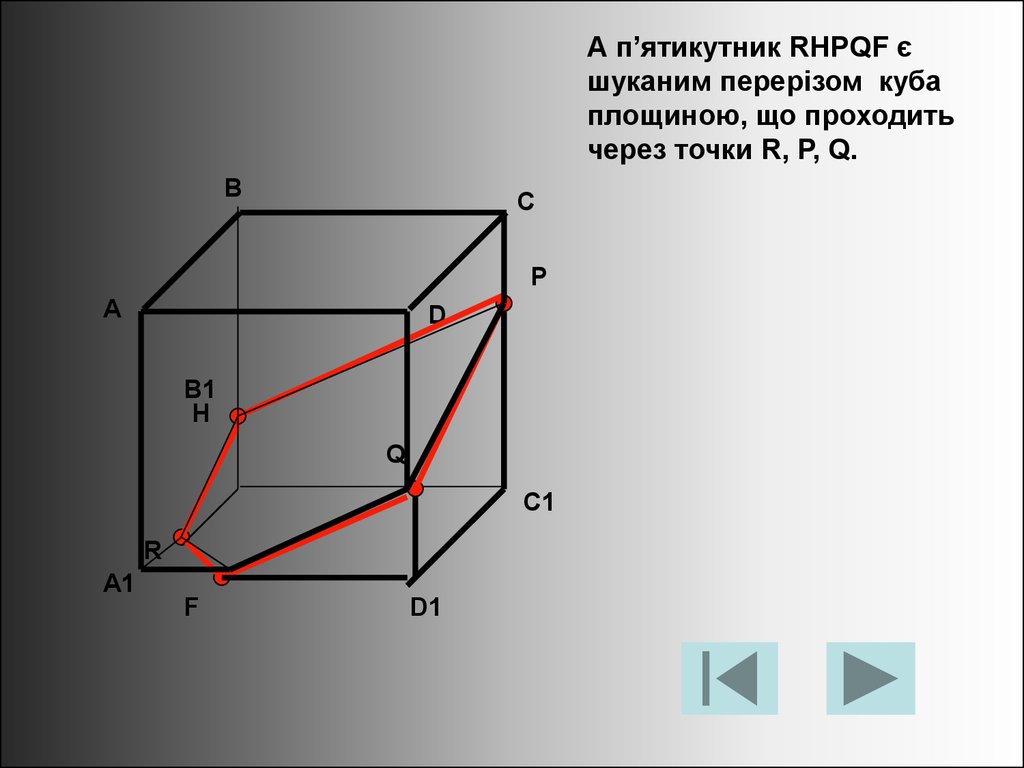
А п’ятикутник RHPQF єшуканим перерізом куба
площиною, що проходить
через точки R, P, Q.
В
С
P
А
D
B1
H
Q
C1
R
A1
F
D1
16.
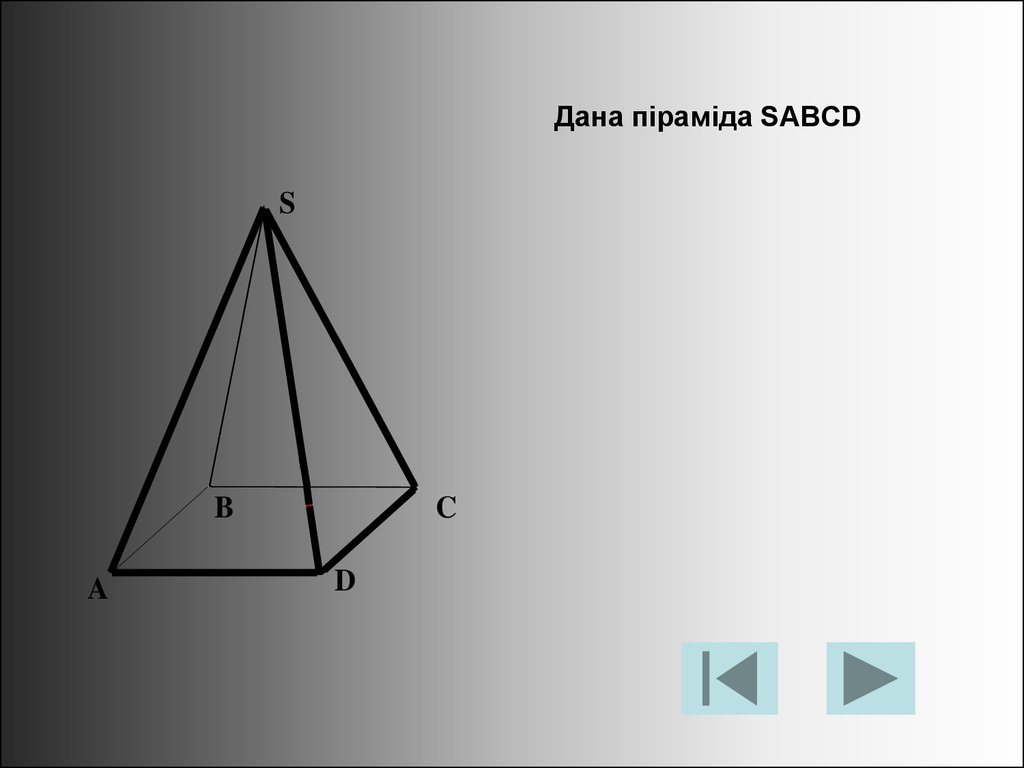
Дана піраміда SABCDS
B
A
C
D
17.
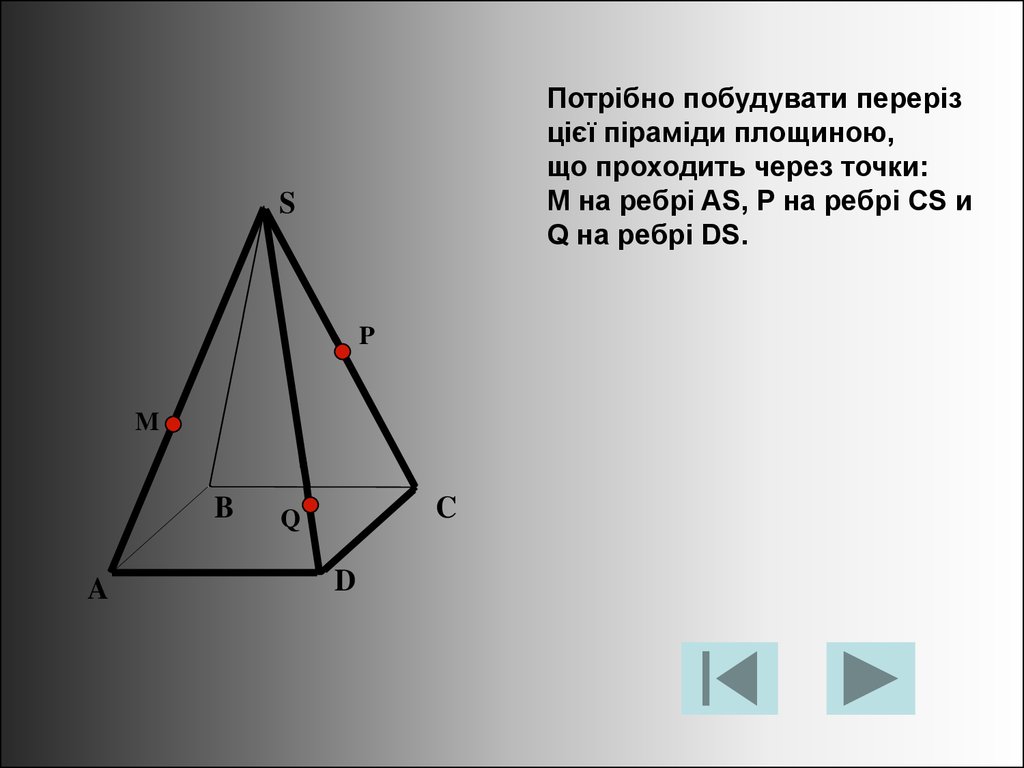
Потрібно побудувати перерізцієї піраміди площиною,
що проходить через точки:
М на ребрі AS, P на ребрі CS и
Q на ребрі DS.
S
P
M
B
A
C
Q
D
18.
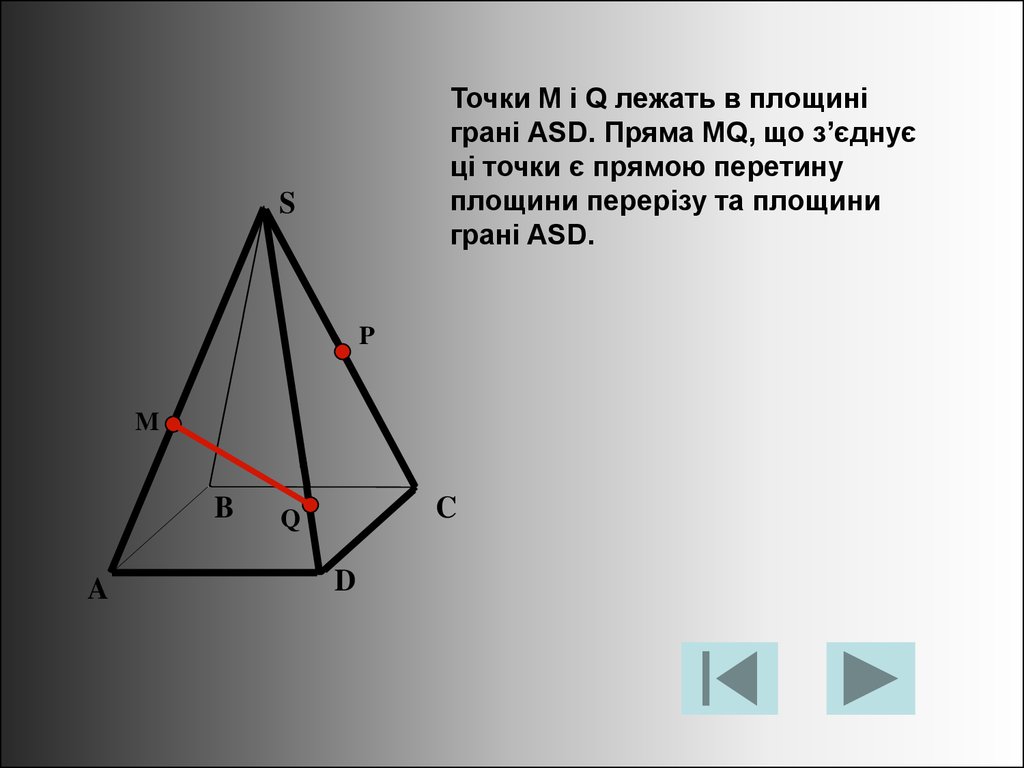
Точки M і Q лежать в площиніграні АSD. Пряма МQ, що з’єднує
ці точки є прямою перетину
площини перерізу та площини
грані ASD.
S
P
M
B
A
C
Q
D
19.
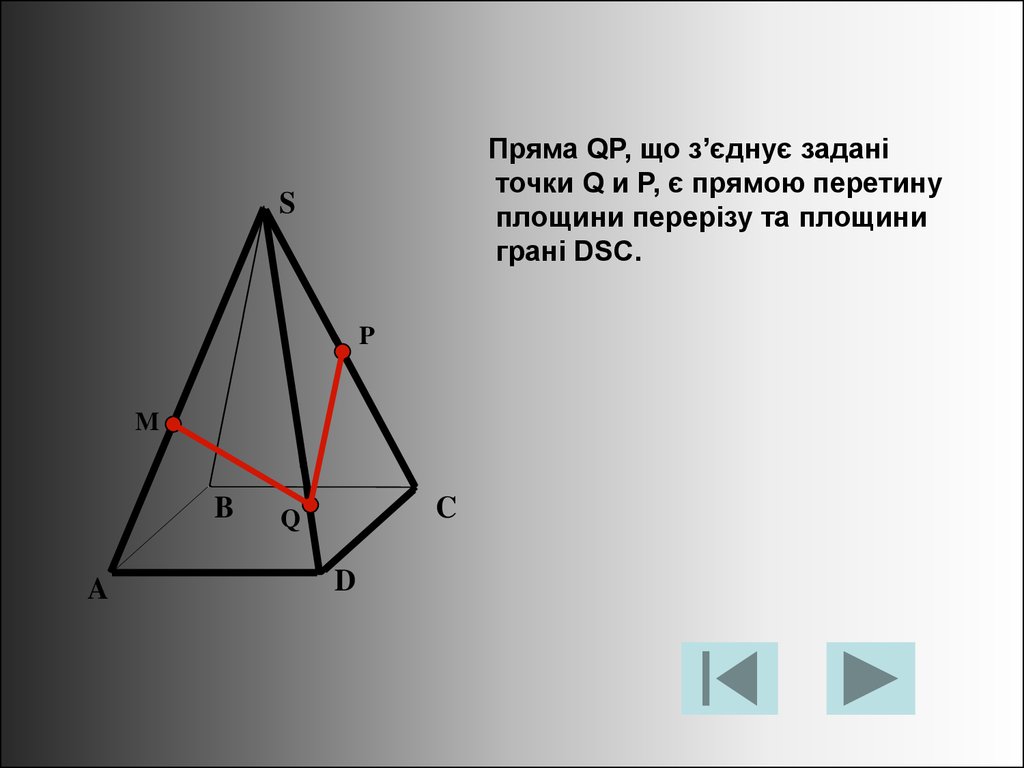
Пряма QP, що з’єднує заданіточки Q и P, є прямою перетину
площини перерізу та площини
грані DSC.
S
P
M
B
A
C
Q
D
20.
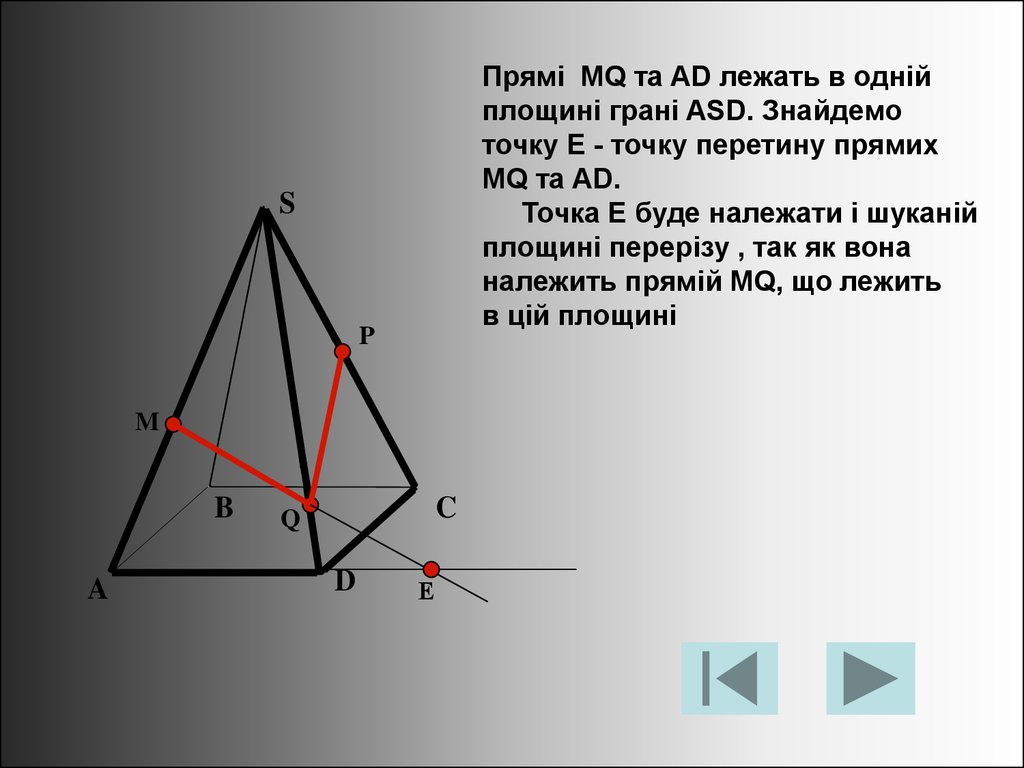
Прямі MQ та AD лежать в однійплощині грані ASD. Знайдемо
точку Е - точку перетину прямих
MQ та AD.
Точка Е буде належати і шуканій
площині перерізу , так як вона
належить прямій MQ, що лежить
в цій площині
S
P
M
B
A
C
Q
D
Е
21.
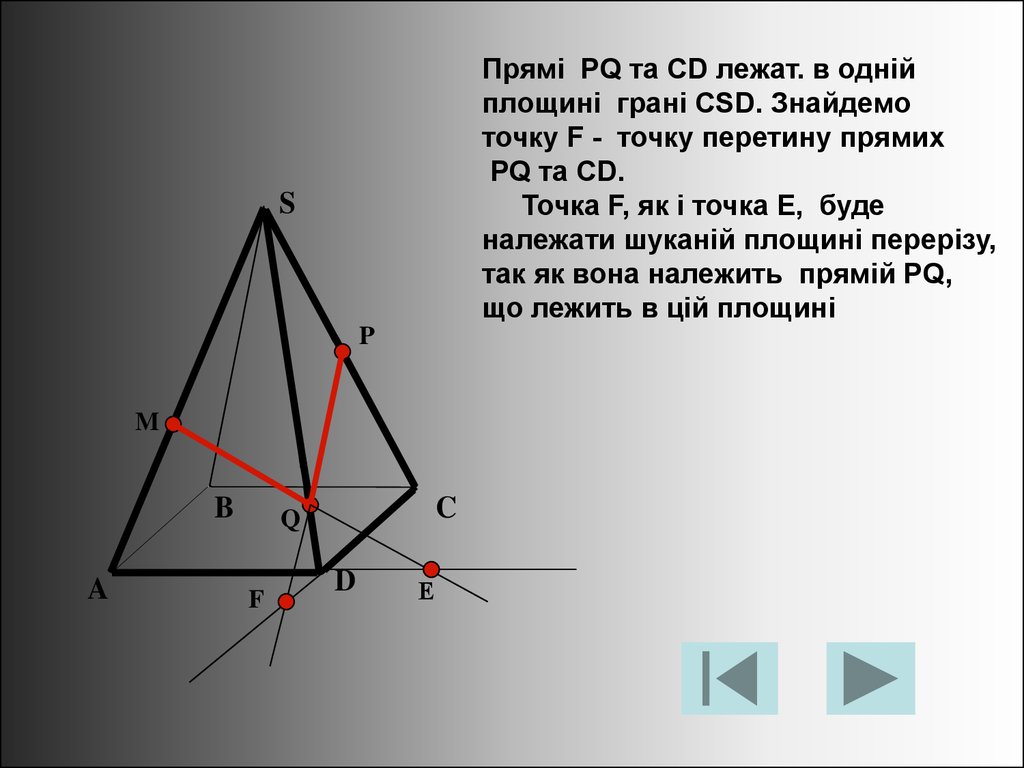
Прямі PQ та CD лежат. в однійплощині грані CSD. Знайдемо
точку F - точку перетину прямих
PQ та CD.
Точка F, як і точка Е, буде
належати шуканій площині перерізу,
так як вона належить прямій PQ,
що лежить в цій площині
S
P
M
B
A
C
Q
F
D
Е
22.
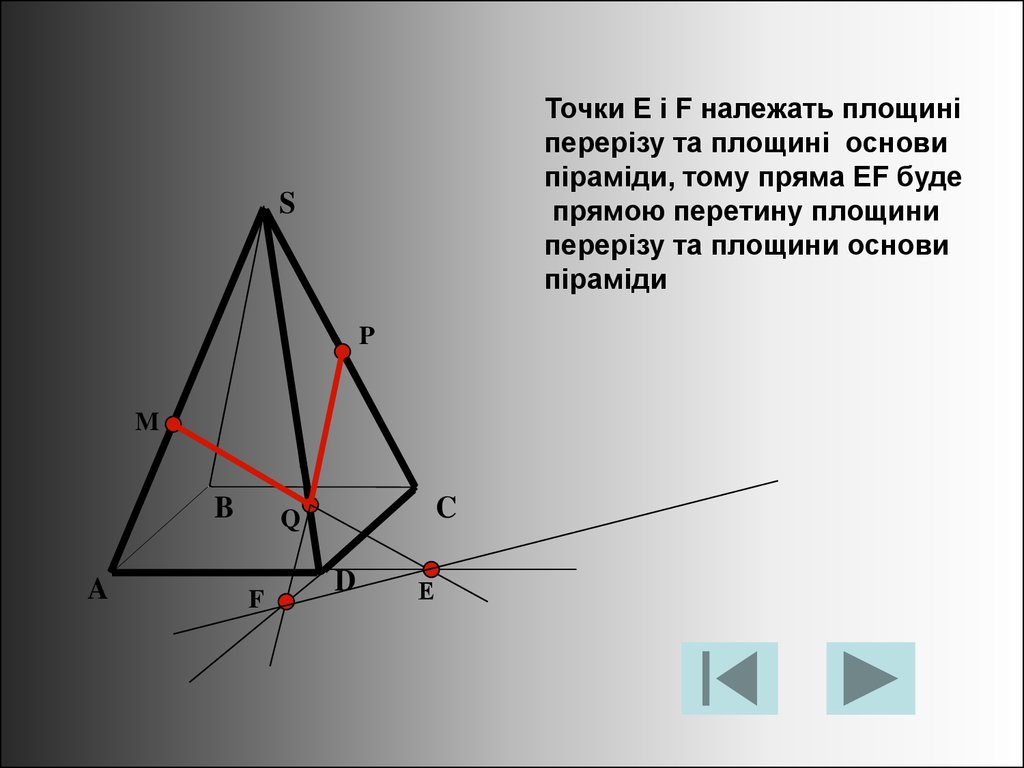
Точки Е і F належать площиніперерізу та площині основи
піраміди, тому пряма EF буде
прямою перетину площини
перерізу та площини основи
піраміди
S
P
M
B
A
C
Q
F
D
Е
23.
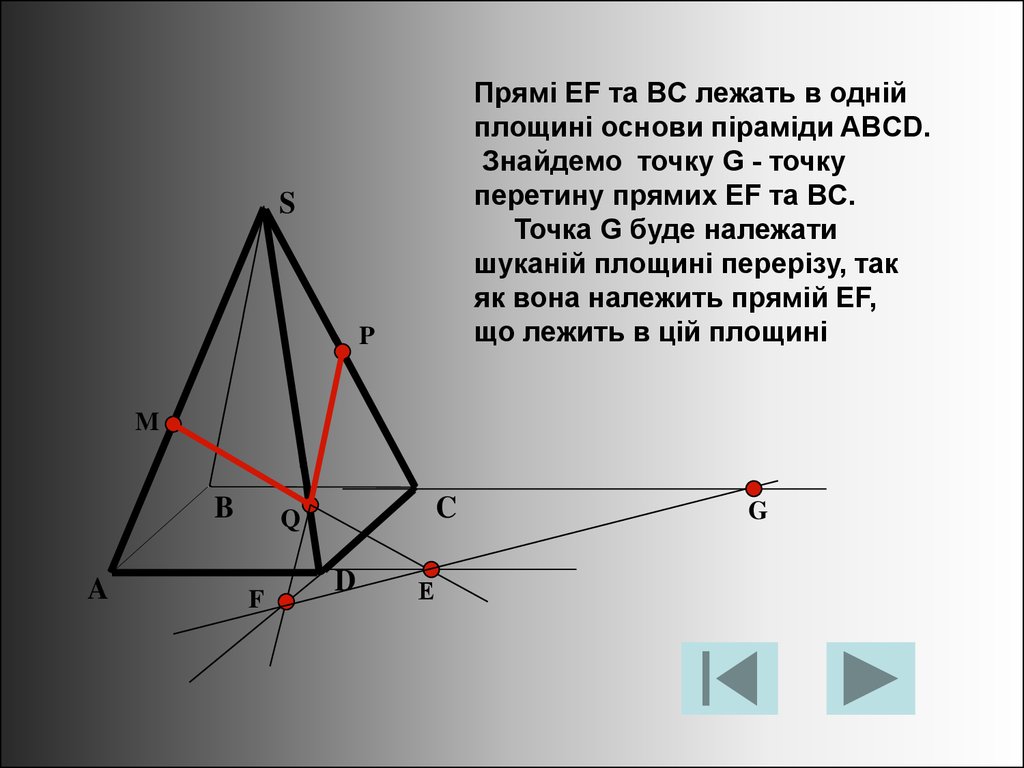
Прямі EF та BC лежать в однійплощині основи піраміди ABCD.
Знайдемо точку G - точку
перетину прямих EF та BC.
Точка G буде належати
шуканій площині перерізу, так
як вона належить прямій EF,
що лежить в цій площині
S
P
M
B
A
C
Q
F
D
Е
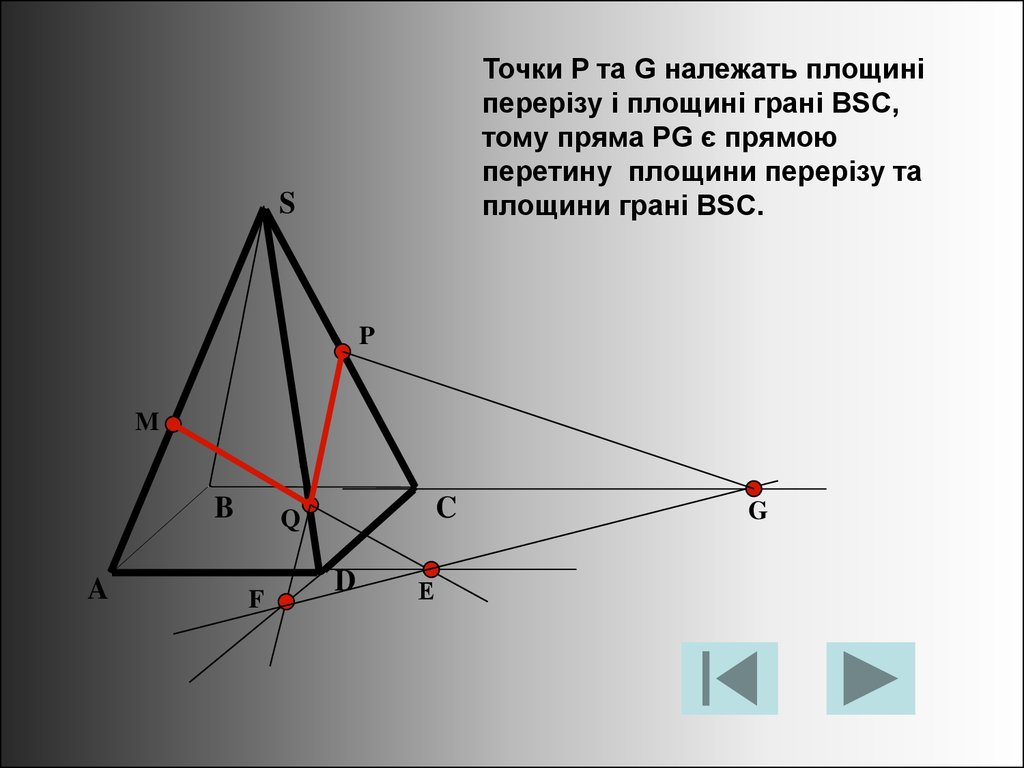
G
24.
Точки P та G належать площиніперерізу і площині грані BSC,
тому пряма PG є прямою
перетину площини перерізу та
площини грані BSC.
S
P
M
B
A
C
Q
F
D
Е
G
25.
Прямою перетину площиниперерізу та площини грані BSC буде
пряма, що є продовженням PG, яка
перетне ребро BS піраміди в точці H.
S
P
H
M
B
A
C
Q
F
D
Е
G
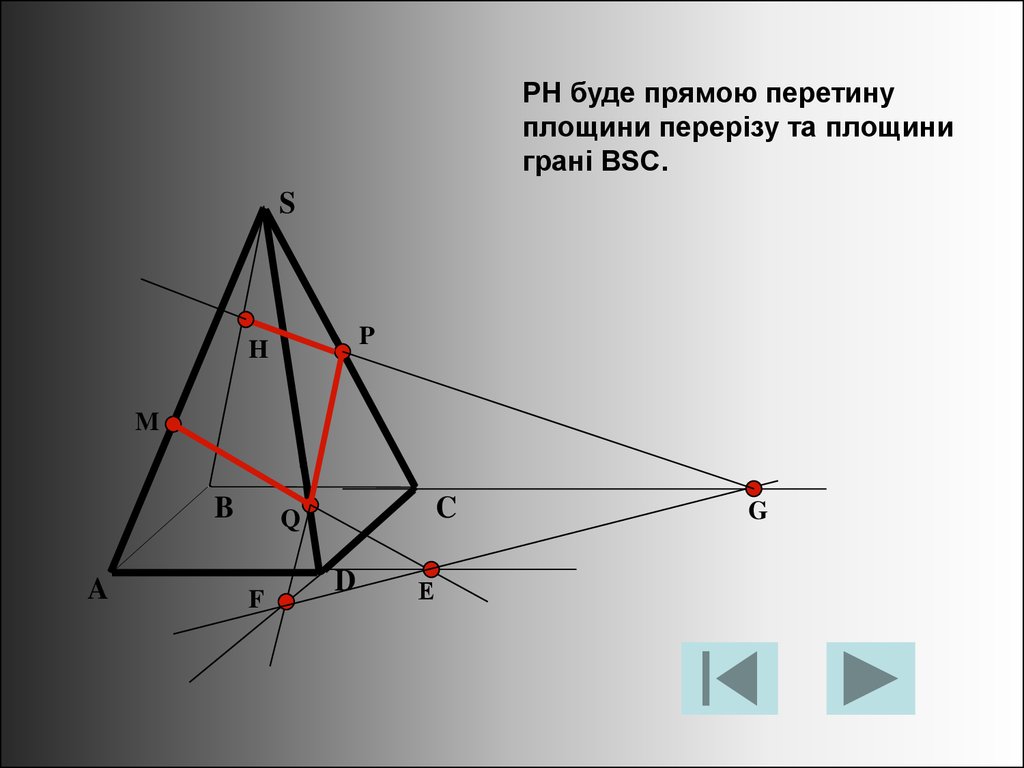
26.
PH буде прямою перетинуплощини перерізу та площини
грані BSC.
S
P
H
M
B
A
C
Q
F
D
Е
G
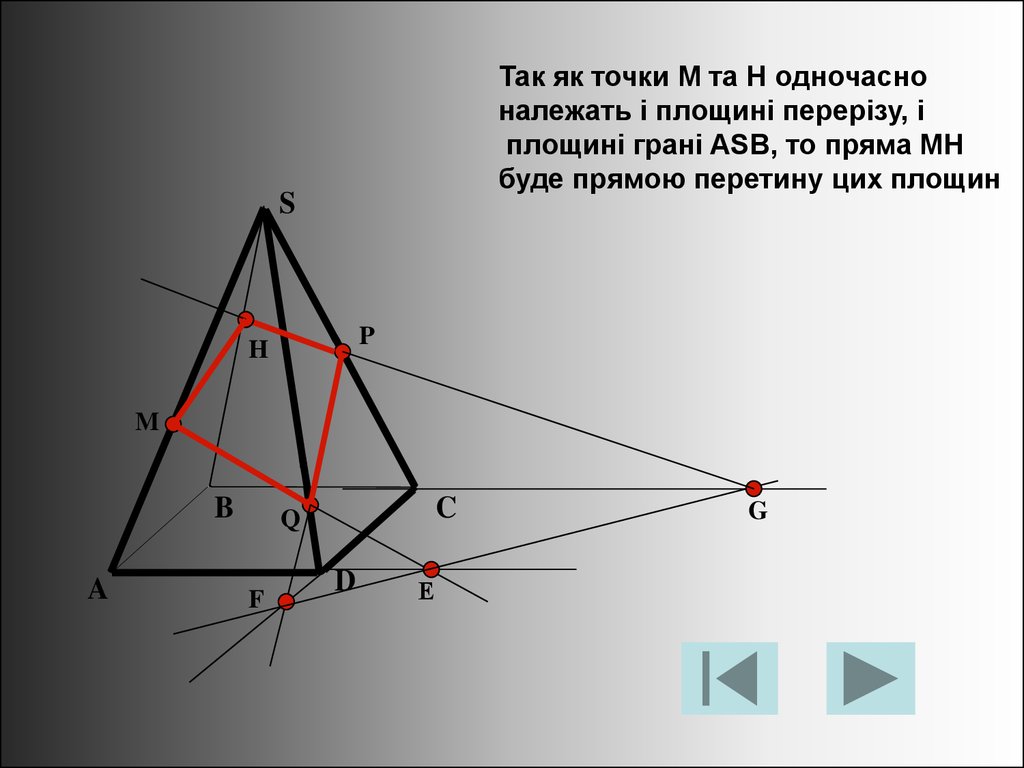
27.
Так як точки M та H одночасноналежать і площині перерізу, і
площині грані ASB, то пряма MH
буде прямою перетину цих площин
S
P
H
M
B
A
C
Q
F
D
Е
G
28.
А чотирикутник MHPQ будешуканим перерізом піраміди
SABCD площиною, що проходить
через задані точки M, P, Q.
H
P
M
B
A
Q
C
D
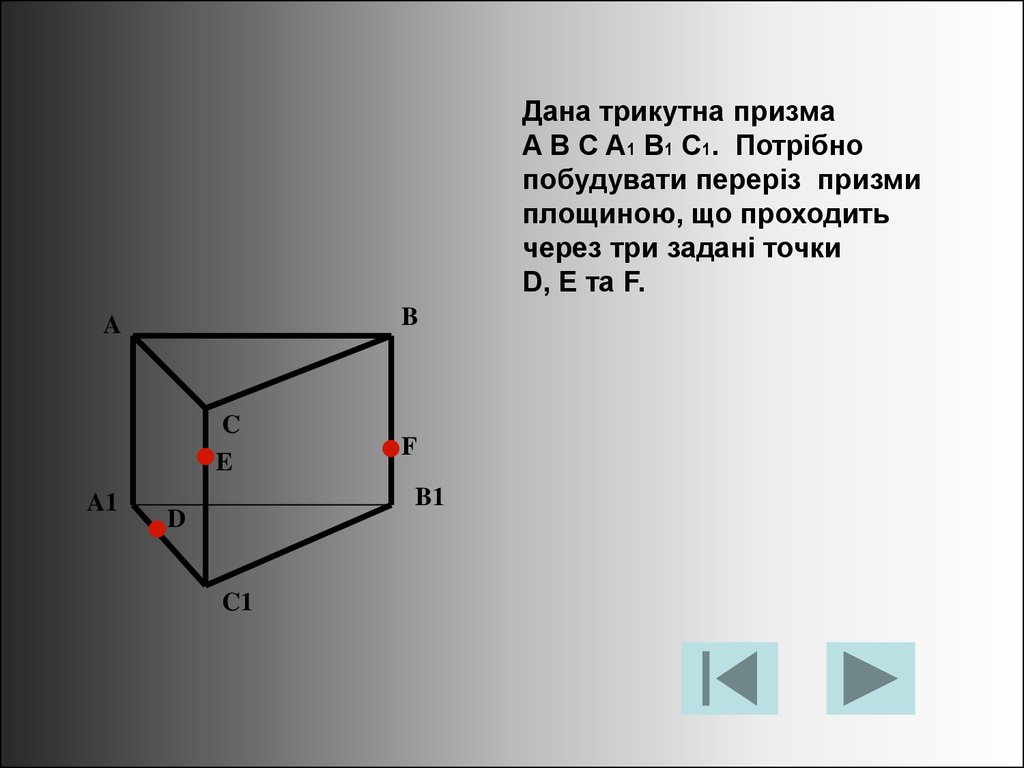
29.
Дана трикутна призмаA B C A1 B1 C1. Потрібно
побудувати переріз призми
площиною, що проходить
через три задані точки
D, E та F.
B
A
C
E
A1
F
B1
D
C1
30.
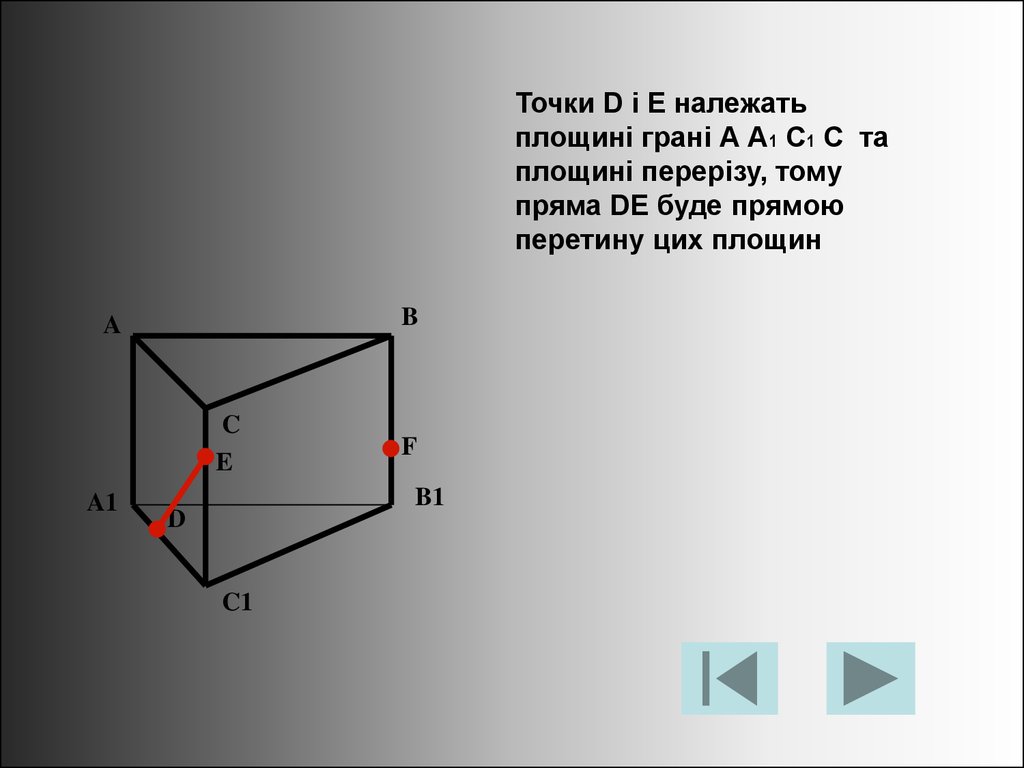
Точки D і E належатьплощині грані А А1 С1 С та
площині перерізу, тому
пряма DE буде прямою
перетину цих площин
B
A
C
E
A1
F
B1
D
C1
31.
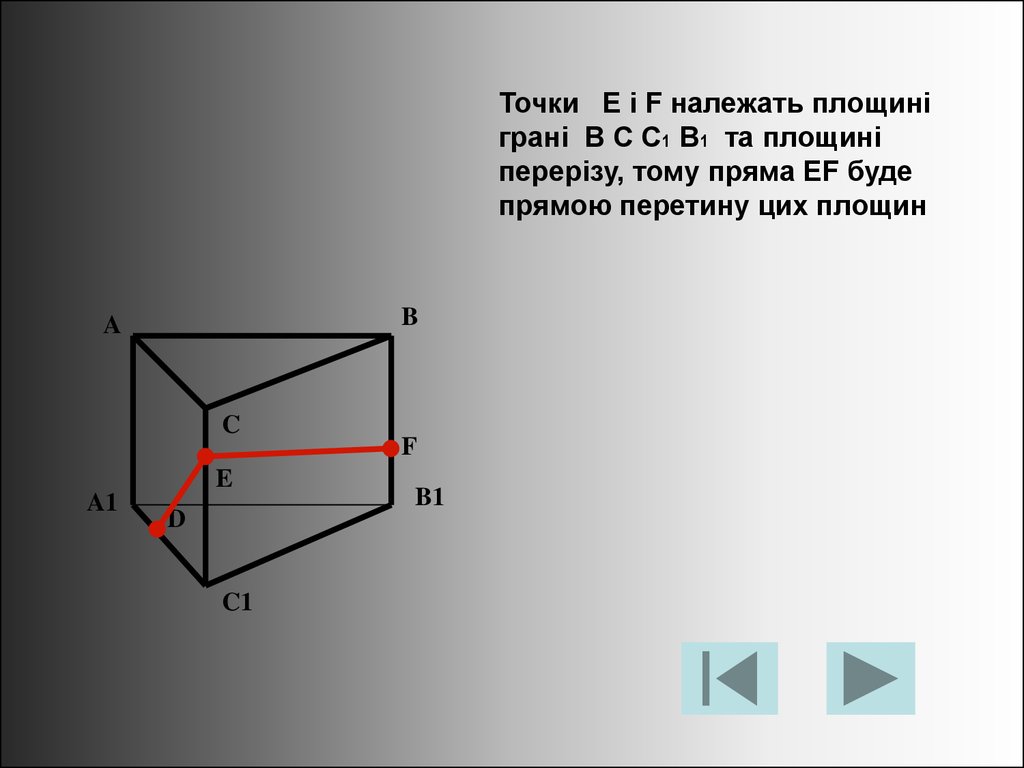
Точки E і F належать площиніграні B C C1 B1 та площині
перерізу, тому пряма EF буде
прямою перетину цих площин
B
A
C
E
A1
D
C1
F
B1
32.
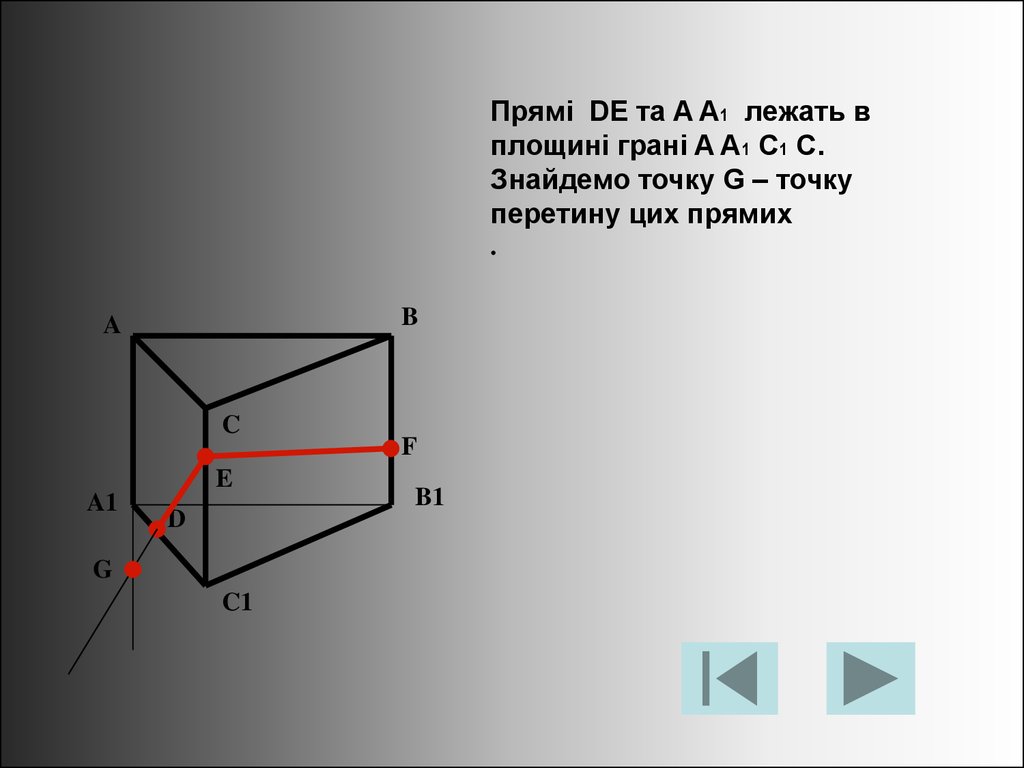
Прямі DE та A A1 лежать вплощині грані A A1 C1 C.
Знайдемо точку G – точку
перетину цих прямих
.
B
A
C
E
A1
D
G
C1
F
B1
33.
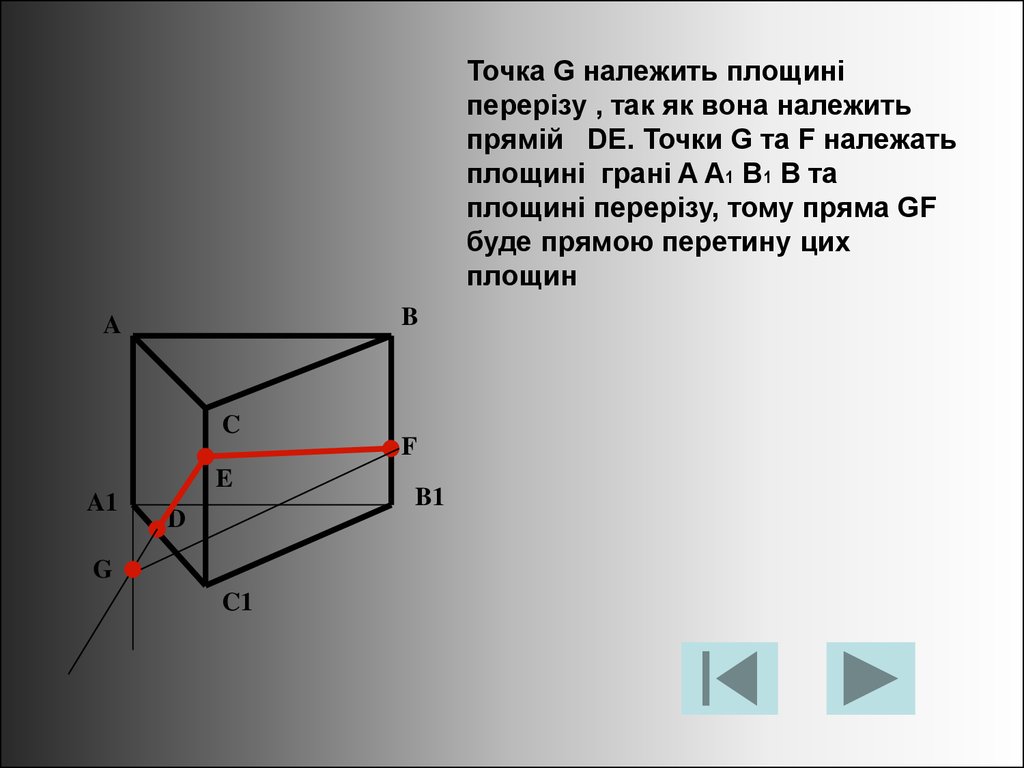
Точка G належить площиніперерізу , так як вона належить
прямій DE. Точки G та F належать
площині грані A A1 B1 B та
площині перерізу, тому пряма GF
буде прямою перетину цих
площин
B
A
C
E
A1
D
G
C1
F
B1
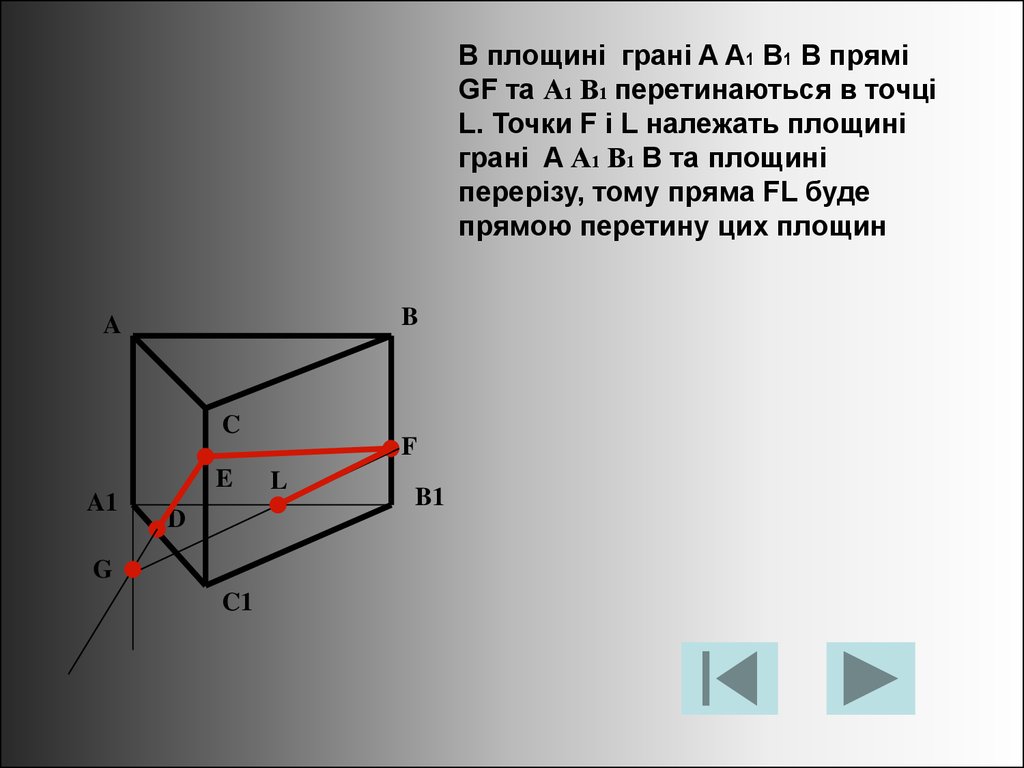
34.
В площині грані A A1 B1 B пряміGF та A1 B1 перетинаються в точці
L. Точки F і L належать площині
грані A A1 B1 B та площині
перерізу, тому пряма FL буде
прямою перетину цих площин
B
A
C
E
A1
D
G
C1
F
L
B1
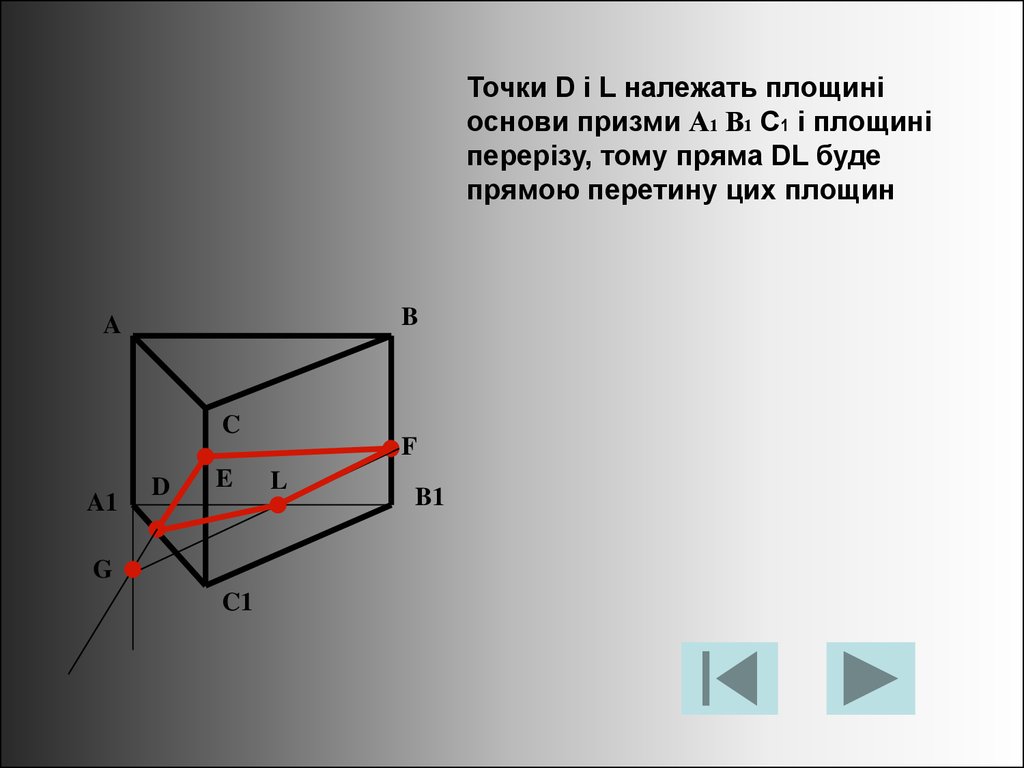
35.
Точки D і L належать площиніоснови призми A1 B1 C1 і площині
перерізу, тому пряма DL буде
прямою перетину цих площин
B
A
C
A1
D
E
G
C1
F
L
B1
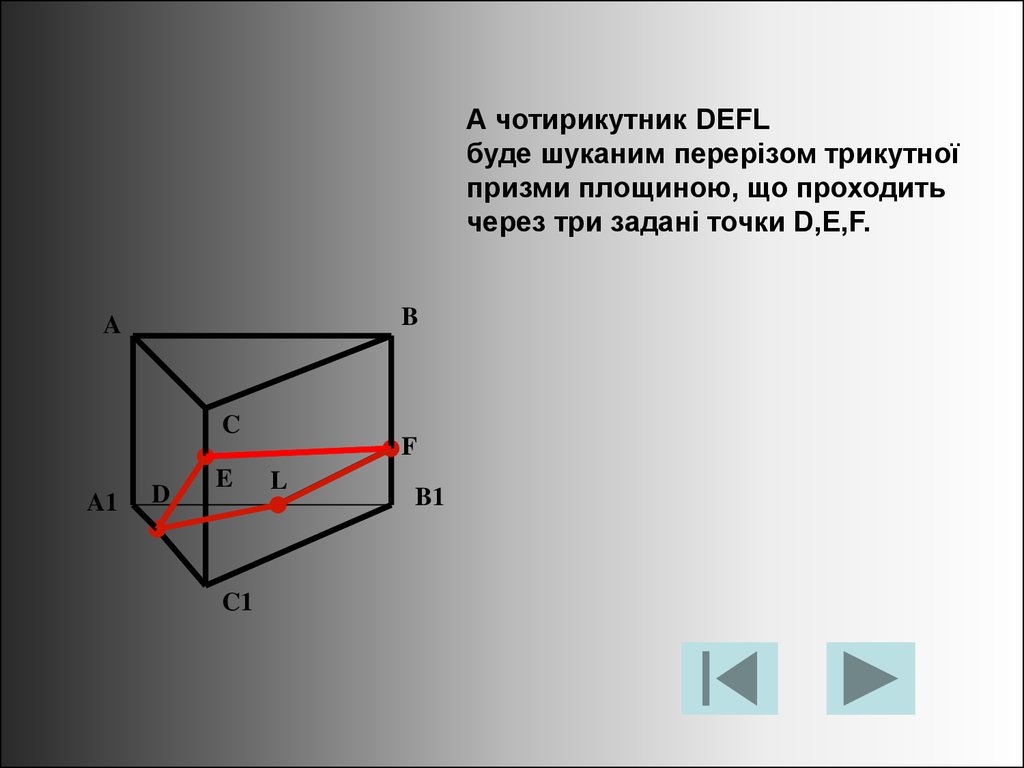
36.
А чотирикутник DEFLбуде шуканим перерізом трикутної
призми площиною, що проходить
через три задані точки D,E,F.
B
A
C
A1
D
E
C1
F
L
B1





 Математика
Математика








