Похожие презентации:
Піраміда. Її основні елементи. Види пірамід
1.
2.
Тема:Піраміда. Її основні елементи.
Види пірамід.
3.
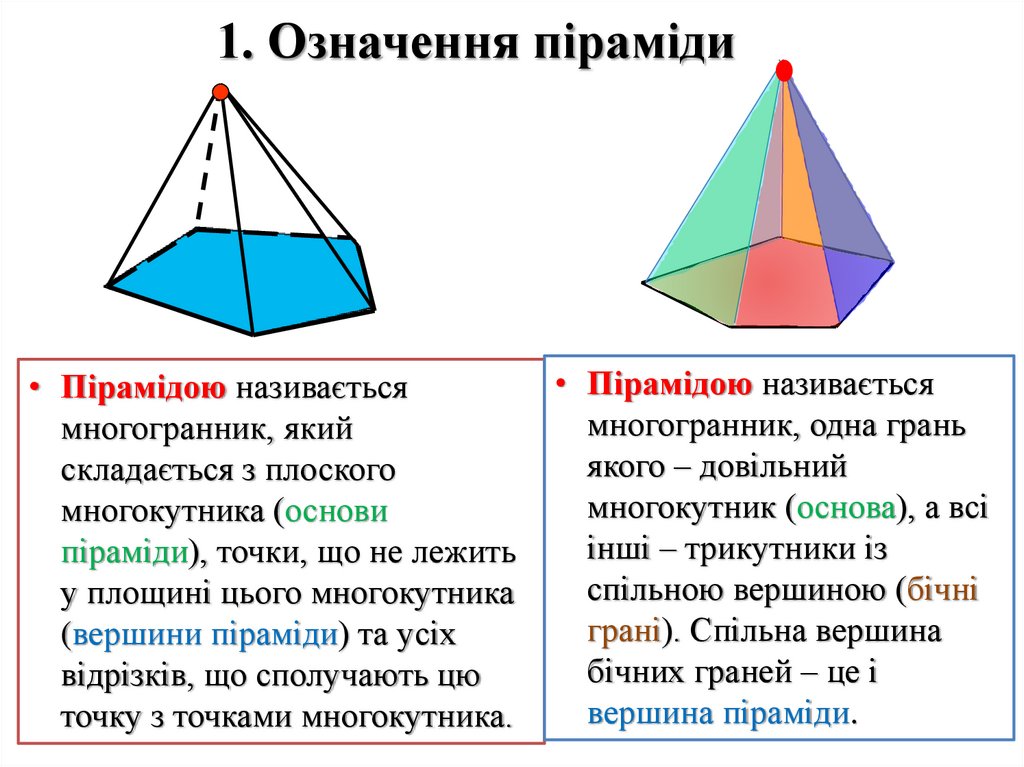
1. Означення піраміди• Пірамідою називається
многогранник, який
складається з плоского
многокутника (основи
піраміди), точки, що не лежить
у площині цього многокутника
(вершини піраміди) та усіх
відрізків, що сполучають цю
точку з точками многокутника.
• Пірамідою називається
многогранник, одна грань
якого – довільний
многокутник (основа), а всі
інші – трикутники із
спільною вершиною (бічні
грані). Спільна вершина
бічних граней – це і
вершина піраміди.
4.
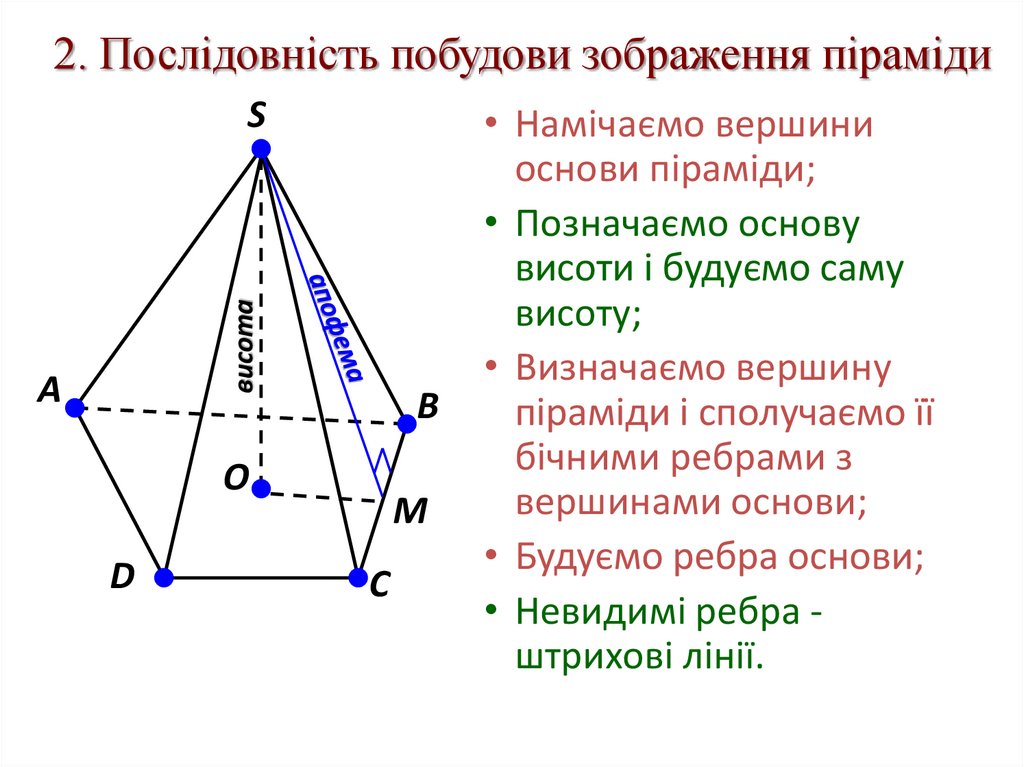
2. Послідовність побудови зображення пірамідивисота
S
А
В
O
D
M
С
• Намічаємо вершини
основи піраміди;
• Позначаємо основу
висоти і будуємо саму
висоту;
• Визначаємо вершину
піраміди і сполучаємо її
бічними ребрами з
вершинами основи;
• Будуємо ребра основи;
• Невидимі ребра штрихові лінії.
5.
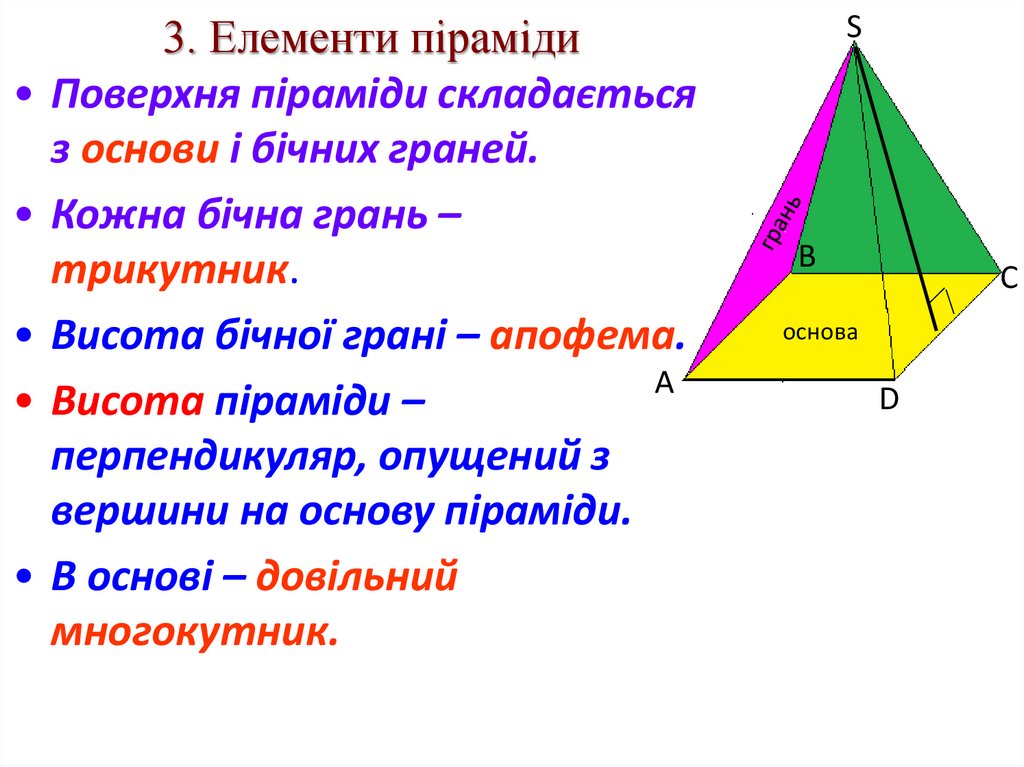
3. Елементи піраміди• Поверхня піраміди складається
з основи і бічних граней.
• Кожна бічна грань –
трикутник.
• Висота бічної грані – апофема.
A
• Висота піраміди –
перпендикуляр, опущений з
вершини на основу піраміди.
• В основі – довільний
многокутник.
S
B
C
основа
D
6.
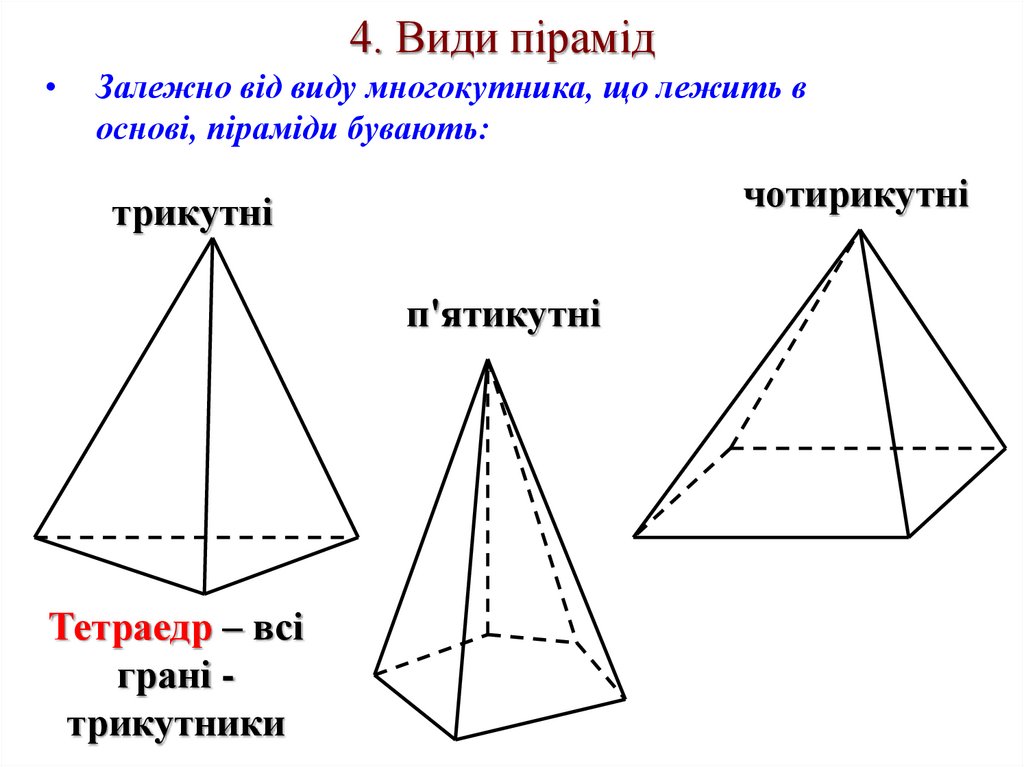
4. Види пірамідЗалежно від виду многокутника, що лежить в
основі, піраміди бувають:
чотирикутні
трикутні
п'ятикутні
Тетраедр – всі
грані трикутники
7.
ПірамідиПравильні
Неправильні
• Правильною називається піраміда,
в основі якої лежить правильний
многокутник,
а її вершина проектується в центр цього
многокутника.
( центр вписаного і описаного кола)
8.
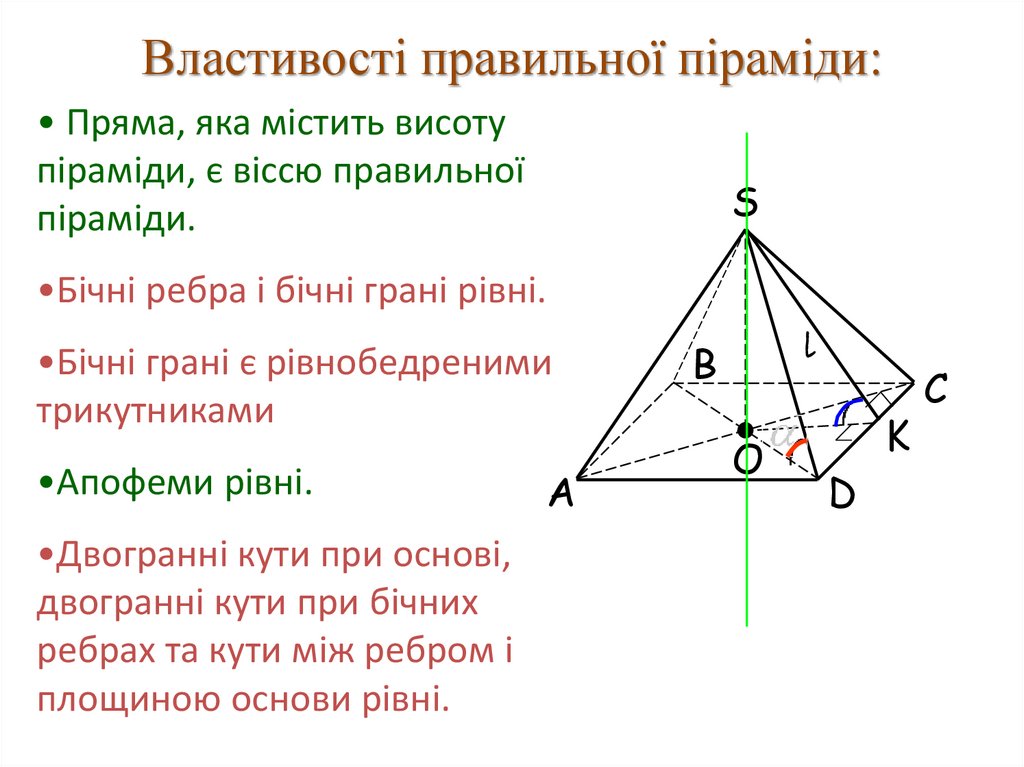
Властивості правильної піраміди:• Пряма, яка містить висоту
піраміди, є віссю правильної
піраміди.
S
•Бічні ребра і бічні грані рівні.
•Бічні грані є рівнобедреними
трикутниками
•Апофеми рівні.
•Двогранні кути при основі,
двогранні кути при бічних
ребрах та кути між ребром і
площиною основи рівні.
А
l
В
O
K
D
С
9.
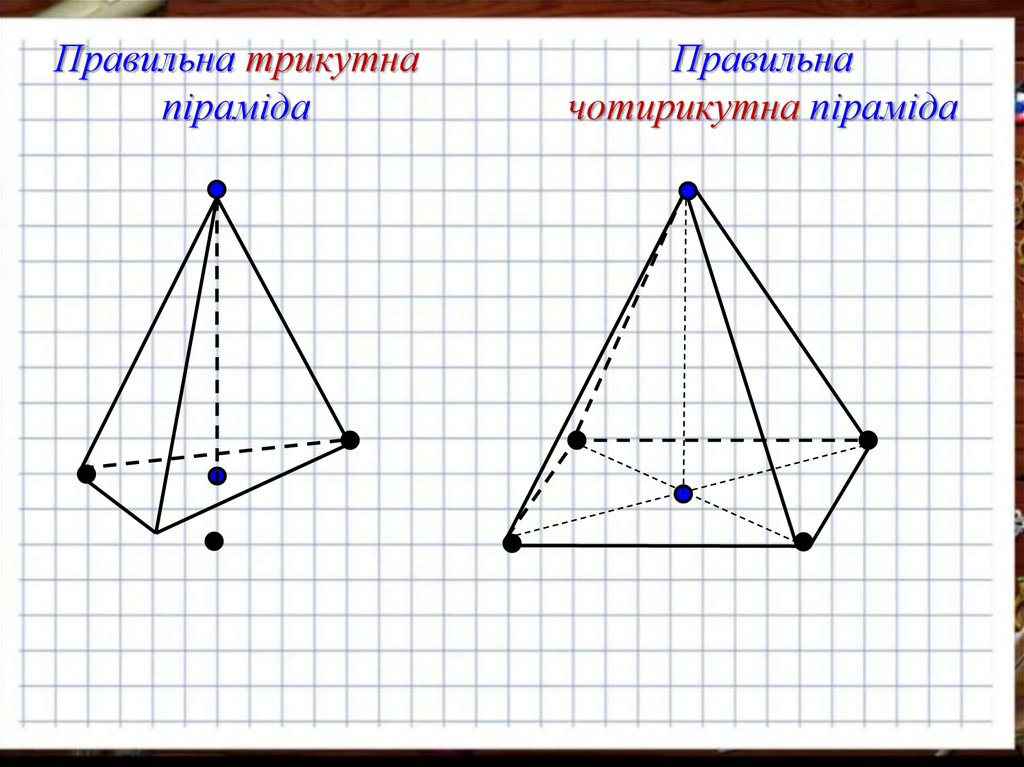
Правильна трикутнапіраміда
Правильна
чотирикутна піраміда
10.
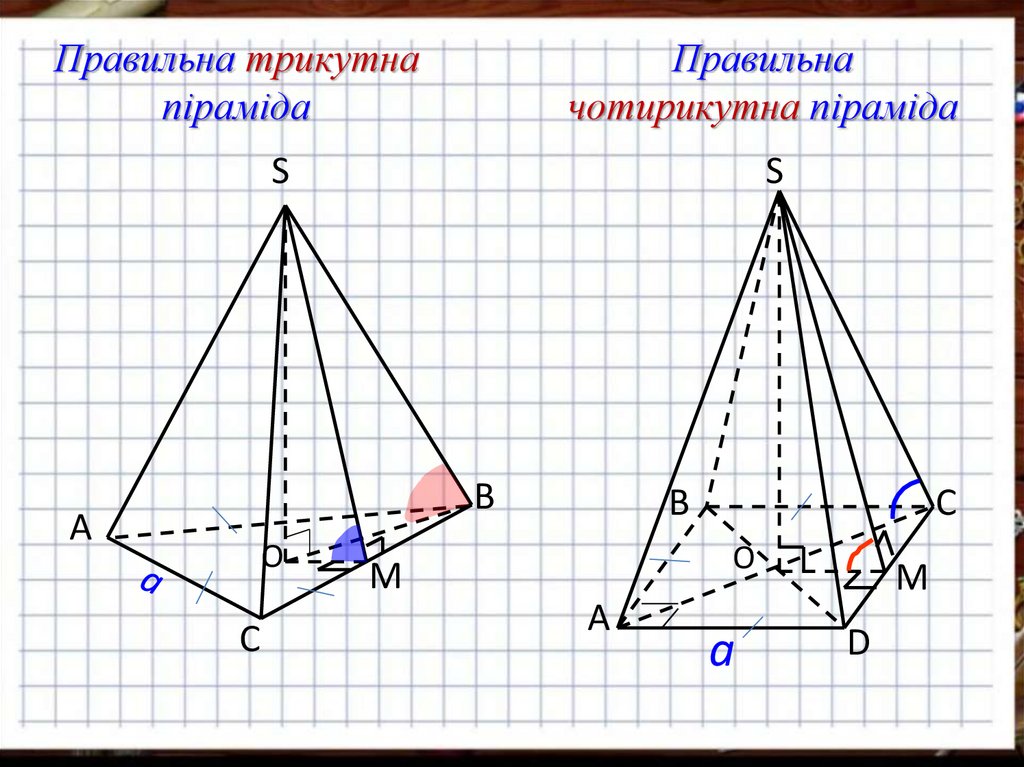
Правильна трикутнапіраміда
Правильна
чотирикутна піраміда
S
S
В
А
О
С
B
C
O
M
A
a
M
D
11.
ra
2 3
a
R
3
a
r
2
d a 2
R
2
2
12.
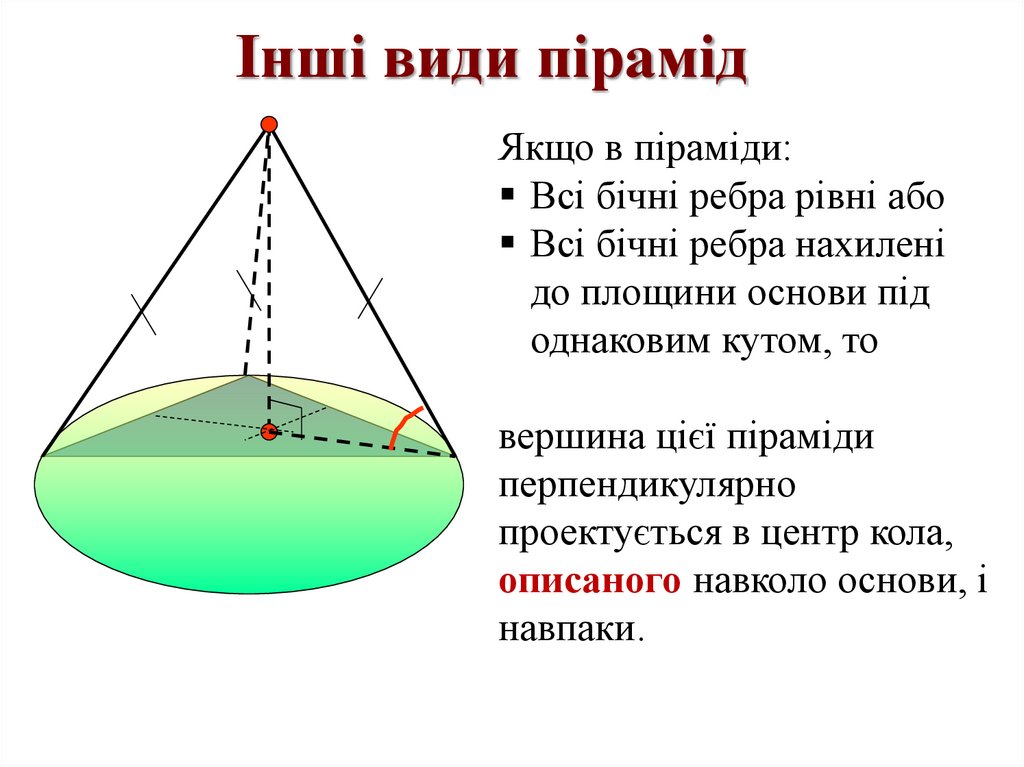
Інші види пірамідЯкщо в піраміди:
Всі бічні ребра рівні або
Всі бічні ребра нахилені
до площини основи під
однаковим кутом, то
вершина цієї піраміди
перпендикулярно
проектується в центр кола,
описаного навколо основи, і
навпаки.
13.
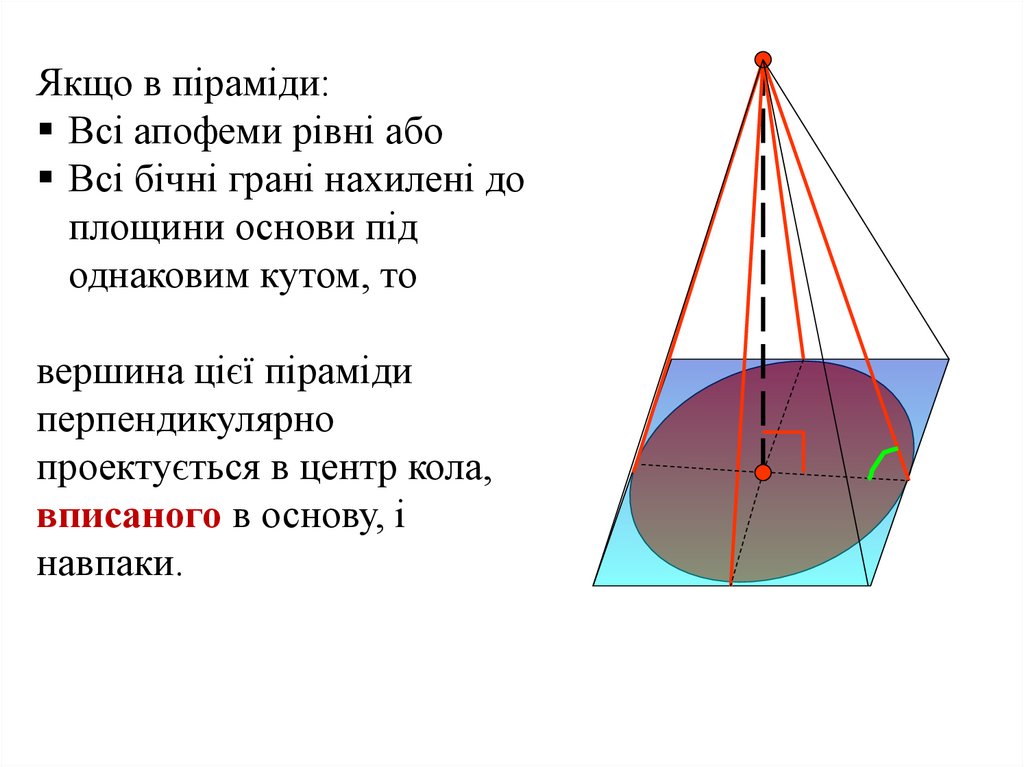
Якщо в піраміди:Всі апофеми рівні або
Всі бічні грані нахилені до
площини основи під
однаковим кутом, то
вершина цієї піраміди
перпендикулярно
проектується в центр кола,
вписаного в основу, і
навпаки.
14.
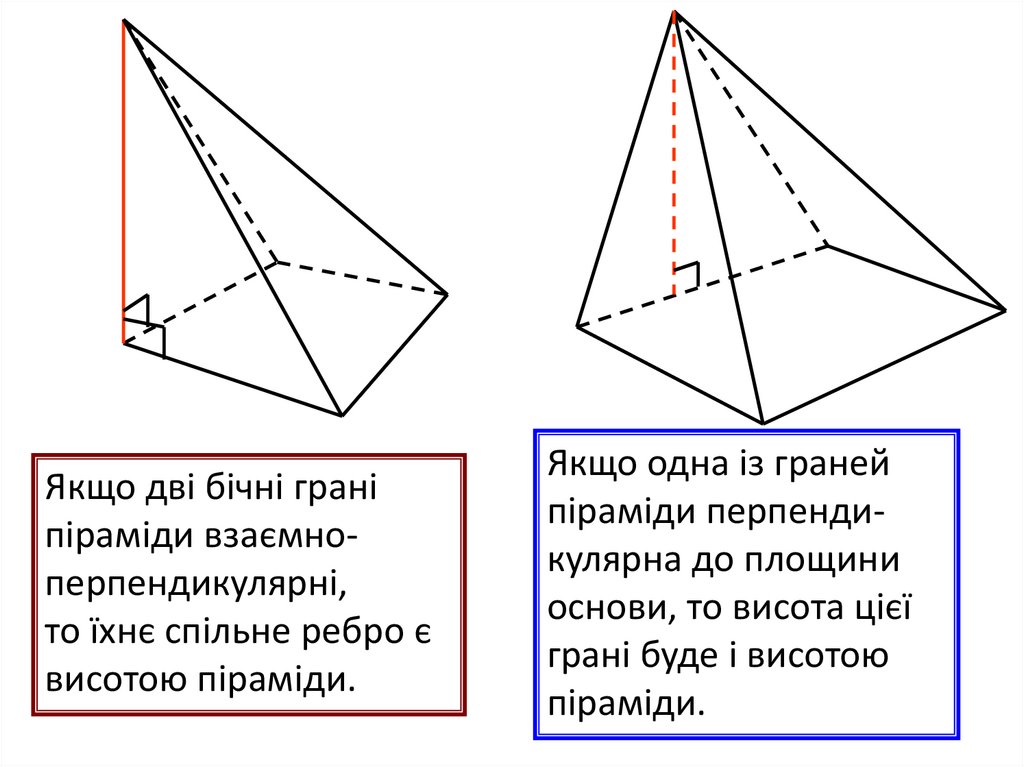
Якщо дві бічні граніпіраміди взаємноперпендикулярні,
то їхнє спільне ребро є
висотою піраміди.
Якщо одна із граней
піраміди перпендикулярна до площини
основи, то висота цієї
грані буде і висотою
піраміди.
15.
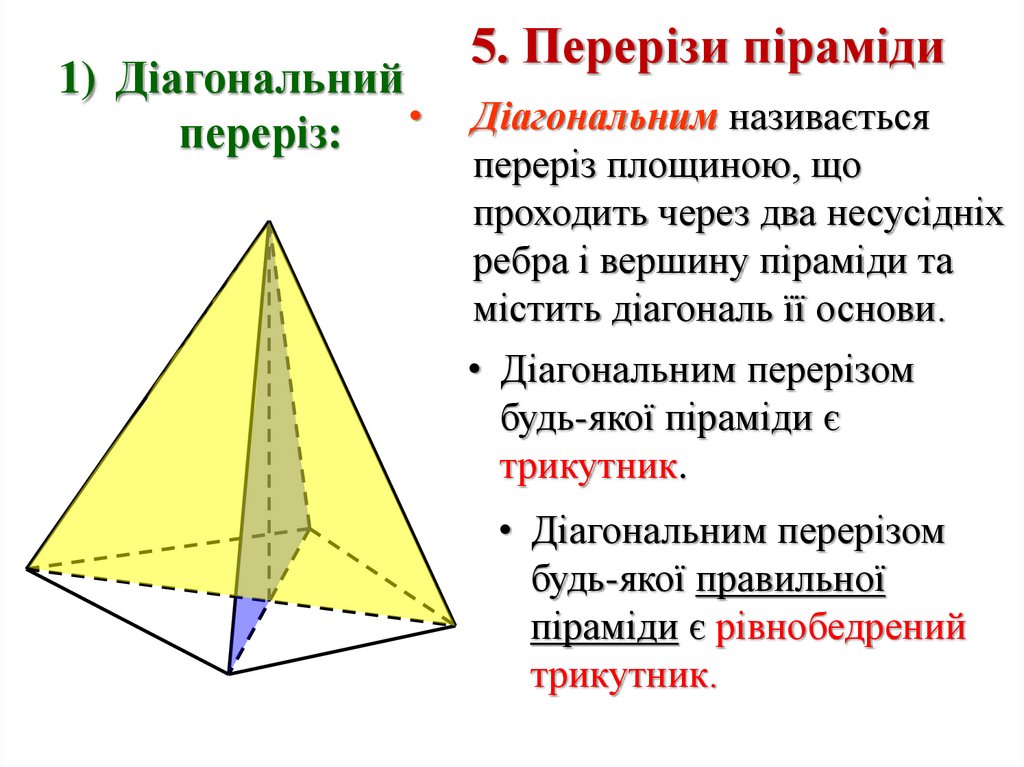
1) Діагональнийпереріз:
5. Перерізи піраміди
Діагональним називається
переріз площиною, що
проходить через два несусідніх
ребра і вершину піраміди та
містить діагональ її основи.
• Діагональним перерізом
будь-якої піраміди є
трикутник.
• Діагональним перерізом
будь-якої правильної
піраміди є рівнобедрений
трикутник.
16.
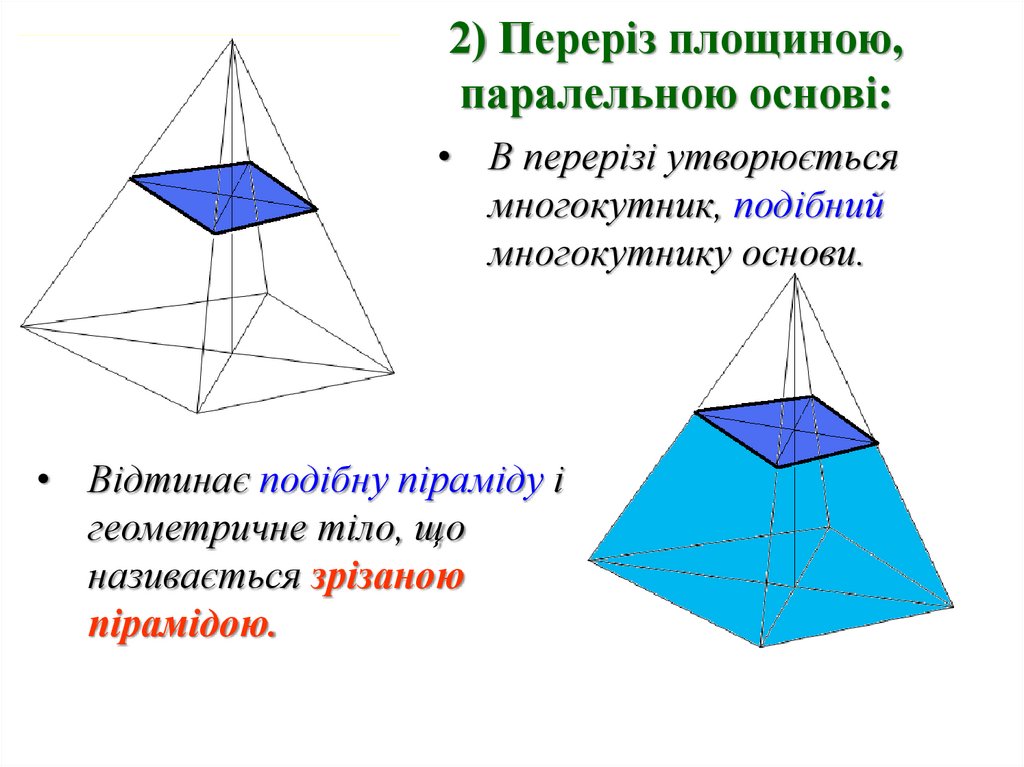
2) Переріз площиною,паралельною основі:
• В перерізі утворюється
многокутник, подібний
многокутнику основи.
• Відтинає подібну піраміду і
геометричне тіло, що
називається зрізаною
пірамідою.
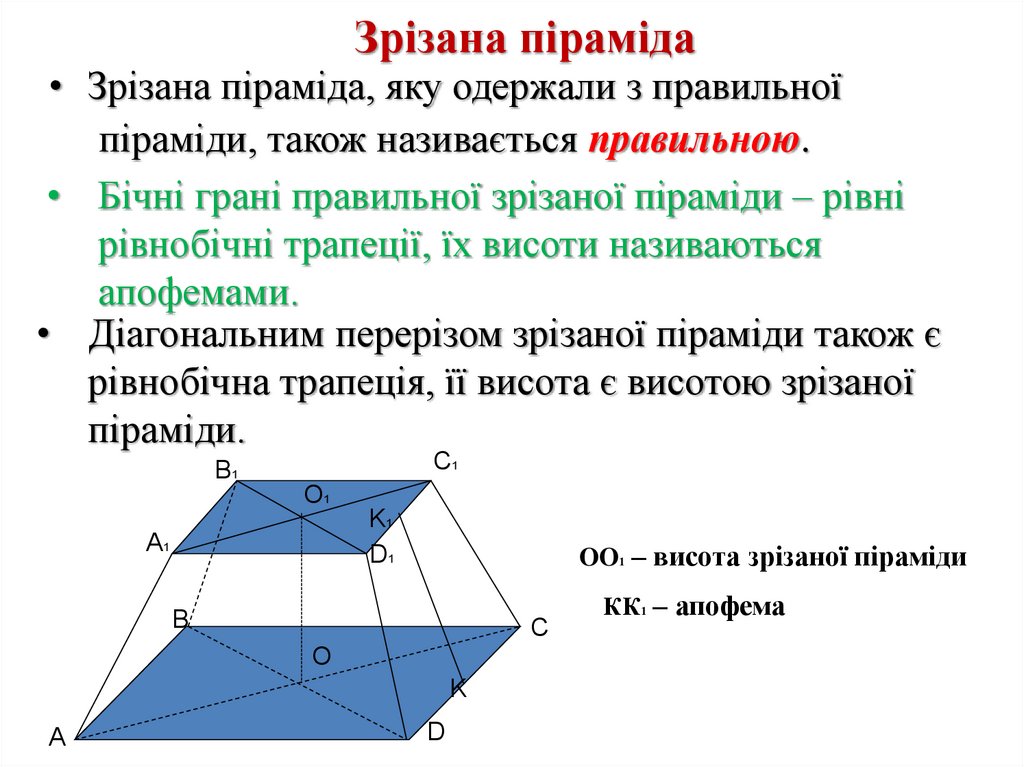
17. Зрізана піраміда
• Зрізана піраміда, яку одержали з правильноїпіраміди, також називається правильною.
• Бічні грані правильної зрізаної піраміди – рівні
рівнобічні трапеції, їх висоти називаються
апофемами.
• Діагональним перерізом зрізаної піраміди також є
рівнобічна трапеція, її висота є висотою зрізаної
піраміди.
C1
B1
O1
K1
D1
A1
OO1 – висота зрізаної піраміди
B
C
O
K
A
D
КК1 – апофема
18.
Розв'язування задач назнаходження елементів піраміди
19.
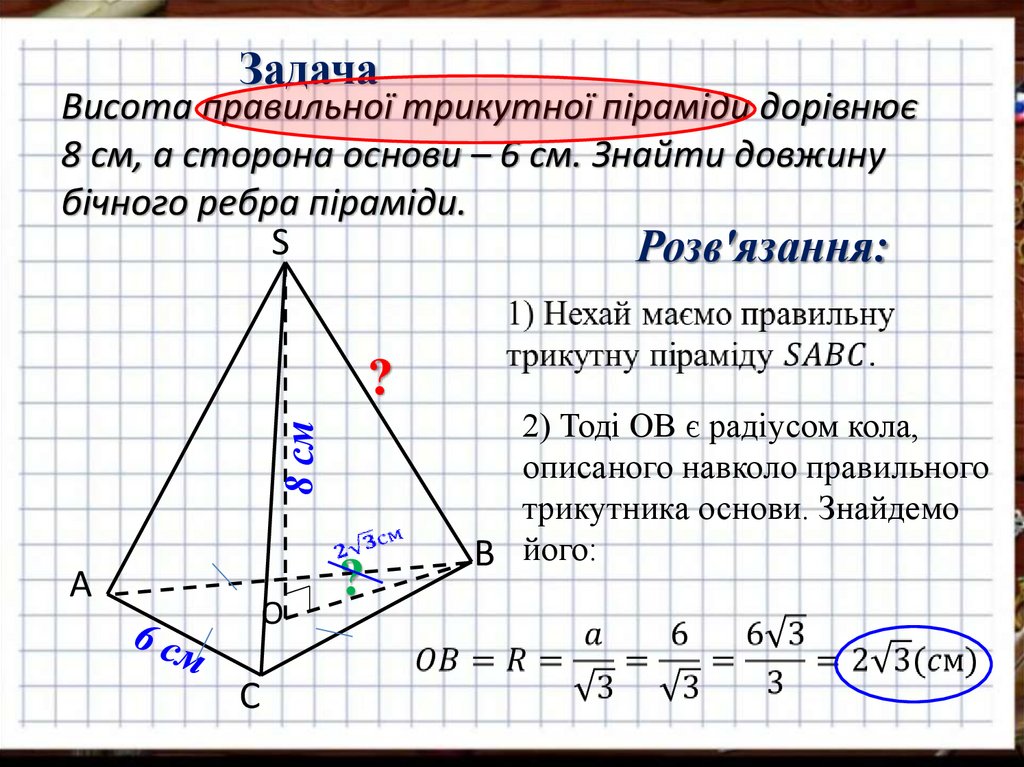
ЗадачаВисота правильної трикутної піраміди дорівнює
8 см, а сторона основи – 6 см. Знайти довжину
бічного ребра піраміди.
S
Розв'язання:
8 см
?
А
О
С
?
2) Тоді ОВ є радіусом кола,
описаного навколо правильного
трикутника основи. Знайдемо
В його:
20.
21.
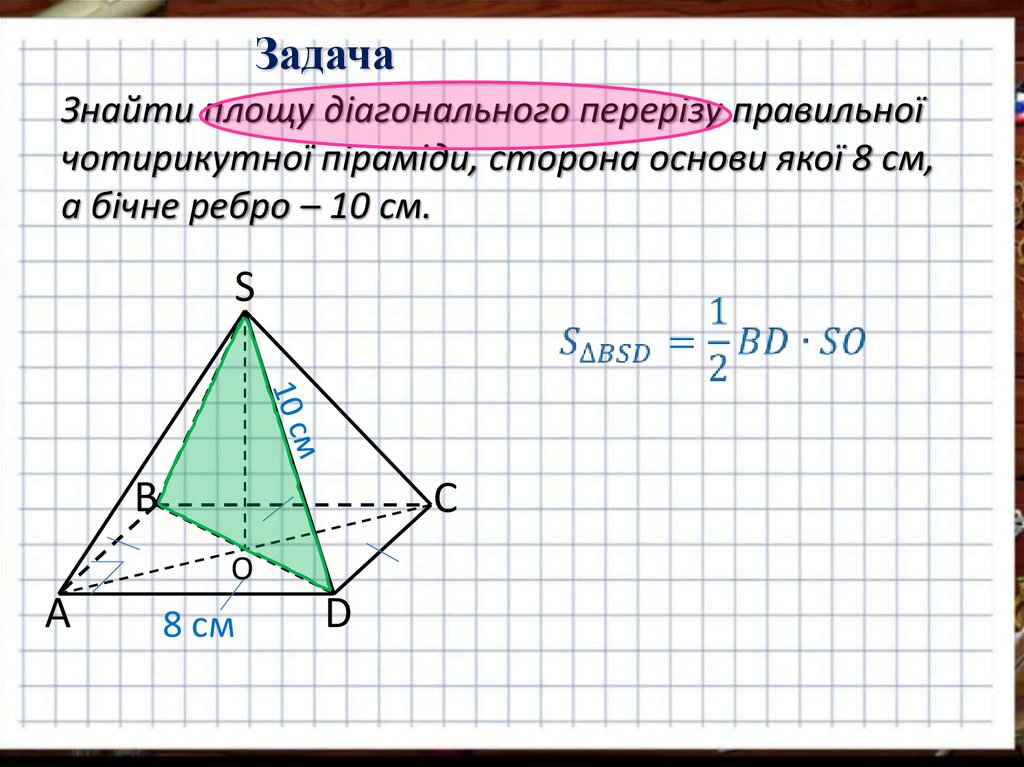
ЗадачаЗнайти площу діагонального перерізу правильної
чотирикутної піраміди, сторона основи якої 8 см,
а бічне ребро – 10 см.
S
B
C
O
A
8 см
D
22.
ЗадачаРозв'язання:
6 см
S
A
?
B
O
C
М
4)


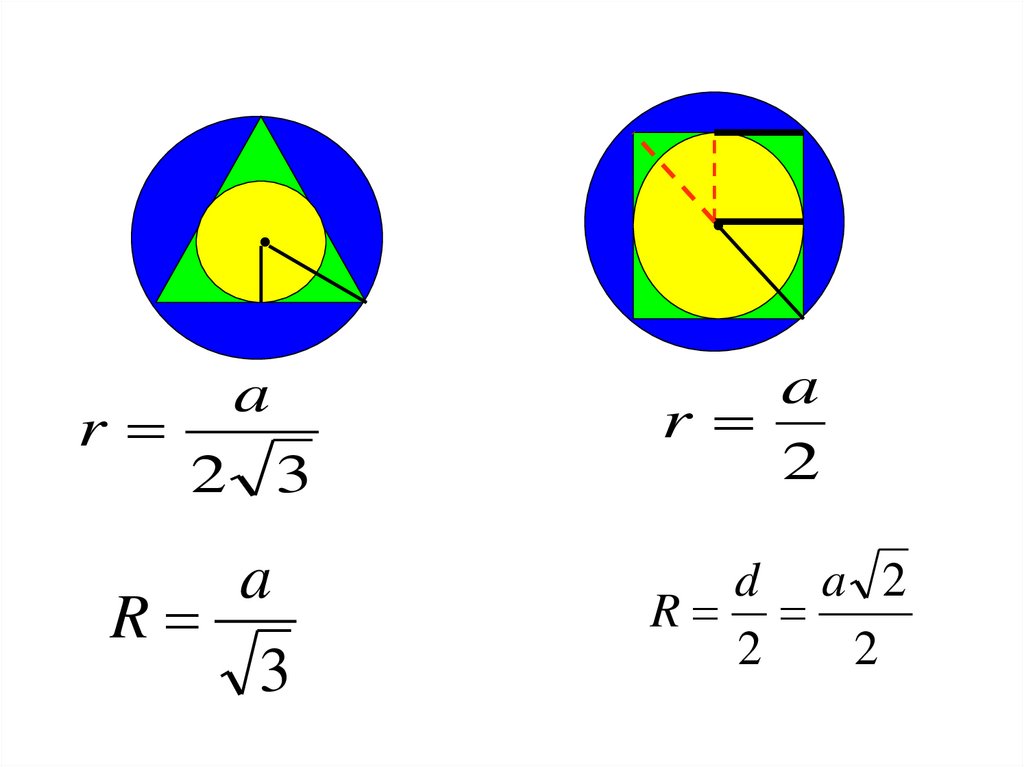


 Математика
Математика








