Многогранник та його елементи. Правильні многогранники. Призма, види призм. Площа та об’єм призми

1.

Многогранник та його
елементи. Правильні
многогранники. Призма, види
призм. Площа та об’єм призми.

2.

2

3.

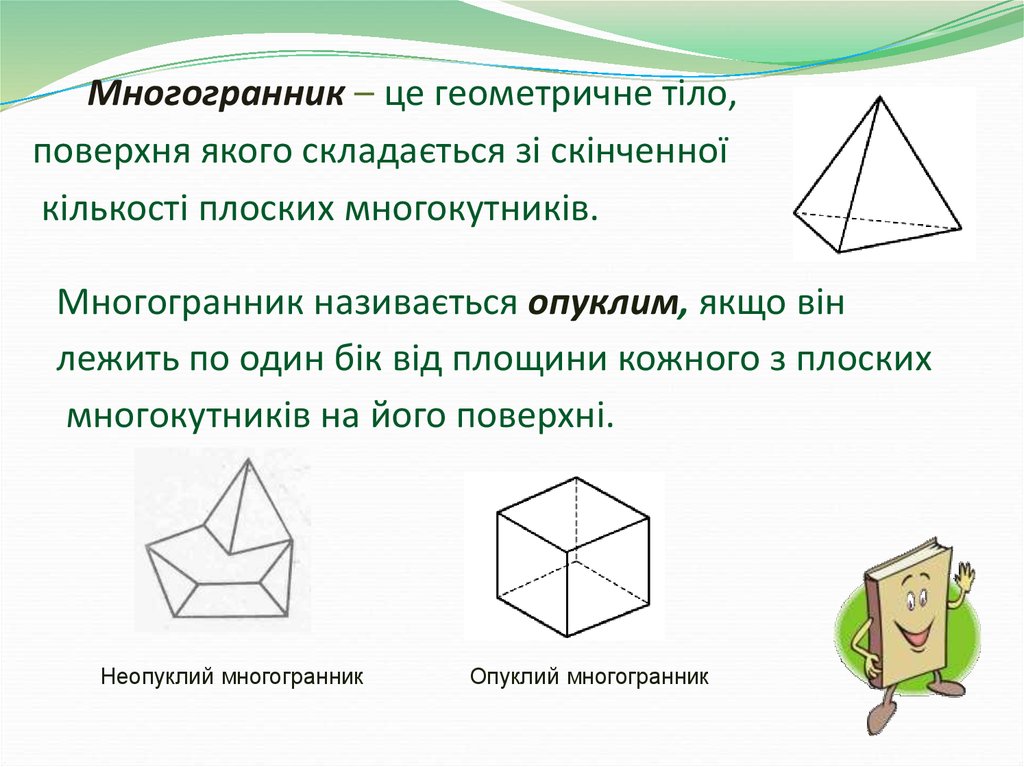
Многогранник – це геометричне тіло,
поверхня якого складається зі скінченної
кількості плоских многокутників.
Многогранник називається опуклим, якщо він
лежить по один бік від площини кожного з плоских
многокутників на його поверхні.
Неопуклий многогранник
Опуклий многогранник

4.

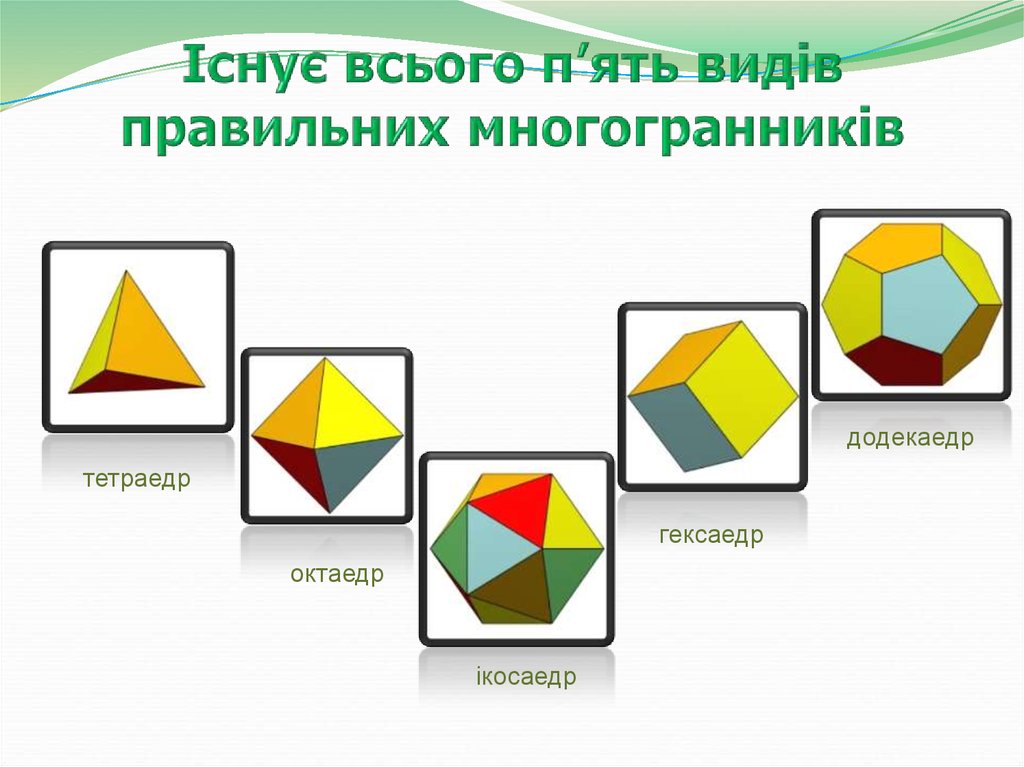
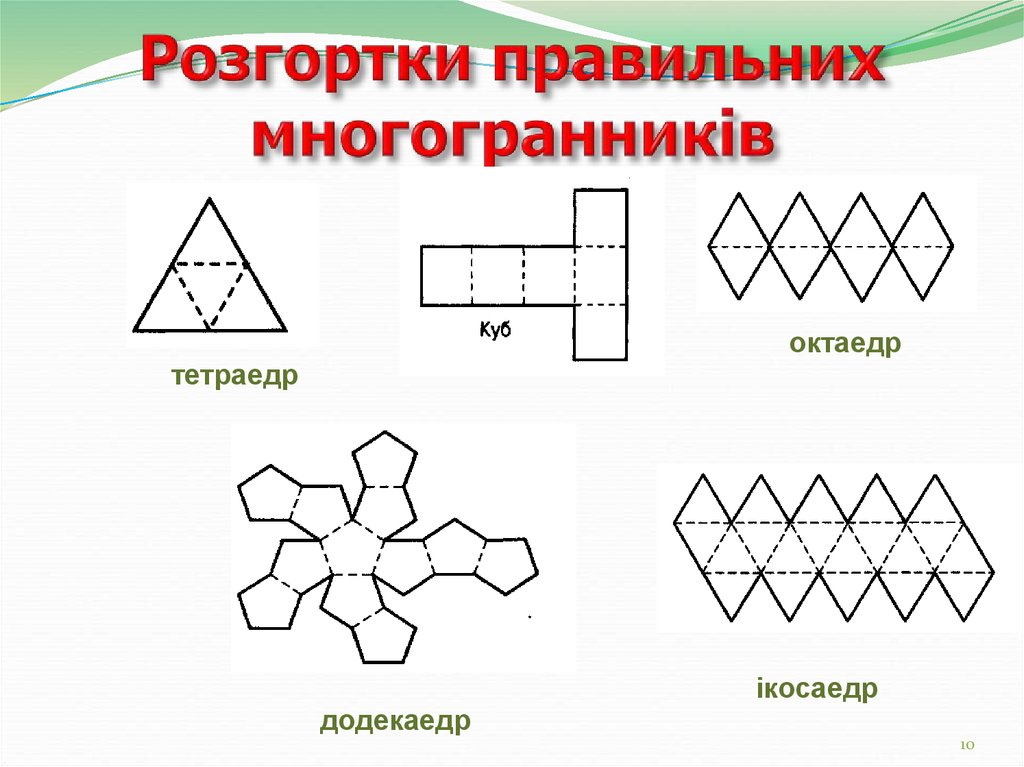
додекаедр
тетраедр
гексаедр
октаедр
ікосаедр

5.

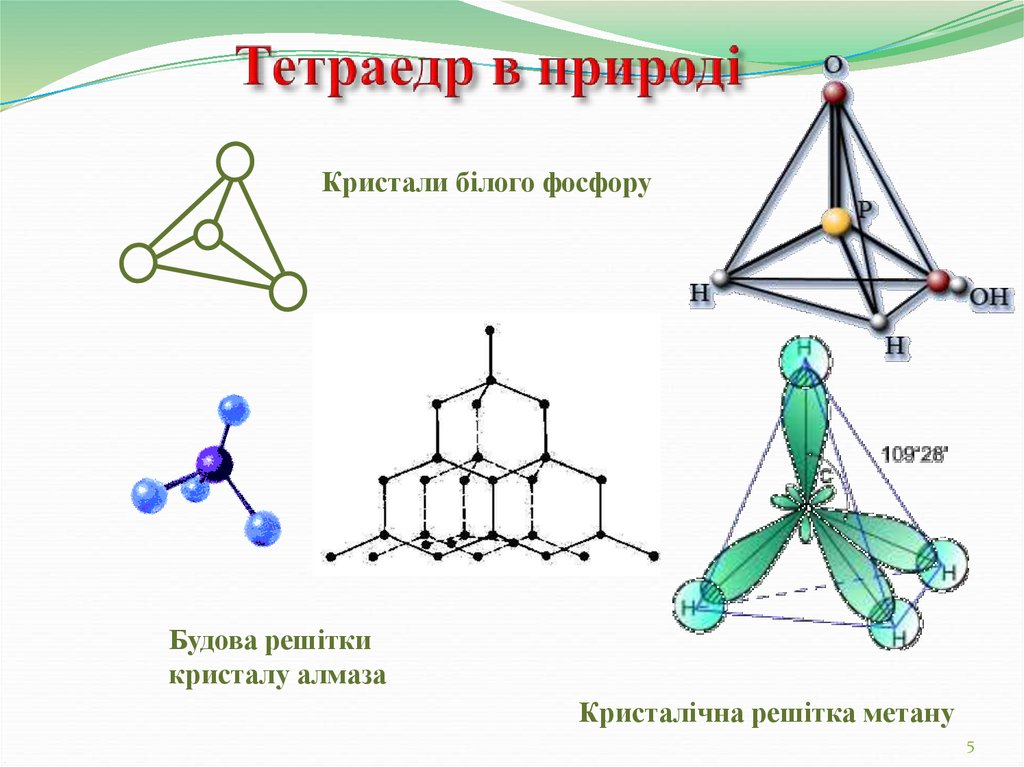
Кристали білого фосфору
Будова решітки
кристалу алмаза
Кристалічна решітка метану
5

6.

Вуглець С
характеризується
структурою октаедра
Кристали
алмаза
6

7.

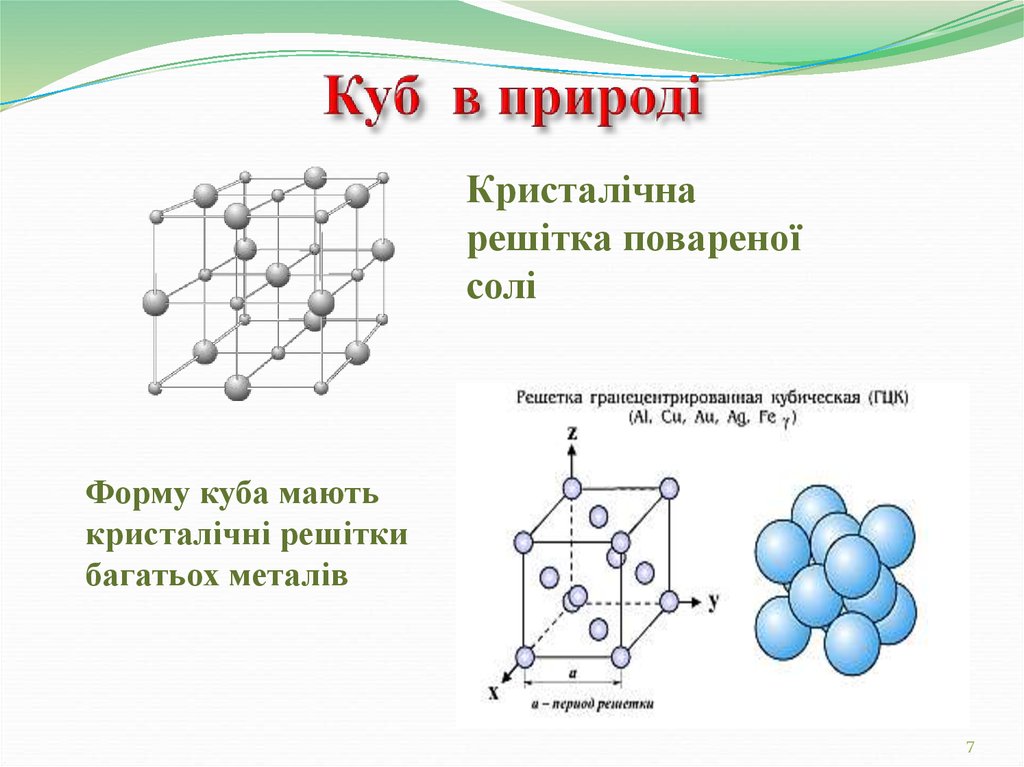
Кристалічна
решітка повареної
солі
Форму куба мають
кристалічні решітки
багатьох металів
7

8.

• Кристал бору має форму ікосаедра
•У біології німецький біолог
початку ХХ століття Еге Геккель
дослідив,що одноклітинні
організми – феодарії, точно
передають форму ікосаедра
•У фізиці капсиди багатьох вірусів
(наприклад бактеріофаги, мімівірус)
8

9.

Вірус поліомієліту
Репродукція картини С.Далі
“ Тайна вечеря ”
Молекула ДНК складається з взаємовідносин ікосаедрів
та додекаедрів
9

10.

октаедр
тетраедр
ікосаедр
додекаедр
10

11.

12.

13.

Архітектура

14.

15.

16.

17.

18.

19.

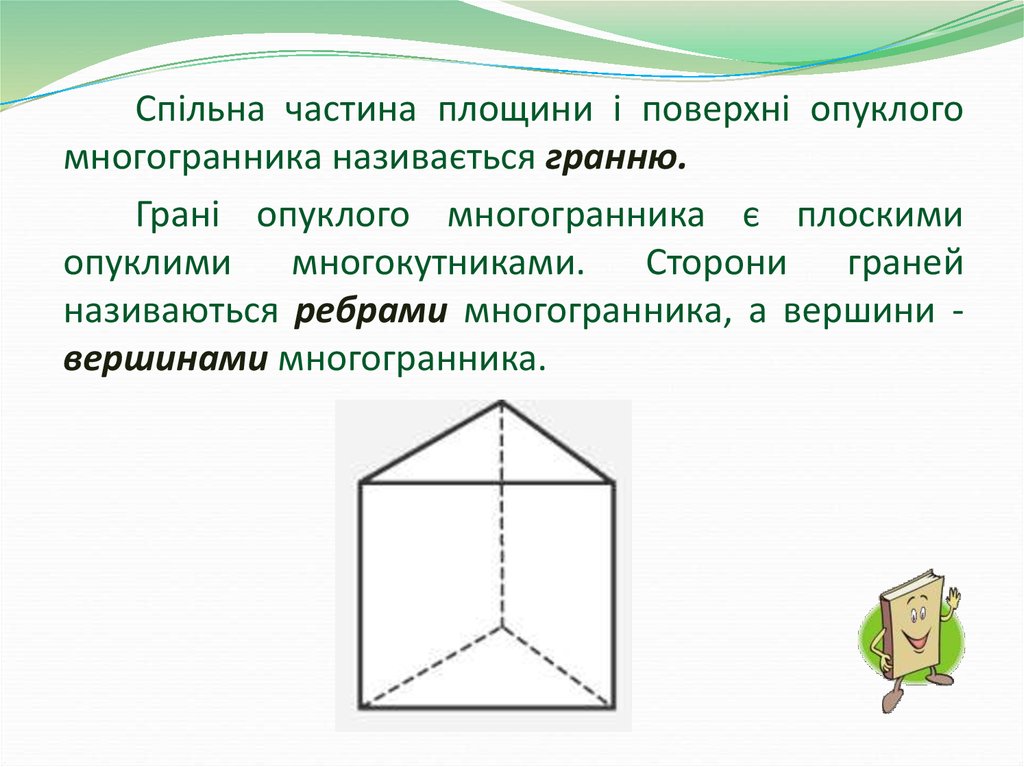
Спільна частина площини і поверхні опуклого
многогранника називається гранню.
Грані опуклого многогранника є плоскими
опуклими многокутниками. Сторони граней
називаються ребрами многогранника, а вершини вершинами многогранника.

20. Усні вправи

На рисунку зображено прямокутний паралелепіпед:
а) назвіть відрізки, паралельні відрізку ВС;
б) назвіть прямі, які перетинаються з прямою, що містить відрізок ВС;
в) назвіть площину, паралельну площині грані АА1В1В;
г) назвіть дві пари перпендикулярних площин;

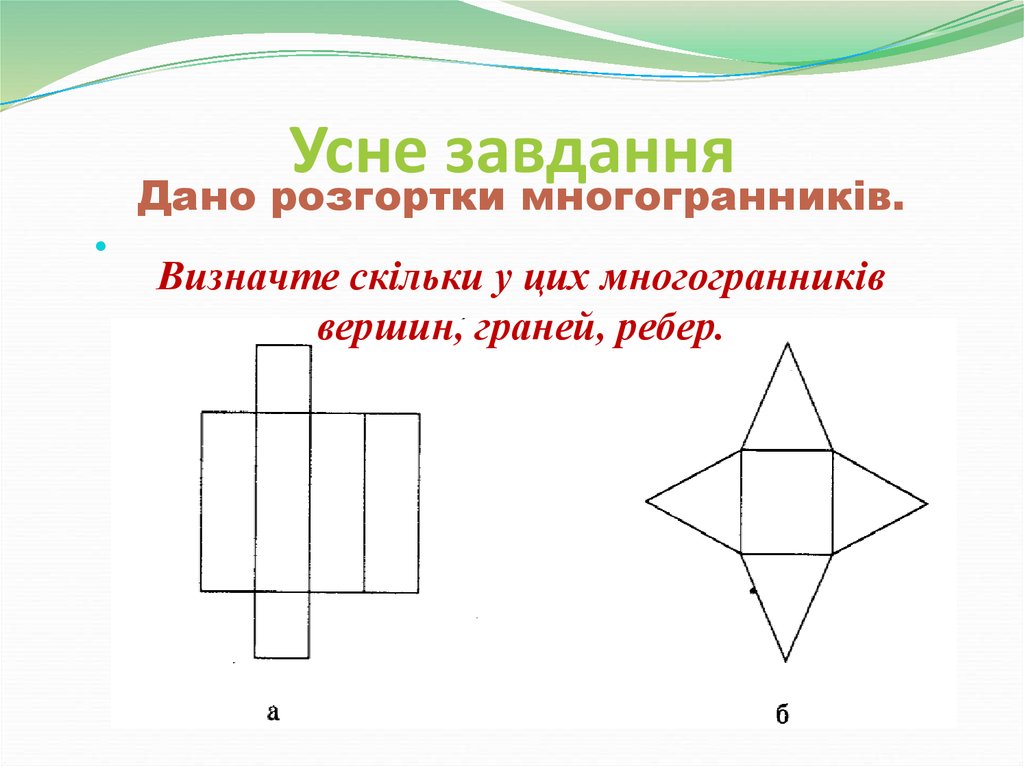
21. Усне завдання

Дано розгортки многогранників.
Визначте скільки у цих многогранників
вершин, граней, ребер.

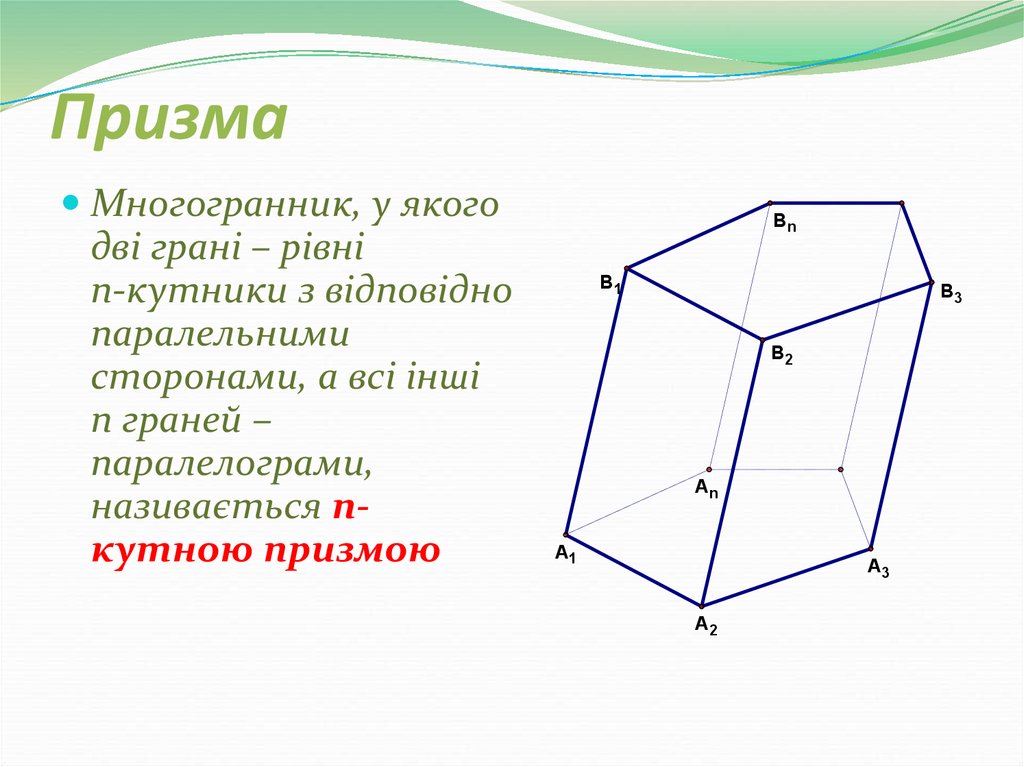
22. Призма

Многогранник, у якого
дві грані – рівні
n-кутники з відповідно
паралельними
сторонами, а всі інші
n граней –
паралелограми,
називається nкутною призмою
Bn
B1
B3
B2
An
A1
A3
A2

23.

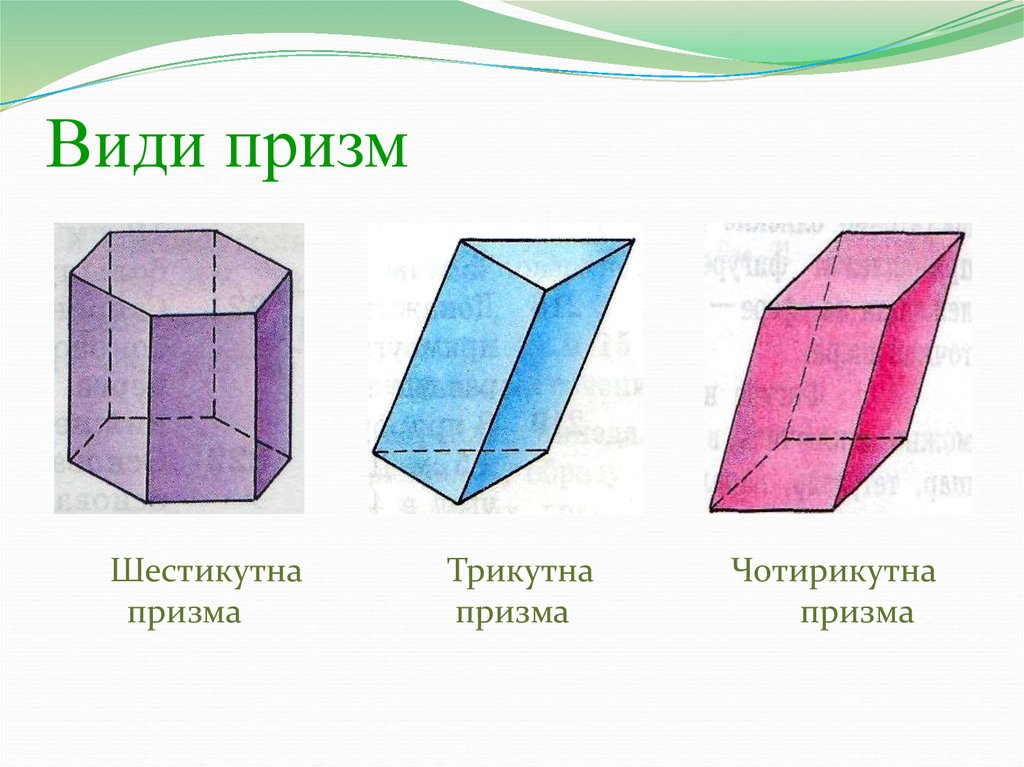
24. Види призм

Шестикутна
призма
Трикутна
призма
Чотирикутна
призма

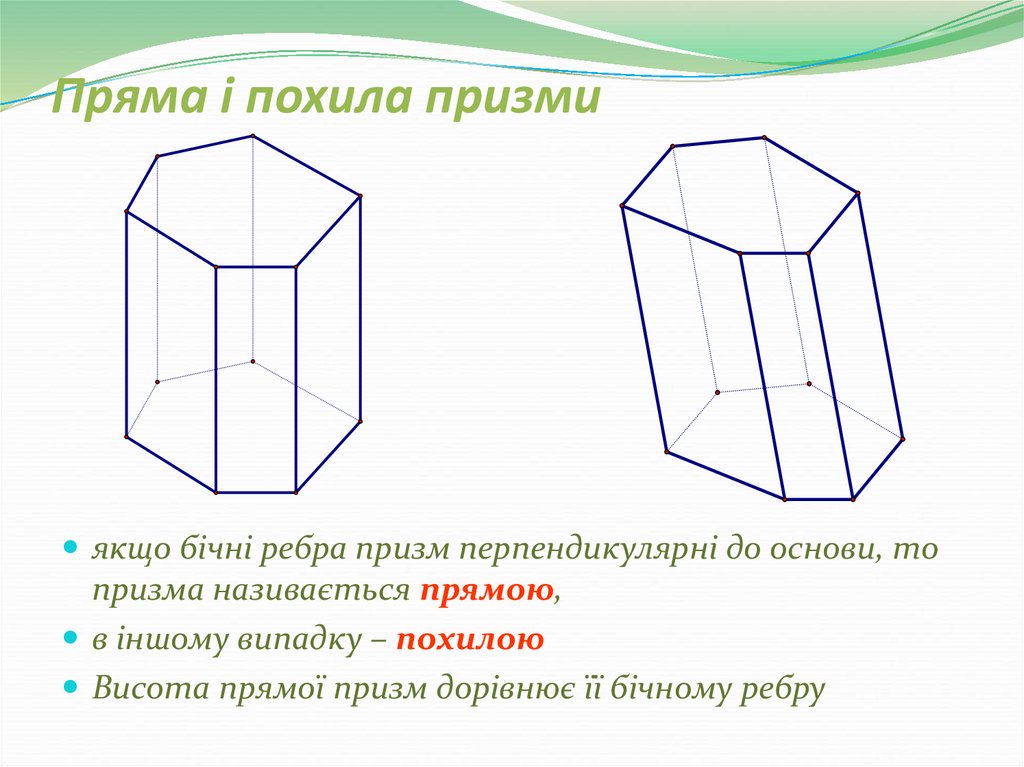
25. Пряма і похила призми

якщо бічні ребра призм перпендикулярні до основи, то
призма називається прямою,
в іншому випадку – похилою
Висота прямої призм дорівнює її бічному ребру

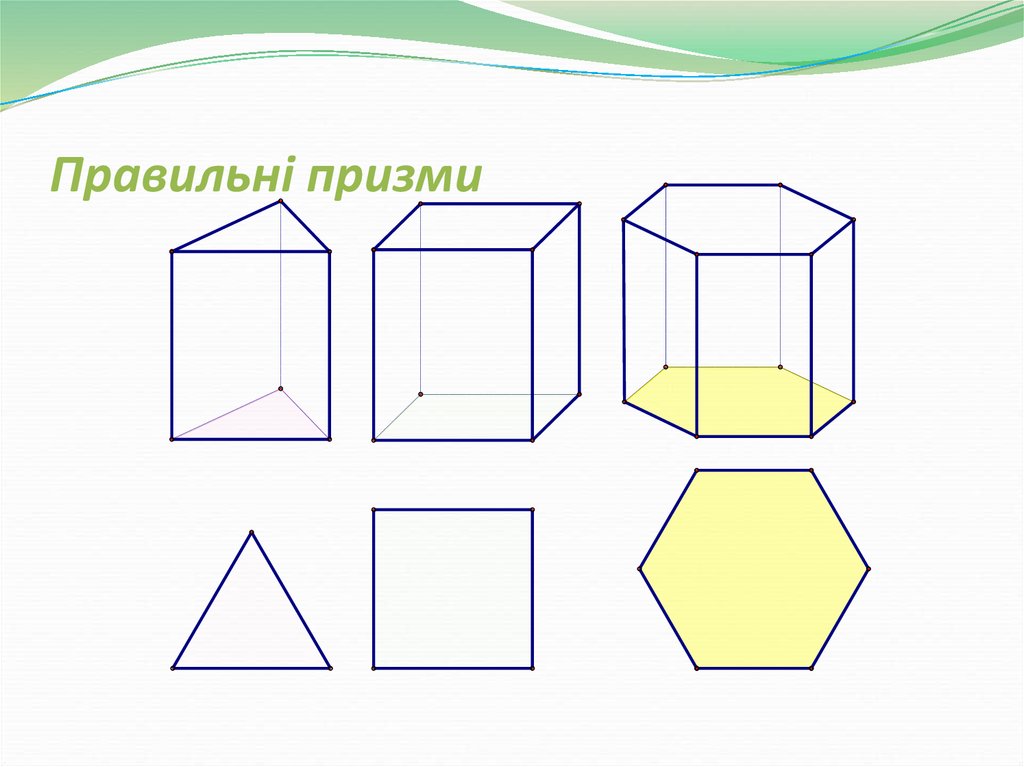
26. Правильна призма

Пряма призма
називається
правильною, якщо її
основи – правильні
многокутники
У правильної призми
всі бічні грані – рівні
прямокутники

27. Правильні призми

28.

Bn
B1
B3
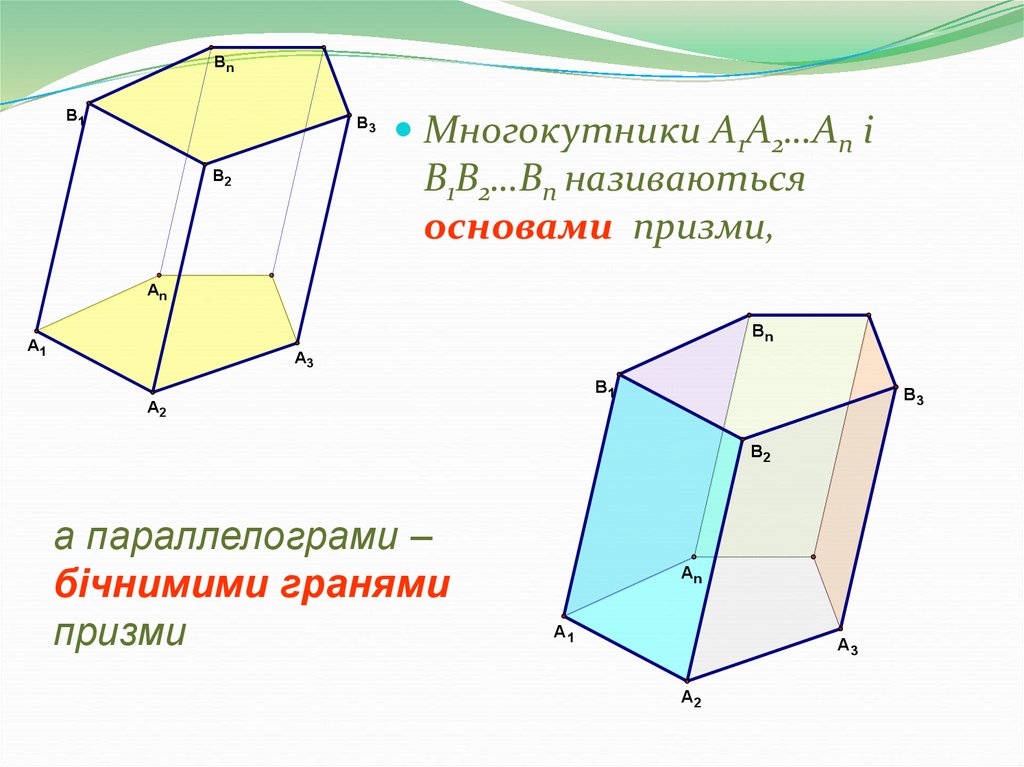
Многокутники A1A2…An і
B1B2…Bn називаються
основами призми,
B2
An
Bn
A1
A3
B1
B3
A2
B2
а параллелограми –
бічнимими гранями
призми
An
A1
A3
A2

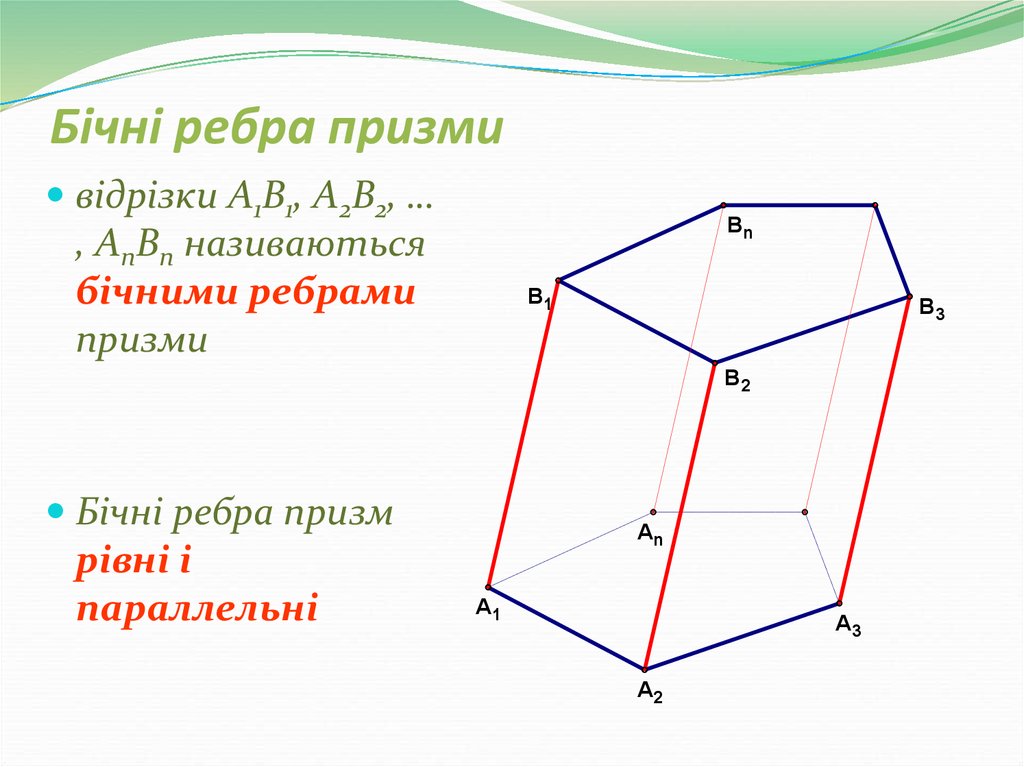
29. Бічні ребра призми

відрізки A1B1, A2B2, …
, AnBn називаються
бічними ребрами
призми
Bn
B1
B3
B2
Бічні ребра призм
рівні і
параллельні
An
A1
A3
A2

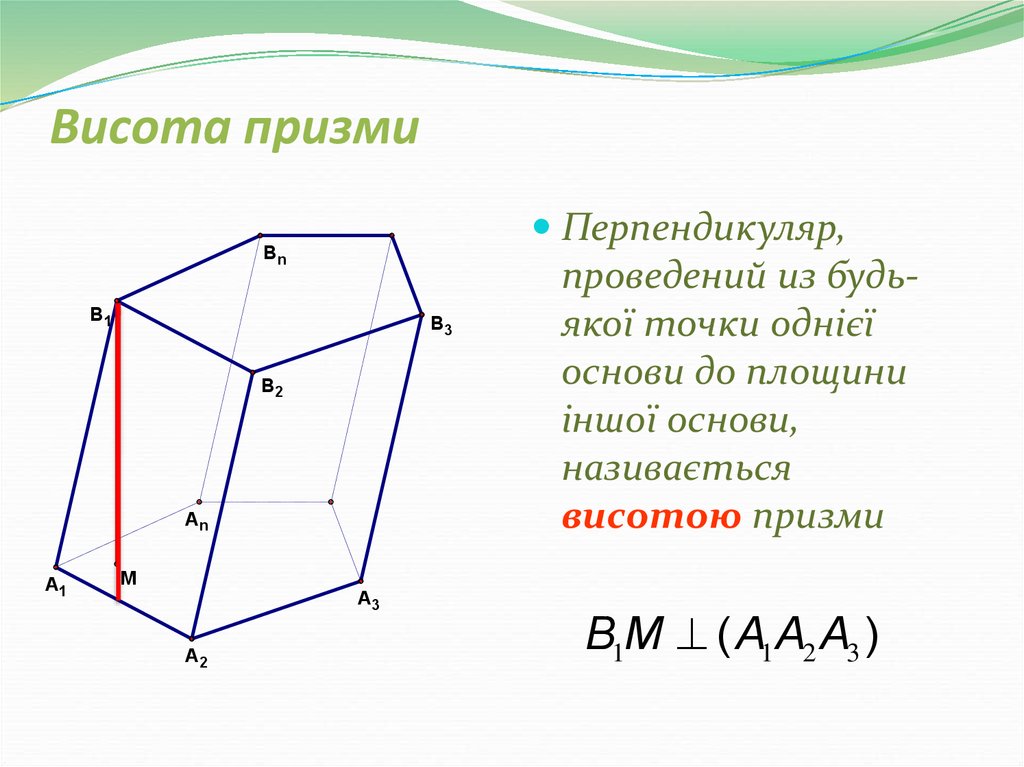
30. Висота призми

Bn
B1
B3
B2
An
A1
Перпендикуляр,
проведений из будьякої точки однієї
основи до площини
іншої основи,
називається
висотою призми
M
A3
A2
B1M ( A1A2 A3 )

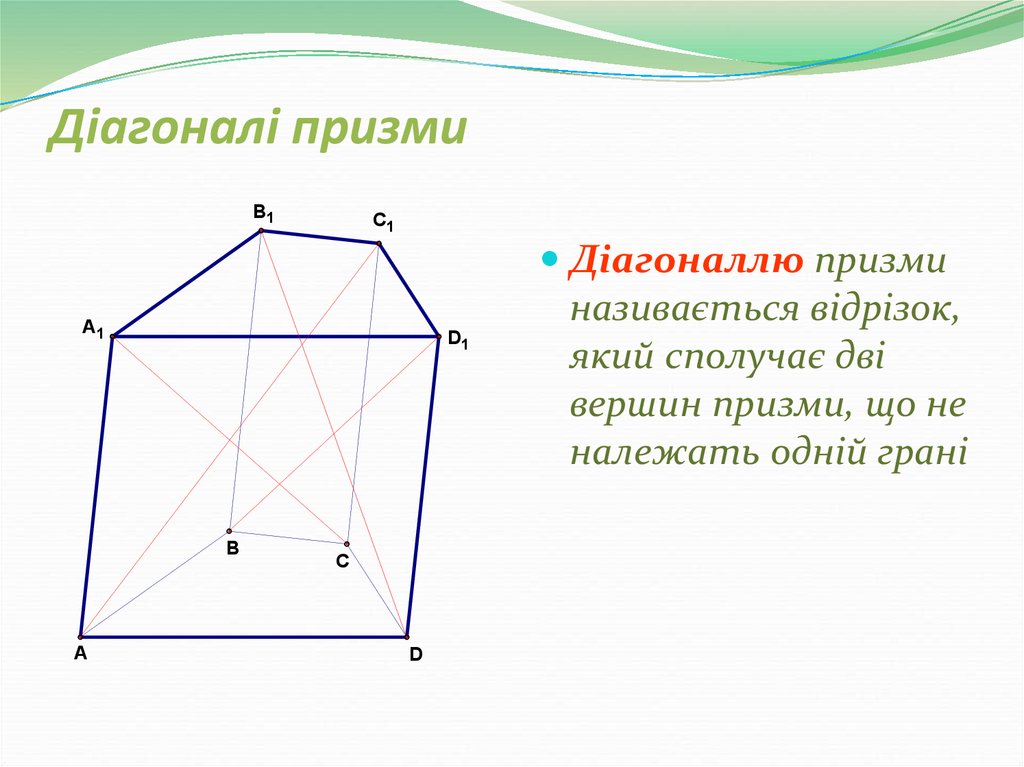
31. Діагоналі призми

B1
C1
A1
D1
B
A
C
D
Діагоналлю призми
називається відрізок,
який сполучає дві
вершин призми, що не
належать одній грані

32. Діагональні перерізи призм

Переріз призми
площиною, яка
проходить через два
бічних ребра, які не
належать одній грані,
називається
діагональним
перерізом
D
E1
D
E1
A1
A1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
C
C
Діагональні перерізи
B1
B1
призми є
паралелограми
E
E
D
A
A
C
C
B
D
B

33. Правила зображення призми

побудувати зображення основи призми;
зобразити бічні ребра у вигляді
паралельних і рівних відрізків;
з’єднати послідовно їх вільні кінці.
невидимі ребра зображають штриховими
лініями.

34. Елементи призми

35. Площа поверхні призми

36. Теорема про площу бічної поверхні прямої призми

37. Площа бічної поверхні похилої призми

Щоб знайти площу бічної поверхні похилої
призми, треба знайти площу кожної її бічної
грані та результати додати
Теорема.
Площа бічної поверхні похилої призми
дорівнює добутку периметра
перпендикулярного перерізу на бічне
ребро призми

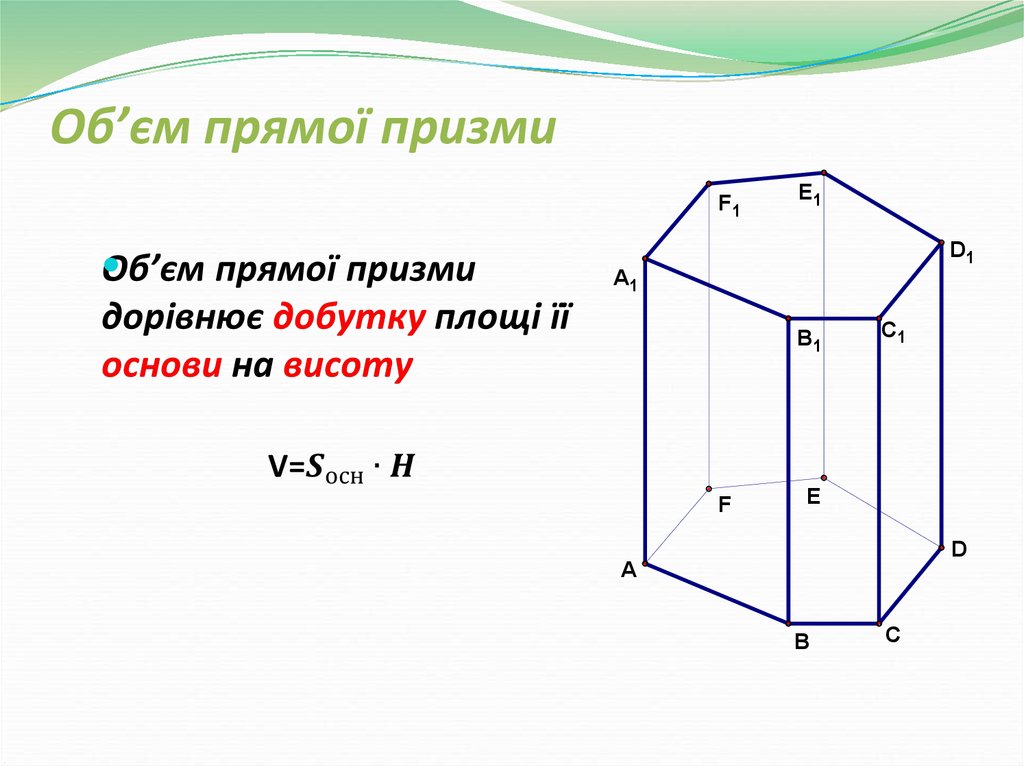
38. Об’єм прямої призми

F1
E1
D1
A1
B1
F
C1
E
D
A
B
C