Похожие презентации:
Механические колебания и волны
1. Механические колебания и волны
1. Гармонические колебания2. Математический маятник
3. Физический маятник
4. Энергия гармонического
колебания
2.
1. Гармонические колебанияКолебаниями называются процессы, отличающиеся той или иной степенью
повторяемости.
В зависимости от физической природы повторяющегося процесса различают
колебания: механические, электромагнитные, электромеханические и т. д.
В зависимости от характера воздействия, оказываемого на колеблющуюся
систему, различают свободные (или собственные) колебания, вынужденные
колебания, автоколебания и параметрические колебания.
Свободными или собственными называются такие колебания, которые
происходят в системе, предоставленной самой себе после того, как ей был
сообщен толчок, либо она была выведена из положения равновесия.
Простейшими являются гармонические колебания, т. е. такие колебания,
при которых колеблющаяся величина изменяется со временем по закону
синуса или косинуса.
Колебания называются периодическими, если значения физических
величин, изменяющихся в процессе колебаний, повторяются через
равные промежутки времени.
3.
2π 1T
ω0 ν
Т – период колебаний – минимальный промежуток времени,
по истечении которого повторяются значения всех
физических величин, характеризующих колебание.
Частота колебаний определяется, как число полных
колебаний в 1 секунду.
ω – циклическая (круговая) частота – число
полных колебаний за 2π секунд.
1
ν
T
2
2
T
4.
Рассмотрим систему, состоящую изшарика массы m, подвешенного на
пружине.
В состоянии равновесия сила mg
уравновешивается упругой силой
k l0:
(1)
0
mg k l
Если сместить шарик от положения
равновесия на расстояние, равное
х, то удлинение пружины станет
равным l0 + х
Проекция результирующей силы на
ось х :
f mg k ( l0 x)
Учитывая условие равновесия (1),
получим, что
f k l0 k l0 kx f kx
5.
Знак «—» в формуле отражает то обстоятельство, что смещение и силаимеют противоположные направления.
Таким образом, сила f обладает следующими свойствами: 1) она
пропорциональна смещению шарика из положения равновесия, 2) она
всегда направлена к положению равновесия.
Силы такого вида, независимо от их природы, принято называть
квазиупругими.
Для того, чтобы сообщить системе смещение х,
нужно совершить против квазиупругой силы работу :
x
kx2
A kxdx
2
0
Эта работа идет на создание запаса потенциальной энергии
системы. Следовательно, система, в которой действует
квазиупругая сила, при смещении из положения равновесия
на расстояние х обладает потенциальной энергией:
kx2
Еp
2
6.
Сообщим шарику смещение х=d, после чего предоставим систему самой
себе. Под действием силы f = -kx шарик будет двигаться к положению
равновесия со все возрастающей скоростью
x
При этом потенциальная энергия системы будет убывать ,
но зато появится все возрастающая кинетическая энергия
(массой пружины пренебрегаем).
mx 2
Ek
2
Придя в положение равновесия, шарик продолжает двигаться по инерции.
Это движение будет замедленным и прекратится тогда, когда кинетическая
энергия полностью превратится в потенциальную, т. е. когда смещение
шарика станет равным - d. Затем такой же процесс будет протекать при
движении шарика в обратном направлении.
Если трение в системе отсутствует, энергия системы должна сохраняться и
шарик будет двигаться в пределах от х = d до х = - d.
7.
Любому колебательному процессу присуще:1) Наличие положения равновесия
2) Наличие возвращающей силы
3) Наличие инерции колеблющегося тела
Запишем второй закон Ньютона для шарика:
m x kx
обозначим
k
x x 0
m
k
02
m
F ma m x
x 02 x 0
F kx
уравнение колебаний
шарика на пружине
Решение уравнения колебаний имеет вид:
x A cos 0t
или
x A sin 0t
Смещение х изменяется со временем по закону косинуса. Следовательно,
движение системы, находящейся под действием силы вида f = —kx,
представляет собой гармоническое колебание.
2
8.
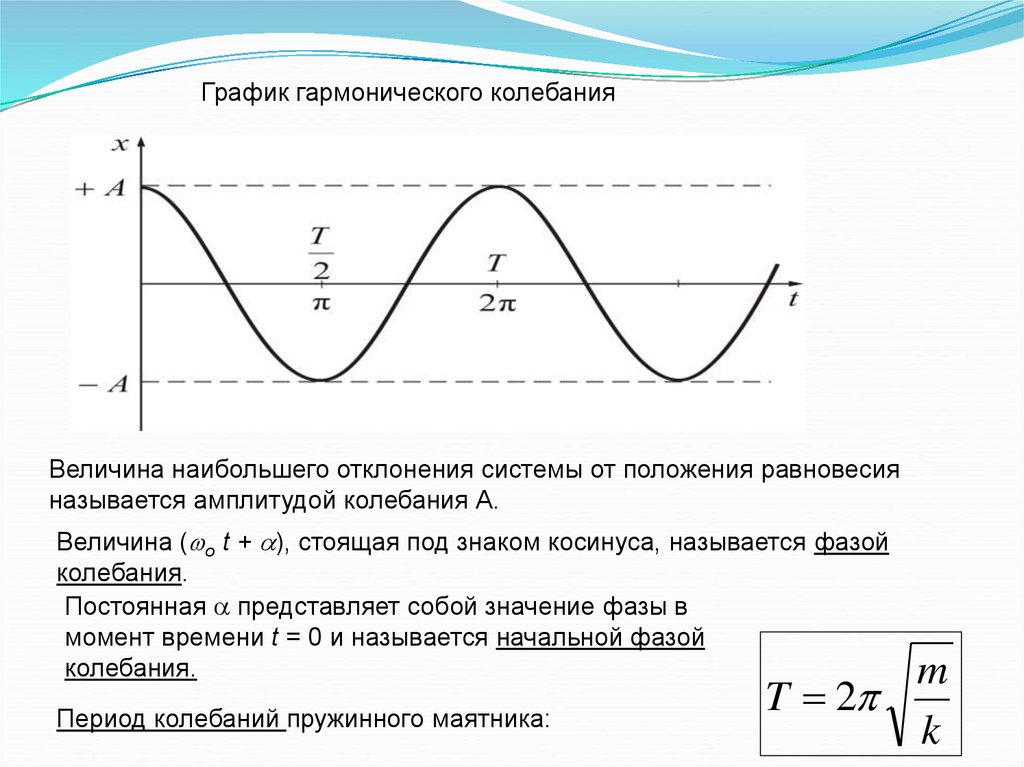
График гармонического колебанияВеличина наибольшего отклонения системы от положения равновесия
называется амплитудой колебания А.
Величина ( o t + ), стоящая под знаком косинуса, называется фазой
колебания.
Постоянная представляет собой значение фазы в
момент времени t = 0 и называется начальной фазой
колебания.
Период колебаний пружинного маятника:
m
T 2
k
9.
Скорость и ускорение гармонического колебанияСмещение описывается уравнением
x Acos( 0t )
Продифференцировав по времени выражение x(t), получим выражение
для скорости
x A 0sin ( 0t ) A 0 cos( 0t )
0sin ( 0t 0 )
где
0 A 0
2
– амплитуда скорости;
Продифференцировав по времени выражение (t), получим выражение
для ускорения
a x A 02cos( 0t )
a a0cos( 0t 0 )
где
a0 A 02
– амплитуда ускорения.
10.
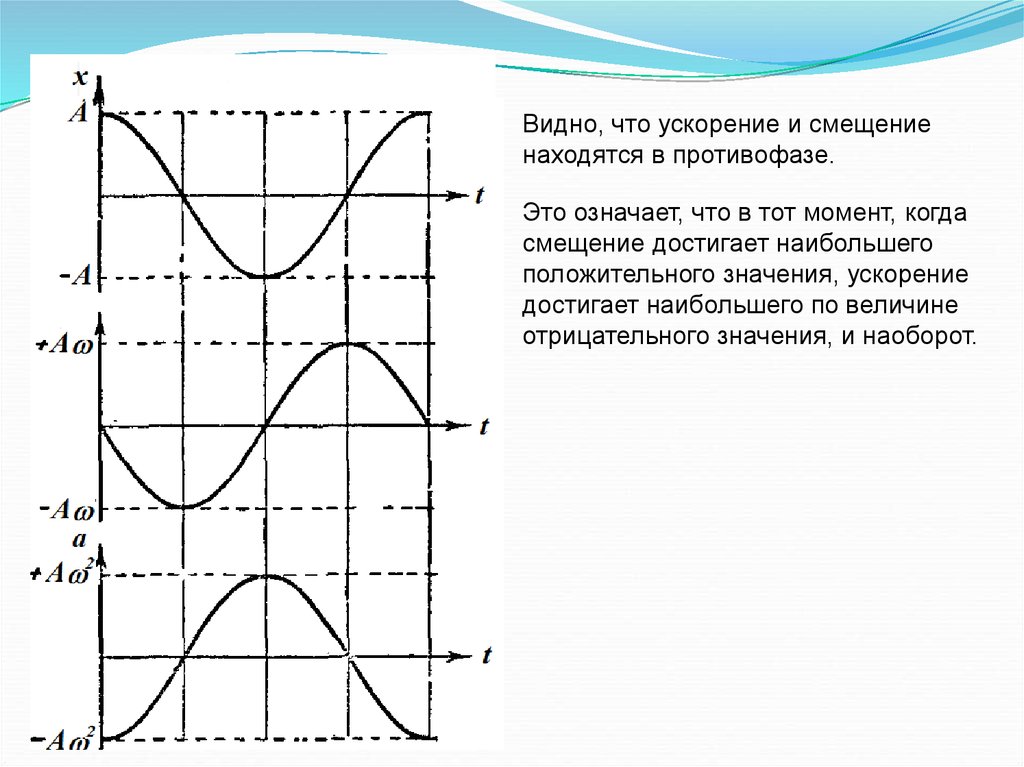
Видно, что ускорение и смещениенаходятся в противофазе.
Это означает, что в тот момент, когда
смещение достигает наибольшего
положительного значения, ускорение
достигает наибольшего по величине
отрицательного значения, и наоборот.
11.
2. Математический маятникl
Математическим маятником называют
идеализированную систему.
Математический маятник –
материальная точка, подвешенная на
невесомой нерастяжимой нити и
совершающая движение в вертикальной
плоскости под действием силы тяжести.
При отклонении маятника от положения
равновесия возникает вращательный
момент М.
M mgl sin
lsin
mg
Запишем для маятника уравнение динамики вращательного
2
движения.
I
ml
;
I M Учтем, что
Получим:
ml mgl sin
2
или
12.
gsin 0
l
Получим:
Получим:
Ограничимся рассмотрением малых колебаний
g
0
l
sin
Обозначим:
2
0 0
Решение этого уравнения имеет вид:
0
g
2
0
l
A cos( 0t )
(гармонические колебания)
- частота колебаний математического маятника
l
T 2
g
- период колебаний математического маятника
13.
3. Физический маятникФизическим маятником называется твердое тело,
способное совершать колебания вокруг неподвижной
точки, не совпадающей с его центром инерции.
При отклонении маятника от положения
равновесия возникает вращательный момент:
M mgl sin
где m – масса маятника; l – расстояние между
точкой подвеса и центром инерции маятника.
Запишем для маятника уравнение динамики
вращательного движения. I M
I mgl sin
В случае малых колебаний
I mgl
или
14.
mgl0
I
I
T 2
mgl
l
T 2
g
l пр
или
0
2
0
где
mgl
I
2
0
- период колебаний физического маятника
Из сопоставления формул получается,
что математический маятник с длиной
будет иметь такой период колебаний,
как и данный физический маятник.
- приведенная длина физического маятника.
I
lпр
ml
15.
4. Энергия гармонического колебанияКвазиупругая сила является консервативной. Поэтому полная энергия
гармонического колебания должна оставаться постоянной.
x A cos( t 0 ); A sin( t 0 )
m 2 mA2 2 sin 2 ( t 0 )
Ek
2
2
Ek max
mA2 2
2
kx2 kA2 cos 2 ( t 0 ) mA2 2 cos 2 ( t 0 )
Ep
2
2
2
E p max
mA2 2
2
2 2
mA2 2
mA
2
2
E E p Ek
cos ( t 0 ) sin ( t 0 )
2
2
16.
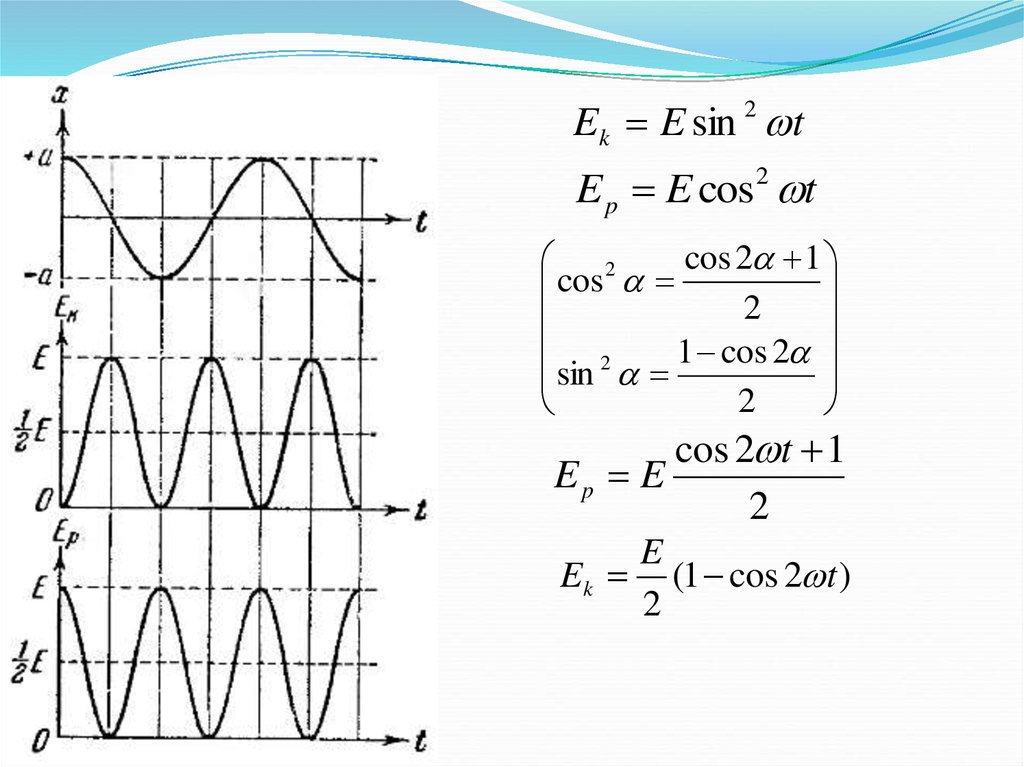
Ek E sin 2 tE p E cos 2 t
cos 2 1
2
cos
2
2
1 cos 2
sin
2
cos 2 t 1
Ep E
2
E
Ek (1 cos 2 t )
2
17.
1.Затухающие колебания2.Вынужденные колебания
3.Автоколебания
18.
1. Затухающие колебанияЗатухающими называются колебания, энергия которых
уменьшается с течением времени.
Рассмотрим свободные затухающие колебания.
Ограничимся рассмотрением малых колебаний.
fr ~
f r r rx
r – коэффициент
сопротивления
Напишем для колеблющегося тела 2-ой закон Ньютона:
m x kx rx
x 2 x x 0
2
0
x
или
(*)
где
Будем искать решение уравнения в виде:
где А(t) – некоторая функция времени.
k
r
x x 0
m
m
r
k
2
2 ; 0
m
m
x A(t ) cos( t )
19.
Продифференцируем по t, найдемx и
x
x A (t ) cos( t ) A(t ) sin( t )
(t ) cos( t ) A (t ) sin( t )
x A
A (t ) sin( t ) A(t ) 2 cos( t )
(t ) cos( t ) 2 A (t ) sin( t )
x A
A(t ) 2 cos( t )
и x в x 2 x 02 x 0
подставляя x
(t ) cos( t ) 2 A (t ) sin( t )
A
получим:
A(t ) cos( t ) 2 A (t ) cos( t )
2
2 A(t ) sin( t ) 02 A(t ) cos( t ) 0
20.
(t ) A(t ) 2 2 A (t ) 2 A(t )]cos( t )[ A
0
sin( t )[2 A (t ) 2 A(t ) ] 0
(t ) 2 A (t ) ( 2 2 ) A(t )] cos( t )
[A
0
2 [ A (t ) A(t )] sin( t ) 0
I
II
A (t ) A(t ) 0
A (t ) 2 A (t ) ( 2 2 ) A(t ) 0
0
I уравнение можно представить в виде:
Проинтегрируем и получим:
ln A t ln A0
где
dA
A
dt
ln A0
dA
dt
A
- постоянная интегрирования
21.
Произведя потенцирование, получимA(t ) A0 e t
- зависимость амплитуды свободных
затухающих колебаний от времени
t
A(t ) A0 e A
подставим в уравнение II, получим:
A (t ) A 2 e t A 2
0
(разделим на А)
A 2 2 2 A ( 02 2 ) A 0
2 2 2 02 2 0 2 02 2 0
2 02 2
При условии, что
- частота затухающих колебаний
02 2 ,
величина будет вещественной
Т.о. при небольшом затухании решение уравнения:
x A0 e
t
cos( t )
22.
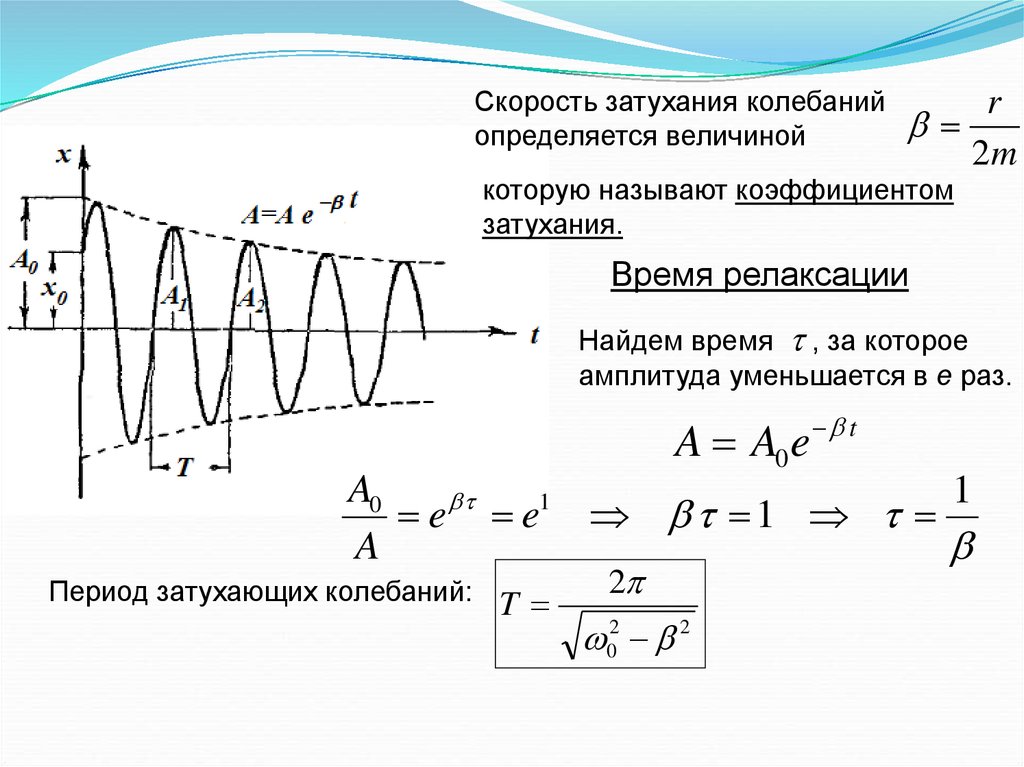
Скорость затухания колебанийопределяется величиной
r
2m
которую называют коэффициентом
затухания.
Время релаксации
Найдем время , за которое
амплитуда уменьшается в е раз.
A A0 e
t
A0
1
1
e e 1
A
Период затухающих колебаний:
T
2
02 2
23.
Отношение двух последующих амплитуд называют декрементомзатухания:
D=1 – гармонические колебания;
A(t )
D
e T
A(t T )
D>1 – затухающие колебания;
D< 1 – колебания с возрастающей амплитудой;
D - апериодическое движение
Логарифм отношения двух последующих амплитуд называется
логарифмическим декрементом затухания:
A(t )
ln
T
A(t T )
Q N e
T
- добротность колебательной системы
24.
2. Вынужденные колебанияВынужденными называются колебания, возникающие в
колебательной системе под действием внешней
периодически изменяющейся силы (вынуждающей силы).
Пусть вынуждающая сила изменяется со временем по гармоническому
закону:
f F0 cos t
Предполагая колебания достаточно малыми, будем считать силу
сопротивления пропорциональной скорости.
Тогда уравнение движения:
0
m x kx rx F cos t
F0
k
r
x x x cos t
m
m
m
x 2 x 02 x f 0 cos t
k
02 ;
m
(*)
r
2 ;
m
F0
f0
m
Неоднородное линейное
дифференциальное уравнение
второго порядка.
25.
tx A0 e cos( ' t ' )
Найдем частное решение уравнения (*) в виде: x A cos( t )
x A sin( t ) x A 2 cos( t )
2
x
2
x
x в уравнение
Подставим x и
0 x f 0 cos t
Общее решение однородного уравнения:
A 2 cos( t ) 2 A sin( t ) 02 A cos( t ) f 0 cos t
A 2 (cos t cos sin t sin ) 2 A (sin t cos cos t sin )
02 A(cos t cos sin t sin ) f 0 cos t
2
2
cos
t
(
A
cos
2
A
sin
0 A cos f 0 )
2
2
sin
t
(
A
sin
2
A
cos
0 A sin )
2
2
A
cos
2
A
sin
(I )
0 A cos f 0
2
2
A
sin
2
A
cos
( II )
0 A sin 0
26.
Из II уравнения:sin ( 02 A A 2 ) 2 A cos
2 A
2
tg 2
2
2
0 A A
0 2
tg
A( 02 2 ) cos 2 A sin f 0
A( 02 2 ) sin 2 A cos 0
2
02 2
I
II
Возведем I и II уравнения в квадрат:
A2 ( 02 2 ) 2 cos 2 2 A( 02 2 ) cos 2 A sin
2 2 2
2
2
4
A
sin
f
0
2 2
2 2
2
2
2
A
(
)
sin
2
A
(
) sin 2 A cos
0
0
4 2 A2 2 cos 2 0
Складываем уравнения:
27.
A2 ( 02 2 ) 2 4 2 A2 2 f 02A [( ) 4 ] f
2
2
0
2 2
2
2
2
0
Амплитуда вынужденных колебаний
A
f0
( 02 2 ) 2 4 2 2
Т.о. частное решение:
2
(1)
x
cos t arctg 2
2
0
( 02 2 ) 2 4 2 2
f0
Общее решение кроме частного решения, содержит решение
однородного уравнения:
t
x A0 e
cos( ' t ' )
Т.о., функция (1) описывает установившиеся вынужденные колебания.
28.
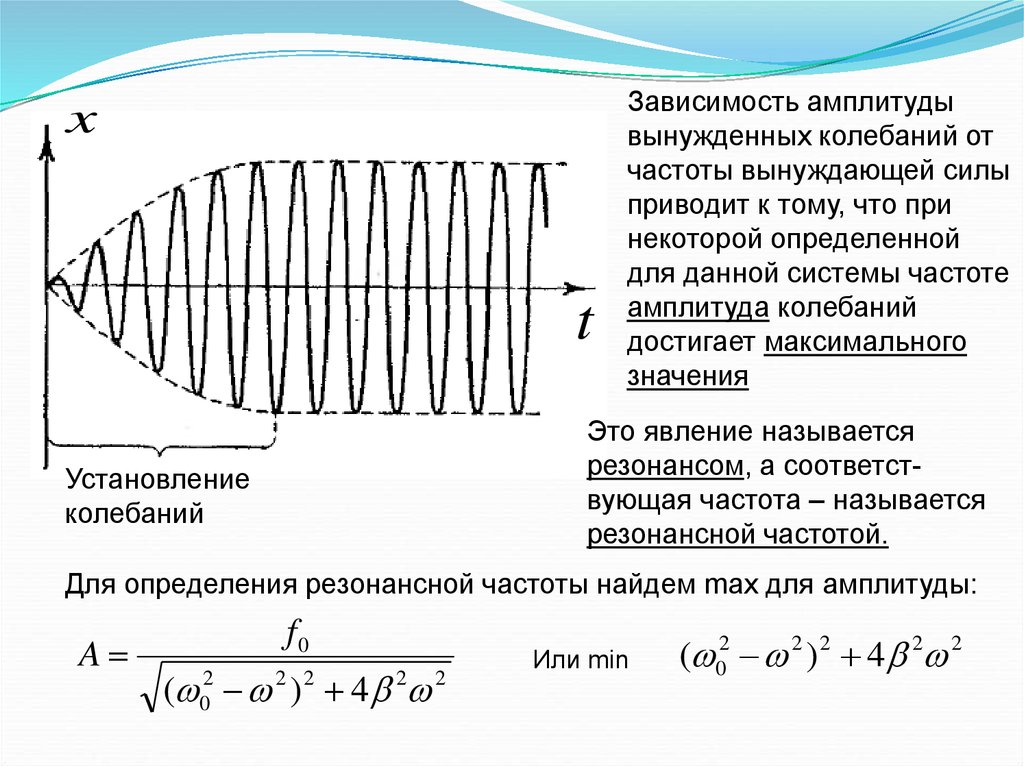
xt
Зависимость амплитуды
вынужденных колебаний от
частоты вынуждающей силы
приводит к тому, что при
некоторой определенной
для данной системы частоте
амплитуда колебаний
достигает максимального
значения
Это явление называется
резонансом, а соответствующая частота – называется
резонансной частотой.
Установление
колебаний
Для определения резонансной частоты найдем max для амплитуды:
A
f0
( 02 2 ) 2 4 2 2
Или min
( 02 2 ) 2 4 2 2
29.
Продифференцировав подкоренное выражение по иприравняв нулю, получим условие , определяющее рез:
4( 02 2 ) 8 2 0
Это уравнение имеет три решения:
I
0
02 2 2
II и III
I решение ( =0) соответствует максимуму знаменателя.
Для резонансной частоты получается одно значение:
рез 02 2 2
Подставим в выражение для амплитуды и получим выражение для
амплитуды при резонансе:
f0
Aрез
( 2 ) 4 ( 2 )
2
0
2
0
2 2
f0
4 4 8
4
2
2
0
4
2
2
0
2
f0
4 2 02 4 4
30.
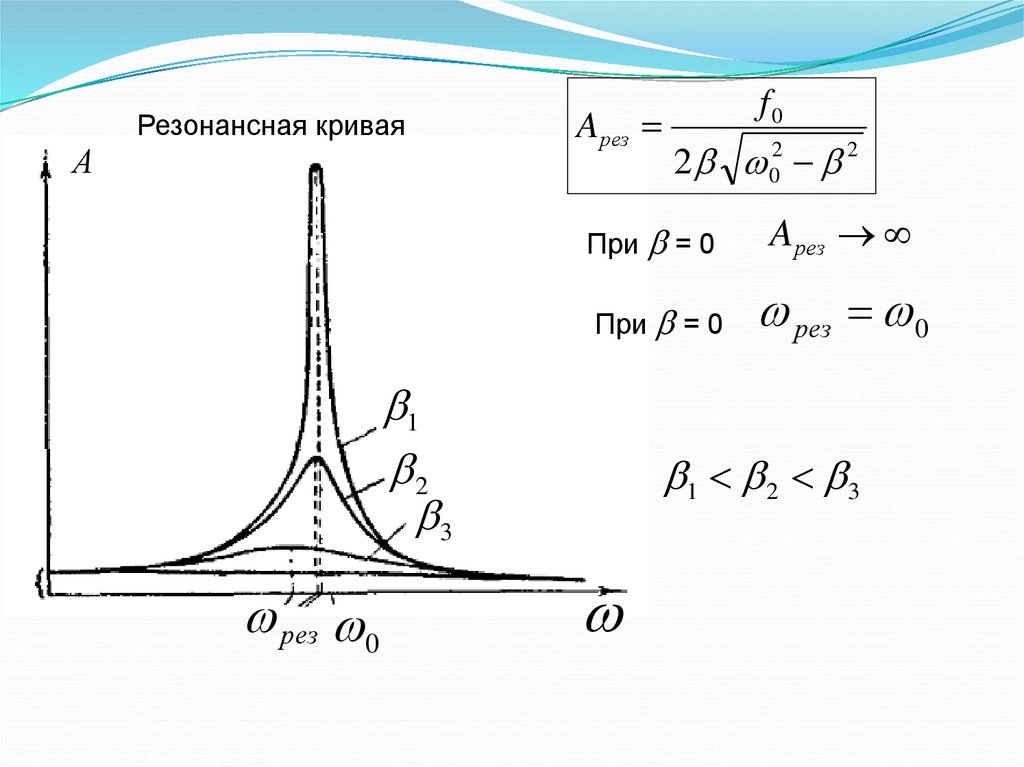
Резонансная криваяА
Aрез
2 02 2
При = 0
Aрез
При = 0
рез 0
1
2
3
рез 0
f0
1 2 3
31.
АвтоколебанияПри затухающих колебаниях энергия системы расходуется на
преодоление сопротивления среды. Если восполнять эту убыль
энергии, колебания станут незатухающими. Пополнение энергии
системы может осуществляться за счет толчков извне, однако эти
толчки должны сообщаться системе в такт с ее колебаниями, в
противном случае они могут ослабить колебания и даже,
прекратить их совсем. Можно сделать так, чтобы колеблющаяся
система сама управляла внешним воздействием, обеспечивая
согласованность сообщаемых ей толчков со своим движением.
Такая система называется автоколебательной, а совершаемые ею
незатухающие колебания — автоколебаниями.
Любая автоколебательная система состоит из 4-х частей.
Обратная связь
Источник энергии
Клапан
Колебательная
система
31


























 Физика
Физика








