Колебания и волны

1.

Курс общей физики
Механика
Лекция №4
Колебания и волны
к.ф.-м.н., доцент ШЕН
Стеблий Максим Евгеньевич
г. Владивосток
2017

2.

Гармонические колебания
Колебания — это повторяющийся во времени процесс изменения
состояний системы около точки равновесия.
Гармонические колебания — колебания, при которых физическая величина
изменяется с течением времени по закону синуса или косинуса.
Рассмотрим систему, состоящую из шарика массы m, подвешенного на
пружине. В состояние равновесия можно записать баланс сил:
mg k l0
Отклонение шарика от положения равновесия описывается изменением
координаты x. В таком случае результирующая сила:
f mg k ( l0 x)
f kx
Для описания движения маятника запишем второй закон Ньютона:
fi ma
kx ma
Представим ускорение, как вторую производную от координаты по
времени и обозначим константы, как ω2:
kx m x m x kx 0 | m
k
k
x 0 02
m
m
2
x 0 x 0
x
Движение шарика описывается линейным однородным
дифференциальным уравнением второго порядка.
Решением такого уравнения может являться уравнение
вида:
x a cos( 0t )
Смещение шарика происходит по закону синуса (или
косинуса), то есть является гармоническим колебанием.
x a cos( 0t )
Отклонение от положения равновесия.
Амплитуда – величина наибольшего отклонения от положения
равновесия.
Фаза – аргумент колебательного процесса, являющийся функцией
времени.
2
Начальная фаза – значение фазы в момент времени t=0.

3.

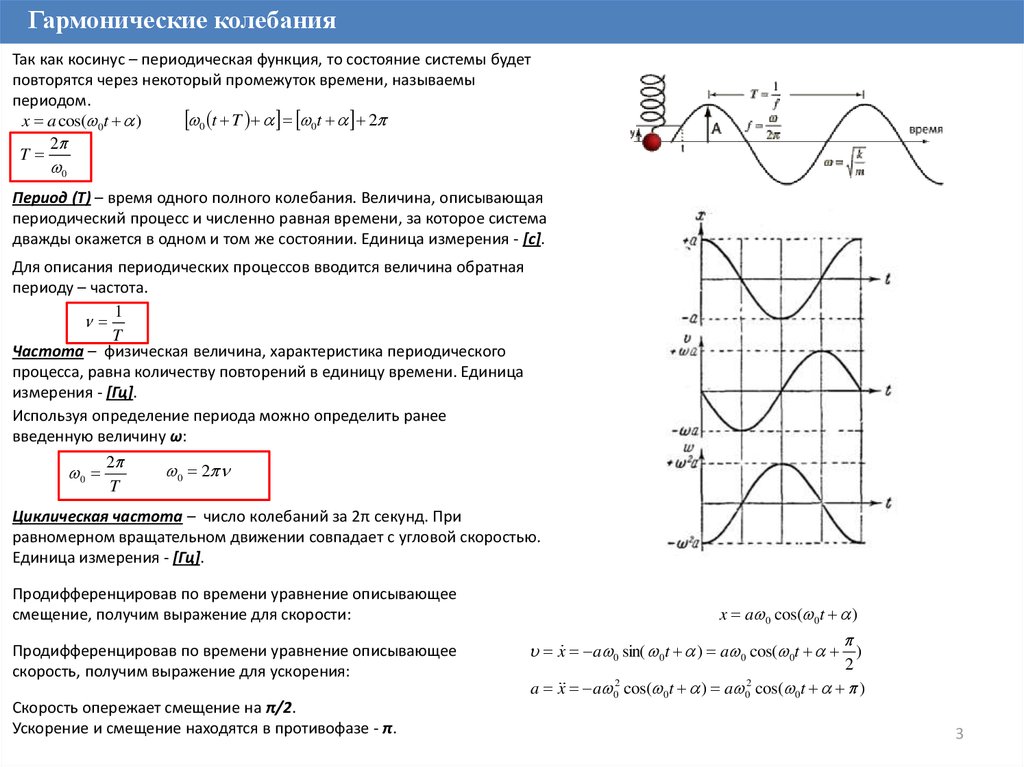
Гармонические колебания
Так как косинус – периодическая функция, то состояние системы будет
повторятся через некоторый промежуток времени, называемы
периодом.
0 t T 0t 2
x a cos( 0t )
2
T
0
Период (T) – время одного полного колебания. Величина, описывающая
периодический процесс и численно равная времени, за которое система
дважды окажется в одном и том же состоянии. Единица измерения - [с].
Для описания периодических процессов вводится величина обратная
периоду – частота.
1
T
Частота – физическая величина, характеристика периодического
процесса, равна количеству повторений в единицу времени. Единица
измерения - [Гц].
Используя определение периода можно определить ранее
введенную величину ω:
0
2
T
0 2
Циклическая частота – число колебаний за 2π секунд. При
равномерном вращательном движении совпадает с угловой скоростью.
Единица измерения - [Гц].
Продифференцировав по времени уравнение описывающее
смещение, получим выражение для скорости:
Продифференцировав по времени уравнение описывающее
скорость, получим выражение для ускорения:
Скорость опережает смещение на π/2.
Ускорение и смещение находятся в противофазе - π.
x a 0 cos( 0t )
x a 0 sin( 0t ) a 0 cos( 0t )
2
a x a cos( 0t ) a cos( 0t )
2
0
2
0
3

4.

Математический маятник
Математический маятник — осциллятор, представляющий собой механическую
систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или
лёгкого стержня и находящуюся в однородном поле сил тяготения.
Отклонение от положения равновесия характеризуется углом ϕ,
образованным нитью с вертикалью. При отклонение от положения
равновесия возникает вращательный момент M, равный:
ϕ
M mgl sin
Момент силы M направлен так, что бы вернуть систему в состояние
равновесия. В данном случае на маятник действует квазиупругая сила.
С силой упругости общее только то, что стремятся вернуть систему в
состояние равновесия.
Запишем основное уравнение динамики вращательного движения с
учетом того, что угловое ускорение β можно представить, как вторую
производную по времени от угла поворота:
M I M I ml 2
g
ml 2 mgl sin sin 0
l
Рассматривая колебания с малым углом отклонения, можно упростить
уравнение:
sin
g
02
l
Определи период колебаний математического
маятника:
02
- собственная частота.
0
2
0
Движение маятника описывается линейным однородным
дифференциальным уравнением второго порядка. Решением такого
уравнения может являться уравнение вида:
a cos( 0t )
Отклонения маятника происходит по закону синуса (или
косинуса), то есть является гармоническим колебанием.
g
l
0
1
T
1
g
2 2
T
l
g
l
2 ;
T 2
1
1
T 2
g
l
l
g
Период определяется только длинной маятника и не
зависит ни от массы ни от величины отклонения (в
4
пределах малых углов).

5.

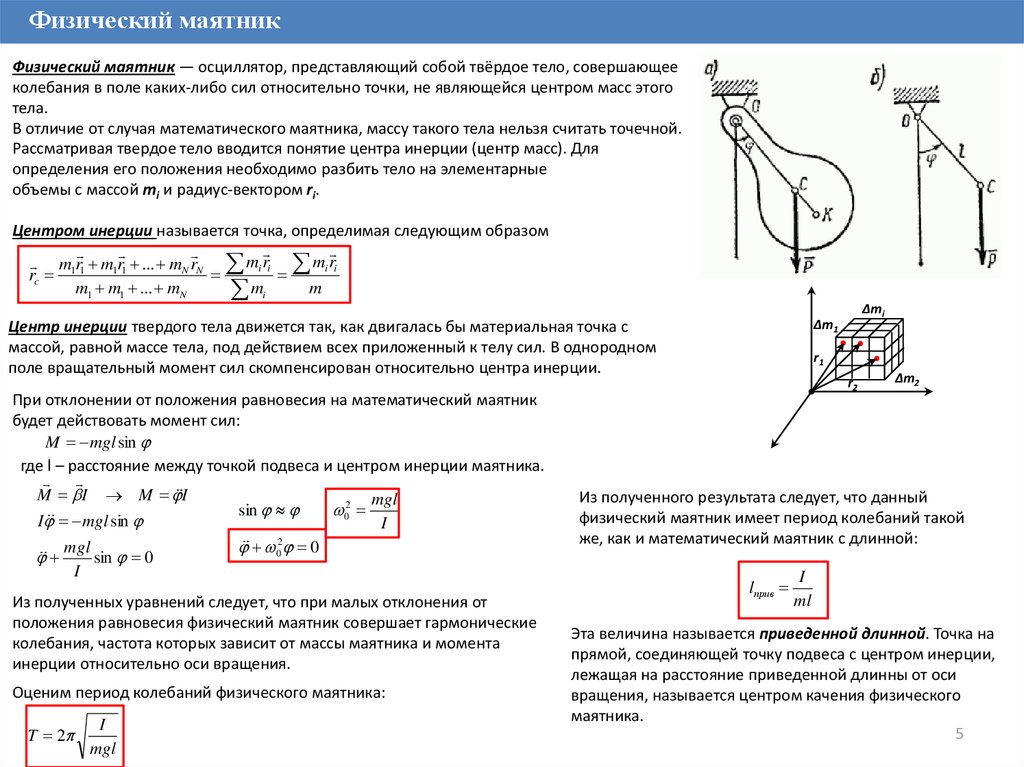
Физический маятник
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее
колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого
тела.
В отличие от случая математического маятника, массу такого тела нельзя считать точечной.
Рассматривая твердое тело вводится понятие центра инерции (центр масс). Для
определения его положения необходимо разбить тело на элементарные
объемы с массой mi и радиус-вектором ri.
Центром инерции называется точка, определимая следующим образом
m1r1 m1r1 ... mN rN mi ri mi ri
rc
m1 m1 ... mN
m
mi
При отклонении от положения равновесия на математический маятник
будет действовать момент сил:
M mgl sin
где l – расстояние между точкой подвеса и центром инерции маятника.
M I M I
mgl
sin
02
I mgl sin
I
2
mgl
0 0
sin 0
I
Из полученных уравнений следует, что при малых отклонения от
положения равновесия физический маятник совершает гармонические
колебания, частота которых зависит от массы маятника и момента
инерции относительно оси вращения.
Оценим период колебаний физического маятника:
T 2
I
mgl
Δmi
Δm1
Центр инерции твердого тела движется так, как двигалась бы материальная точка с
массой, равной массе тела, под действием всех приложенный к телу сил. В однородном
поле вращательный момент сил скомпенсирован относительно центра инерции.
r1
r2
Δm2
Из полученного результата следует, что данный
физический маятник имеет период колебаний такой
же, как и математический маятник с длинной:
lприв
I
ml
Эта величина называется приведенной длинной. Точка на
прямой, соединяющей точку подвеса с центром инерции,
лежащая на расстояние приведенной длинны от оси
вращения, называется центром качения физического
маятника.
5

6.

Затухающие колебания
Гармонические колебания описывались действием только квазиупругих сил. Если в системе
присутствуют диссипативные силы, то колебания со временем будут затухать.
Рассмотрим свободные (нет внешнего периодического воздействия) затухающие колебания. Пусть силы
сопротивления зависят от скорости движения осциллятора (например силы сопротивления воздуха):
f тр r rx
где r – коэффициент сопротивления. Тогда второй закон Ньютона запишем в виде:
ma f i
m x kx rx
r
k
2
2 ; 0
m
m
Переобозначим константы.
x 2 x 02 x 0
От случая гармонического осциллятора решение будет отличатся переменной,
зависящей от времени, амплитудой:
x a(t ) cos( t )
Для нахождения значений функции a(t) и значения частоты ω подставим
это решение в исходное уравнение.
x a (t ) cos( t ) a sin( t )
x 2 x 02 x 0
x a (t ) cos( t ) 2a sin( t ) a 2 cos( t )
Проведем простые преобразования:
a cos( t ) 2a sin( t ) a 2 cos( t ) 2 a cos( t ) 2 a sin( t ) 02 a cos( t ) 0
a 2 a a a cos( t ) 2a 2 a sin( t ) 0
a 2 a a( ) cos( t ) 2 a a sin( t ) 0
2
0
2
2
0
2
Такое уравнение равно 0 при любых значениях t, только при условии:
a 2 a a( 02 2 ) 0
a a 0
Из второго уравнения найдем зависимость амплитуды от времени:
da
da
a
dt ln a t C
dt
a
a e t eC при t 0 : a0 eC a a0 e t
Подставим это значение в первое условие и
найдем значение частоты колебаний:
a a; a 2 a
2 a 2 2 a a( 02 2 ) 0
0
2
2
0
2
2
0
2
2
x a0 e t cos[( 02 2 )t ]
T
2
02 2
6

7.

Вынужденные колебания
Вынужденные колебания – колебания, которые возникают в системе
под действием внешней периодической силы.
f F0 cos t
Рассмотрим систему в которой так же присутствует квазиупругая и
диссипативная сила. Тогда второе уравнение Ньютона:
m x kx rx F0 cos t
F0
r
k
;
; 02
m
2m
m
2
x 2 x 0 x f 0 cos t
f0
Колебания описываются неоднородным линейным дифференциальным уравнением
второго порядка. Из теории дифференциальных уравнений известно, что общее решение
такого уравнения может быть найдено, как сумма решений однородного и частного
решения неоднородного уравнения. Решение однородного было найдено ранее:
x a0 e t cos( 1t )
Частное решение неоднородного может быть найдено в виде:
x a cos( t )
Решением этой системы уравнений является функция:
x
2
a0e t cos( 1 )
cos t arctg 2
2
0
( ) 4
f0
2
0
2 2
2
2
Рассмотрим амплитуду вынужденных колебаний:
f0
a
( 02 2 ) 2 4 2 2
Найдем максимальное значение амплитуды – резонансное:
d
( 02 2 ) 2 4 2 2 0
dt
f0
a рез
2
2
2
2
2
4( 0 ) 8 0 0 2
2 02 2 2
max : 0
min : рез 02 2 2
7

8.

Момент инерции
фыва
a cos( 0t )
02 0
02
g
l
0
1
T
1
g
2 2
T
l
g
l
2 ;
M mgl
T 2
1
1
T 2
g
l
l
g
8