Механика привода

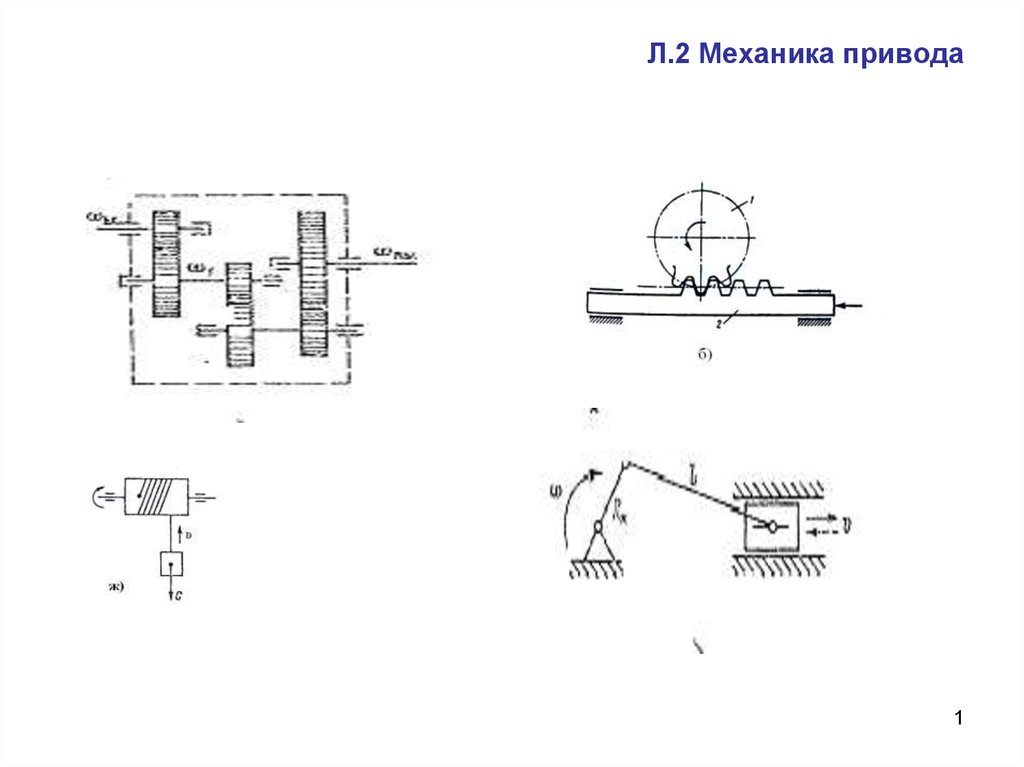
1. Л.2 Механика привода

1

2.

2

3. Л.2 Механика привода

Редуктор
• РЗП
вх
i
вых
V
коэффициент редукции
радиус приведения [ М]
• Шатунно-кривошипный механизм
3

4.

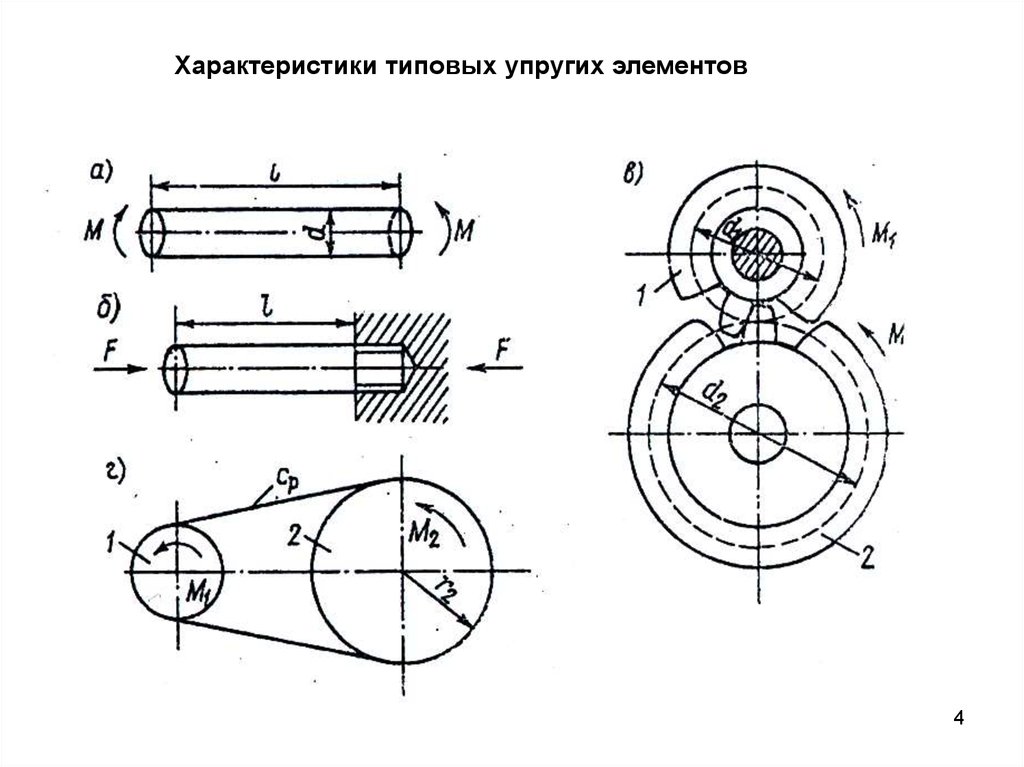
Характеристики типовых упругих элементов
4

5.

Вал, работающий на кручение
характеризуется углом закручивания
Коэффициент жесткости определяется
отношением
М
С
5

6.

Растягиваемый или сжимаемый
стержень,
к которому приложена сила F, имеет следующее
значение жесткости (ньютон на метр)
Ср
F
ES
l
l
- l - линейная деформация стержня,
первого рода, S – площадь стержня.
где
[н/м]
E - модуль упругости
6

7.

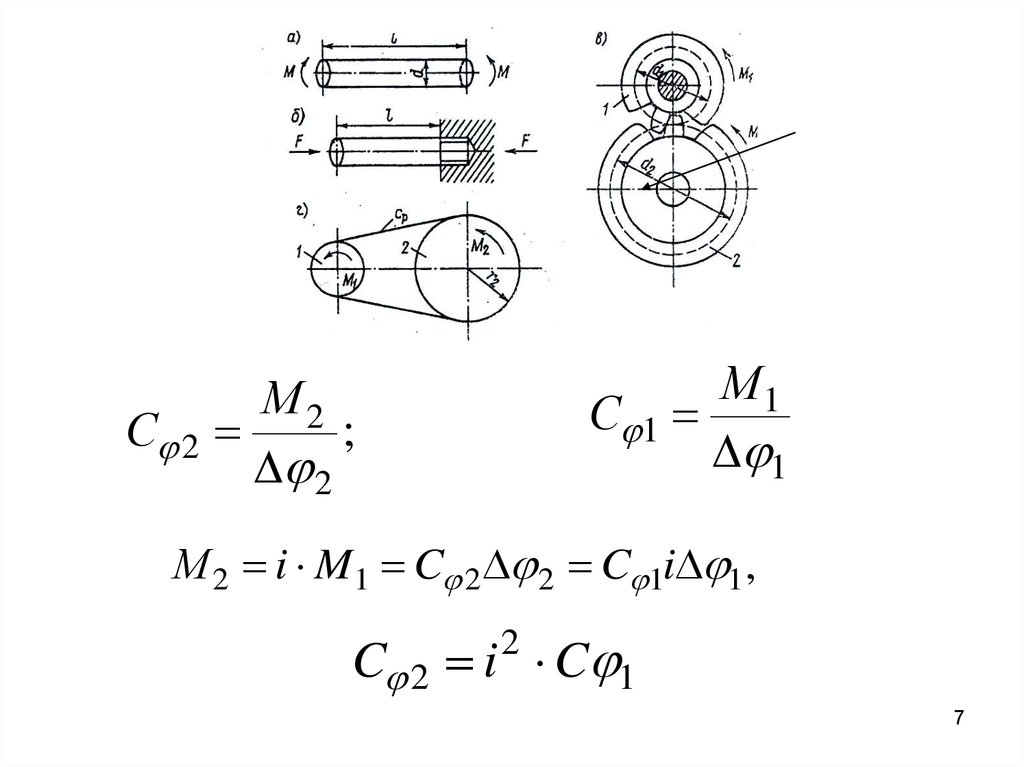
С 2
М1
С 1
1
М2
;
2
М 2 i M1 C 2 2 C 1i 1 ,
C 2 i C 1
2
7

8.

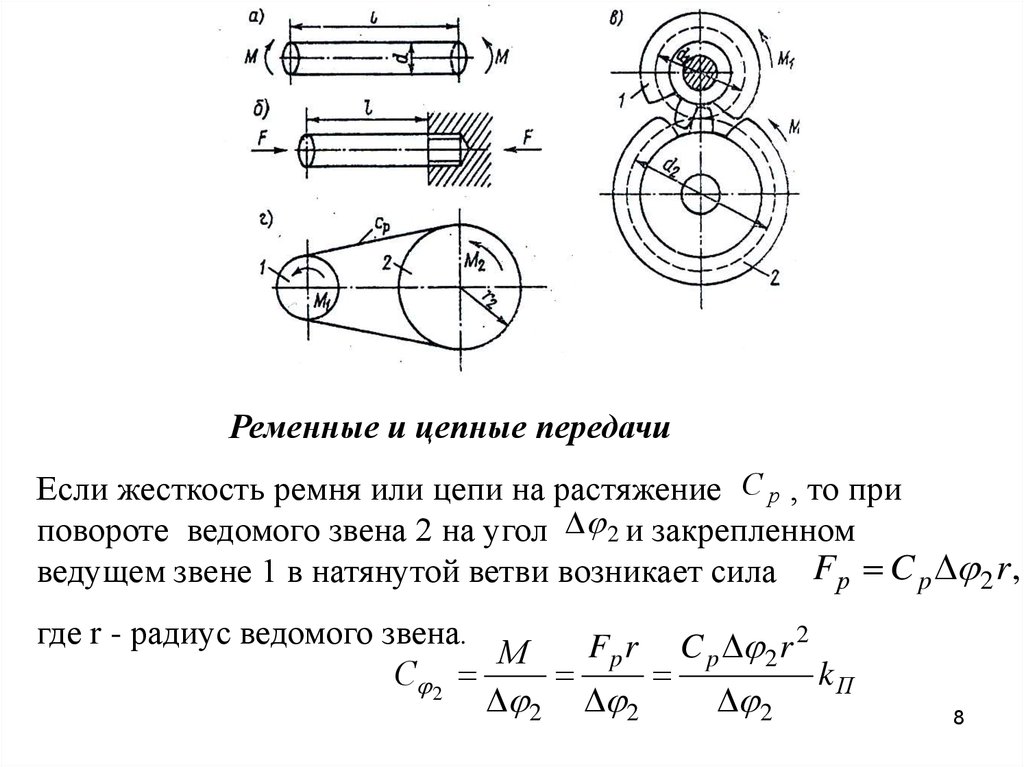
Ременные и цепные передачи
Если жесткость ремня или цепи на растяжение С р , то при
повороте ведомого звена 2 на угол 2 и закрепленном
ведущем звене 1 в натянутой ветви возникает сила Fр C p 2 r ,
2
где r - радиус ведомого звена.
F
r
C
r
М
p
p
2
С 2
kП
2 2
2
8

9.

9

10.

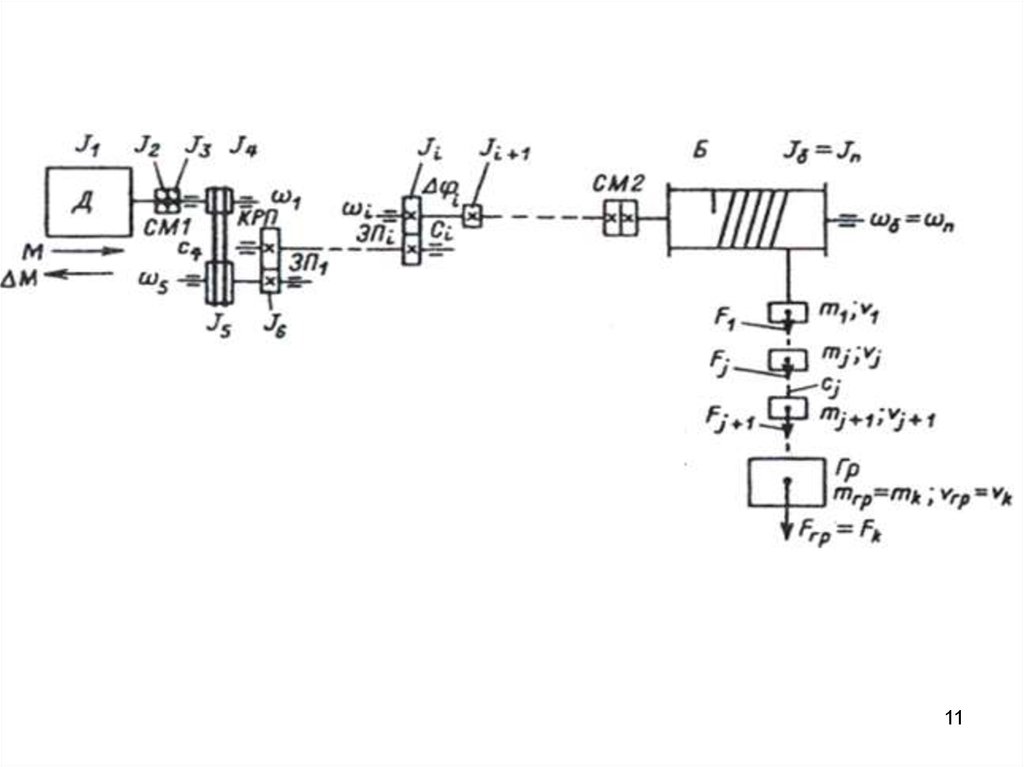
Непосредственное представление о
движущихся массах установки и механических
связях между ними дает кинематическая
схема электропривода.
Конкретные кинематические схемы
отличаются многообразием, однако обладают
и общими свойствами, которые можно
установить с помощью кинематической схемы
электропривода, представленной рисунке.
10

11.

11

12.

Массы элементов и жесткости элементарных
связей в кинематической цепи привода различны.
Определяющее влияние на движение системы
оказывают наибольшие массы и наименьшие
жесткости связей.
Поэтому одной из первых задач проектирования и
исследования электроприводов является
составление упрощенных расчетных схем
механической части, учитывающих возможность
пренебрежения упругостью достаточно жестких
механических связей и приближенного учета
влияния малых движущихся масс. При этом следует
учитывать, что в связи с наличием передач
различные элементы системы движутся с разными
скоростями, поэтому непосредственно сопоставлять
их моменты инерции , массы , жесткости связей и ,
деформации и, перемещения и т.п. невозможно. 12

13.

Для сведения любой реальной системы к
простейшей модели нужно выполнить ряд
операций, называемых приведением моментов и
моментов инерции к некоторому выбранному в
качестве основного валу, обычно - к валу
двигателя.
Иными словами, некоторую реальную
механическую систему, например, показанную на
рисунке, нужно заметить эквивалентной системой ,
такой, чтобы эта замена не отразилась на
поведении части системы, оставленной
неизменной (двигателя).
13

14.

Условием соответствия
приведенной расчетной схемы
реальной механической системе
является выполнение закона
сохранения энергии.
При приведении необходимо обеспечить
сохранение запаса кинетической и
потенциальной энергии системы, а
также элементарной работы всех
действующих в системе сил и моментов
14

15.

При приведении вращательных и поступательных
перемещений необходимо учитывать, что
передаточное число и радиус приведения
определяются соотношением скоростей. Исходя
из этого, в общем случае перемещения в системе
связаны так:
d пр.i d i i1i
d пр. j dS j / 1 j
При линейных кинематических связях i1i const и
1 j const. В этом случае формулы приведения
перемещений имеют вид
пр.i i i1i
пр. j S j / 1 j
15

16.

Приведение моментов и сил нагрузки
элементов кинематической цепи
должно осуществляться на основании
условия равенства элементарной
работы на возможных перемещениях.
Без учета потерь в передачах
М пр.i пр.i М i i ;
M пр.i
Mi
i1i
М пр. j пр. j F j S j .
M пр. j F j 1 j
16

17.

Учет потерь в механической части привода
при прямом направлении передачи энергии и
последовательном соединении нескольких звеньев
кинематической цепи, обладающих потерями
мех 1 2 3 ...,
Мс
М мех
М с 1 М мех мех / мех М 1.
i мех
М
i 1 / i
Потери всегда покрываются той частью системы,
которая создает движение, поэтому при обратном
потоке мощности - от нагрузки к двигателю
М с 1 М мех мех мех М 1.
М мех
Мс
мех М .
i

18.

При приведении момента инерции элемента
системы, движущегося вращательно со
скоростью i или массы, поступательно
движущейся со скоростью V j к расчетной
скорости , должны выполняться условия
J i i2
(Wki ) пр
J пр.i 12
/ 2 Wki
(Wkj ) пр
J пр. j 12
/ 2 Wkj m jV j2
2
/2
J пр.i
Ji
i12i
2
J пр. j m j 1 j
18

19.

• При приведении жесткостей механических
связей должно выполняться условие
равенства запаса потенциальной энергии
деформации упругих элементов.
2
(Wпi ) пр Спр.i пр.i
2
/ 2 Wп.i Ci i
/2
2
2
(Wпj ) пр Спр. j пр
/
2
W
C
s
.j
п. j
j
j /2
Формулы приведения
2
Спр.i Ci / i1i
Спр. j C j / 12j
19

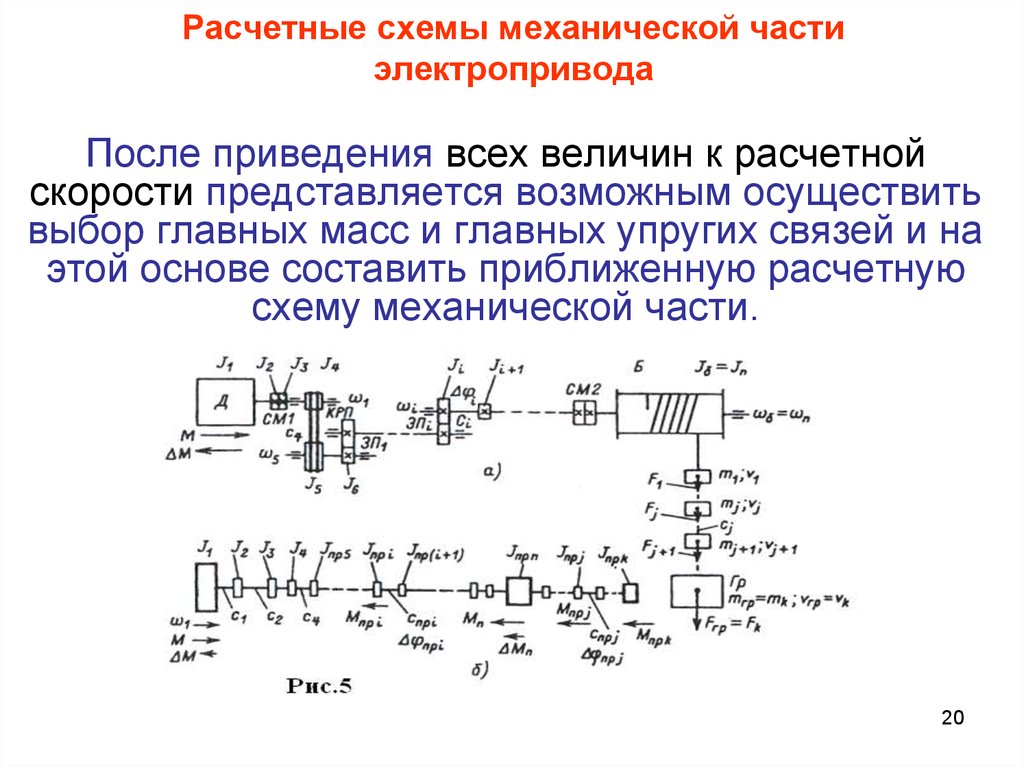
20. Расчетные схемы механической части электропривода

После приведения всех величин к расчетной
скорости представляется возможным осуществить
выбор главных масс и главных упругих связей и на
этой основе составить приближенную расчетную
схему механической части.
20

21. Расчетные схемы механической части электропривода 2

• Для примера в ней выделены три наиболее
значительные массы — ротор двигателя с моментом
инерции J1, барабан с приведенным моментом
инерции Jпр.n и груз Jпр.к. Рассматривая эту схему,
можно видеть, что вследствие малости остальных
моментов инерции ее можно существенно упростить.
Для этого следует малые массы добавить к
близлежащим большим, а затем определить
эквивалентные жесткости связей между
полученными массами по общей формуле
1
1
1
1
....
С экв С1 С 2 С3
21

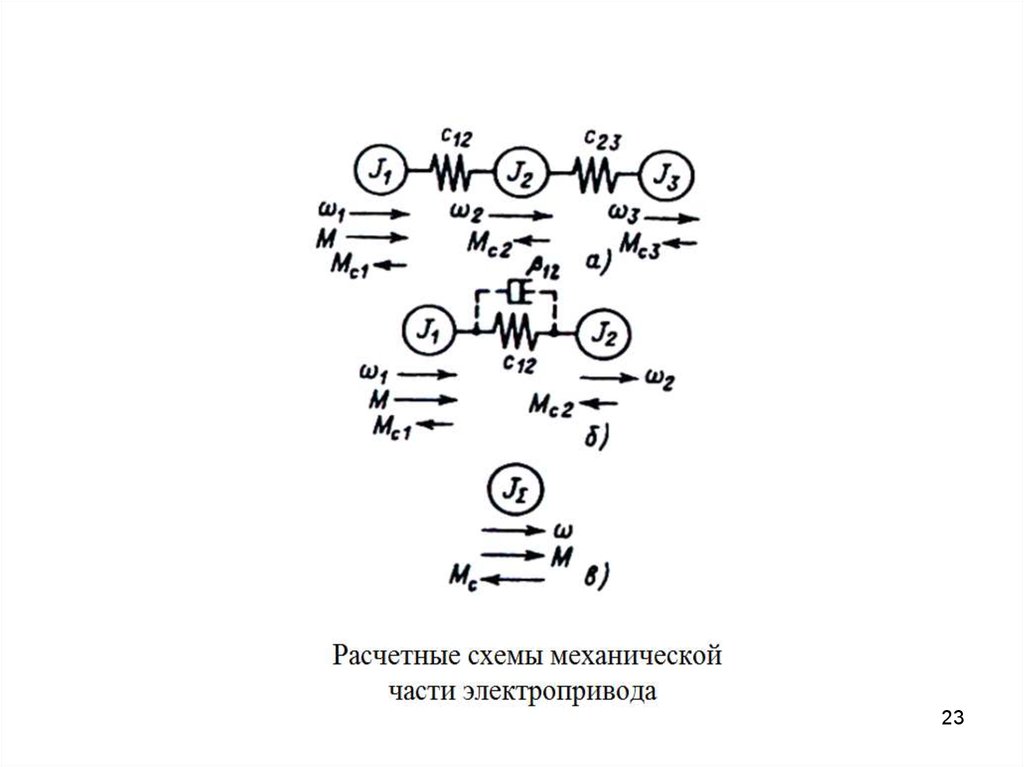
22. Расчетные схемы механической части электропривода

• В большинстве практических случаев в результате
выделения главных масс и жесткостей сводятся к
трехмассовой , двухмассовой расчетным схемам и к
жесткому приведенному механическому звену
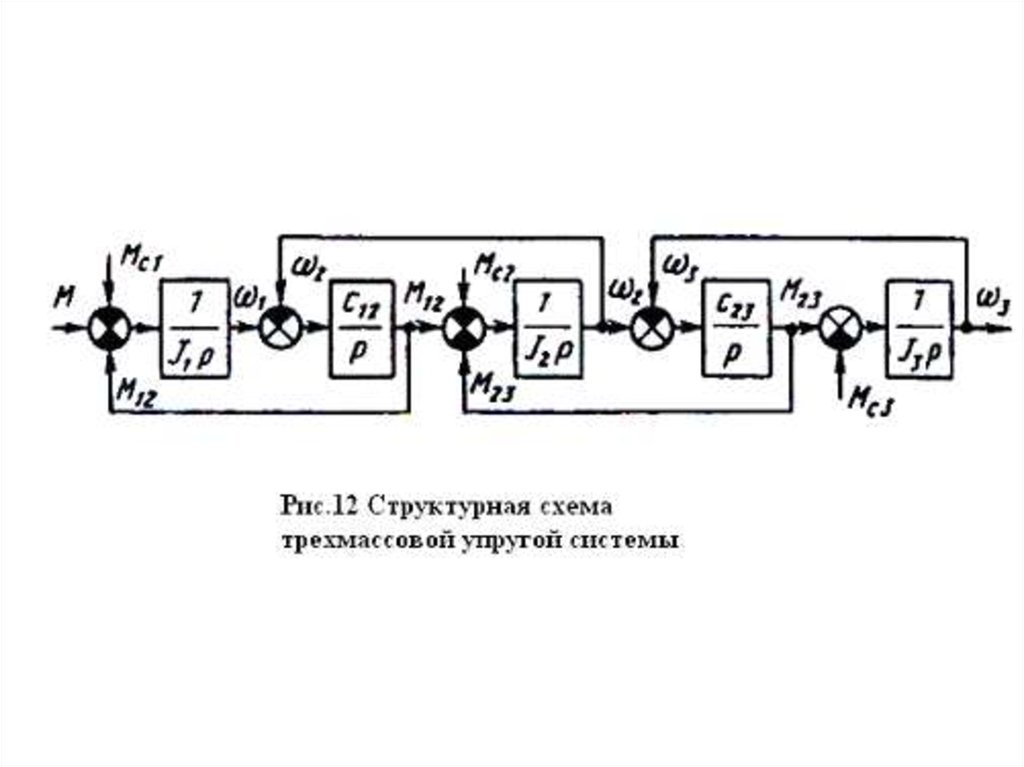
Параметрами обобщенной трехмассовой упругой
механической системы (расчетной схемы) являются
суммарные приведенные моменты инерции J 1 , J 2 ,
J 3 , образованные приведенными массами, связи
между которыми приняты жесткими, и эквивалентные
приведенные жесткости механических упругих связей
между ними
.
22

23.

23

24.

Трехмассовая упругая система
при исследовании электромеханических
систем автоматизированного
электропривода используется в тех
случаях, когда возникает необходимость
более детального анализа условий
движения масс механизма. Для решения
задачи при этом обычно используется
математическое моделирование.
24

25.

Для исследования отдельных физических
особенностей трехмассовая расчетная схема
часто сводится к двухмассовой.
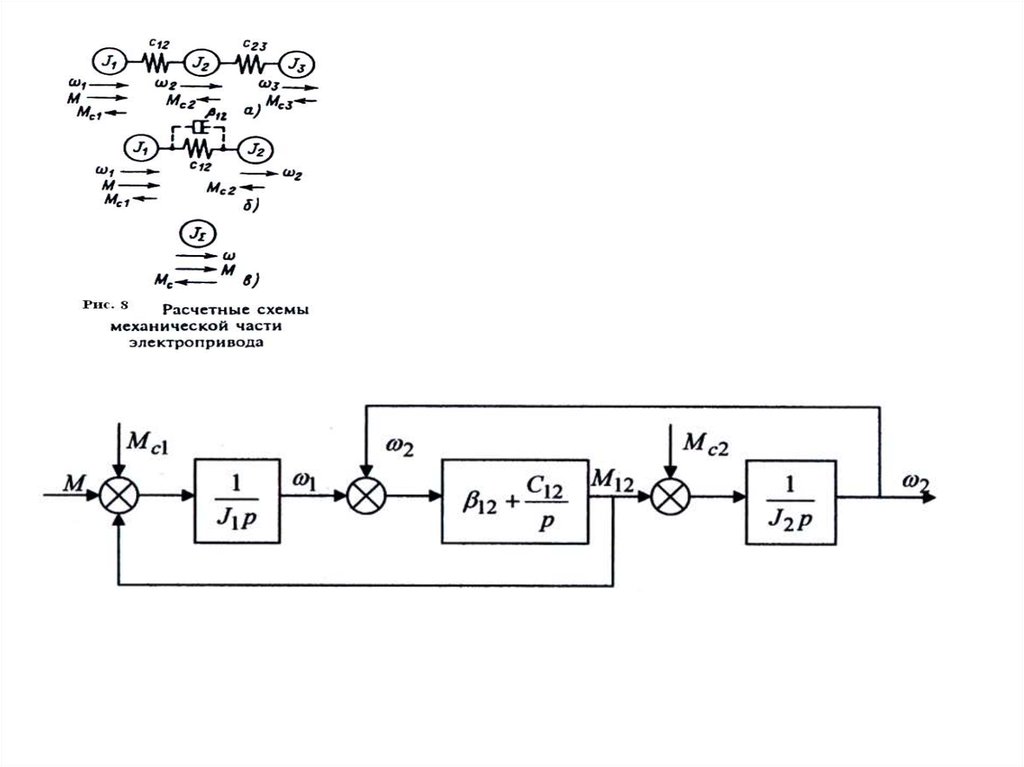
В обобщенной двухмассовой упругой системе
суммарный приведенный момент инерции
элементов, жестко связанных с двигателем,
аналогично предыдущему обозначен J 1 .
Суммарный приведенный момент инерции
элементов, жестко связанных с рабочим органом
механизма, обозначен J 2 . Безынерционная
упругая связь между этими массами
характеризуется приведенной эквивалентной
жесткостью C12 .
25

26.

• Электромеханическая система с
двухмассовой упругой механической
частью представляет собой
простейшую модель
электропривода, наиболее удобную
для изучения влияния упругих
механических связей.
26

27.

В тех случаях когда
влияние упругих связей незначительно, или (при
решении некоторых задач)
с этим влиянием можно не считаться,
механическая часть представляется простейшей
расчетной схемой, не учитывающей влияния упругих
связей, -то есть жестким приведенным звеном.
Расчетная схема представляет собой в этом
случае одну эквивалентную массу, на которую
воздействуют электромагнитный момент двигателя
М и суммарный приведенный к валу двигателя
момент нагрузки . Момент нагрузки включает в себя
все внешние силы, приложенные к механической
системе, кроме момента двигателя М.
27

28.

• Для одномассовой расчетной схемы
суммарный приведенный момент
инерции электропривода может быть
выражен общей формулой
J J дв
i n J
i
2
i
i 2 1i
j k
2
m
j 1j
J 2
• Суммарный приведенный к валу
двигателя момент статической нагрузки
можно в общем виде записать так
i q
Mi
М с
i 1 i1i
j p
F j 1 j
j 1
28

29.

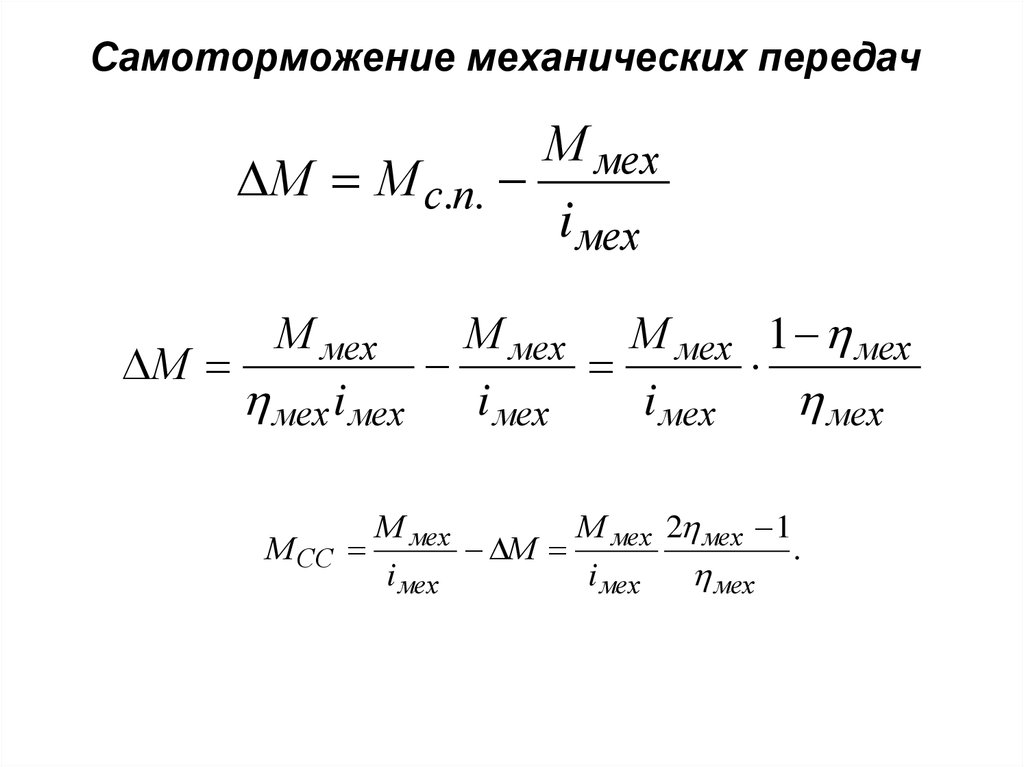
Самоторможение механических передач
М мех
М М с.п.
i мех
М мех
М мех М мех 1 мех
М
мех i мех i мех
i мех
мех
М мех
М мех 2 мех 1
М СС
М
.
i мех
i мех
мех

30.

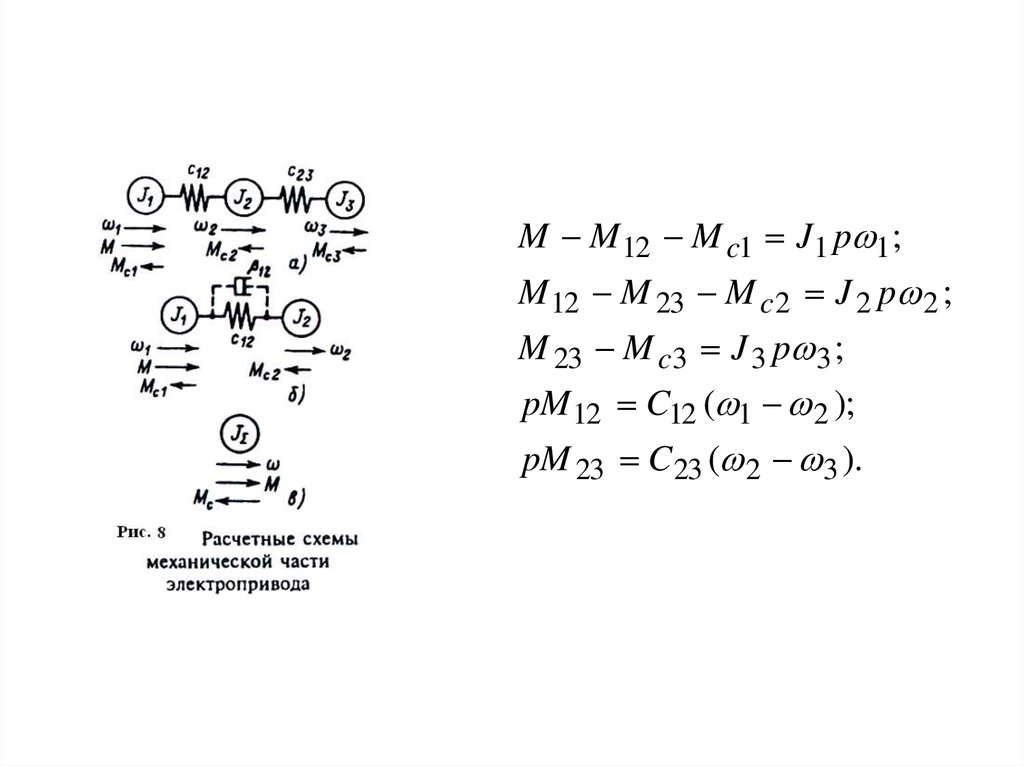
M M 12 M c1 J1 p 1 ;
M 12 M 23 M c 2 J 2 p 2 ;
M 23 M c3 J 3 p 3 ;
pM 12 C12 ( 1 2 );
pM 23 C 23 ( 2 3 ).

31.

32.

1 ( p)
J 2 J 3 p 4 [c23 ( J 2 J 3 ) c12 J 3 ] p 2 c12 c23
W ( p)
M ( P) p{J1 J 2 J 3 p 4 [ J1c23 ( J 2 J 3 )] p 2 c12 c23 ( J1 J 2 J 3 )}
c12 J 3 ( J 1 J 2 ) c 23 J1 ( J 2 J 3 ) 2 c12 c 23 J
p[ p
p
] 0
J1 J 2 J 3
J1 J 2 J 3
4
p1 0,
a
2b
p23 j
(1 1
)
2
2
a
p45 j
a
2b
(1 1
)
2
2
a

33.

34.

J2 2
p 1
c12
W 1 ( p )
J J
J p ( 1 2 p 2 1)
C12 J
J1 J 2 J
J1
J1
12 c12 ( J1 J 2 ) /( J1J 2 )
02 с12 / J 2 12 /
J p(
J1 J 2
c12 J p
2
1) 0
p1 0;
p2,3 j
c12 ( J1 J 2 )
j 12
J1 J 2
резонансная частота системы
резонансная частота второй массы
при жестком закреплении первой

35.

36.

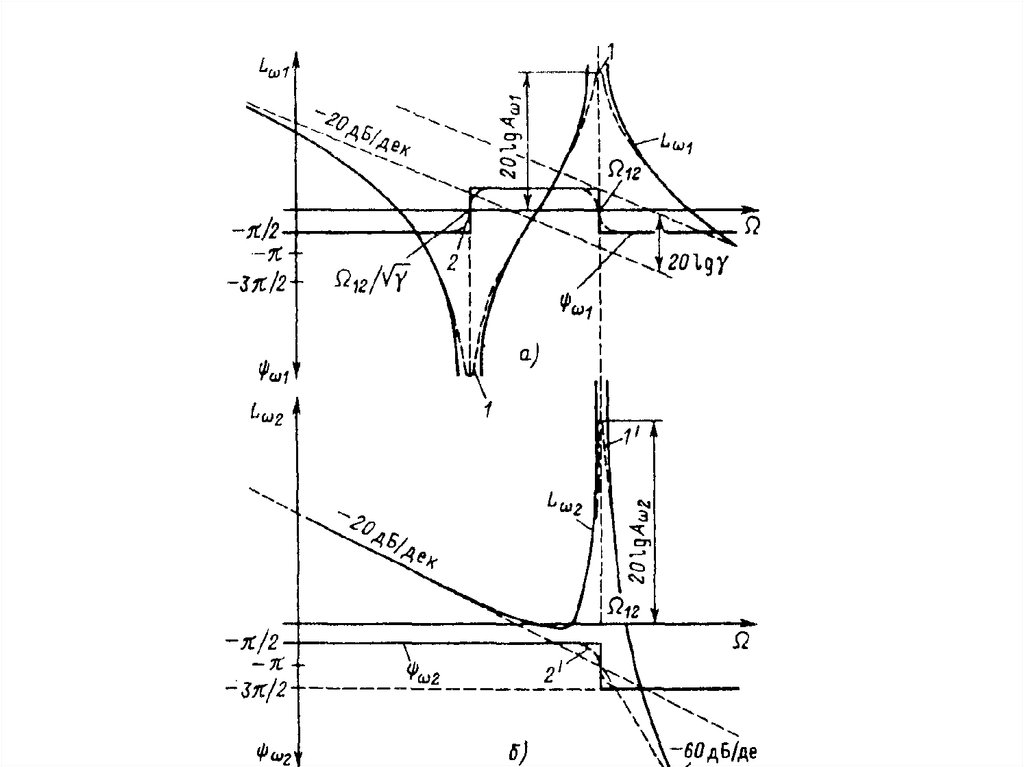
• Обратим внимание на различия во влиянии
упругости на движение первой и второй масс.
Движение первой массы при небольших
частотах колебаний управляющего
воздействия М определяется суммарным
моментом инерции электропривода , причем
механическая часть ведет себя как
интегрирующее звено.

37.

При приближении частоты колебаний
момента к резонансной амплитуды
колебаний скорости возрастают и при
12 стремятся к бесконечности. Однако
проявления резонанса существенно зависят
от параметров механической части в связи с
наличием в числителе передаточной
функции форсирующего звена второго
порядка.

38.

Если механизм обладает небольшой инерцией (J2 много меньше
чем J1) то движение первой массы близко к движению,
определяемому интегрирующим звеном
WИ 1 / J p
При 12
в области малых и средних частот движение
первой массы определяется тем же интегрирующим звеном.
Отсюда вытекает важный практический вывод.
Если при синтезе электропривода используются
обратные связи только по переменным двигателя, то при
J 2 J1 , или 12 c , где c частота среза
желаемой ЛАЧХ разомкнутого контура электропривода,
можно представить жестким механическим звеном, не
учитывая влияния упругостей.

39.

C
1
( 12 12 )
( p)
J2 p
p J1 p
W / ( p ) 1
1
C12 1
C12 1
M ( p)
1 ( 12
)
( 12
)
p J1 p
p J2 p
1
12
C12
p
2
2 в.т. р 12
1
2
2
J1 J 2 p ( J1 J 2 )( 12 p C12 ) J1 J 2 р ( р 2 2 в.т. р 12
2 в.т.
12 ( J1 J 2 )
J1 J 2
2
р 2,3 в.т. j 12
в2.т.
J1 J 2
2
C12
12
J1 J 2
/
2
12
12
в2.т.

40.

Когда параметры системы таковы, что влияние упругих
связей незначительно, или при решении задач, в которых с
этим влиянием можно не считаться, механическая часть
представляется простейшей расчетной схемой, не
учитывающей влияния упругих связей, - жестким
приведенным звеном
J J дв
i n J
i
2
i 2 i1i
j k
m j 12j
J 2
i q
Mi
М с
i 1 i1i
j p
F j 1 j
j 1
d
М Мс J
dt
40

41.

41

42.

Для устойчивости статического
режима необходимо, чтобы при
бесконечно малом отклонении скорости
d , вызванном каким либо
возмущением, система стремилась в
исходное состояние. Последнее
означает необходимость возникновения
в окрестности точки статического
равновесия с d бесконечно малого
приращения динамического момента
dM дин , имеющего знак,
противоположный знаку d .

43.

M ( , t ) M c ( ) J
d
dt
d [ M ( , t ) M c ( )] sign (d ) dM Д
M c
M
M
d
dt _
d sign (d ) dM Д
d
t d
d
c
c
c
M c
M
d
d sign (d ) dM Д .
d
d
c
c

44.

{
M c
M
}d sign (d ) dM Д
d
d
c
c
M c
M
0
d
d
c
c
Д
с
d
c. мех
с
d
‹ 0.

45.

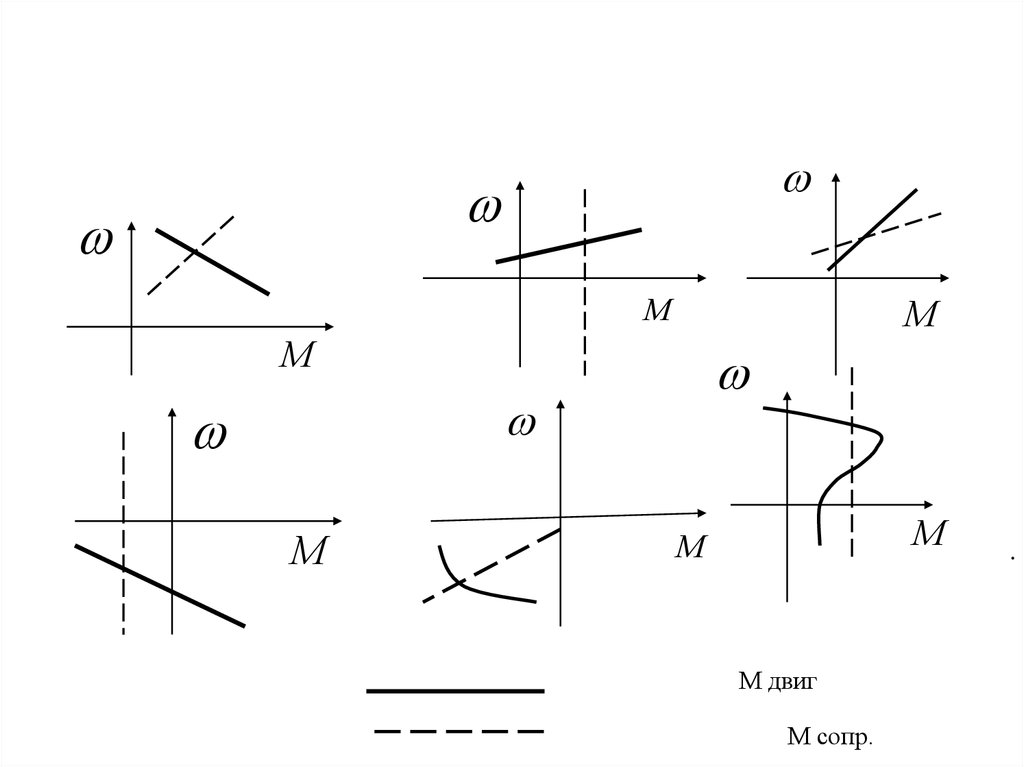
М
М
М
М
М
М
М двиг
М сопр.
.

46.

Материал лекции 2
(Л1-стр.22-40, Л3 - гл.2, Л4 – стр. 24-60)
46