Lek2_AFK

1. Тема 2

Элементы
аналитической
геометрии

2. §1. Уравнение линии на плоскости

Линии на плоскости рассматриваются как
геометрические места точек, их составляющих.
Введение на плоскости системы координат
позволяет
положение
точек
плоскости
однозначно
определять
заданием
пар
действительных чисел – их координат, а
положение линий на плоскости определять с
помощью равенств, связывающих пары чисел –
координаты точек этих линий, то есть с помощью
уравнений.

3.

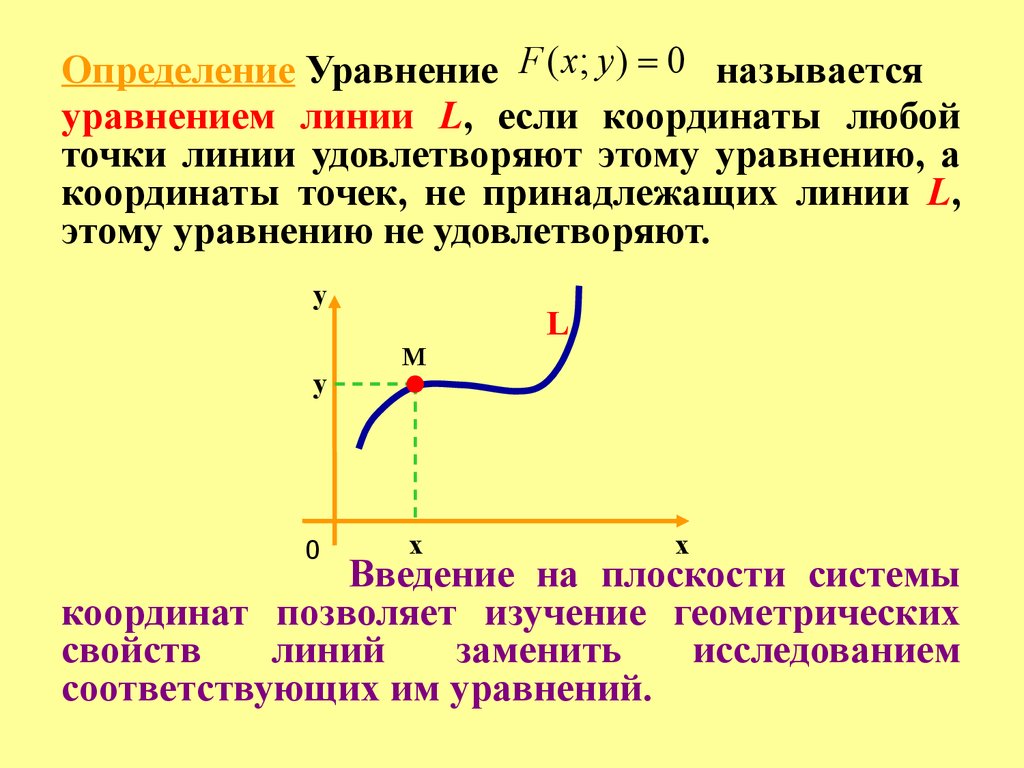
Определение Уравнение F ( x; y ) 0 называется
уравнением линии L, если координаты любой
точки линии удовлетворяют этому уравнению, а
координаты точек, не принадлежащих линии L,
этому уравнению не удовлетворяют.
y
y
0
L
М
x
x
Введение на плоскости системы
координат позволяет изучение геометрических
свойств
линий
заменить
исследованием
соответствующих им уравнений.

4. §2. Прямая линия. Различные уравнения прямой

2.1. Уравнение прямой, проходящей через данную точку,
параллельно данному вектору
Проведем прямую через данную точку М 0 ( x0 ; y0 ),
параллельно данному вектору а l ; m .
а
М 0 ( x0 ; y0 )
М ( x; y )
Возьмем на прямой произвольную точку М ( x; y ) , тогда
векторы а и М 0 М - коллинеарны и их координаты
пропорциональны. Так как
М 0 М x x0 ; y y0
x x0 y y0
l
m
а l ; m
, то получим:
- уравнение прямой, проходящей через
данную точку, параллельно данному
вектору

5.

2.2. Уравнение прямой, проходящей через две данные
точки
Проведем прямую через две данные точки М 1 ( x1 ; y1 )
и М 2 ( x2 ; y 2 ) .
М 2 ( x2 ; y 2 )
М ( x; y )
М 1 ( x1 ; y1 )
Возьмем произвольную точку М ( x; y ) на прямой, тогда
векторы М 1М и М 1М 2- коллинеарны и их координаты
пропорциональны.
Так как М М x x ; y y ,
1
1
1
М 1М 2 x2 x1 ; y2 y1 , то получим:
x x1
y y1
x2 x1 y2 y1
- уравнение прямой, проходящей через
две данные точки

6.

2.3. Уравнение прямой в отрезках
Пусть прямая отсекает на осях координат соответственно
отрезки а и b. Можно считать, что прямая проходит через
две данные точки М 1 (а ; 0 )и М 2 ( 0; b )и по пункту 2.2.
имеем:
x x1 y y1
x2 x1 y2 y1
y
М 2 (0; b)
b
М 1 (а;0)
0
а
x y
1
a b
x
x a y 0
0 a b 0
x a y
a a b
x
y
1
a
b
- уравнение прямой в отрезках

7.

2.4. Уравнение прямой с угловым коэффициентом
Рассмотрим уравнение прямой из пункта 2.1.:
y
x x0 y y 0
l
m
( x x0 ) m ( y y 0 ) l
а l ; m
m
l
0
y y0 k ( x x0 )
x
m
y y 0 ( x x0 )
l
m
Обозначим
k
l
m
tg )
(так как
l
- уравнение прямой, проходящей
через данную точку с угловым
коэффициентом k

8.

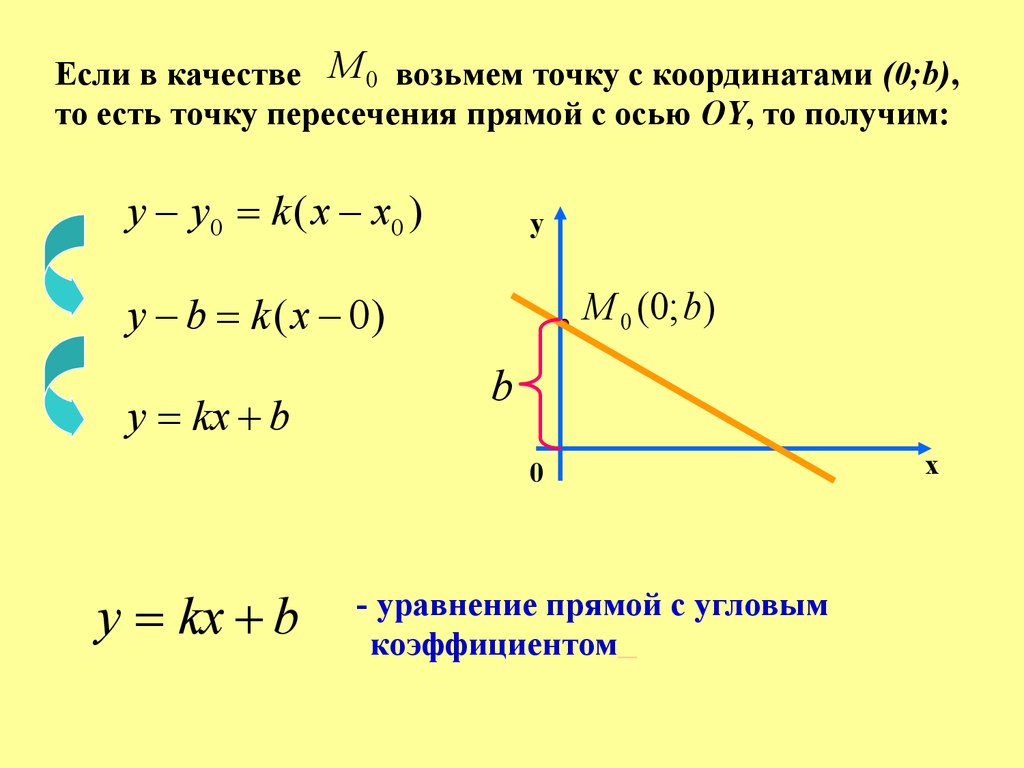
Если в качестве М 0 возьмем точку с координатами (0;b),
то есть точку пересечения прямой с осью OY, то получим:
y y0 k ( x x0 )
y
М 0 (0; b)
y b k ( x 0)
y kx b
b
0
y kx b
- уравнение прямой с угловым
коэффициентом
x

9.

2.5. Уравнение прямой, проходящей через данную точку
перпендикулярно данному вектору
Проведем прямую через данную точку М 0 ( x0 ; y0 )
перпендикулярно данному вектору N A; B . Возьмем на
прямой произвольную точку М ( x; y )и рассмотрим вектор
М 0 М x x0 ; y. y0
N A; B
М ( x; y )
М 0 ( x0 ; y0 )
Вектор М 0 М и N взаимно перпендикулярны ( М 0 М N )
и по условию перпендикулярности векторов М М N 0
0
получим:
- уравнение прямой,
( x x0 ) A ( y y0 ) B 0
проходящей через данную
точку перпендикулярно
данному вектору

10.

2.6. Общее уравнение прямой
Рассмотрим предыдущее уравнение и раскроем
скобки:
( x x0 ) A ( y y0 ) B 0
Ax By ( Ax0 By 0 ) 0
Обозначим ( Ax0 By 0 ) С, получим:
Ax By C 0
- общее уравнение прямой
Замечание При решении задач на составление уравнений
прямых ответ принято записывать в виде общего
уравнения или уравнения с угловым коэффициентом.

11. §3. Взаимное расположение прямых

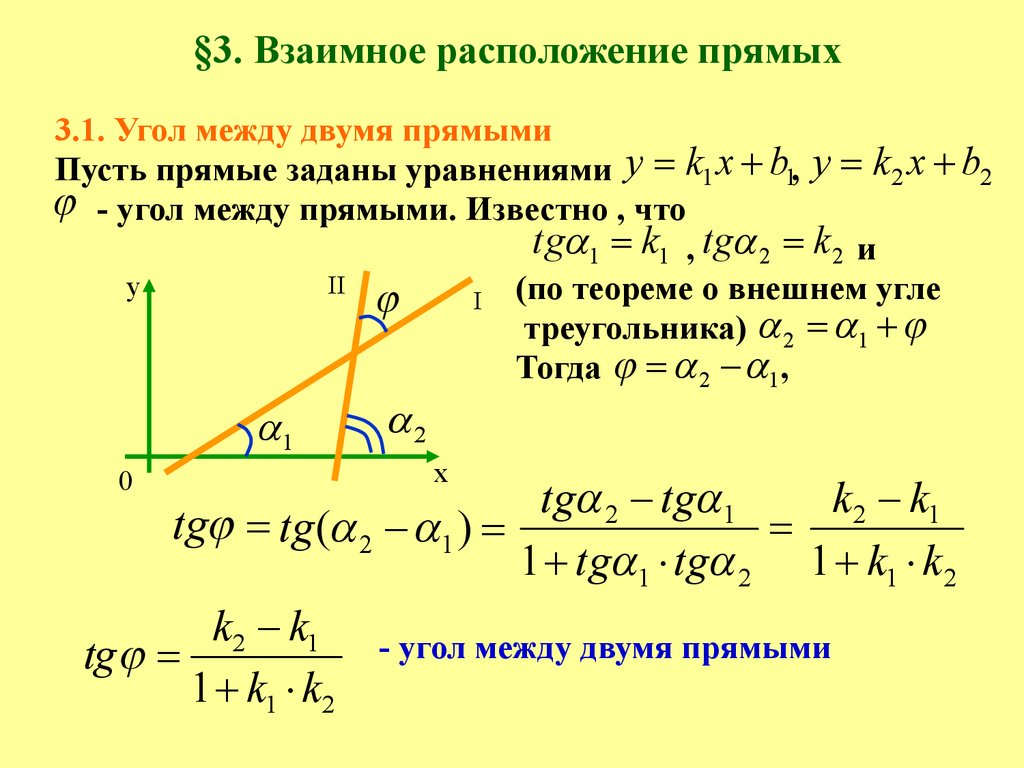
3.1. Угол между двумя прямыми
Пусть прямые заданы уравнениями y k1 x b1, y k 2 x b2
- угол между прямыми. Известно , что
tg 1 k1 , tg 2 k 2 и
II
y
I (по теореме о внешнем угле
треугольника) 2 1
Тогда 2 1,
1
0
2
x
tg 2 tg 1
k 2 k1
tg tg ( 2 1 )
1 tg 1 tg 2 1 k1 k 2
k 2 k1 - угол между двумя прямыми
tg
1 k1 k 2

12.

3.2. Условие параллельности прямых
Если прямые параллельны, то 1 2 и tg 1 tg 2
или k1 k 2 .
y
I
1
0
k1 k 2
II
2
x
- условие параллельности двух прямых

13.

3.3. Условие перпендикулярности прямых
0
90
Если0 прямые перпендикулярны, то
.
tg 90 не существует, а это случится тогда, когда
1 k1 k 2 0
y
II
0
k1 k 2 1
k 2 k1
tg
1 k1 k 2
I
x
k1 kили
2 1
- условие перпендикулярности
двух прямых

14.

Замечание Если прямые заданы общими уравнениями
A x B y C 0 , A x B y C 0 , то
1
1
А1 В1
А2 В2
1
2
2
2
- условие параллельности двух прямых
A1 А2 B1 В2 0
- условие перпендикулярности
двух прямых

15. §4. Расстояние от точки до прямой

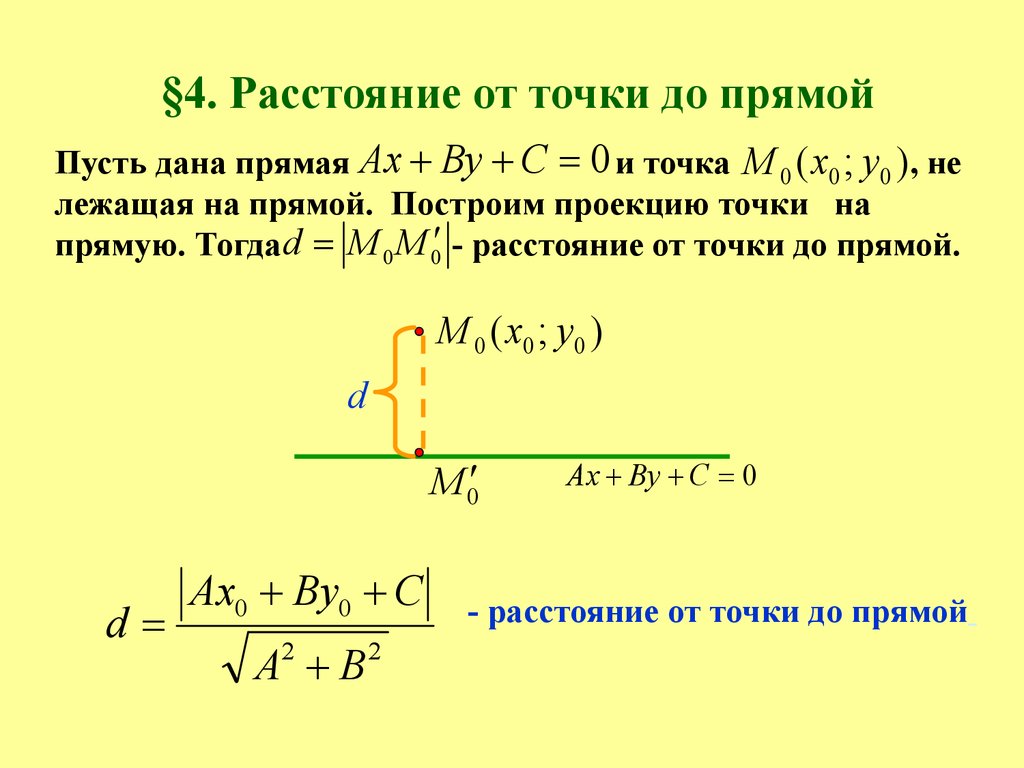
Пусть дана прямая Ax By C 0 и точка М 0 ( x0 ; y0 ), не
лежащая на прямой. Построим проекцию точки на
прямую. Тогда d M 0 M 0 - расстояние от точки до прямой.
М 0 ( x0 ; y0 )
d
М 0
d
Ax0 By0 C
A B
2
2
Ax By C 0
- расстояние от точки до прямой

16. §5. Кривые второго порядка

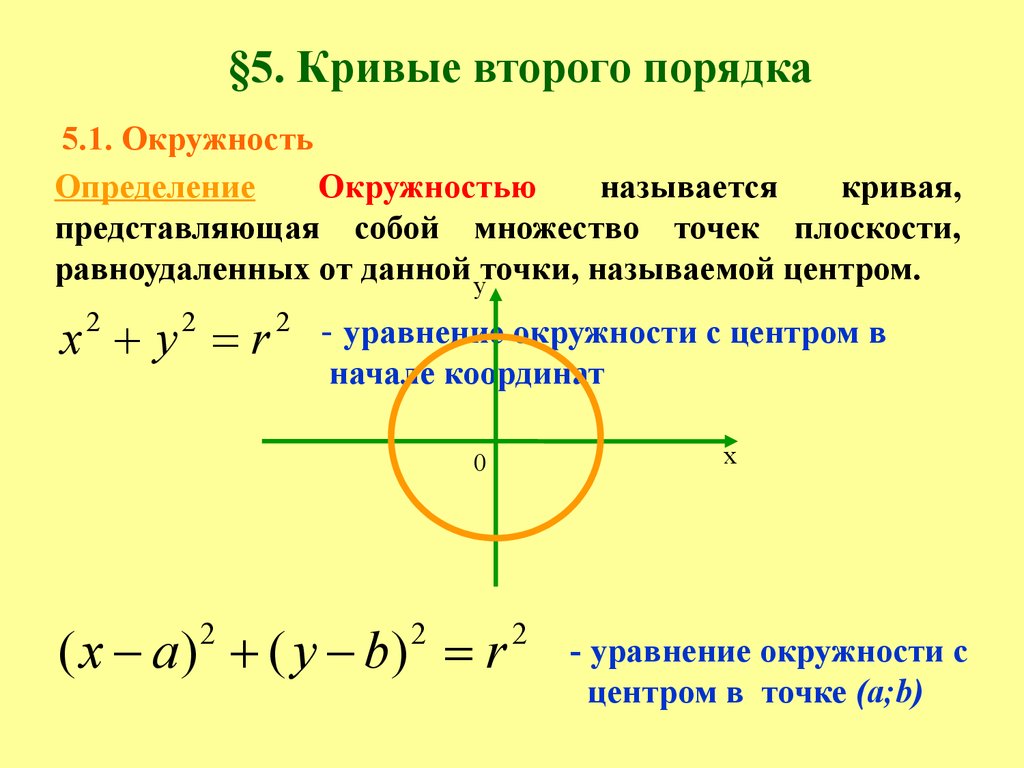
5.1. Окружность
Определение
Окружностью
называется
кривая,
представляющая собой множество точек плоскости,
равноудаленных от данной yточки, называемой центром.
x y r
2
2
2
уравнение окружности с центром в
начале координат
-
x
0
( x a ) ( y b) r
2
2
2
- уравнение окружности с
центром в точке (а;b)

17.

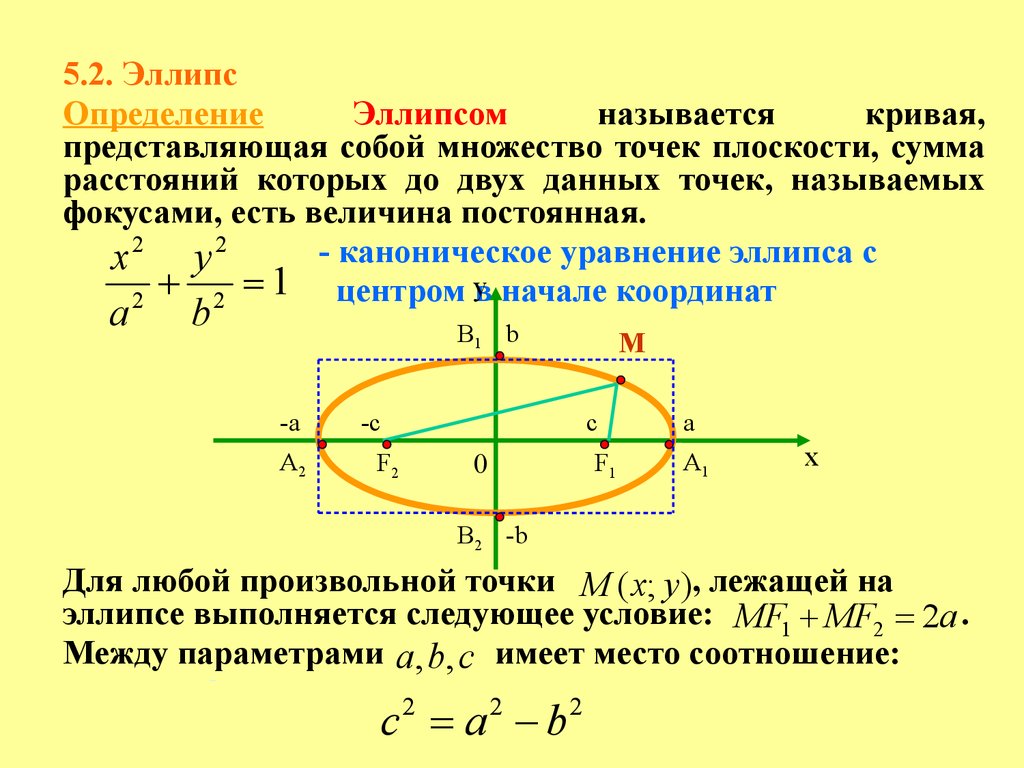
5.2. Эллипс
Определение
Эллипсом
называется
кривая,
представляющая собой множество точек плоскости, сумма
расстояний которых до двух данных точек, называемых
фокусами, есть величина постоянная.
- каноническое уравнение эллипса с
x2 y2
2 1 центром yв начале координат
2
a
b
В1 b
-a
А2
М
-с
с
0
F2
F1
a
А1
x
В2 -b
Для любой произвольной точки М ( x; y ), лежащей на
эллипсе выполняется следующее условие: MF1 MF2 2а .
Между параметрами a, b, c имеет место соотношение:
c a b
2
2
2

18.

Свойства эллипса
1. Эллипс симметричен относительно осей координат.
2. Эллипс имеет два фокуса F1 (c;0) , F2 ( c;0) и четыре
вершины A1 (a;0), A2 ( a;0), B1 (0; b) , B2 (0; b).
3. Эллипс имеет две оси: A1 A2 - большая ось, В1В2 - малая ось.
A1 A2 2a . В1 В2 2b .
с
4.Степень сжатости эллипса определяет число
,
а
называемое эксцентриситетом.
5. Четырехугольник, проходящий через точки A1 , A2 , В1 , В2 со
сторонами, параллельными осям координат, называется
характеристическим.

19.

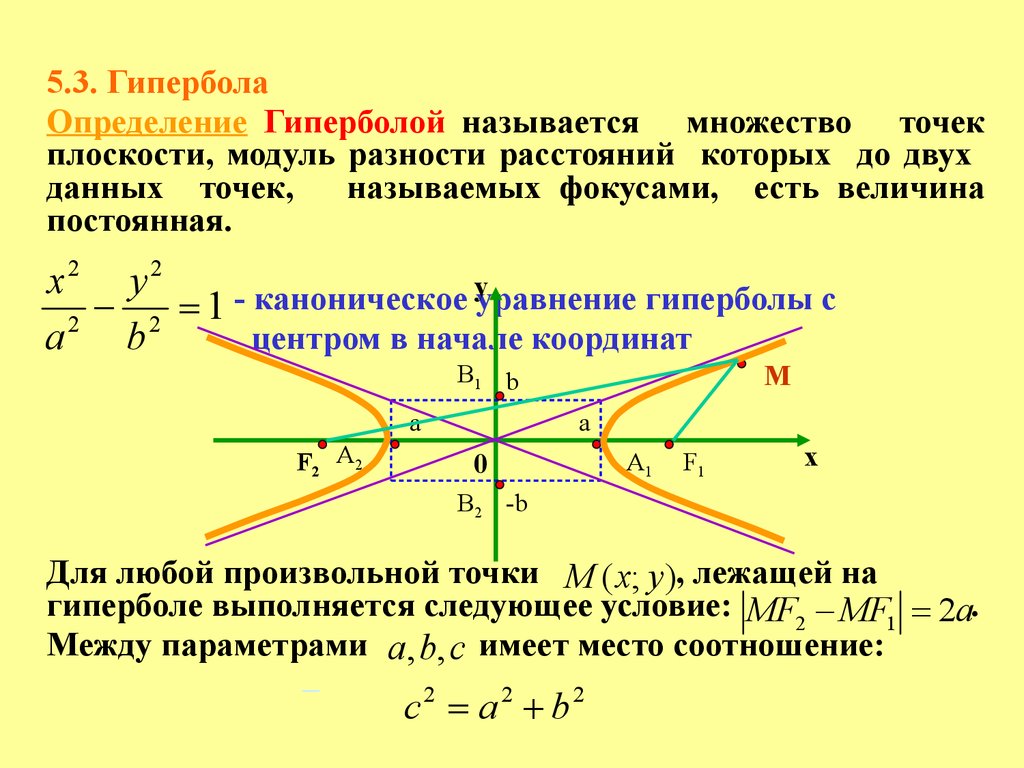
5.3. Гипербола
Определение Гиперболой называется множество точек
плоскости, модуль разности расстояний которых до двух
данных точек,
называемых фокусами, есть величина
постоянная.
x2 y2
yуравнение гиперболы с
каноническое
2 1
2
центром в начале координат
a
b
В1 b
-a
F2 А2
М
a
0
А1
F1
x
В2 -b
Для любой произвольной точки М ( x; y ), лежащей на
гиперболе выполняется следующее условие: MF2 MF1 2а.
Между параметрами a, b, c имеет место соотношение:
c2 a2 b2

20.

Свойства гиперболы
1. Гипербола симметрична относительно осей координат.
2. Гипербола имеет два фокуса F1 (c;0) , F2 ( c;0) и две
вершины A1 (a;0) , A2 ( a;0) .
3. Гипербола имеет две оси: A1 A2 - действительная ось,
В1В2 - мнимая ось. A1 A2 2a . В1 В2 2b .
с
4.Степень сжатости гиперболы определяет число ,
а
называемое эксцентриситетом.
5.Четырехугольник, проходящий через точки A1 , A2 , В1 , В2
со сторонами, параллельными осям координат,
называется характеристическим. Его диагонали
являются
асимптотами
гиперболы.
Уравнения
асимптот:
b
b
y x и y x .
a
a

21.

5.4. Парабола
Определение Параболой называется множество точек на
плоскости, равноудаленных от данной точки, называемой
фокусом, и от данной прямой, называемой директрисой.
y 2 px
2
- каноническое уравнение параболы с
вершиной
в начале координат
y
K
М
Обозначим расстояние от фокуса до директрисы p , тогда
p
x – уравнение директрисы.
2
p до директрисы
x
0
F делится точкой
Расстояние от фокуса
2
начала координат пополам.
Для любой произвольной точки М ( x; y ) , лежащей на
параболе выполняется следующее условие: MK MF .

22.

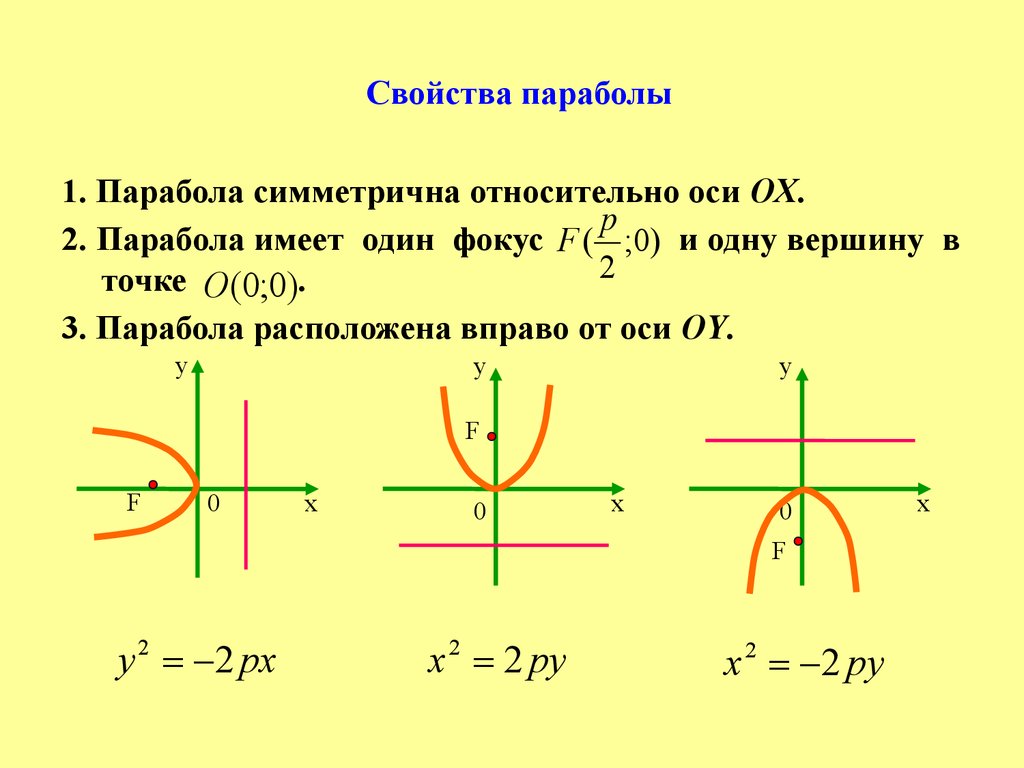
Свойства параболы
1. Парабола симметрична относительно оси OX.
p
2. Парабола имеет один фокус F ( ;0) и одну вершину в
2
точке О (0;0).
3. Парабола расположена вправо от оси OY.
y
y
y
F
F
0
x
0
x
0
F
y 2 2 px
x 2 2 py
x 2 2 py
x

23. §6 Векторы в пространстве

В пространстве, как и на плоскости, вектором
называется направленный отрезок.
Так же определяются основные понятия для
векторов в пространстве: модуль вектора, равные
вектора.
Определение Векторы называются компланарными,
если существует плоскость, которой они параллельны.
Три вектора, среди которых имеется хотя бы
один нулевой вектор, считаются компланарными.

24.

6.1.Координаты вектора в пространстве
Введем в пространстве прямоугольную систему
координат XOYZ. Возьмем произвольный вектор а .
прox a x
прoy a y
прoz a z
Записывают
- координаты вектора
а x; y; z
Если А(x1;y1;z1), B(x2;y2;z2), то
а АВ x2 x1 ; y2 y1 ; z2 z1

25.

6.2. Разложение вектора по ортам
Векторы i , j , k удовлетворяющие следующим условиям:
1. начало
каждого
из
них лежит в начале координат;
2. i 1, j 1 , k 1;
3. вектор i направлен по направлению оси OX,
j направлен по оси OY,
k направлен по оси OZ,
называются ортами или прямоугольным базисом
a x i y j z k
(i; j; k ) .
- разложение вектора апо
ортам, где а x; y; z

26.

6.3. Задача деления отрезка в данном отношении
Пусть А(x1;y1;z1), B(x2;y2;z2) и отрезок АВ разделен точкой
М(x;y;z) в отношении АМ : MB , то координаты
точки М находят по формулам:
x1 x2
x
1
y1 y2
z1 z 2
y
z
1
1

27.

6.4. Длина вектора
Пусть
а x; y; z
, тогда
2
2
2
а x y z
6.5. Действия над векторами в координатной форме
Пусть a x1 ; y1 ; z1 , b x ; y ; z , тогда
2
2
2
1. a b x x ; y y ; z z
1
2
1
2 1
2
2. a x ; y ; z
1
1
1
3. Если
, то x x , y y , z z .
a b
1
2
1
2
1
2

28.

6.6. Условие коллинеарности двух векторов
Если
a x1; y1 ; z1 и b x2 ; y2 ; z 2 - коллинеарны, то
x1
y1
z1
x2
y2
z2
и наоборот.
6.7. Скалярное произведение векторов в координатной
форме
Если
a x1; y1 ; z1 и b x2 ; y2 ; z 2 , то
a b x1 x2 y1 y2 z1 z 2

29.

Следствия из свойств скалярного произведения в
координатной форме
1. cos( a ; b )
2.
x1 x2 y1 y2 z1 z 2
2
2
2
2
2
x1 y1 z1 x2 y2 z 2
x
x
y
y
z
z
1
2
1
2
1
2
прb a
2
2
2
x2 y 2 z 2
2

30.

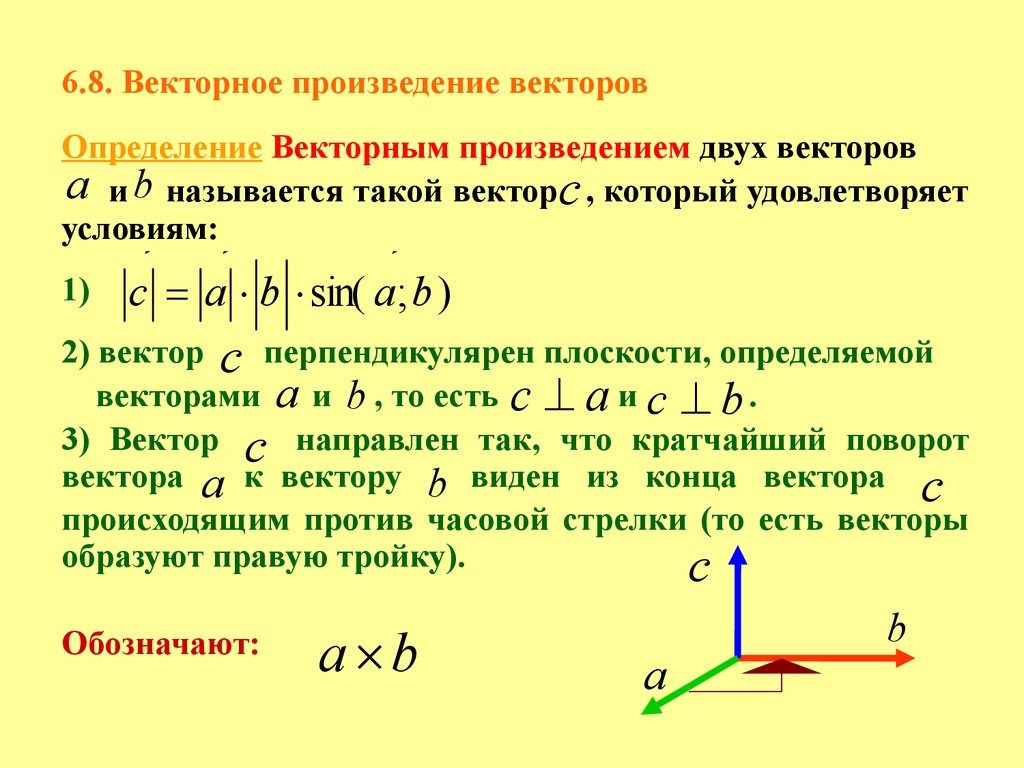
6.8. Векторное произведение векторов
Определение
Векторным произведением
двух векторов
а и b называется такой векторс , который удовлетворяет
условиям:
1)
с а b sin( a; b )
2) вектор с перпендикулярен
плоскости,
определяемой
векторами а и b , то есть с а и с b .
3) Вектор с направлен
так, что кратчайший поворот
вектора а к вектору b виден из конца вектора с
происходящим против часовой стрелки (то есть векторы
образуют правую тройку).
с
Обозначают:
а b
а
b

31.

Модуль векторного произведения равен
площади
параллелограмма S, построенного на векторах
а и b, то есть
a b S
Если a x ; y ; z , b x ; y ; z , то
1
1 1
2
2
2
i j k
y1 z1 x z1 x1 y
1
a b x1 y1 z1
i 1
j
k
y2 z2
x2 z 2
x2 y2
x2 y 2 z 2
( y1 z 2 z1 y2 ) i ( z 2 x1 x2 z1 ) j ( x1 y2 y1 x2 ) k

32.

6.9. Направляющие косинусы векторов
Определение Косинусы углов, образуемых радиус
вектором а с координатными осями OX,
OY, OZ, называются
направляющими косинусами вектора а.
x
cos
a
x
x2 y2 z 2
z
cos
a
y
cos
a
z
x2 y2 z 2
cos 2 cos 2 cos 2 1
y
x2 y2 z 2

33. §7. Плоскости в пространстве

7.1. Уравнение плоскости в пространстве
; z0 ) - точка,
Пусть P – плоскость, М 0 ( x0 ; y0
принадлежащая этой плоскости, а n A; B; C - ненулевой
вектор,
перпендикулярный
плоскости
Р,
который
называется нормальным вектором плоскости.
М ( x; y; z ) - произвольная точка на плоскости Р.
z
r0
k
i
j
x
М0 М
r
n
Р
n (r r0 ) 0 - уравнение
плоскости в
векторной форме
A( x x0 ) B ( y y0 ) C ( z z0 ) 0
- уравнение плоскости, проходящей
через данную точку в заданном
y
направлении
Ax By Cz D 0 - общее уравнение плоскости

34.

7.2. Угол между двумя плоскостями
Угол между двумя плоскостями равен углу между их
нормальными векторами.
Пусть две пересекающиеся плоскости
A1 x B1 y C1 z D1 0 и A2 x B2 y C2 z D2 0
имеют нормальные векторы
n2 A2 ; B2 ; C2
n1 A1; B1 ; C1
и
Тогда угол между этими плоскостями вычисляется по
формуле:
n1 n2
cos
n1 n2
A1 A2 B1 B2 C1 C2
2
2
2
2
2
A1 B1 C1 A2 B2 C2
2

35.

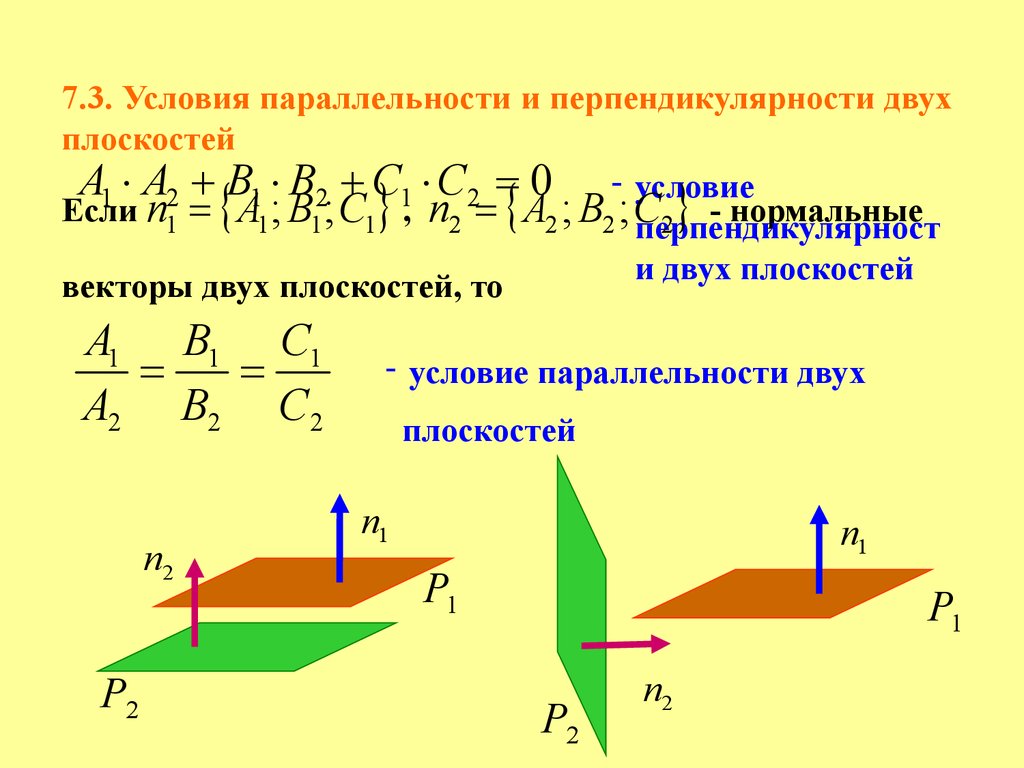
7.3. Условия параллельности и перпендикулярности двух
плоскостей
A1 A 2 B1 B2 C1 C2 0 - условие
Если n1 A1 ; B1 ; C1 , n2 A2 ; B2 ; C
2 - нормальные
перпендикулярност
и двух плоскостей
векторы двух плоскостей, то
A1 B1 C1
A2 B2 C2
n2
Р2
- условие параллельности двух
плоскостей
n1
n1
Р1
Р1
Р2
n2

36. §8. Прямая в пространстве

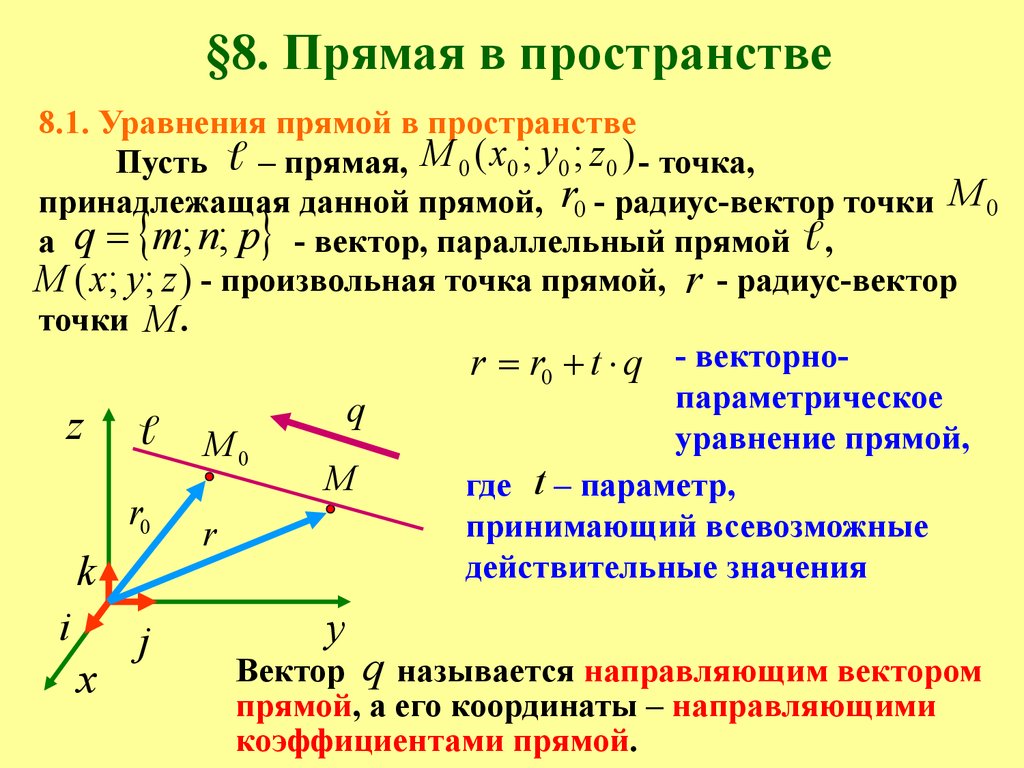
8.1. Уравнения прямой в пространстве
Пусть – прямая, М 0 ( x0 ; y0 ; z0 ) - точка,
принадлежащая
данной прямой, r0 - радиус-вектор точки М 0
,
а q m; n; p - вектор, параллельный прямой
М ( x; y; z ) - произвольная точка прямой, r - радиус-вектор
точки М .
- векторноr r0 t q
параметрическое
q
z М
уравнение прямой,
0
М
где t – параметр,
r0
принимающий всевозможные
r
действительные значения
k
i
j
x
y
Вектор q называется направляющим вектором
прямой, а его координаты – направляющими
коэффициентами прямой.

37.

x x0 t m
где
y y0 t n
z z0 t p
М 0 ( x0 ; y0 ; z0 ) q m; n; p
x x0 y y0 z z0
m
n
p
x x1
y y1
z z1
x2 x1 y2 y1 z 2 z1
параметрические
уравнения
прямой,
-
канонические уравнения
прямой
-
уравнения прямой,
проходящей через две точки
М 1 ( x1 ; y1 ; z1 ) и М 2 ( x2 ; y2 ; z2 )
-
Если прямую в пространстве рассматривать как
линию пересечения двух плоскостей, то ее можно задать
системой линейных уравнений двух плоскостей:
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
- общие уравнения прямой

38.

8.2. Направляющие косинусы прямой
Определение Направляющие косинусы вектора q m; n; p
называются направляющими косинусами прямой.
cos
m
m2 n2 p 2
cos
cos
p
m2 n2 p2
n
m2 n2 p 2

39.

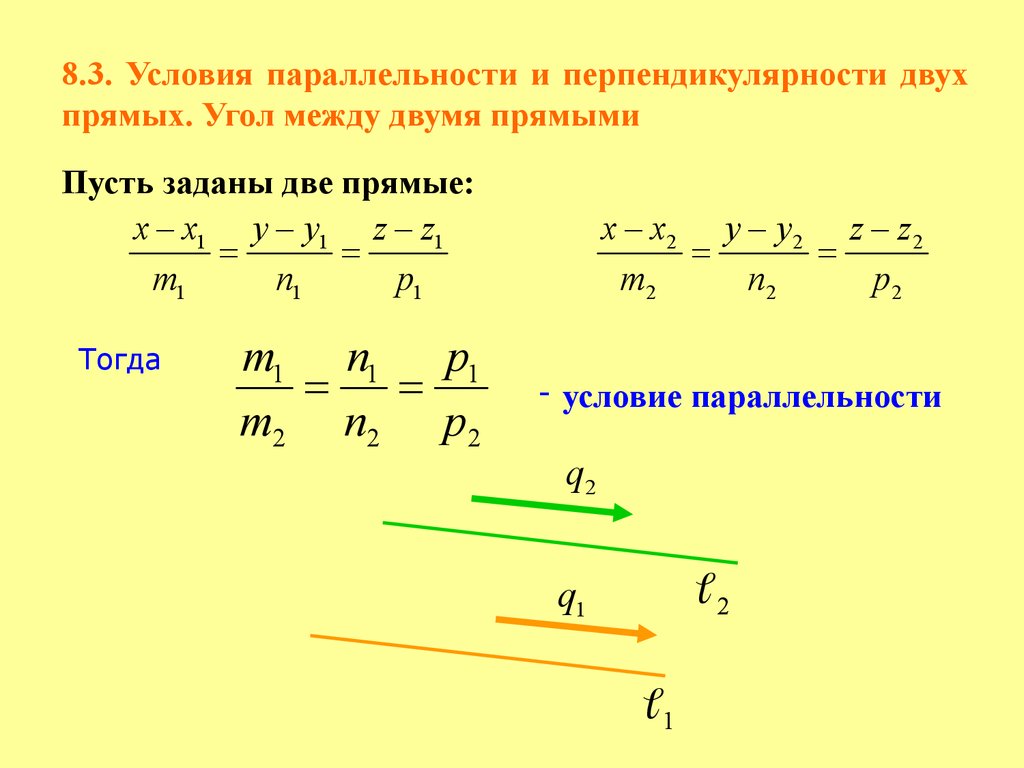
8.3. Условия параллельности и перпендикулярности двух
прямых. Угол между двумя прямыми
Пусть заданы две прямые:
x x1 y y1 z z1
m1
n1
p1
Тогда
m1 n1 p1
m2 n2 p2
x x2 y y 2 z z 2
m2
n2
p2
- условие параллельности
q2
q1
2
1

40.

m1 m2 n1 n2 p1 p2 0
q1
q2
- условие
перпендикулярности
1
1
q1
q2
2
cos
2
m1 m2 n1 n2 p1 p2
2
2
2
2
2
m1 n1 p1 m2 n2 p2
2
- угол между
прямыми

41.

§9. Плоскость и прямая
x x1 y y1 z z1
Пусть уравнение прямой:
m
n
p
а уравнение плоскости:
,
Ax By Cz D 0
Тогда
sin
A m B n C p
A B C m n p
2
2
2
2
2
q
n
Р
2
- угол между
прямой и
плоскость
ю

42.

A m B n C p 0
m n p
А В С
- условие перпендикулярности
n
q
n
Р
q
- условие параллельности
Р