Похожие презентации:
Середньоквадратичні зміщення
1. Середньоквадратичні зміщення
N1
r 2 (t ) [ ri (t ) ri (t 0)]2
N i 1
r 2 (t )
D lim
t
6t
Зв’язок середньоквадратичних
зміщень з коефіцієнтом самодифузії
Зв’язок середньоквадратичних
зміщень з автокореляційною
функцією швидкостей
t
6kBT
r (t )
( )(t )d
m 0
2
Чисельна перевірка:
2
r
(t ) (t )
2
t
Різницева схема:
f n 1 2 f n f n 1
2 f
|
2 t tn
t
t 2
2
2. Розрахунки в’язкості рідини
Компоненти тензора напруженьN
N 1
i 1
i 1 j i |1
N
(t ) m vi (t )vi (t ) rij (t )Fij (t )
Автокореляційною
функцією напружень
1
(t )
3Vk BT
Зсувна в’язкість
s (t )dt
0
(t ) (0)
3. Динамічний структурний фактор та спектральні функції потоків
Динамічні структурні факториS nn (k , ) Fnn (k , t )e dt
i t
0
Спектральні функції потоків
Cab (k , ) FJ a Jb (k , t )e dt
0
i t
4. Motivation
Визначення властивостейMotivation поширення
звука
в
середовищі
Numerical results for spectra of collective excitations in binary liquids
max Sii (k , ) i (k )
Bosse et al (1986) “Швидкий
звук” у дво-компонентній
рідкій системі Li4Pb (R~30)
max Cii (k , ) i (k )
Дисперсійні криві в
рідкому KrAr (R=2.09), з
Cii(k,ω)
5. Л.11. (NVT) та (NPT) ансамблі в молекулярній динаміці
• Мікроканонічний ансамбль (NVE): для досягнення робочоїтемператури необхідно перескальовувати швидкості частинок
• Канонічний ансамбль (NVT): температура встановлюється
взаємодією з термостатом, який змушує частинки мати середню
кінетичну енергію таку, що відповідає бажаній температурі
Термостати: Андерсена (1980) та Нозе (1984)
Термостат Андерсена: вважається, що кожна частинка з певною
ймовірністю взаємодіє з середовищем (термостатом) внаслідок
чого швидкість частинки може помінятись на таку, що
підкоряється розподілу Максвела-Больцмана при заданій
температурі.
6. (NVT) ансамбль з термостатом Андерсена
Ймовірність, що частинка буде мати стохастичне зіткнення зтермостатом у часовому кроці Δt є νΔt, де ν є випадковим числом.
Якщо частинка була вибрана для зіткнення, то її швидкість
вибирається випадковим чином з розподілу Максвела-Больцмана
при заданій температурі.
Алгоритм:
1. Знаходяться значення нових координат та швидкостей для всіх
частинок
2. В циклі по частинках генератор випадкових чисел з
ймовірністю ν вибирає певні частинки – всього N*
3. Для цих N* частинок визначаються нові швидкості
випадковим чином з розподілу Максвела-Больцмана
7. (NVT) ансамбль з термостатом Андерсена
Алгоритм:TEMP=0.0
DO I=1,N
X(I)=…
стандартний алгоритм
VX(I)=…
TEMP=TEMP+VX(I)**2
ENDDO
TEMP=TEMP/(S*N)
SIG=SQRT(TEMP)
DO I=1,N
IF(RANF().LT.NU*DT) THEN
VX(I)=GAUSS(SIG)
ENDIF
ENDDO
8. (NVT) ансамбль у формулюванні Нозе
Недолік термостату Андерсена – стохастичність швидкостей,втрата детерміністичності методу молекулярної динаміки.
Нозе запропонував розглядати традиційні рівняння руху N
частинок, додавши до системи ще одне рівняння руху для
термостату. Термостат має свою ефективну координату та
швидкість.
Лагранжіан системи:
N
LNose
Рівняння руху:
LNose
pi
mi s 2 v
vi
mi 2 2
Q 2
s vi U (r ) s g ln s
2
i 1 2
LNose
ps
Qs
s
9. (NVT) ансамбль з термостатом Нозе-Гувера
(NVT) ансамбль з термостатом НозеГувераГувер запропонува деяку модифікацію рівнянь руху:
U (r )
pi
pi
ri
.
pi2
( K (T )) / Q
i mi
.
.
m ri pi
.
s s
K(T) – кінетична енергія системи, що відповідає заданій
температурі
Алгоритм – стандартний Верле лише для N частинок + 1 термостат
10. Ланцюжок термостатів Нозе-Гувера
Термостат Нозе-Гувера не забезпечує канонічного розподілу уфазовому просторі 6N змінних. Для створення канонічного
розподілу у фазовому просторі було запропоновано
використовувати ланцюжок з M термостатів
U (r )
pi
1 pi
ri
.
pi2
1 ( K (T )) / Q1 1 2
i mi
.
.
j (Q j 1 2 j 1 K (T )) / Q j j j 1
.
M (QM 1 2 M 1 K (T )) / QM
.
m ri pi
.
s j s j j
11. (NPT) ансамбль з баростатом та термостатом
Паррінелло та Рахман запропонували зробити об’єм МД коміркизмінним для того, щоб у симуляціях підтримувати постійний тиск
системи.
Збільшення об’єму по осі X
для зменшення миттєвого
значення компонент тензору
Алгоритм:
тиску Pxx
1. Знаходяться значення нових координат та швидкостей для всіх
частинок
2. Озраховується миттєве значення всіх компонент тензору тиску
– в залежності від різниці з заданим тиском об’єм або
збільшується або зменшується
3. Для всіх N частинок перенормовуються компоненти
координат у відповідних пропорціях Lnew/Lold
12.
Використання (NPT) ансамблю длягенерування границі розділу
p0
p0
p0
crystal
liquid
•(NVT) ensemble
•(NPT) ensemble
p0
crystal
potential problem Vsol/Vliq ?
potential problem <Pn>=<Pt>
13.
Ансамбль (NPnTA) для дослідженняграниць розділу
Lennard-Jones two-phase
coexistence at 83K and
zero pressure
Ice/water interface at 230K and
1 bar pressure
Флуктуації Lz сторони МД комірки у (NPnTA) симуляціях
об’ємів твердих тіл та границь розділу рідина-кристал
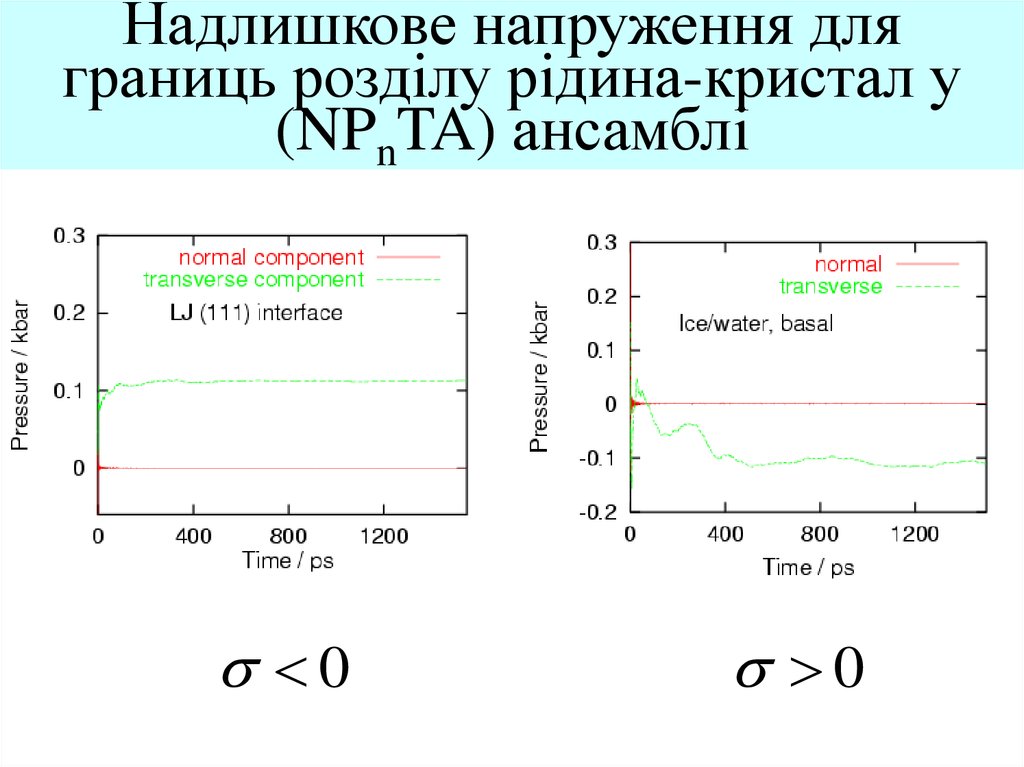
14. Надлишкове напруження для границь розділу рідина-кристал у (NPnTA) ансамблі
00













 Информатика
Информатика








