Похожие презентации:
Розрахунок часових кореляційних функцій
1. Л.9. Розрахунок часових кореляційних функцій
Часові кореляційні функціїFAB (k , t ) A(k , t ) B* (k , t 0)
Властивості часових кореляційних функцій
B(k , t ) A* (k , t 0) A(k , t ) B* (k , t 0)
*
FAA (k , t ) |t 0 A(k , t ) |t 0 A (k , t 0) 0
t
t
*
FAB ( k , t ) A( k , t ) B ( k , t 0)
t
t
*
A( k , t ) B ( k , t ) |t 0
t
2. Короткочасові розклади часових кореляційних функцій
Часові автокореляційні функції4
1 2 FAA
1
FAA
2
4
FAA (k , t ) FAA (k , t 0)
|
t
|
t
...
t 0
t 0
2
4
2! t
4! t
1 2
1 4
2
4
FAA ( k , t 0)[1 t t ...]
2!
4!
2n
- частотні моменти
1
2
2n
FAA
2n
n
S AA (k , )d ( 1) t 2n |t 0
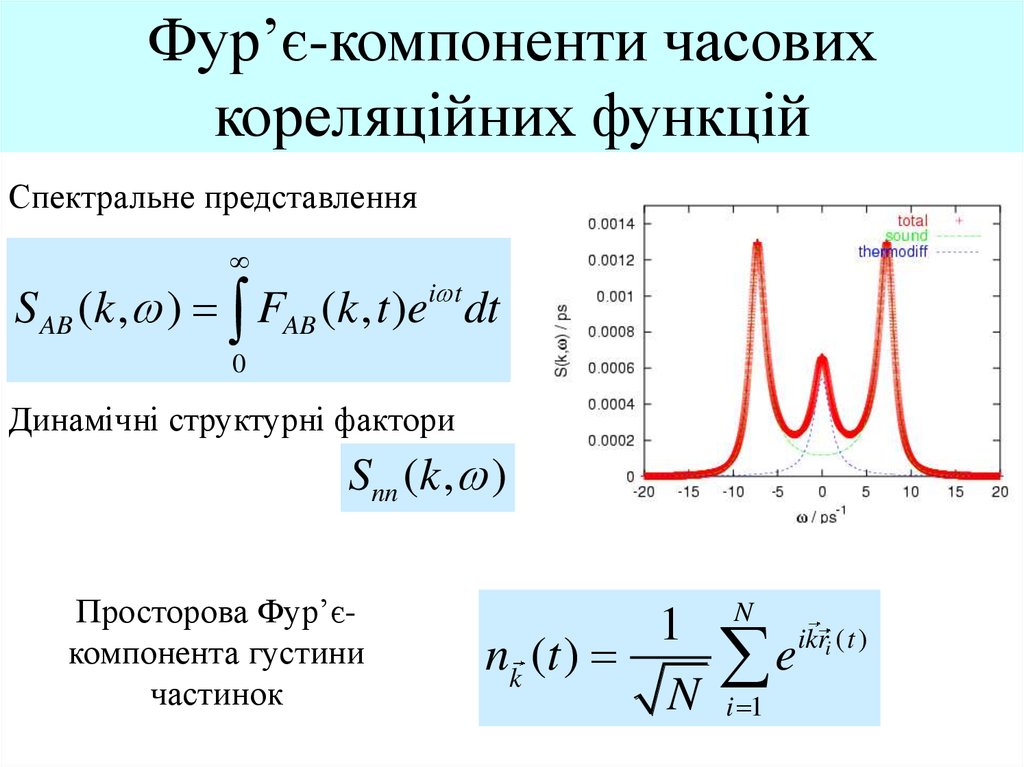
3. Фур’є-компоненти часових кореляційних функцій
Спектральне представленняS AB (k , ) FAB (k , t )ei t dt
0
Динамічні структурні фактори
Snn (k , )
Просторова Фур’єкомпонента густини
частинок
1
nk (t )
N
N
e
i 1
ikri ( t )
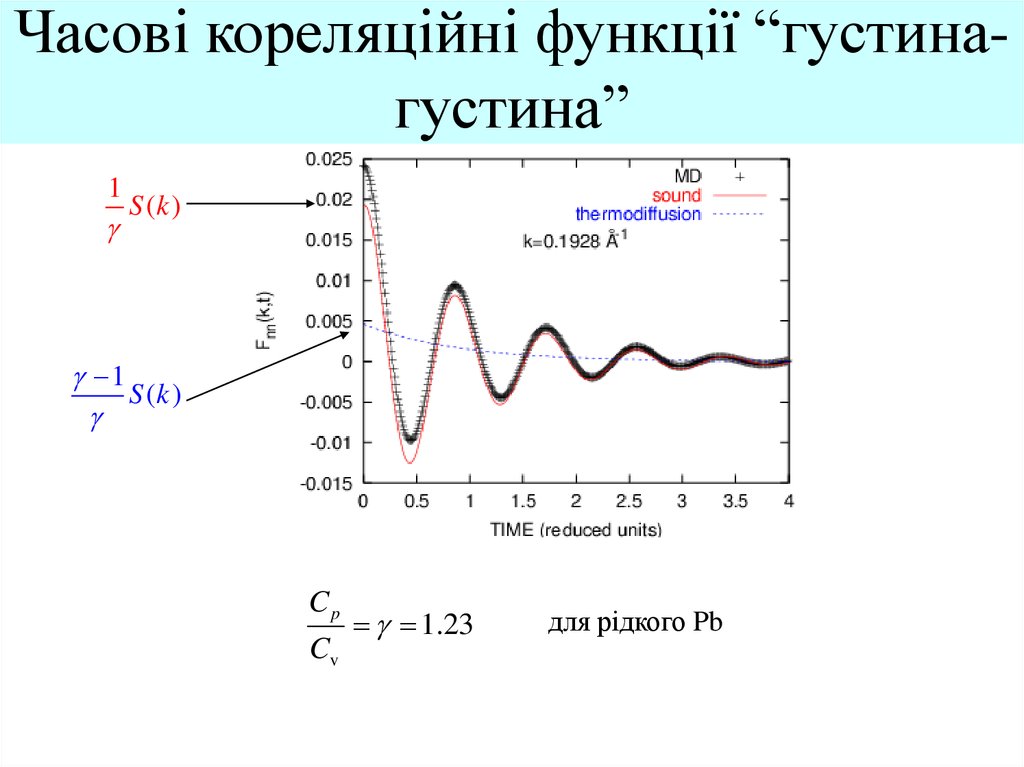
4. Часові кореляційні функції “густина-густина”
Часові кореляційні функції “густинагустина”1
S (k )
1
S (k )
Cp
Cv
1.23
для рідкого Pb
5. Повздовжний та поперечний потоки частинок
mJ k (t )
N
Просторова Фур’є-компонента
густини потоку частинок
v e
i 1
ikri ( t )
i
1
J k (kJ k )
k
Повздовжнякомпонента
густини потоку частинок
L
Поперечна компонента густини
потоку частинок
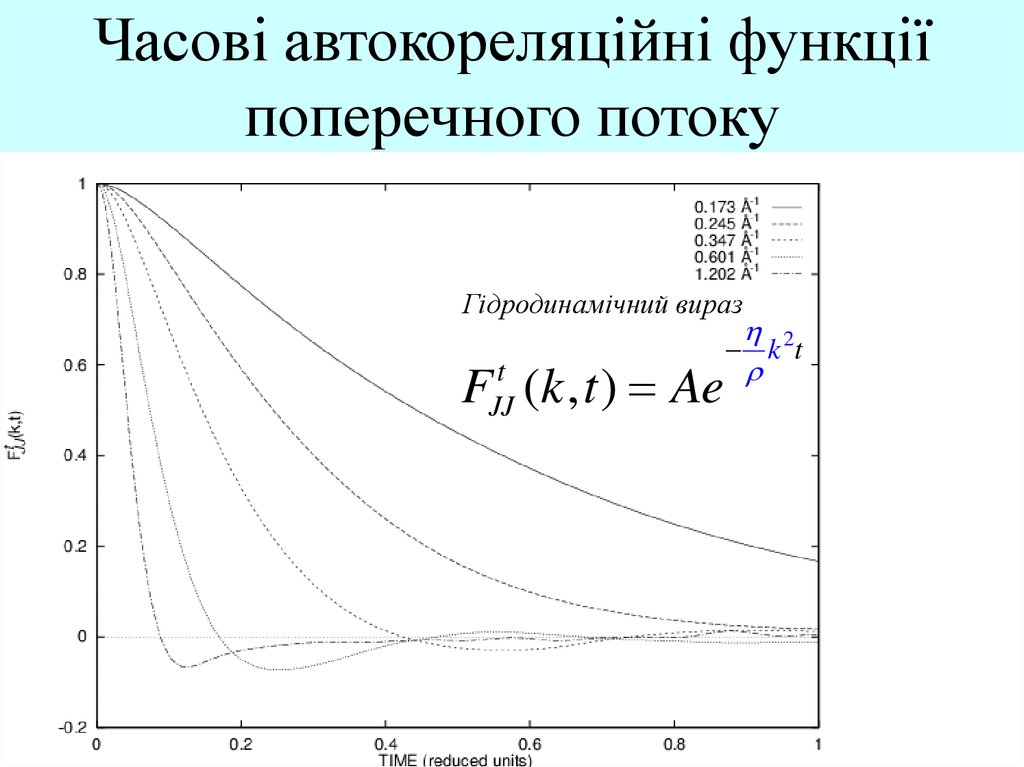
Автокореляційна функція
поперечного потоку
N
1
J k [k J k ]
k
T
F (k , t ) J k (t ) J k (t 0)
T
JJ
T
T*
6. LJ liquid mixture KrAr, 116 K
Часовіавтокореляційні
функції
LJ liquid
mixture KrAr,
116 K
MD-derived
transverse current-current
TCFs
поперечного
потоку
Гідродинамічний вираз
F (k , t ) Ae
t
JJ
2
k t
7. Рівняння неперервності
Просторова Фур’є-компонентагустини потоку частинок
nk (t )
t
m
J k (t )
N
N
v e
i 1
ikri ( t )
i
i
ik L
kJ k (t ) J k (t )
m
m
Співвідношення між
динамічним стректурним
фактором та спектральною
функцією потоку
m
S JJ (k , ) 2 Snn (k , )
k
2
2
8. Розрахунок часових кореляційних функцій за допомогою статистичних усереднень
Алгоритм розрахунку часових кореляційних функцій1. Задається довжина N часової кореляційної функції та відстань M
між початковими моментами (t=0)
N
M
2. Для кожного початкового моменту розраховується N добутків
(A(1)B(I)) та (B(1)A(I)) для I=1,N та їхнє середнє
[(A(1)B(I)) + (B(1)A(I))]/2 сумується.
3. Сума нормується на кількість усереднень (які можуть
відрізнятись для різних I !!!)
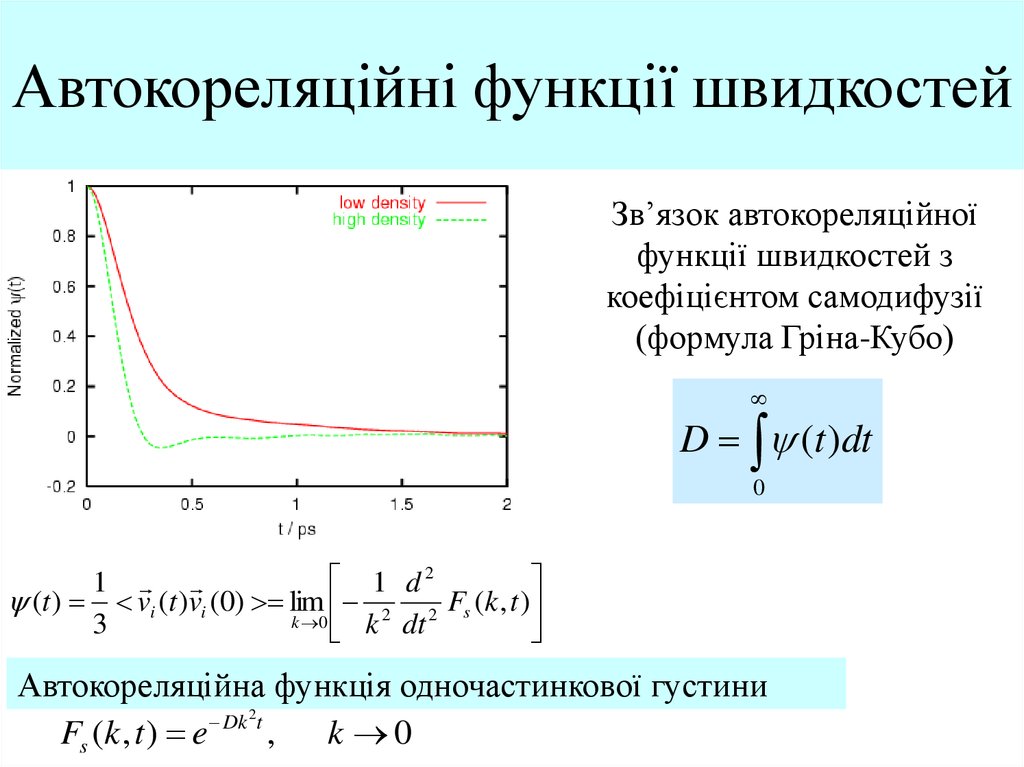
9. Автокореляційні функції швидкостей
Зв’язок автокореляційноїфункції швидкостей з
коефіцієнтом самодифузії
(формула Гріна-Кубо)
D (t )dt
0
1 d2
1
(t ) vi (t )vi (0) lim 2 2 Fs (k , t )
k 0
3
k dt
Автокореляційна функція одночастинкової густини
Dk 2t
Fs (k , t ) e
,
k 0
10. Середньоквадратичні зміщення
N1
r 2 (t ) [ ri (t ) ri (t 0)]2
N i 1
Зв’язок середньоквадратичних
зміщень з коефіцієнтом самодифузії
r 2 (t )
D lim
t
6t
Зв’язок середньоквадратичних зміщень з
автокореляційною функцією швидкостей
t
6kBT
r (t )
( )(t )d
m 0
2
11. Розрахунки в’язкості рідини
Компоненти тензора напруженьN
N 1
i 1
i 1 j i |1
N
(t ) m vi (t )vi (t ) rij (t )Fij (t )
Автокореляційною
функцією напружень
1
(t )
3Vk BT
Зсувна в’язкість
s (t )dt
0
(t ) (0)
12. Motivation
Визначення властивостейMotivation поширення
звука
в
середовищі
Numerical results for spectra of collective excitations in binary liquids
max Sii (k , ) i (k )
Bosse et al (1986) “Швидкий
звук” у дво-компонентній
рідкій системі Li4Pb (R~30)
max Cii (k , ) i (k )
Дисперсійні криві в
рідкому KrAr (R=2.09), з
Cii(k,ω)








 Информатика
Информатика








