Метод молекулярної динаміки для (NVE) ансамблю

1. Л.4 Метод молекулярної динаміки для (NVE) ансамблю

(NVE) ансамбль: постійні кількість частинок, об’єм, енергія
Початкова конфігурація – кристалічна гратка
Як отримати, наприклад, рідину при Tref ?
1. Необхідно розплавити початкову гратку при високій
температурі (Thigh ~Tref +500K)
2. Поволі опустити температуру системи з Thigh до Tref
3. Провести еквілібрацію при температурі Tref

2. Перенормування температури

mi vi2 (t )
T (t )
i 1 k B N deg. freedom
N
N deg. freedom 3N 3
-миттєва температура системи
-число ступенів вільності в
однокомпонентній однорідній системі
mi ( vi ) (t )
Tnew (t ) T (t )
i 1 k B N deg. freedom
N
2
-бажану температуру
можна отримати
перенормувавши
швидкості частинок
Кожних 20-30 кроків миттєву температуру треба перенормовувати
на бажаний рівень, аж поки система не прийде в рівновагу і буде
підтримувати задану температуру. При перенормуванні температури
енергія не зберігається – ми штучно або додаємо або забираємо
частину енергії.

3. Обчислення сил, що діють на частиннки

Fi (t ) E pot ( ri )
E pot ( ri ) U ( ri rj )
j i
- потенціальна енергія i-ї частинки
для випадку парних потенціалів
взаємодії
U ( xi x j )
Fx ,i (t ) (
)
rij
j i rij
- x-компонента сили,
що діє на частинку
rij ( xi x j )2 ( yi y j )2 ( zi z j )2
- відстань між
частинками

4. Обчислення сил, що діють на частиннки

U ( xi x j )
Fx ,i (t ) (
)
rij
j i rij
12 6
4
U LJ ( rij ) r12
r12
0
rcut
- в сумі по j-тих частинках
враховуються внески лише для
частинок в межах радіусу
взаємодії
rij rcut
rij rcut
2.5 - загальноприйнятий радіус обрізання
для LJ потенціалів
Що твориться з частинками на відстані
rij rcut ?

5. Чисельні алгоритми розв’язування рівнянь Ньютона

1. Алгоритм Верле
Розглянемо розклади у ряд Тейлора для координат
F (t ) 2
r (t t ) r (t ) v (t ) t
t O ( t 3 )
2m
F (t ) 2
r (t t ) r (t ) v (t ) t
t O ( t 3 )
2m
Їх сума:
F (t ) 2
r (t t ) r (t t ) 2r (t )
t O ( t 4 )
m

6. Алгоритм Верле

F (t ) 2
r (t t ) 2r (t ) r (t t )
t
m
t - часовий крок у МД
Різницева схема обчислення швидкості частинок, як
першої похідної по часу
r (t t ) r (t t )
v (t )
O ( t 2 )
2 t
Цей алгоритм дозволяє визначити швидкості лише коли нові
координати уже отримані, а тому він добре працює коли немає
потреби перенормовувати швидкості для контролю температури.

7. Розрахунок величин за допомогою функцій розподілу

4 N i
2
nij (r )
gij (r ')r ' dr '
V 0
r
Біжуче (залежне від відстані)
число сусідів i-го сорту
навколо частинок j-го сорту
4 N
sin(kr ) 2
S (k ) 1
( g ( r ) 1)
r dr
V 0
kr
Структурний
фактор

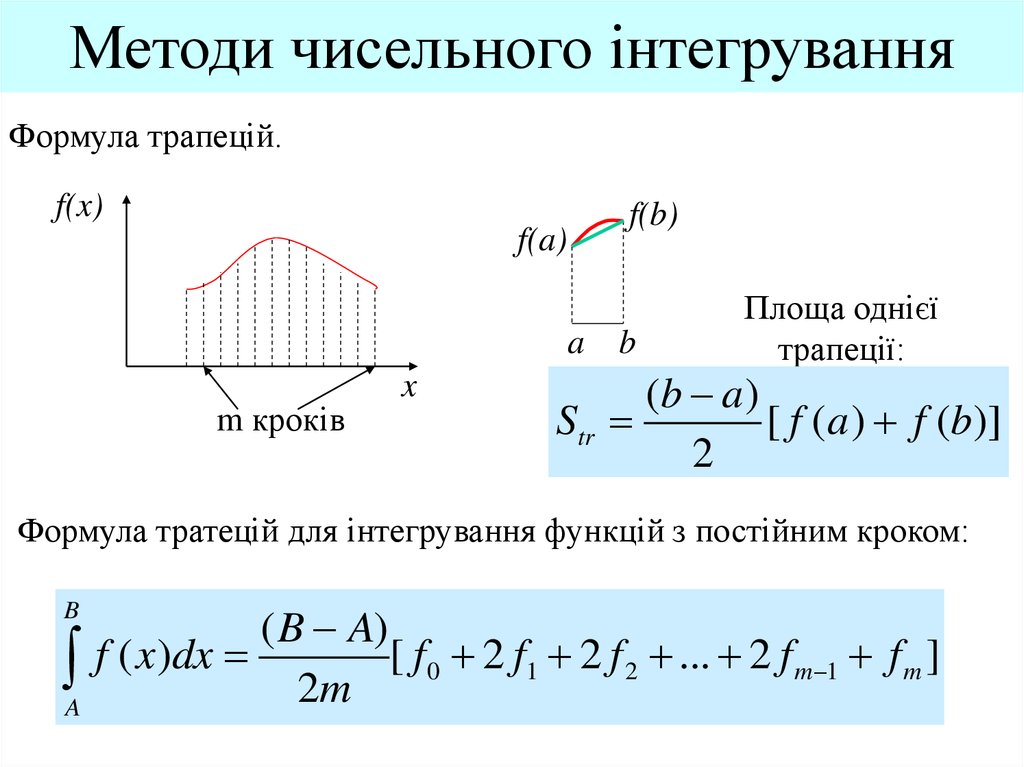
8. Методи чисельного інтегрування

Формула трапецій.
f(x)
f(a)
f(b)
a b
m кроків
x
Площа однієї
трапеції:
(b a )
Str
[ f (a ) f (b)]
2
Формула тратецій для інтегрування функцій з постійним кроком:
B
A
( B A)
f ( x )dx
[ f 0 2 f1 2 f 2 ... 2 f m 1 f m ]
2m

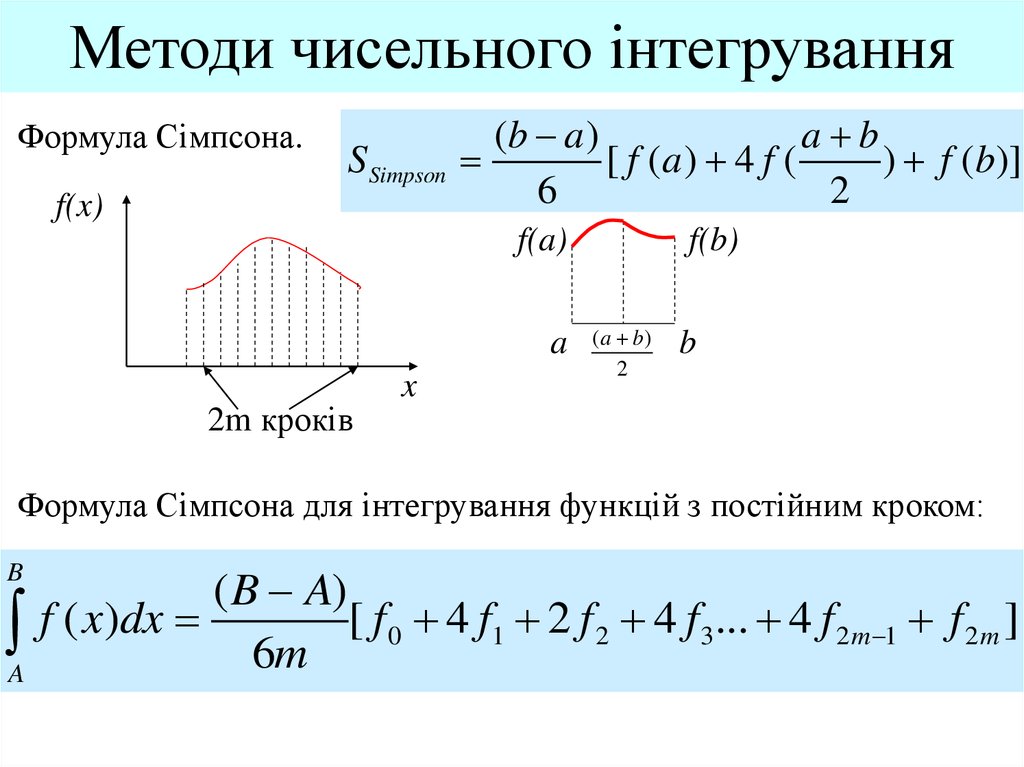
9. Методи чисельного інтегрування

Формула Сімпсона.
S Simpson
f(x)
(b a )
a b
[ f (a ) 4 f (
) f (b)]
6
2
f(a)
a
2m кроків
x
f(b)
( a b)
2
b
Формула Сімпсона для інтегрування функцій з постійним кроком:
B
A
( B A)
f ( x)dx
[ f 0 4 f1 2 f 2 4 f 3... 4 f 2 m 1 f 2 m ]
6m