Похожие презентации:
Розрахунок середньоквадратичних зміщень
1. Розрахунок середньоквадратичних зміщень
Алгоритм розрахунку часових кореляційних функцій1. Задається довжина N часової кореляційної функції та відстань M
між початковими моментами (t=0)
N
M
2. Для кожного початкового моменту розраховується 3N різниць
DX=X(I)-X(0), DY=Y(I)-Y(0), DZ=Z(I)-Z(0) для I=1,N і для
кожної перевіряються граничні умови.
3. Результат нормується на кількість усереднень (число частинок
сорту A,B та число різних функцій для кожного I)
r 2 (t ) | ri (t ) ri (0) |2
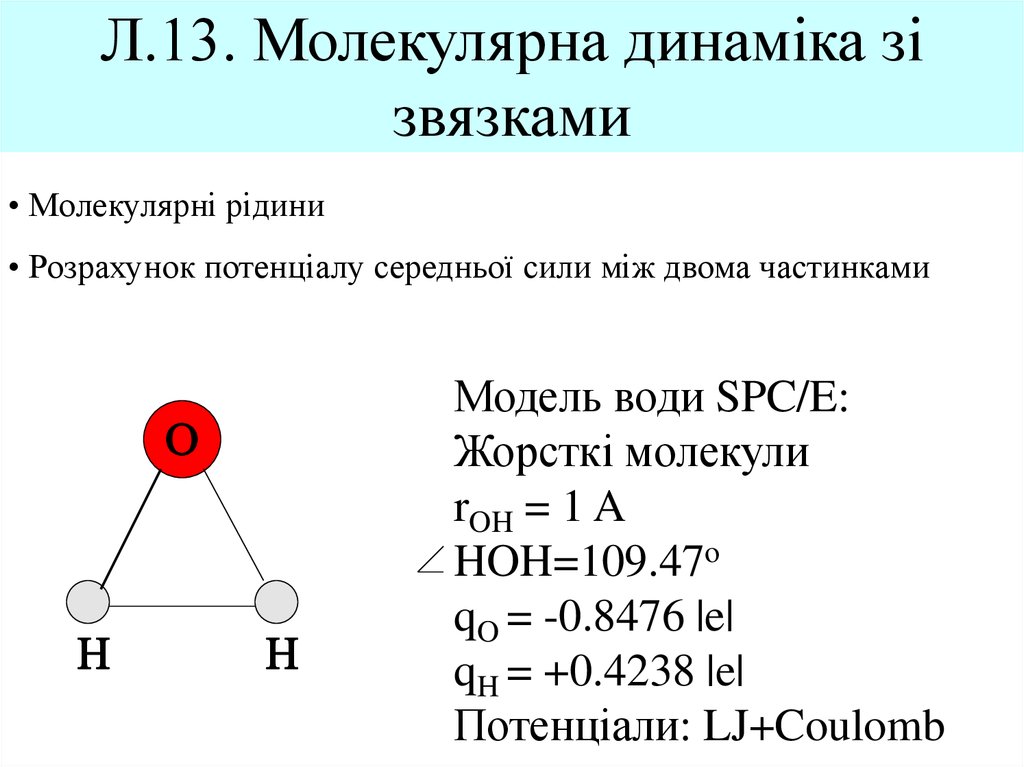
2. Л.13. Молекулярна динаміка зі звязками
• Молекулярні рідини• Розрахунок потенціалу середньої сили між двома частинками
O
H
H
Модель води SPC/E:
Жорсткі молекули
rOH = 1 A
HOH=109.47o
qO = -0.8476 |e|
qH = +0.4238 |e|
Потенціали: LJ+Coulomb
3. Рівняння руху динаміки зі звязками
Звязок накладений на відстань між атомами в молекулі(ri , rj ) rij2 dij2
Введемо Лагранжіан системи з α різними звязками
L K U (r N )
- невідомі множники Лагранжа
Рівняння руху:
d L L
dt q q
4. Рівняння руху динаміки зі звязками
Рівняння руху:U
mi qi
Fi Gi ( )
qi
qi
Щоб знайти невідомі множники Лагранжа будемо вимагати:
q
0
t
t
5. Рівняння руху динаміки зі звязками
Наприклад, частинка повинна рухатись по сфері радіусу d:1 2
(r d 2 )
2
Додаткова сила через наявність звязку:
G r
Для знаходження λ використовуємо
0 :
(rr ) r 2 0
Рівняння руху:
1
1
r ( F G) ( F r )
m
m
6. Рівняння руху динаміки зі звязками
Вважаючи, що зовнішня сила на частинку F=0, отримуємо:m
r2 r2 0
Множник Лагранжа:
mr 2
2
r
Тобто, додаткова сила що діє внаслідок накладеного звязку:
mr 2
G r 2 r m r
r
7. Алгоритм динаміки зі звязками
Різницева схема:r (t t ) 2r (t ) r (t t ) 2 t 2 r
Точність:
( t )
r (t t ) d [1
O( t 6 )]
6
4
2
2
Проблеми: похибка може акумулюватись
Для знаходження λ будемо використовувати умову точного
виконання звязку після кожного моменту часу :
r 2 (t ) d 2 0
r 2 (t t ) d 2 0
8. Алгоритм динаміки зі звязками
Різницева схема:r (t t ) 2r (t ) r (t t )
m
t r (t ) ru (t t )
2
m
t 2 r (t )
Звязок в момент t+Δt:
d [ru (t t )
2
m
t 2 r (t )]2
- квадратичне відносно λ рівняння, яке легко розв’язується
9. Алгоритм динаміки з багатьма звязками
Різницева схема:t
constrained
unconstrained
ri
(t t ) ri
(t t )
mi
2
l
k 1
k
i
Звязок в момент t+Δt через розклад у ряд Тейлора:
kc (t t ) ku (t t )
k
c
u
4
(
)
[
r
(
t
t
)
r
(
t
t
)]
O
(
t
)
i
riunc ( t t ) i
ri
i 1
N
k
(t )
10. Алгоритм динаміки з багатьма звязками
(t t ) 0c
k
Тому:
t
u
k (t t )
i 1 mi
N
2
k
k '
(
) r unc (t t ) (
) r unc (t ) k '
i
ri i
k ' 1 ri
l
Яке є матричним рівнянням:
ku (t t ) t 2 M
11. Алгоритм динаміки з багатьма звязками SHAKE
Ітеративна схема, щоб позбутись обертання великих матриць(t t ) 0
c
k
Застосовується не одночасно до
всіх звязків, а послідовно – звязок за звязком
2
t
constrained
unconstrained
ri
(t t ) ri
(t t )
i k (t )
mi
Тому:
k
1 k
(t t ) t k (
)runc (t t ) (
)r unc (t )
ri i
ri i
i 1 mi
N
u
k
2
12. Алгоритм динаміки з багатьма звязками SHAKE
Множники Лагранжа знаходяться просто для кожного k:k t
2
N
ku (t t )
k
1 k
m ( r
i 1
i
i
) r unc (t t ) (
i
ri
) r unc (t )
i











 Информатика
Информатика








