Похожие презентации:
Застосування квадратного тричлена при розв'язуванні задач з параметром
1. Застосування квадратного тричлена при розв'язуванні задач з параметром
КІРОВОГРАДСЬКЕ ТЕРИТОРІАЛЬНЕ ВІДДІЛЕННЯМАЛОЇ АКАДЕМІЇ НАУК УЧНІВСЬКОЇ МОЛОДІ
НАУКОВЕ ТОВАРИСТВО УЧНІВ «УМКА»
Застосування
квадратного тричлена
при розв'язуванні задач з
параметром
2. Мета:
Дослідити основний принципрозв’язування задач з параметрами ;
Застосувати найпростіші властивості
квадратного тричлена до знаходження ідеї
розв’язування задач з параметрами.
3.
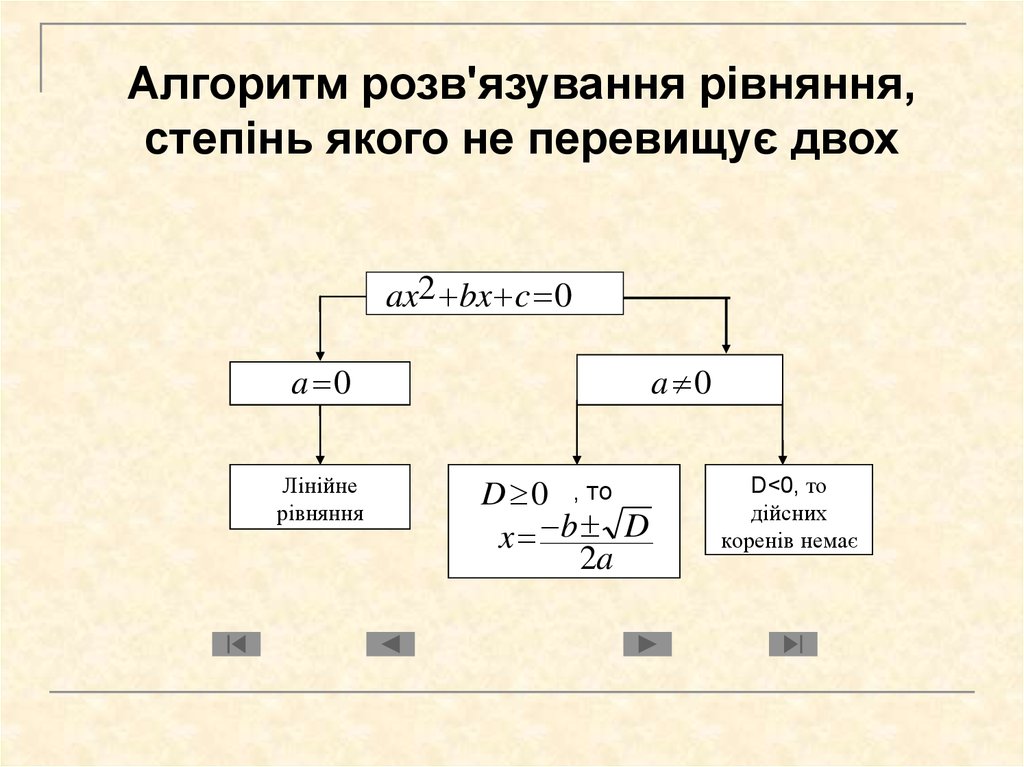
Алгоритм розв'язування рівняння,степінь якого не перевищує двох
ax2 bx c 0
a 0
Лінійне
рівняння
a 0
D 0 , то
x b D
2a
D<0, то
дійсних
коренів немає
4. «Каркас» квадратичної функції
D<0a>0
a<0
D=0
D>0
5.
Для кожного дійсного значення параметра арозв’язати рівняння:
x 2 6x 2 x a 1 a 7 0
. («КПІ»
2004 р.)
2
x
8 x 9 3a 0, a x 1,
2
x 6x 2 x a 1 a 7 0 2
x 4 x 5 a 0, a x 1.
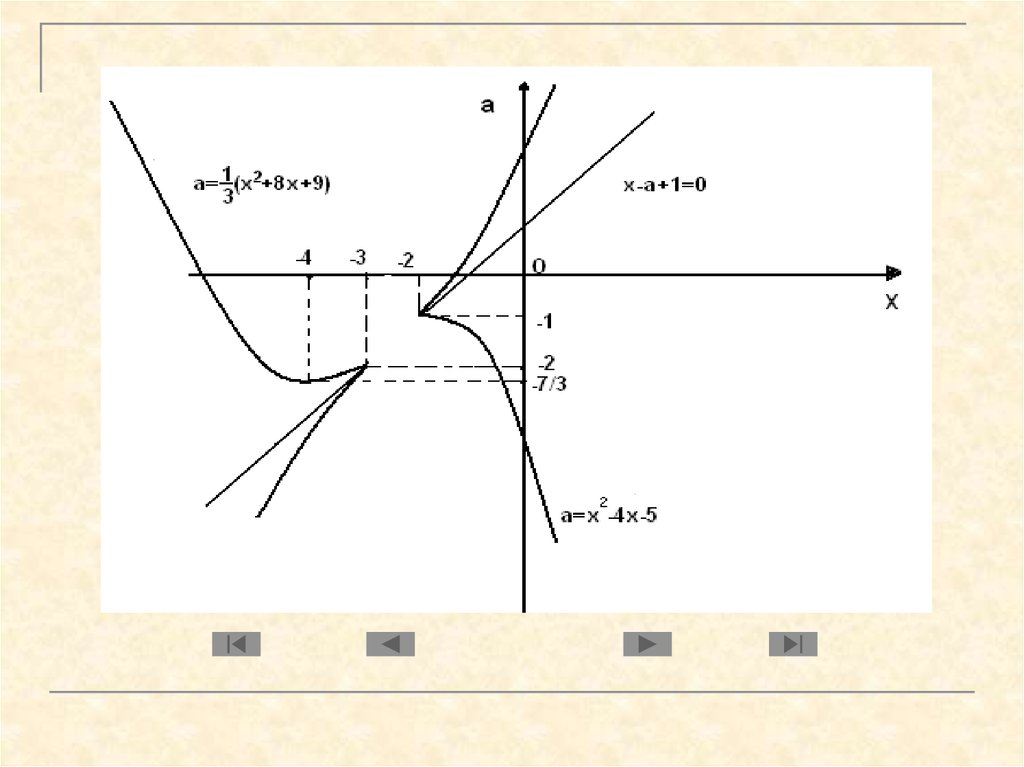
Скористаємось графіками залежностей a a(x)
1 2
a ( x) x 8 x 9
3
³
a( x) x 2 : 4 x 5.
6.
7.
7Відповідь: при a , x 2
3
1 a,
при
7
a ; 2 , x 2 1 a ; 4 7 3a ,
3
при
a 2; 1 , x 2 1 a ; 4 7 3a ,
при
a 1, x 4
7 3a .
.
8. Висновки:
Параметр, будучи фіксованим, але невідомимчислом, має подвійну природу.
Універсальних методів розв’язування задач з
параметрами не існує.
Задачі, пов’язані з розташуванням коренів
квадратичної функції, можна звести до
застосування теорем, які виведені з певних
властивостей квадратного тричлена.
Графічний метод має перевагу над
аналітичним у випадках, коли треба знайти
не самі розв’язки, а встановити їх кількість.






 Математика
Математика








