Похожие презентации:
Второй и третий признаки равенства треугольников. (7 класс)
1. Второй и третий признаки равенства треугольников.
7 класс.LOGO
5klass.net
2. План урока.
12
3
4
Проверка домашнего задания.
Математический диктант
Объяснение нового материала.
Решение задач.
3. Проверка домашнего задания.
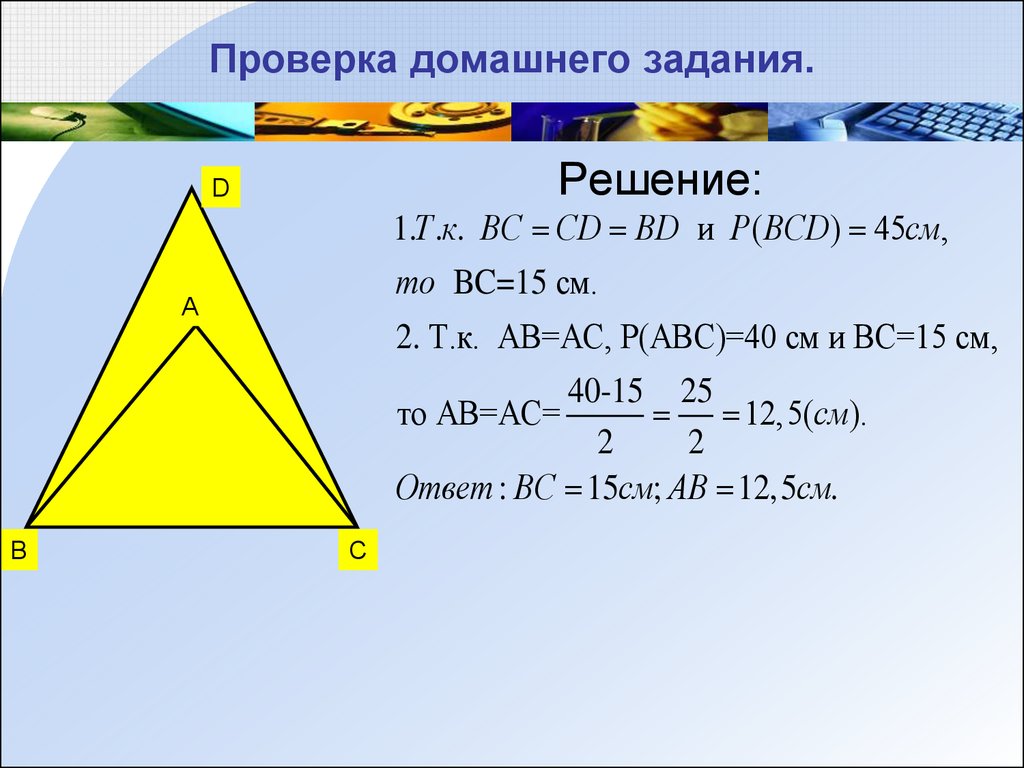
№ 108.Периметр равнобедренного треугольника
АВС с основанием ВС равен 40 см, а
периметр равностороннего треугольника
BCD равен 45 см.
Найдите стороны АВ и ВС.
Дано:
Найти:
ABC ;
AB AC ; P( ABC ) 40cм;
BCD; BC CD BD;
P( BCD) 45см.
АВ, ВС.
4. Проверка домашнего задания.
Решение:D
1.Т .к. BC CD BD и P( BCD) 45см,
то BC=15 см.
А
2. Т.к. АВ=АС, Р(АВС)=40 см и ВС=15 см,
40-15 25
то АВ=АС=
12,5(см).
2
2
Ответ : ВС 15см; АВ 12,5см.
В
С
5. Тест «Свойства равнобедренного треугольника»
1. Медиана в равнобедренномтреугольнике является его биссектрисой и
высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
2. Если треугольник равнобедренный, то
а) он равносторонний;
б) все углы равны;
в) два угла равны.
3. В каком треугольнике только одна его
высота делит треугольник на два равных
треугольника
а) в любом;
б) в равнобедренном;
в) в равностороннем.
4. Биссектриса в равностороннем
треугольнике является медианой и
высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
5. Если треугольник равнобедренный, то
а) он равносторонний;
б) любая его медиана является его
биссектрисой и высотой;
в) ответы а) и б) неверные.
6. В каком треугольнике любая его высота
делит треугольник на два равных
треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем
6. Тест «Свойства равнобедренного треугольника». Проверка.
1. Медиана в равнобедренномтреугольнике является его биссектрисой
и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
2. Если треугольник равнобедренный, то
а) он равносторонний;
б) все углы равны;
в) два угла равны.
3. В каком треугольнике только одна его
высота делит треугольник на два равных
треугольника
а) в любом;
б) в равнобедренном;
в) в равностороннем.
4. Биссектриса в равностороннем
треугольнике является медианой и
высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
5. Если треугольник равнобедренный, то
а) он равносторонний;
б) любая его медиана является его
биссектрисой и высотой;
в) ответы а) и б) неверные.
6. В каком треугольнике любая его
высота делит треугольник на два равных
треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем
7. Задача № 1.
Периметр равнобедренного треугольникаравен 70 см. Найдите стороны этого
треугольника, если его боковая сторона
относится к основанию как 5:4.
LOGO
8. Задача № 2.
Периметр равнобедренноготреугольника равен 48 см. Найдите
стороны этого треугольника, если его
основание составляет 0,4 боковой
стороны.
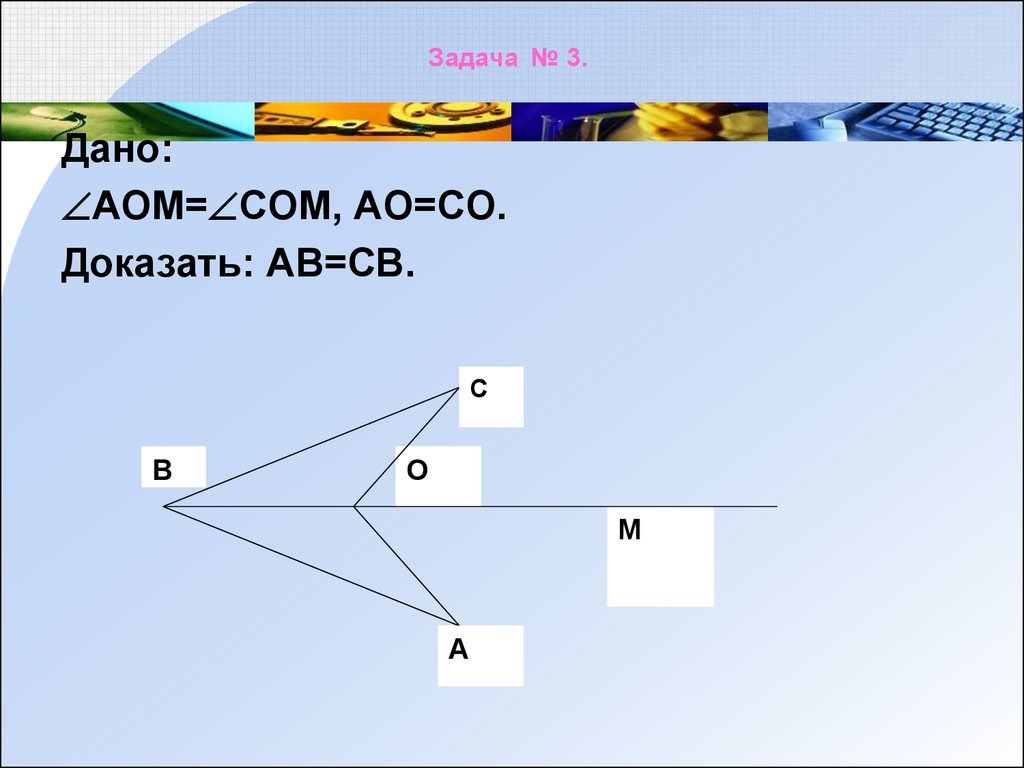
9. Задача № 3.
Дано:АОМ= СОМ, АО=СО.
Доказать: АВ=СВ.
С
В
О
М
А
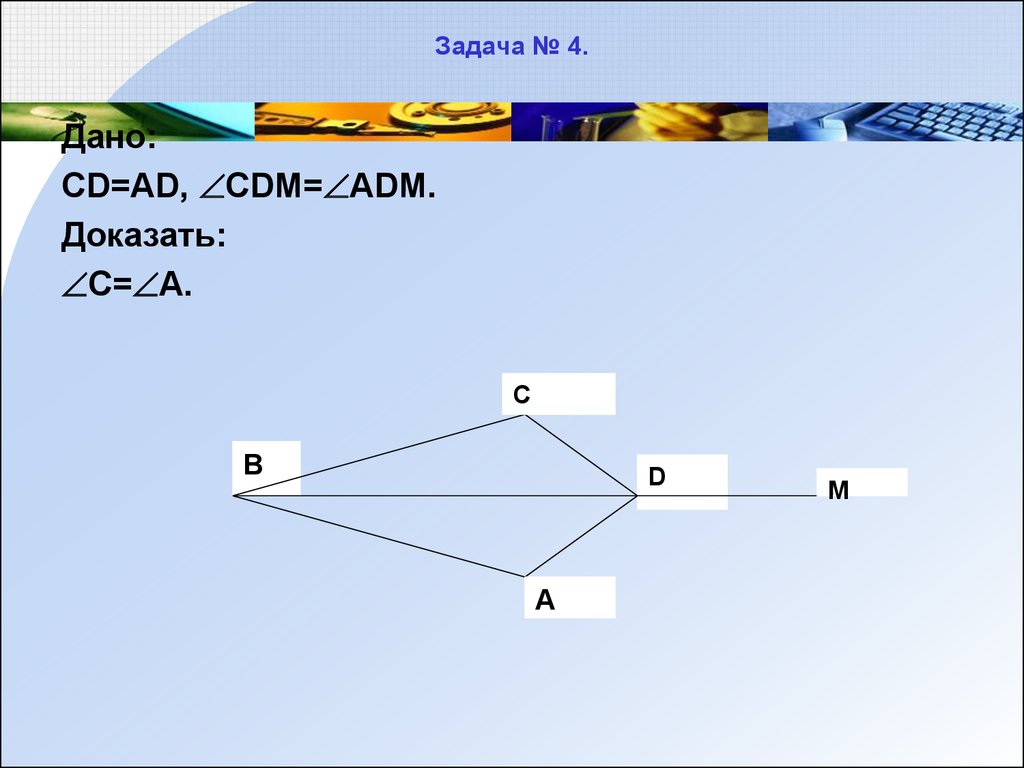
10. Задача № 4.
Дано:CD=AD, CDM= ADM.
Доказать:
C= A.
С
В
D
А
М
11. Задача № 5. В треугольнике АВС проведена медиана ВЕ. Найдите длину АЕ, если АВ=6 см, периметр треугольника АВС равен 18 см., а ВС на 2 см больше А
Решение задачЗадача № 5.
В треугольнике АВС проведена медиана ВЕ.
Найдите длину АЕ, если АВ=6 см, периметр
треугольника АВС равен 18 см., а ВС на 2 см
больше АВ.
Задача № 6.
Периметр треугольника равен 40 см.
Медиана делит данный треугольник на два
треугольника, периметры которых равны
28 см и 24 см. Найдите длину медианы.
12. Второй признак равенства треугольников
Если сторона и прилежащие к нейуглы одного треугольника
соответственно равны стороне и
прилежащим к ней углам другого
треугольника, то такие треугольники
равны.
Дано:
АВС; А1В1С1; АВ А1В1;
Доказать:
А А1 ; В В1.
АВС А1В1С1
13.
ВА
С
В1
А1
С1
14. Третий признак равенства треугольников
Если три стороны одного треугольникасоответственно равны трем
сторонам другого треугольника, то
такие треугольники равны.
Дано:
ΔАВС; ΔА1В1С1; АВ=А1В1; АС=А1С1;
ВС=В1С1.
Доказать: ΔАВС=ΔА1В1С1
15.
ВА
С
В1
А1
С1
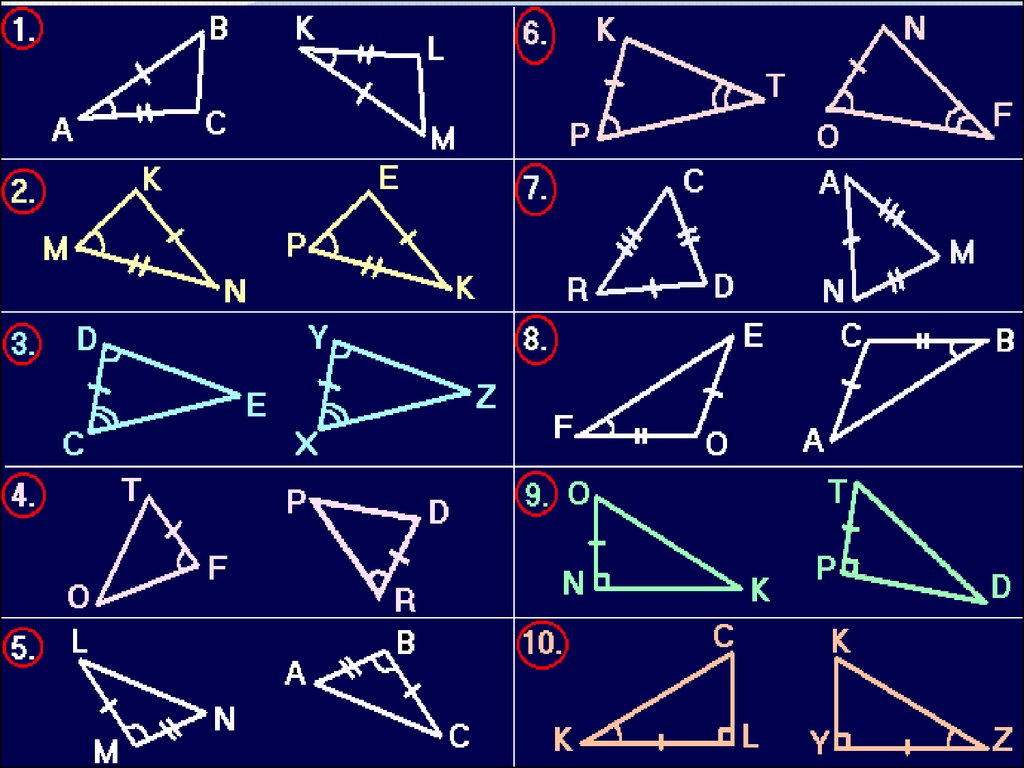
16. Признаки равенства треугольников
LOGO17.
18.
12
3
4
5
6
7
8
9
10
19.
12
3
4
5
6
7
8
9
10
I
II
I
III
II
20. Домашнее задание
12
3
№ 122.
Пункт 19.
Пункт 20.
4
№ 124.
21.
www.themegallery.comLOGO

















 Математика
Математика








