Скалярное произведение в координатах

1.

2.

B
C
6
3
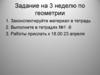
АВСD - прямоугольник
AD = 62 – 32 = 27 = 3 3
O
A
D
3 3
AВ АC =
AB
AО АD = AО
AD DC = 0
cos CAD
BAC =
AD
AB
AC
3
AC cos AB, AC = 3 6 6 = 9
AD cos AO, AD = 3 3 3
т.к. AD ^ DC
3 3 27
=
2
6

3.

Теорема
Скалярное произведение векторов
a {x1; y1}
выражается формулой
и
b {x2; y2}
a b = x1x2 + y1y2

4.

Следствие 1
Ненулевые векторы
a и b перпендикулярны тогда и
только тогда, когда
x1 x2 + y1 y2 = 0
a ^ b x 1 x 2 + y1 y 2 = 0
Пример
b {-2;
-2 11}
d { 2;
2 44}
+ =0
b ^d

5.

Следствие 2
Косинус угла между ненулевыми векторами
aи b
выражается формулой
cos a =
x 1 x 2 + y1 y 2
x12 + y12 x22 + y22

6.

Следствие 2
a b = x1x2 + y1y2
Доказательство:
2+ y 2
a
=
x
1
1
a b = a b cosa
cosa
=
a b
a b
=
2+ y 2
x
b
=
2
2

7.

Свойства скалярного произведения векторов
a b, c
Для любых векторов
,
справедливы равенства:
1
a 2 0
2
a b
3
(a + b) c
4
=
и любого числа
k
a 0
причем
a 2> 0
b a
Переместительный закон
=
при
a c + b c
Распределительный закон
(ka) b = k(a b)
Сочетательный закон

8.

a {3; -4}
b {-2; 1}
c {-2;-1,5}
Найдите
a b = 3 (-2) + (-4) 1 = - 10
тупой
b c = (-2) (-2) + 1 (- 1,5) = 2,5
острый
c a = 3 (-2) + (-4) (- 1,5) = 0
прямой
Перпендикулярны ли векторы
a и b, b и c, c и a
Каким (острым, тупым или прямым) является угол между
векторами
a и b, b и c, c и a

9.

a {4; -2}
i {1; 0}
c {-2;-1,5}
j {0; 1}
Найдите
a i
= 4 1 + (-2) 0 = 4
острый
c j
= (-2) 0 + (- 1,5) 1 = - 1,5
тупой
i j
= 1 0 + 0 1 = 0
Перпендикулярны ли векторы
прямой
a и i , c и j, i
и
j
Каким (острым, тупым или прямым) является угол между
векторами
a и i, c и j, i
и
j