Похожие презентации:
Линейное программирование
1.
1 блок – 25• Лекции – 5
• Практика – 5
• СР: Тест_1 – 5
• Текущий контроль – 10
2 блок – 35
• Лекции – 5
• Практика – 5
• СР – 13
• Индивидуальное кейсзадание (5)
• Тест_2 (5)
• Круглый стол,
конференции (3)
• Текущий контроль – 12
2. Лекция №1
Линейноепрограммирование
3.
Задача математического программирования:f ( x) max (min)
gi ( x) 0 , i 1, m1
gi ( x) 0 , i m1 1, m2
gi ( x) 0 , i m2 1, m
x j 0 , j 1, n1
x j любое , j n1 1, n ,
4.
f (x) (c, x) max (min)A m×n, (A i , x ) b i , i 1, m1
(A i , x ) bi , i m1 1, m 2
(A i , x ) bi , i m 2 1, m
x j 0 , j 1, n1
x j любое , j n1 1, n ,
(1)
5.
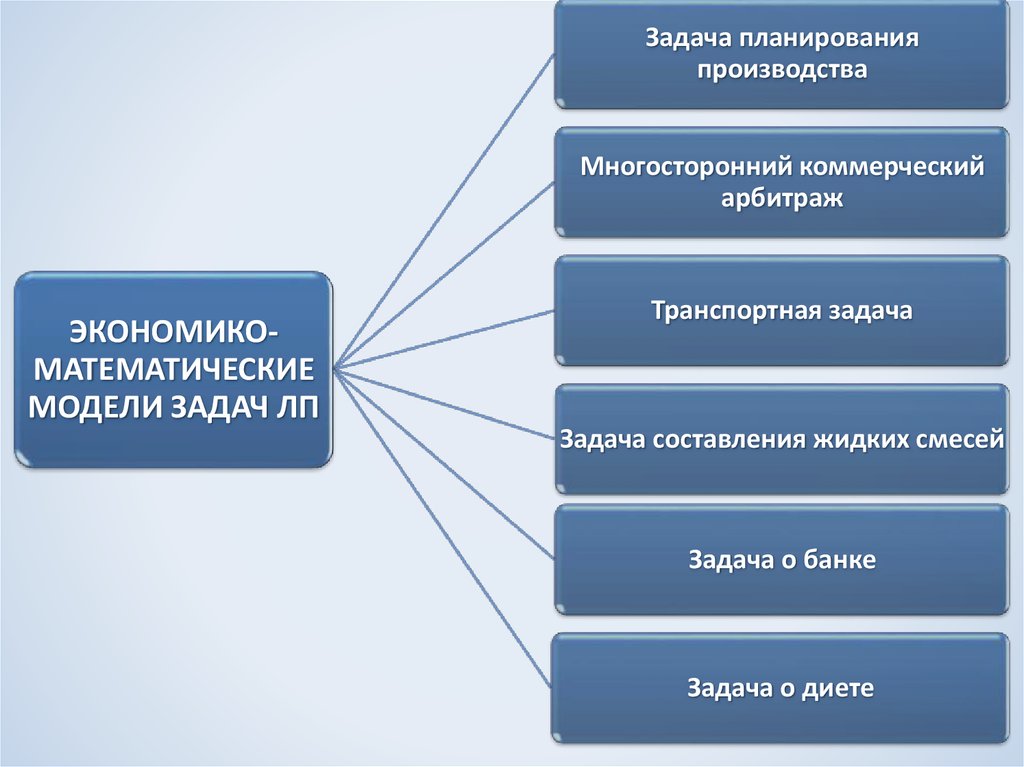
Задача планированияпроизводства
Многосторонний коммерческий
арбитраж
ЭКОНОМИКОМАТЕМАТИЧЕСКИЕ
МОДЕЛИ ЗАДАЧ ЛП
Транспортная задача
Задача составления жидких смесей
Задача о банке
Задача о диете
6.
Задача планирования производства.n – число типов товаров, m – число типов ресурсов.
aij 0, i 1,2,.., m, j 1,2,..., n, bi 0, c j 0
n
cjxj
max
n
bi , i 1,2,.., m
j 1
aij x j
j 1
x j 0, j 1,2,..., n
7.
Задача о диете.n – продуктов питания, m – число полезных веществ.
aij 0, i 1,2,.., m, j 1,2,..., n, bi 0, c j 0
n
cjxj
min
n
bi , i 1,2,.., m
j 1
aij x j
j 1
x j 0, j 1,2,..., n
8. Задача о банке
Собственные средства банка в сумме с депозитами составляют 100млн. $.
Не менее 35 млн. $ из этой суммы размещена в кредитах
Ликвидное ограничение: ценные бумаги должны составлять не
менее 30%, размещенных в кредитах и ликвидных активах.
Пусть х1 – средства (млн. $), размещенные в кредитах, х2 –
средства (млн. $), размещенные в ликвидных активах.
Балансовое ограничение:
х1+х2≤100
(*)
Кредитное ограничение:
х1≥35
(**)
Ликвидное ограничение:
х2≥0,3(х1+х2)
(***)
Условие неотрицательности:
х1≥0, х2≥0
(****)
с1-доходность кредитов, с2 –доходность ликвидных активов
f=c1x1+c2x2→max при условиях
(*)–(****)
9.
Стандартная форма задачи ЛП:n
f ( x) c j x j max
j 1
n
a x
j 1
ij
j
bi , i 1,2,..., m
x j 0, j 1,2,.., n
Каноническая форма задачи ЛП:
n
f ( x) c j x j max
j 1
n
a x
j 1
ij
j
bi , i 1,2,..., m
x j 0, j 1,2,.., n
10. Симплекс метод
f c, x maxСимплекс метод
Ax b, Am n (1)
x 0
1
2
m
Пусть A , A ,.., A - линейно независимые, то есть образуют базис.
B A1 , A2 ,.., Am , B 0
Таким образом, матрицу А можно записать A B
Систем у (1) перепишем в виде:
N .
Bx B Nx N b, x B x1 ,..., xm , x N xm 1 ,..., xn
x B B 1 Nx N B 1b, Z N B 1 N , Z 0 B 1b
~
x ~
x ,..., ~
x ,0,...,0
1
Z j B 1 A j
m
11. Начальная симплекс таблица
xx
B
f
C B , Z j C N
~
B
0
f C , Z
N
Z
Z
0
~
f
12. Начальная симплекс таблица. Возможные варианты. №1
f c , x maxAx b, b 0
x 0
Ax Ev b
x 0, v 0
~
~
Опорное решение: x 0, v b
~
v
f
x
A
b
-c
0
13. Начальная симплекс таблица. Возможные варианты. №2.
f c, x maxAx b, b 0
x 0
A E
~
A
Базисные переменные: x1 ,..., xm
Небазисные переменные: xm 1 ,..., xn
xN
x
B
f
~
A
b
~
f
14. Начальная симплекс таблица. Возможные варианты. №3
f c, x maxAx b, b 0
x 0
Вспомогательная задача:
F w1 w2 wm max
Ax w b, b 0
x 0, w 0
15.
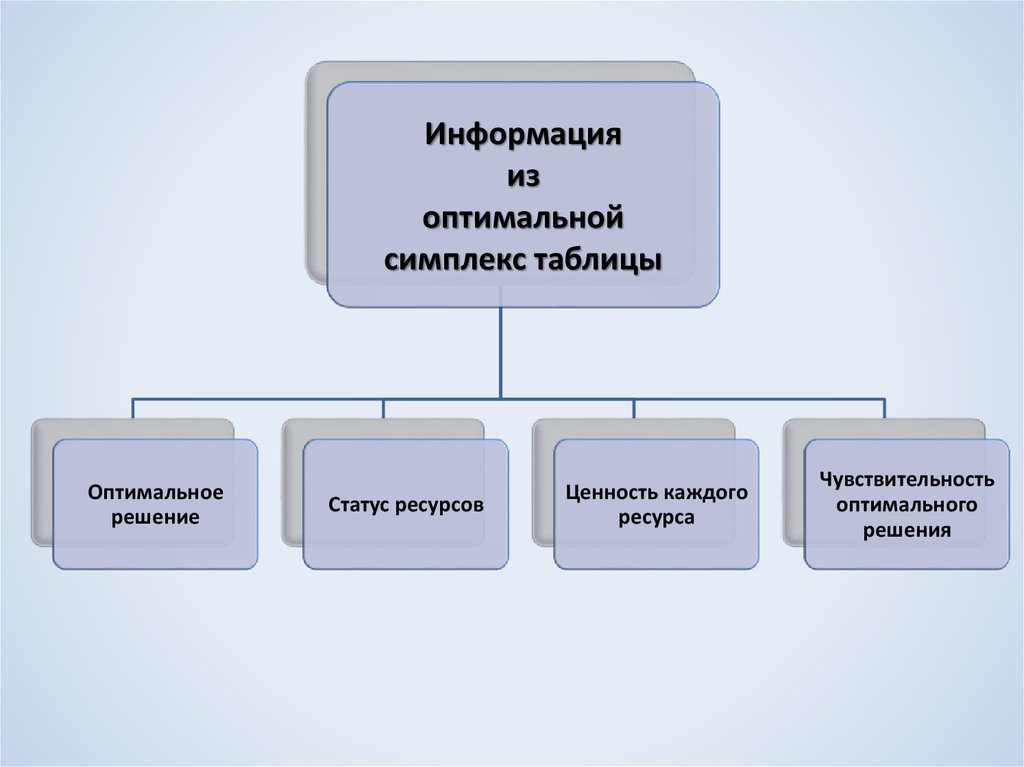
Информацияиз
оптимальной
симплекс таблицы
Оптимальное
решение
Статус ресурсов
Ценность каждого
ресурса
Чувствительность
оптимального
решения
16. Ценность ресурса
Ценность ресурса – характеризуется величиной улучшенияоптимального значения f , приходящегося на единицу прироста
данного ресурса
17.
Статус ресурсовДефицитный
Недефицитный


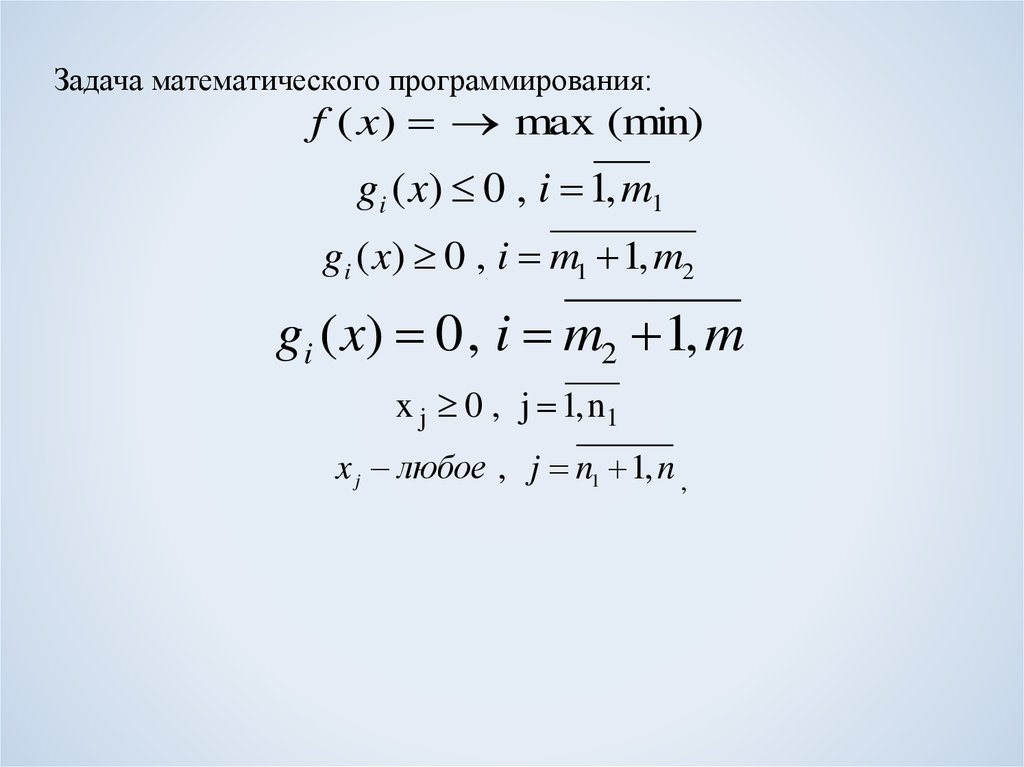
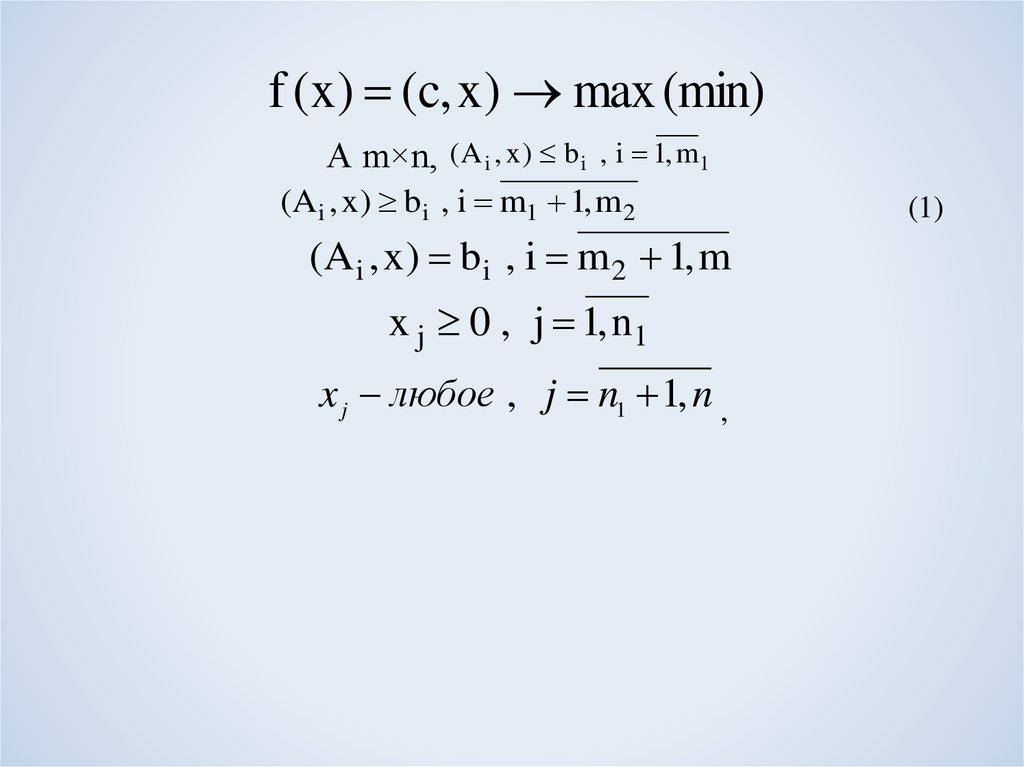











 Математика
Математика








