Приближение Фраунгофера в задачах дифракции

1. Физика колебаний и волн. Квантовая физика.

2. Лекция № 4

Приближение Фраунгофера в
задачах дифракции.
1. Условия приближения геометрической оптики, дифракции Френеля
и дифракции Фраунгофера.
2. Волновой параметр .
3. Дифракция плоской монохроматической волны на длинной прямой
щели .

3.

Йозеф ФРАУНГОФЕР
Joseph von Fraunhofer, 1787–1826
Немецкий физик и оптик, уроженец
Штраубинга (Straubing), сын
ремесленника-стеклодува. Рано
осиротев, пошел в подмастерья к
стекольщику. Явление дифракции
Фраунгофер исследовал с чисто
прикладной точки зрения: делом
своей жизни он считал изобретение
идеальных ахроматических линз,
которые не давали бы радужного
ореола вокруг изображения.

4.

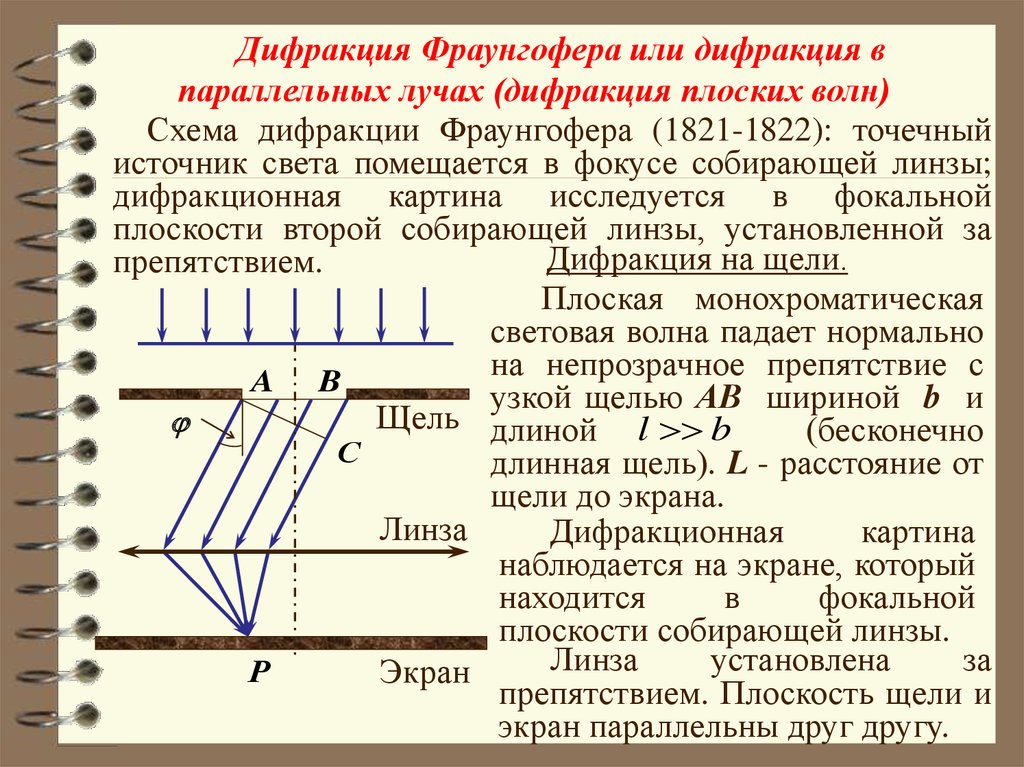
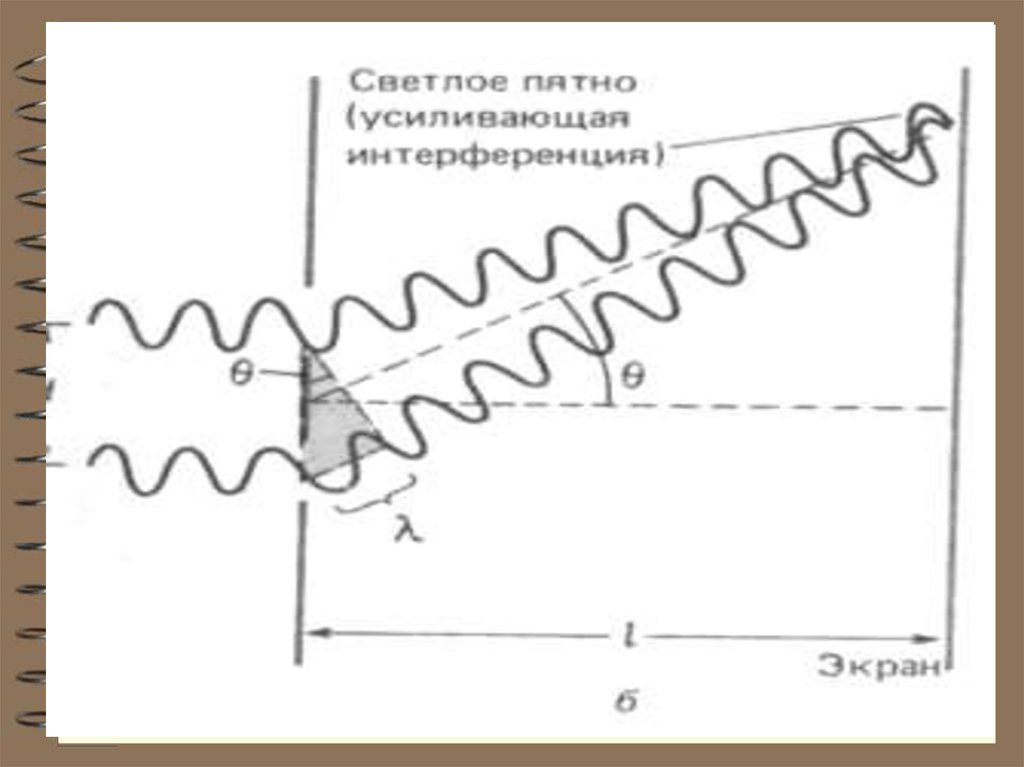
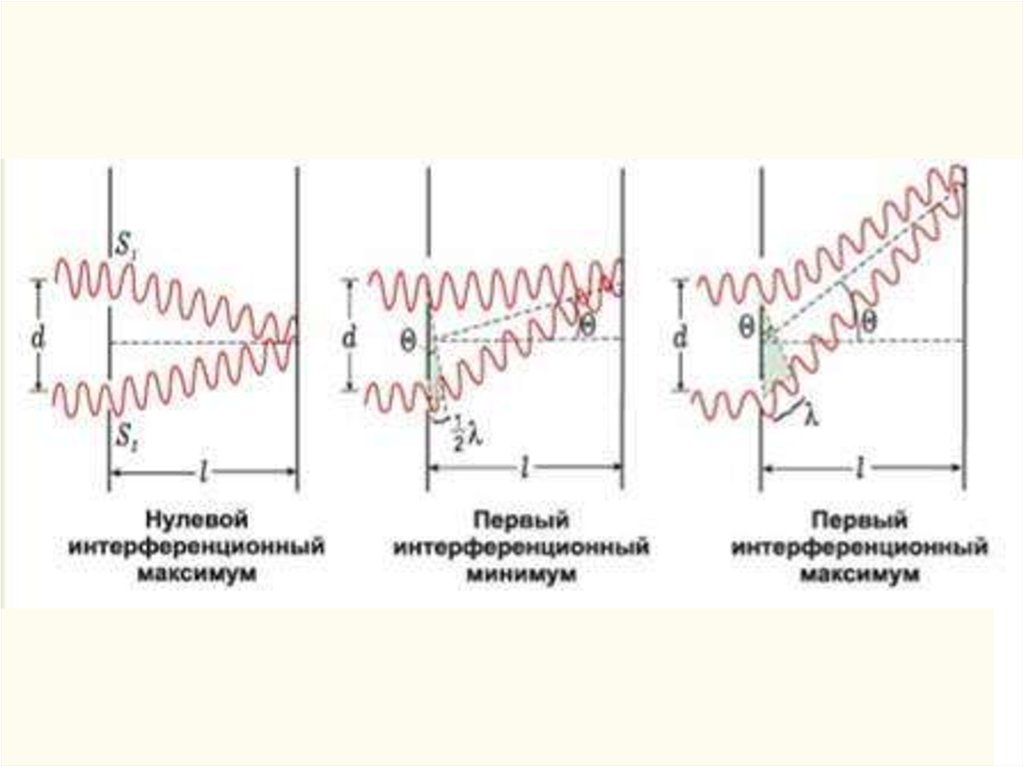
Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
Схема дифракции Фраунгофера (1821-1822): точечный
источник света помещается в фокусе собирающей линзы;
дифракционная картина исследуется в фокальной
плоскости второй собирающей линзы, установленной за
Дифракция на щели.
препятствием.
Плоская монохроматическая
световая волна падает нормально
на непрозрачное препятствие с
A B
узкой щелью АВ шириной b и
Щель длиной . l b
(бесконечно
С
длинная щель). L - расстояние от
щели до экрана.
Линза
Дифракционная
картина
наблюдается на экране, который
находится
в
фокальной
плоскости собирающей линзы.
Линза
установлена
за
P
Экран
препятствием. Плоскость щели и
экран параллельны друг другу.

5.

Условия приближения геометрической оптики,
дифракции Френеля и дифракции Фраунгофера.
Вид дифракционной картины на экране зависит
от величины волнового параметра
p
L
b
2
L
b
1) Если р<< 1 ( “широкая” щель)
L
<< 1 или b >> L - широкая щель
b
много больше размеров первой зоны Френеля и
распределение интенсивности света за щелью
можно получить с помощью обыкновенной
геометрической оптики.
2
b
Число Френеля Nф =
~ m ; Nф = р‾² ,
L
где m – число открытых зон Френеля. Nф >> 1.

6.

Условия приближения геометрической оптики,
дифракции Френеля и дифракции Фраунгофера.
Вид дифракционной картины на экране зависит
от величины волнового параметра
p
L
b
2
L
b
2) Если р ~ 1 - будет дифракция Френеля
L
L и распределение
~ 1 или b ~
b
интенсивности в плоскости наблюдения в
этом случае определяется числом зон Френеля,
укладывающихся на полуширине щели.
Число Френеля
b2
Nф =
L
~1 ;
Nф = р‾² ,

7.

Условия приближения геометрической оптики,
дифракции Френеля и дифракции Фраунгофера.
Вид дифракционной картины на экране зависит
от величины волнового параметра
p
L
b
2
L
b
3) Если р >> 1 - будет дифракция Фраунгофера
L
L - “узкая” щель.
>> 1 или b <<
b
b2
Число Френеля Nф =
<< 1 ; Nф = р‾² ,
L

8.

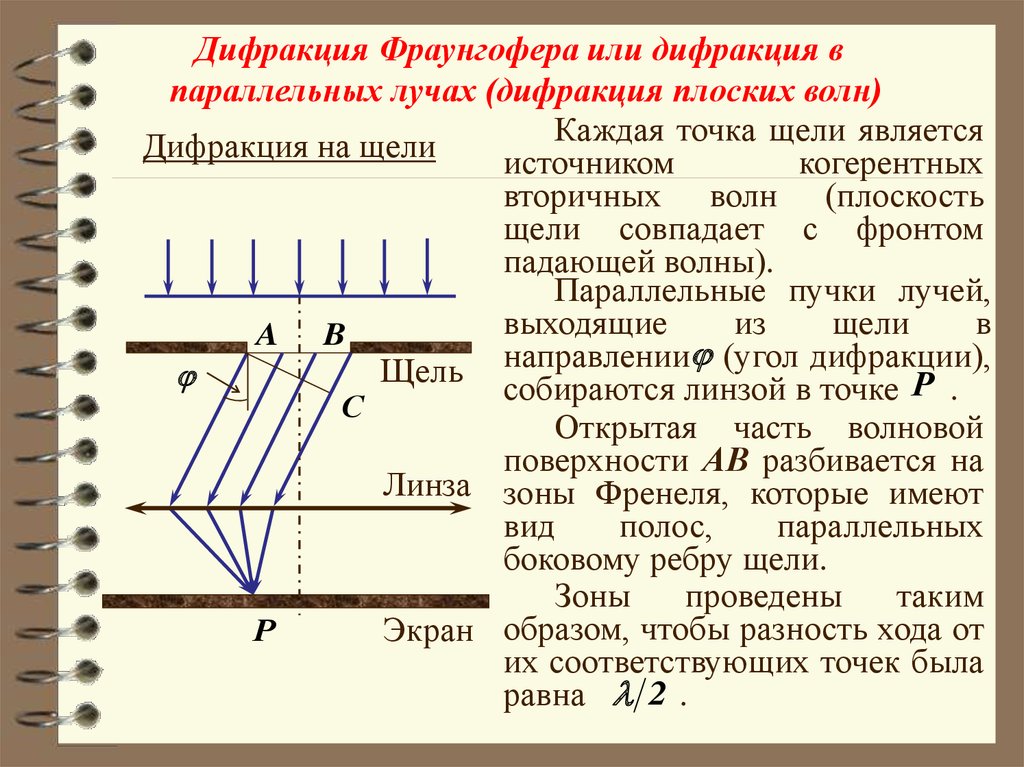
Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
Каждая точка щели является
Дифракция на щели
источником
когерентных
вторичных волн (плоскость
щели совпадает с фронтом
падающей волны).
Параллельные пучки лучей,
выходящие
из
щели
в
A B
Щель направлении (угол дифракции),
собираются линзой в точке P .
С
Открытая часть волновой
поверхности АВ разбивается на
Линза зоны Френеля, которые имеют
вид
полос,
параллельных
боковому ребру щели.
Зоны
проведены
таким
Экран образом, чтобы разность хода от
P
их соответствующих точек была
равна 2 .

9.

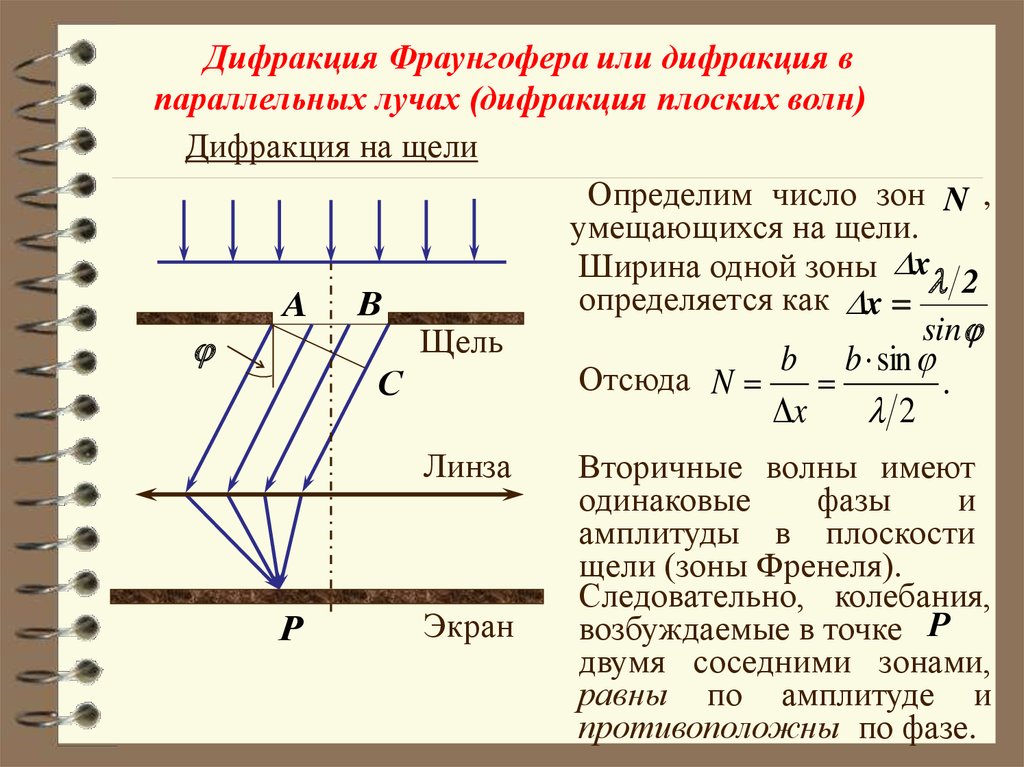
Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
Дифракция на щели
Определим число зон N ,
умещающихся на щели.
Ширина одной зоны x 2
определяется как x
A B
sin
Щель
b b sin
Отсюда
N
.
С
x
Линза
P
Экран
2
Вторичные волны имеют
одинаковые
фазы
и
амплитуды в плоскости
щели (зоны Френеля).
Следовательно, колебания,
возбуждаемые в точке P
двумя соседними зонами,
равны по амплитуде и
противоположны по фазе.

10.

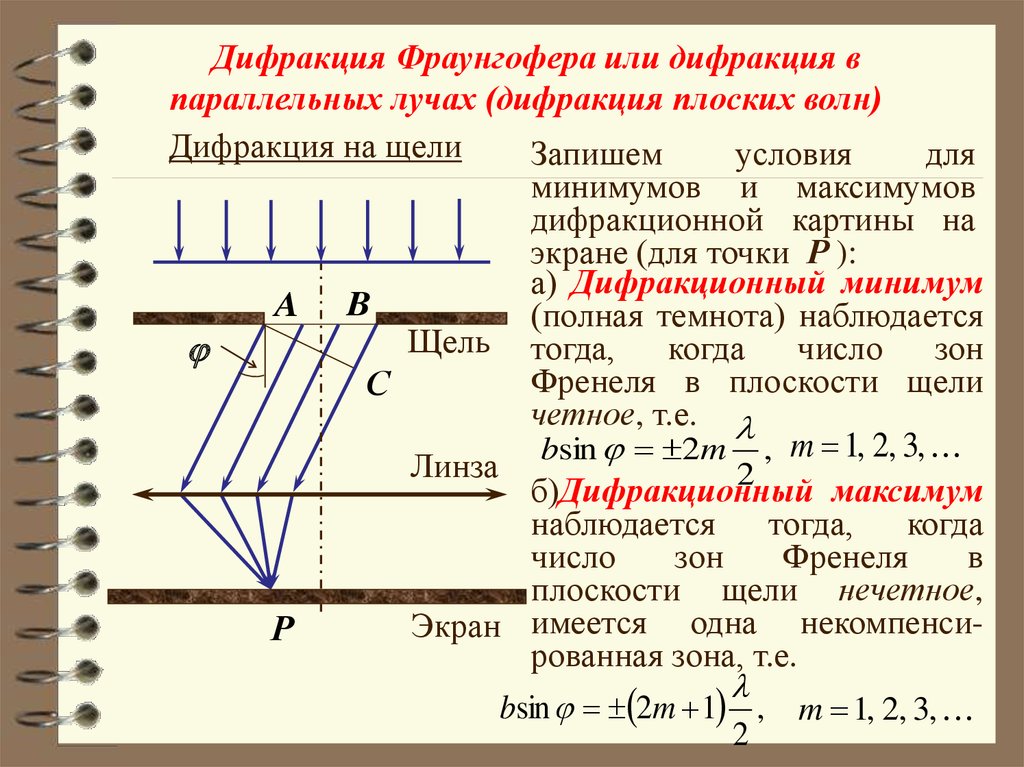
Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
Дифракция на щели
Запишем
условия
для
минимумов и максимумов
дифракционной картины на
экране (для точки Р ):
а) Дифракционный минимум
A B
(полная темнота) наблюдается
Щель тогда,
когда
число
зон
Френеля в плоскости щели
С
четное, т.е.
bsin 2m , m 1, 2, 3,
Линза
2
б)Дифракционный максимум
наблюдается
тогда,
когда
число
зон
Френеля
в
плоскости щели нечетное,
Экран имеется одна некомпенсиP
рованная зона, т.е.
bsin 2m 1 , m 1, 2, 3,
2

11.

Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
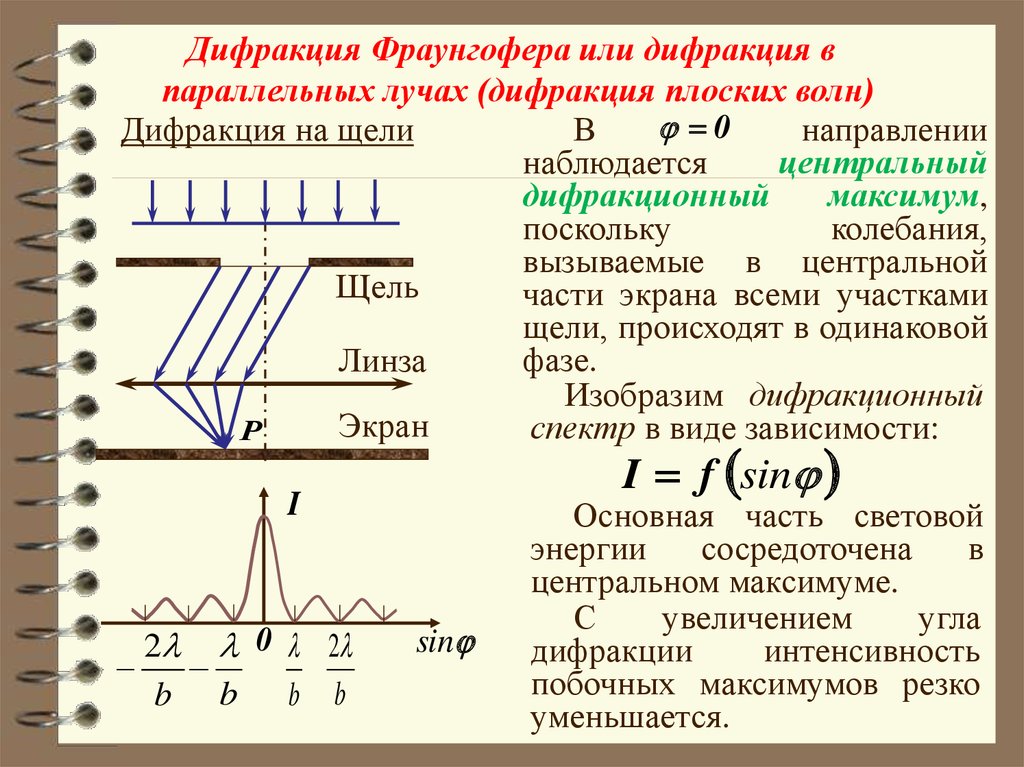
0
В
направлении
Дифракция на щели
наблюдается
центральный
дифракционный
максимум,
поскольку
колебания,
вызываемые в центральной
Щель
части экрана всеми участками
щели, происходят в одинаковой
фазе.
Линза
Изобразим дифракционный
Экран
спектр в виде зависимости:
P
I f sin
I
2 0 2
b b b b
sin
Основная часть световой
энергии
сосредоточена
в
центральном максимуме.
С
увеличением
угла
дифракции
интенсивность
побочных максимумов резко
уменьшается.

12.

Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
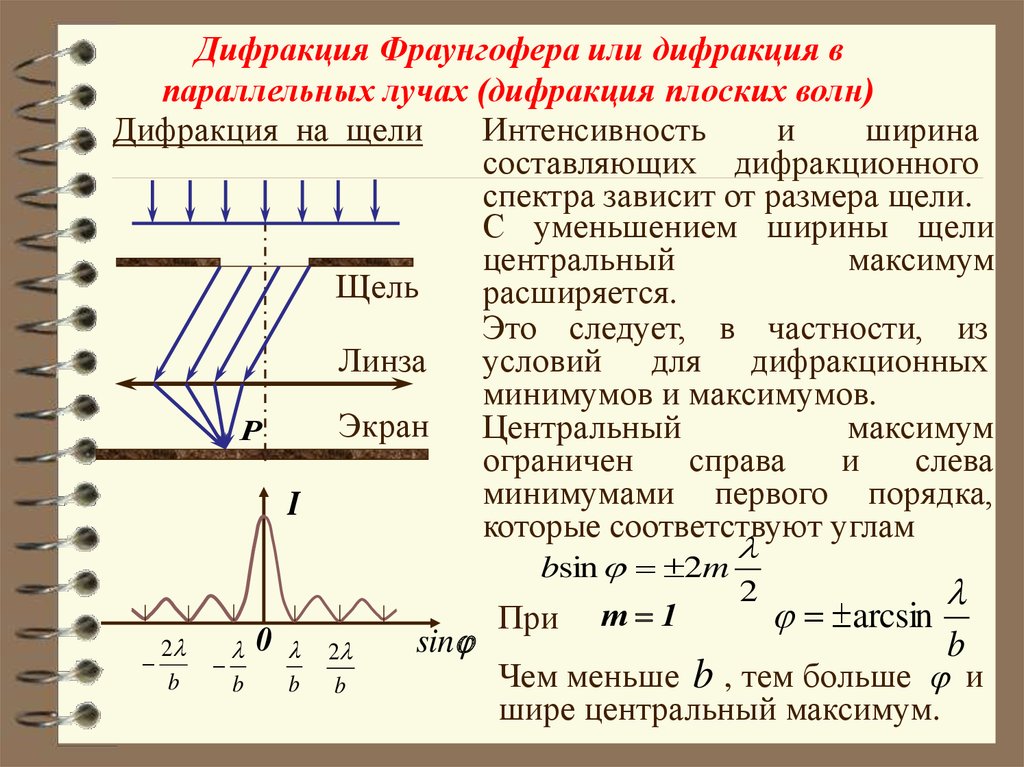
Интенсивность
и
ширина
Дифракция на щели
составляющих дифракционного
спектра зависит от размера щели.
С уменьшением ширины щели
центральный
максимум
Щель
расширяется.
Это следует, в частности, из
условий для дифракционных
Линза
минимумов и максимумов.
Экран
Центральный
максимум
P
ограничен
справа
и
слева
минимумами первого порядка,
I
которые соответствуют углам
bsin 2m
2
m
1
arcsin
При
sin
2
b
0 2
Чем меньше b , тем больше и
b
b
b b
шире центральный максимум.

13.

Дифракция Фраунгофера или дифракция в
параллельных лучах (дифракция плоских волн)
Дифракция на щели
Щель
Линза
Экран
P
I
2 0 2
b
b
b b
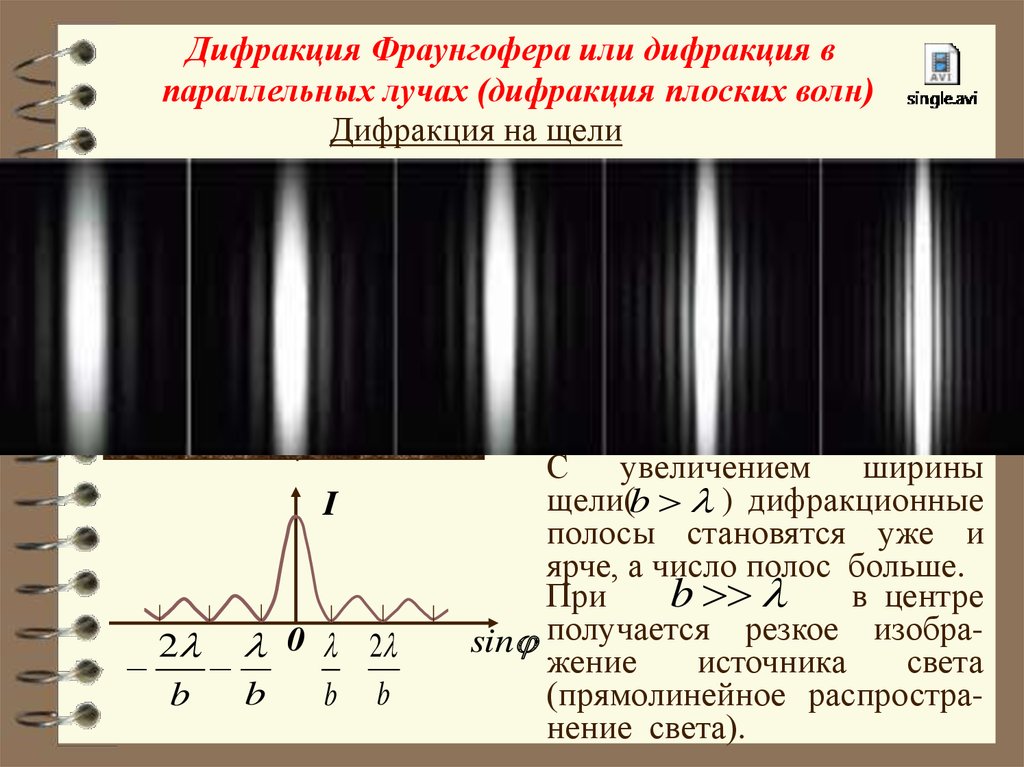
С увеличением
ширины
щели(b ) дифракционные
полосы становятся уже и
ярче, а число полос больше.
При
в центре
b
sin получается резкое изображение
источника
света
(прямолинейное распространение света).

14.

15.

16.

17.

18.

Дифракция Фраунгофера на щели.
Точная теория.
На отверстие падает плоская волна (волновой фронт – плоскость).
Известна длина волны λ, размер отверстия b и расстояние до экрана L.
Требуется Определить, как распределена интенсивность излучения по
направлениям (на экране).

19.

Дифракция Фраунгофера на щели.
Точная теория.
Каждая точка отверстия
является источником сферических волн. Рассмотрим участок
длиной dx, расположенный
внутри отверстия на расстоянии
x от края.
Волны, излучённые с отрезка
dx распространяются по всем
направлениям (-π/2 < φ < π/2).
Рассмотрим волны, распространяющиеся вдоль прямой, образующей
угол φ с перпендикуляром к преграде.
Волны, излучённые с отрезка dx, запаздывают по фазе на
k
v
kx sin ,
- волновое число (модуль волнового вектора).

20.

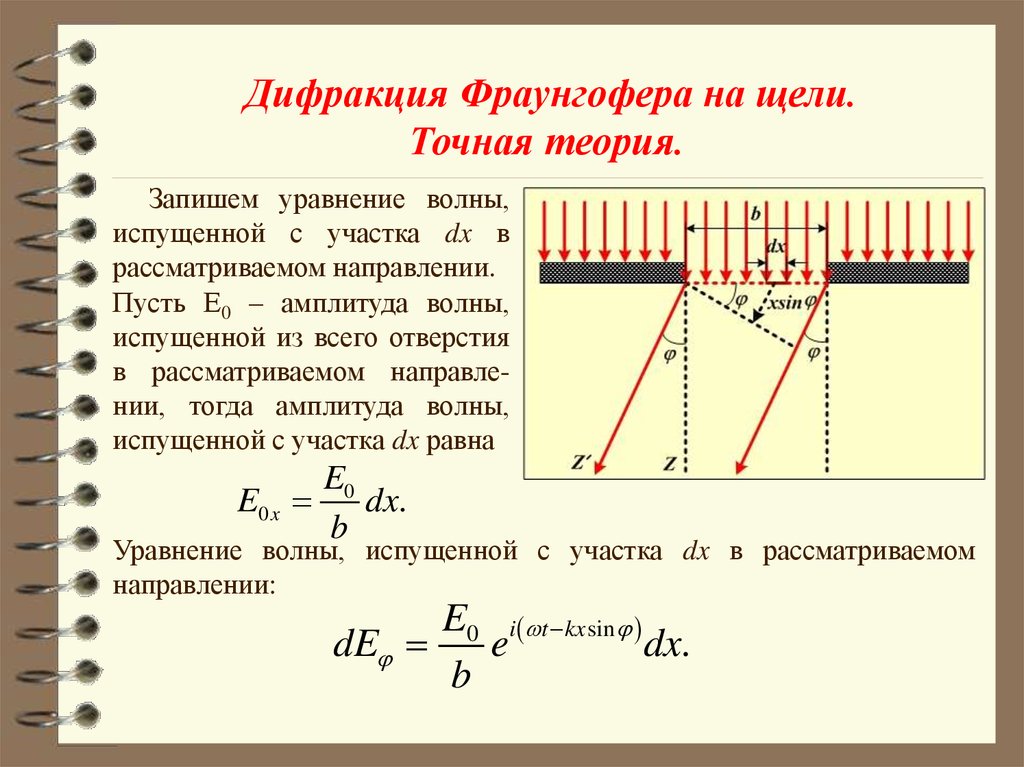
Дифракция Фраунгофера на щели.
Точная теория.
Запишем уравнение волны,
испущенной с участка dx в
рассматриваемом направлении.
Пусть Е0 – амплитуда волны,
испущенной из всего отверстия
в рассматриваемом направлении, тогда амплитуда волны,
испущенной с участка dx равна
E0
E0 x
dx.
b
Уравнение волны, испущенной с участка dx в рассматриваемом
направлении:
E0 i t kx sin
dE
e
dx.
b

21.

Дифракция Фраунгофера на щели.
Точная теория.
E0 i t kx sin
dE
e
dx.
b
Для волны, испущенной из
всего отверстия в рассматриваемом направлении.
b
E0 i t kx sin
E e
dx.
b
0
b
b
E0 i t kx sin
E0 i t ikx sin
E e
dx
e e
dx
b
b
0
0
b
ikb sin
e
1
E0 i t e
i t
.
e
E0e
ikb sin
b
ik sin 0
ikx sin

22.

Дифракция Фраунгофера на щели.
Точная теория.
E E0ei t
e ikb sin 1
.
ikb sin
Преобразуем полученное выражение к симметричной форме.
e ikb sin 1 e
ikb sin
e
b
ik sin
2
b
b
ik sin ik sin
2
2
e
b
ik sin
2
e
b
2ik sin
2
где
e
b
b
ik sin ik sin
2
2
e
ikb sin
b
ik sin
2
e
e iu e iu iu
e ,
2iu
b
u k sin .
2

23.

Дифракция Фраунгофера на щели.
Точная теория.
Итак,
e iu e iu iu sin u iu
e
e .
2iu
u
ikb sin
e
1
i t u sin u
i t
E E0e
E0e
.
ikb sin
u
где
b
u k sin .
2
Уравнение волны, испущенной из всей щели в рассматриваемом
направлении:
sin u
E E0
e
u
b
i t k sin
2
.

24.

Дифракция Фраунгофера на щели.
Точная теория.
Интенсивность излучения, испущенного из всей щели
рассматриваемом направлении определяется квадратом амплитуды
I
E E e
2
2
0
~
E
i t u
2
ср
2
2
sin u
.
u
2
sin u
I I 0
,
u
где
b
u k sin .
2
в

25.

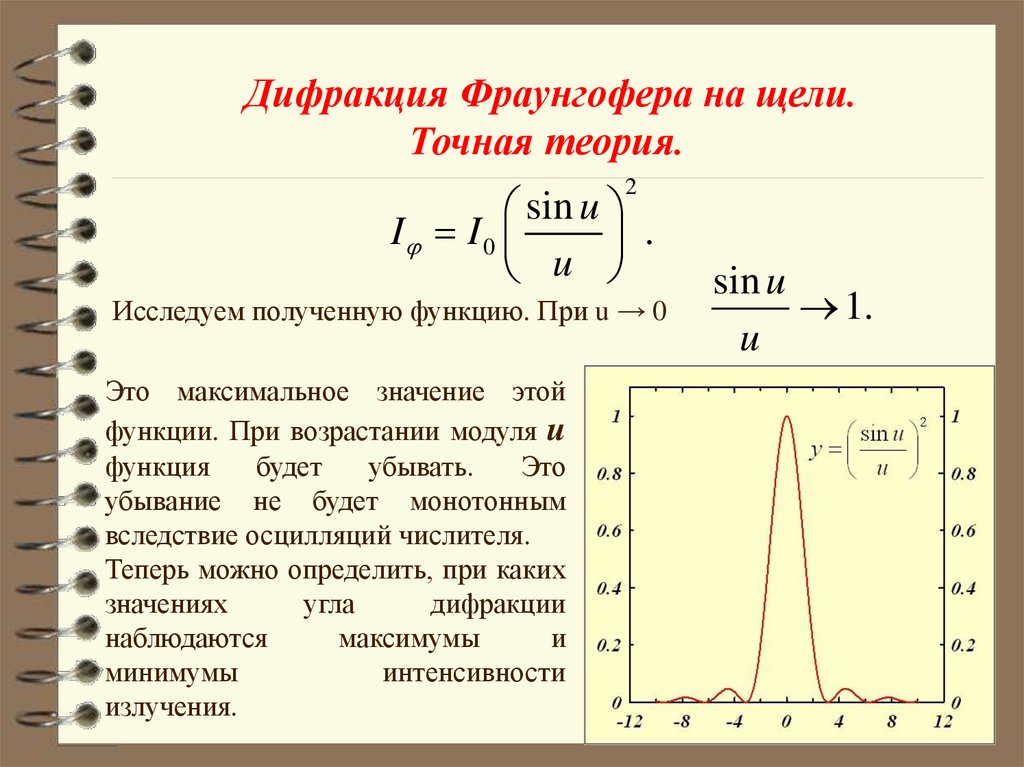
Дифракция Фраунгофера на щели.
Точная теория.
2
sin u
I I 0
.
u
Исследуем полученную функцию. При u → 0
Это максимальное значение этой
функции. При возрастании модуля u
функция
будет
убывать.
Это
убывание не будет монотонным
вследствие осцилляций числителя.
Теперь можно определить, при каких
значениях
угла
дифракции
наблюдаются
максимумы
и
минимумы
интенсивности
излучения.
sin u
1.
u

26.

Дифракция Фраунгофера на щели.
Точная теория.
b
2
u k sin ,
k
.
2
2 b
b
u
sin
sin .
2
Функция
sin u
I I 0
u
2
имеет локальные минимумы при
условии
sin u 0.
b
u m ,
sin m ,
b sin m .

27.

Дифракция Фраунгофера на щели.
Точная теория.
Функция
sin u
I I 0
u
2
имеет локальные максимумы
(кроме центрального) при условии
sin u 1.
u 2m 1 ,
2
b
sin 2m 1 ,
2
b sin 2m 1 .
2
Точный
расчёт
позволяет
определить значения интенУсловия минимумов и максимумов сивности для произвольного
совпали с полученными методом зон угла дифракции.
Френеля.

28.

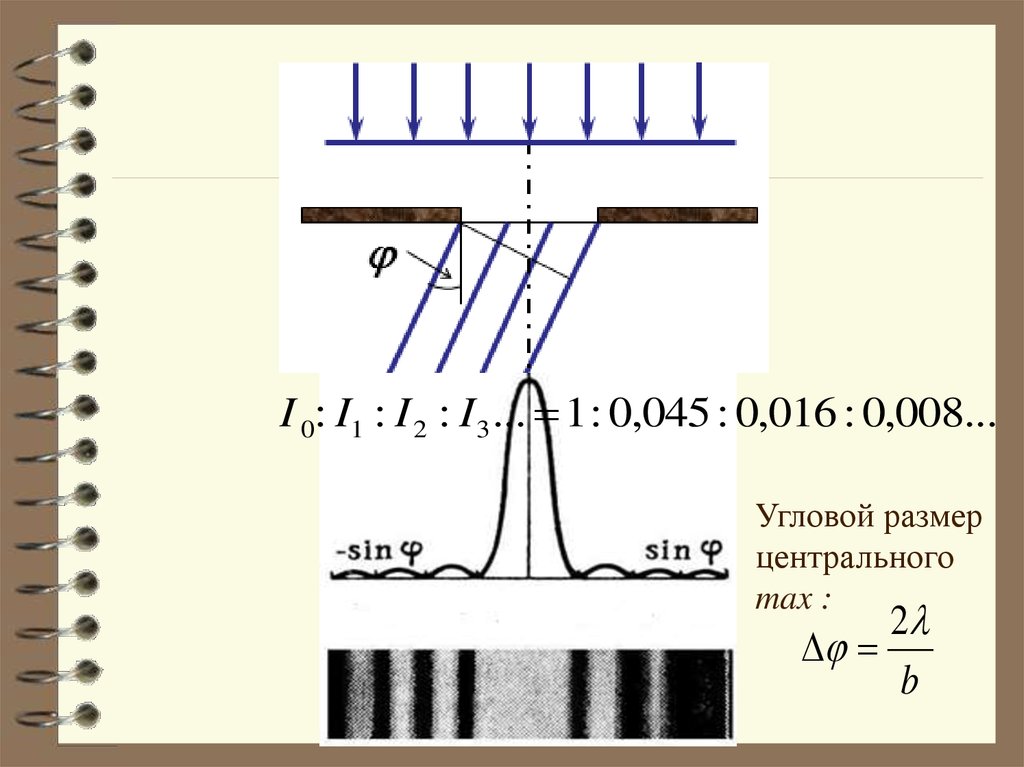
I 0: I1 : I 2 : I 3 ... 1 : 0,045 : 0,016 : 0,008...
Угловой размер
центрального
max :
2
b

29.

ЛЕКЦИЯ ЗАКОНЧЕНА!

30.

http://rutube.ru/tracks/3223274.html?v=d2e
9b72ff871d89795bb7d918e50b9b4&&bmst
art=980323