Похожие презентации:
Нелинейная парная регрессия (НПР). Лекция 11
1. Нелинейная парная регрессия (НПР)
2. План:
1. Общие сведения о нелинейныхпарных
регрессионных моделях,
виды нелинейных регрессий
2. Оценка параметров нелинейной
модели относительно фактора
3. Оценка параметров нелинейной
модели по параметрам
3. 1. Общие сведения о нелинейных парных регрессионных моделях
4.
Различают два класса нелинейныхрегрессий:
регрессии,
нелинейные
относительно
фактора,
но
линейные по параметрам
Регрессии,
нелинейные
по
параметрам
5.
Регрессии, нелинейные относительно фактора6.
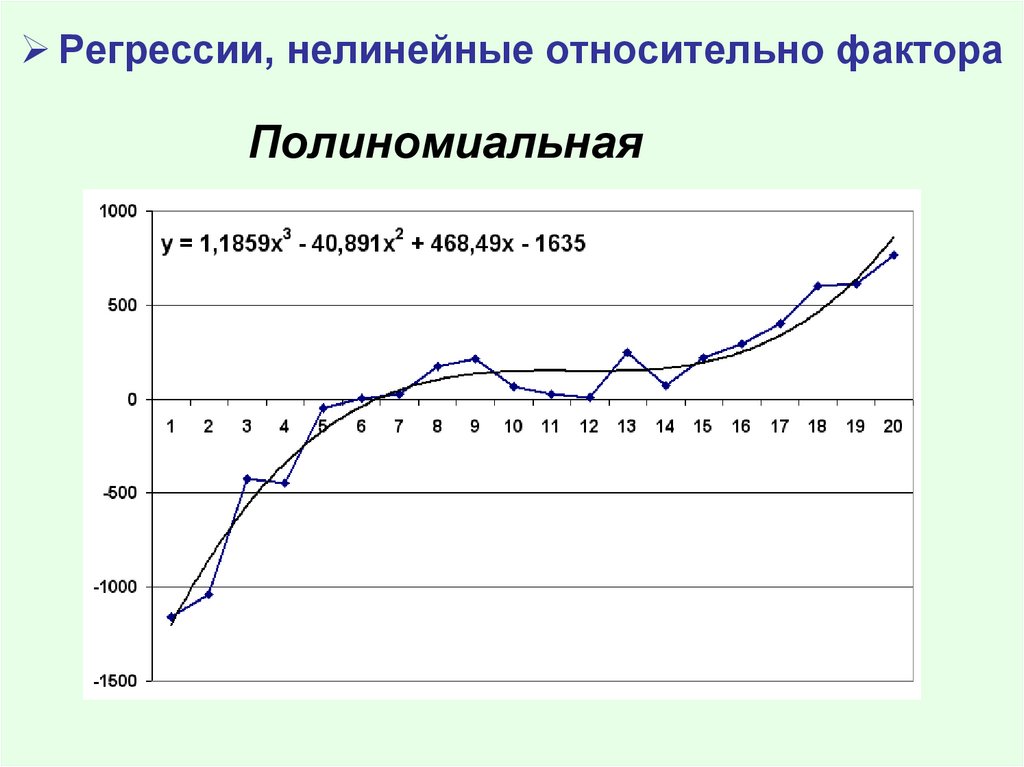
Регрессии, нелинейные относительно фактораПолиномиальная
7.
Регрессии, нелинейные относительно фактораПрименение полиномиальных моделей
Полиномом второй степени
представлены зависимости:
могут
быть
-Заработная плата физического труда от
возраста
-Урожайность
удобрений
от
количества
внесенных
-Прибыль
от
количества
каналов,
исполняющих заявки в системе массового
обслуживания и т.д.
8.
Регрессии, нелинейные относительно фактораПрименение гиперболических моделей
Классический пример: кривая Филлипса графическое
отображение
обратной
зависимости между уровнем инфляции и
уровнем безработицы.
9.
Кривая ФиллипсаХ – общий уровень безработицы (в процентах)
Y – годовой темп прироста ставки заработной платы (в процентах)
10.
Кривая ФиллипсаОлбан Уильям Филлипс (19141975) - австралийский экономист,
работавший в Англии.
Кривую Филлипса получил в 1958 г.
на основе эмпирических данных по
Англии за 1861-1957 годы
11.
Регрессии, нелинейные относительно фактораПример произвольной логарифмической модели
12.
Регрессии, нелинейные относительно фактораПрименение логарифмических моделей
Может быть использована для описания доли
расходов на товары длительного пользования
(кривая Энгеля) в зависимости от общих сумм
расходов
Эрнст Энгель (26.03.1821 - 08.12.1896) - немецкий
экономист и статистик, занимал должность директора
Прусского статистического бюро в Берлине
13.
Регрессии,параметров
нелинейные
относительно
14.
Регрессии,параметров
нелинейные
относительно
В степенной функции регрессии показатель b
является коэффициентом эластичности*
15.
Регрессии,параметров
нелинейные
относительно
Степенная
регрессия
нашла
большое
использование в производственных функциях,
в исследованиях спроса и потребления
Производственная функция валового
внутреннего продукта США по данным 19601995 гг.
Y – валовой внутренний продукт США
К – капитал
L - труд
16. 2. Оценка параметров нелинейной модели относительно фактора
17.
Полиномиальная, гиперболическая илогарифмическая модели
сводятся
к линейной форме
заменой переменных
Затем
используются
известные
соответствующие методы оценивания
параметров и проверки гипотез
18.
Полиномиальная модельНа практике используются полиномы не
более третьего порядка
Введем новые переменные:
Получили линейную модель множественной
регрессии:
19.
Гиперболическая модельПреобразование:
Получили линейную модель :
Применяя Метод Наименьших Квадратов,
получаем формулы для расчета параметров
модели:
20.
Логарифмическая модельПреобразование:
Получили линейную модель :
Применяя МНК, получаем формулы для
расчета параметров модели:
21. 3. Оценка параметров нелинейной модели по параметрам
22.
Некоторые нелинейные моделипо параметрам можно
привести к линейному виду
путем
линеаризации
23.
Примеры нелинейных моделей и ихлинеаризация
24.
Оценка параметровлинеаризованных моделей
Метод Наименьших Квадратов применяют к
преобразованному линеаризованному
уравнению
Пример: степенная регрессия
Логарифмируем:
Цель:
25.
Оценка параметровлинеаризованных моделей
Решение задачи минимизации сводится к
решению системы нормальных уравнений
26.
Оценка параметровлинеаризованных моделей
Продолжение: преобразование системы
нормальных уравнений
27.
Оценка параметровлинеаризованных моделей
Продолжение: из системы нормальных
уравнений
выражаем параметры с учетом замены
Готовые
формулы
28. Функции MATLAB для полиномиальной регрессии
Функция polyfit()Описание
p = polyfit(x,y,n) функция позволяет рассчитать
коэффициенты p полиномиальной регрессионной модели
n-й степени для выборки (x,y) методом наименьших
квадратов, где x - независимая переменная, y - зависимая
переменная.
Зависимая и независимая переменные задаются как
векторы с одинаковым числом элементов. Вектор
коэффициентов p содержит n+1 элемент, расположенных
по убыванию степени независимой переменной согласно
формуле:
p(x) = p1 xn + p2 xn-1 + … + pn x + pn+1
29. Продолжение
[p,S] = polyfit(x,y,n) функция возвращает коэффициенты pполиномиальной регрессионной модели n-й степени и
матрицу S для выборки (x,y).
Матрица S используется в качестве входного
аргумента
функции
polyconf
для
расчета
границ
доверительного интервала значений полиномиальной
регрессионной модели в заданных точках.
Если отклонения значений зависимой переменной y
от регрессионной модели независимы и распределены по
нормальному закону с постоянной дисперсией, границы
доверительного интервала, полученные polyconf , включают
как минимум 50% рассчитанных значений.
30. Продолжение
Функция polyval()Описание:
• Функция y = polyval(p, s),
где p = [p1 p2 ... pn pn+1] - вектор коэффициентов полинома
p(x) = p1xn + p2xn-1 + ... + pnx + pn+1,
вычисляет значение этого полинома в точке x = s.
• Функция Y = polyval(p, S), где S - одномерный или
двумерный массив, вычисляет значение этого полинома
для каждого элемента массива
31. Продолжение
Функция polyconf()Описание:
[Y,DELTA] = polyconf(p,X,S) функция позволяет рассчитать значения
зависимой
переменой
Y
однофакторной
регрессионной
полиномиальной модели произвольного порядка в заданных точках X.
Коэффициенты регрессионной модели задаются вектором р.
Вектор
коэффициентов
p
содержит
n+1
элемент,
расположенных по убыванию степени независимой переменной, n –
порядок полинома.
Входной аргумент S рассчитывается с использованием
функции polyfit.
Результаты расчета значений зависимой переменной могут
быть представлены как Y±DELTA, где DELTA соответствует 95%
доверительному интервалу.
При расчете DELTA предполагается, что отклонения значений
зависимой переменной y от регрессионной модели независимы и
распределены по нормальному закону с постоянной дисперсией.






























 Математика
Математика








