Похожие презентации:
Степень с натуральным показателем
1. Степень с натуральным показателем
Алгебра7 класс2. Этапы урока:
12
3
4
5
Тема урока
Цель урока
Устный счёт
Изучение нового материала.
Формирование умений и навыков
3. Устный счёт Вычислите: 32 =* , 33 = *, (-3)3 =*, 22 =* , *3 = 8, (*)2 = 4, (-2)3 = *, *2= 16, 43= *, (*)3= -64, 0,52 = *; 0,53
Устный счётВычислите:
32 =* , 33 = *, (-3)3 =*,
2
2
=* ,
3
*
= 8,
(*)2 = 4, (-2)3 = *,
*2= 16, 43= *, (*)3= -64,
0,52 = *; 0,53 = *
4. Рассмотрим краткость записи суммы одинаковых слагаемых. 3+3+3+3+3 = 5∙3 = 15 а+а+а+а+а+а+а = 7∙а х+х+х+…+х = n∙x
Рассмотрим краткость записи суммыодинаковых слагаемых.
3+3+3+3+3 = 5∙3 = 15
а+а+а+а+а+а+а = 7∙а
х+х+х+…+х = n∙x
5. Записи произведения одинаковых множителей 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 39 1,5 ∙ 1,5 ∙ 1,5 ∙ 1,5 ∙ 1,5 ∙ 1,5 = 1,56 (-2с)
∙(-2с) ∙ (-2с) ∙ (-2с) ∙(-2с) = (-2с)5(х+y) ∙ (х+y) ∙ (х+y) ∙ (х+y) = (х+y)4
6. Выражение аn называют степенью, число a – основанием степени, число n - показателем степени.
nа
Выражение
называют степенью, число a –
основанием степени, число n показателем степени.
7. Читаем: - а в n-ой степени; - a в квадрате, или а во второй степени; - a в кубе, или а в третьей степени.
Читаем:- а в n-ой степени;
- a в квадрате, или а во
второй степени;
- a в кубе, или а в третьей
степени.
8.
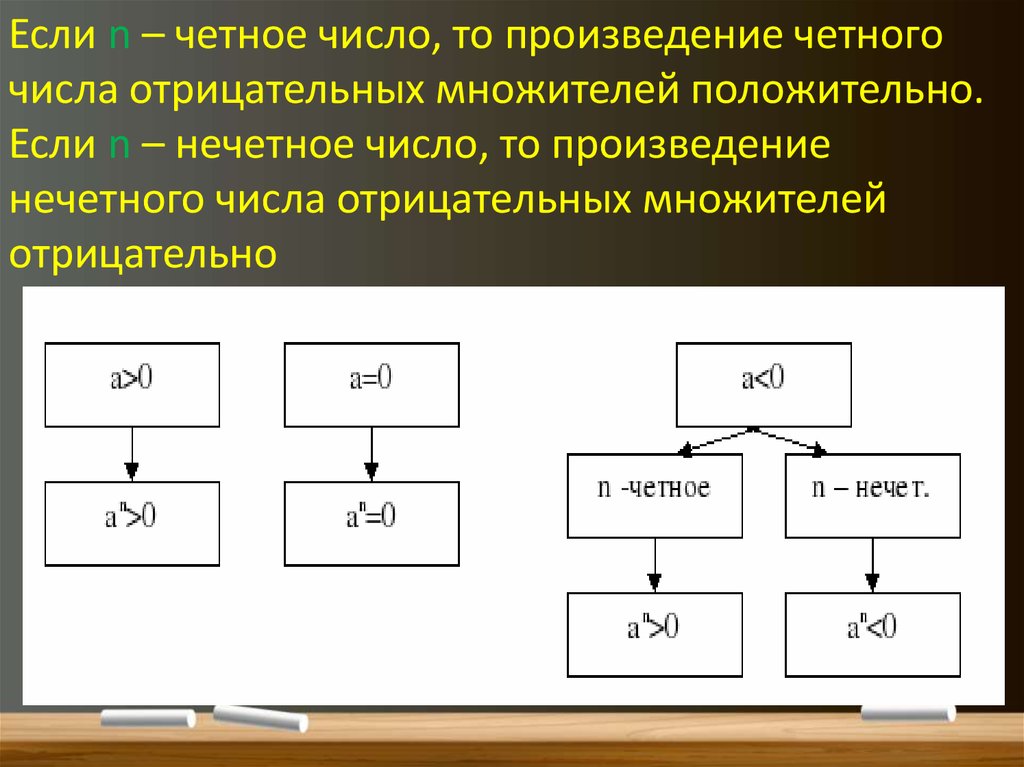
Если n – четное число, то произведение четногочисла отрицательных множителей положительно.
Если n – нечетное число, то произведение
нечетного числа отрицательных множителей
отрицательно
9.
Упр. № 157а
2 -2 10
2
а
4 4 100 100 0,01 0,01
а3 8 -8
а4
16 16
-10
0,1
-0,1
1/2 -1/2
1/4 1/4
1000 -1000 0,001 -0,001
1/8
-1/8
10000 10000
1/16
1/16
0,0001 0,0001
10. Закрепление знаний учащихся: Что называется степенью с натуральным показателем? Что мы называем степенью, основанием степени,
показателем степени?Что называется степенью с показателем 1?
Какие числа можно возвести в степень?
Что получается при возведении в степень
положительного числа?
Что получается при возведении в степень нуля?
Что получается при возведении в степень
отрицательного числа, если степень чётное число?
Что получается при возведении в степень
отрицательного числа, если степень нечётное число?
11. Домашнее задание: §5, выучить определения, № 156, 158,161 стр. 38-39
Домашнее задание:§5, выучить определения,
№ 156, 158,161 стр. 38-39
12. Рефлексия Закончим наш урок словами известного русского учёного Михаила Васильевича Ломоносова. «Пусть кто-нибудь попробует
вычеркнутьиз математики степени, и он увидит, что
без них далеко не уедешь»











 Математика
Математика








