Похожие презентации:
Степень с натуральным и целым показателем
1. Степень с натуральным и целым показателем
2. Степень с натуральным показателем
an= a∙a∙…∙an
a n a
a
...
a
n раз
Степенью числа a с
натуральным
показателем n
называется
произведение n
множителей, каждый
из которых равен a.
3. Свойства степени
pq
p q
a a a
a a a
a p a
ab a b
a a
b b
p
p q
q
q
p
p
pq
p
p
p
p
4. Определение степени с нулевым показателем
Степень числа a, неравного нулю, с
нулевым
показателем равна
единице
a 1
0
5.
В чём смысл этойзаписи?
6. Определение степени с целым отрицательным показателем
Если а 0 и n , тоa
n
1
n
a
7. Вычислите:
23
3 = 9 ; 0,01 =0,001
=
2
22
4 = 16; ;(-6)
(-6) == 36
°
23
23
5 = 1 ;; 11 ==1
°°
6
О = 0 ; 00== 1
8. Представьте число в виде произведения двух одинаковых множителей двумя способами:
251/81
1/25
2
1/а
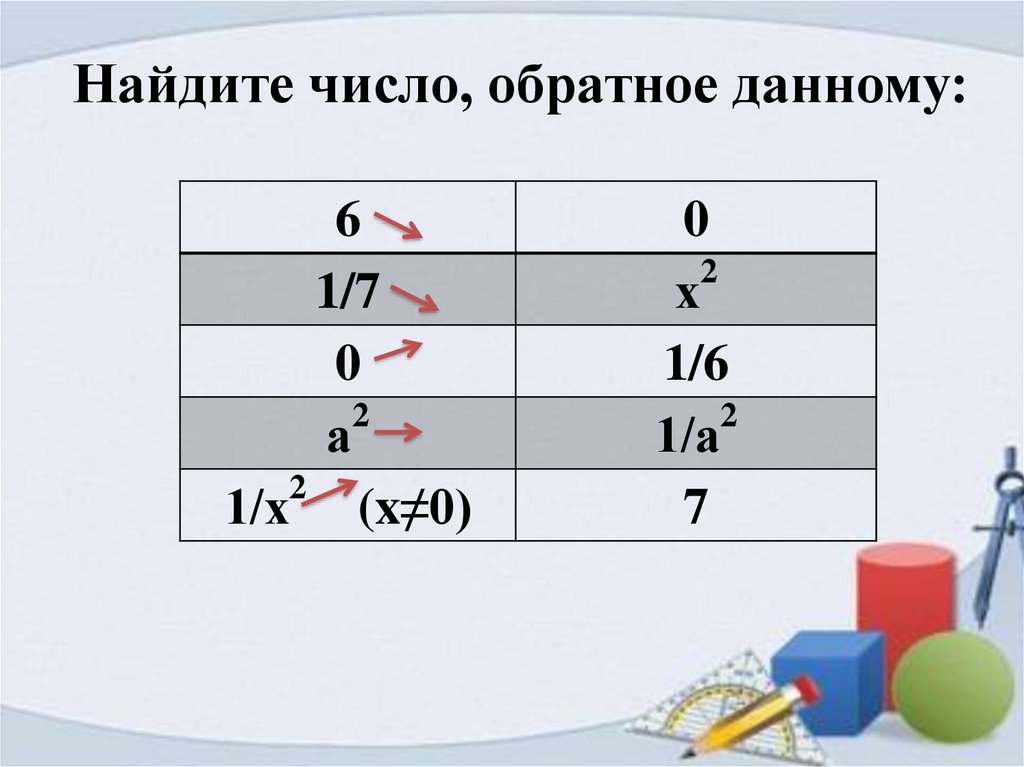
9. Найдите число, обратное данному:
61/7
0
2
а
2
1/х (x≠0)
0
2
х
1/6
2
1/а
7
10. Взгляните на число 10-24 Как вы думаете, это положительное или отрицательное число?
Вписать такие основания ипоказатели степени, чтобы
получились верные равенства
4
-6
а ∙а- =а-2
a)
-3
-2
в) a ∙ a- =a-5
4 -2
д) (a-) =a-8
7
б)
∙ a- =a5
8
г) а- ∙ а-3 = а5
5 -5 =15-5
е) 3-5 ∙ __
a-2
11. 1) Уловите закономерность и продолжите ряд чисел
1. Выполнить действияа-11
a) а-6∙а∙а-4 =___;
а8
в) (a-4)-2 =___;
a-8
-3
-5
а
a =___;
б)
:
1
г) а-15: а-15 = ___;
-2
-3
а
е) а ∙а=___.
д) (2a3)-3 =___;
2. Вписать недостающий множитель
-5
-5
4а
3а ∙ ___
=12а-10;
а)
-2b-4 ∙4а-7b=24а-9b-3;
в) 6а
____
8
4a
б)
___ =32а2;
4b-2)=6а-1b6.
-2a-5b8
г) _____∙(-3а
(2а-2)3 ∙
12. 2) Представим каждое из этих чисел в виде степени числа 10:
Представьте выражение в видестепени
1
2
4
( x3 a y)
1
y6
13.
Упростите3 1 3 4 42
x 8 x 6
((xax b
)
: x)
14.
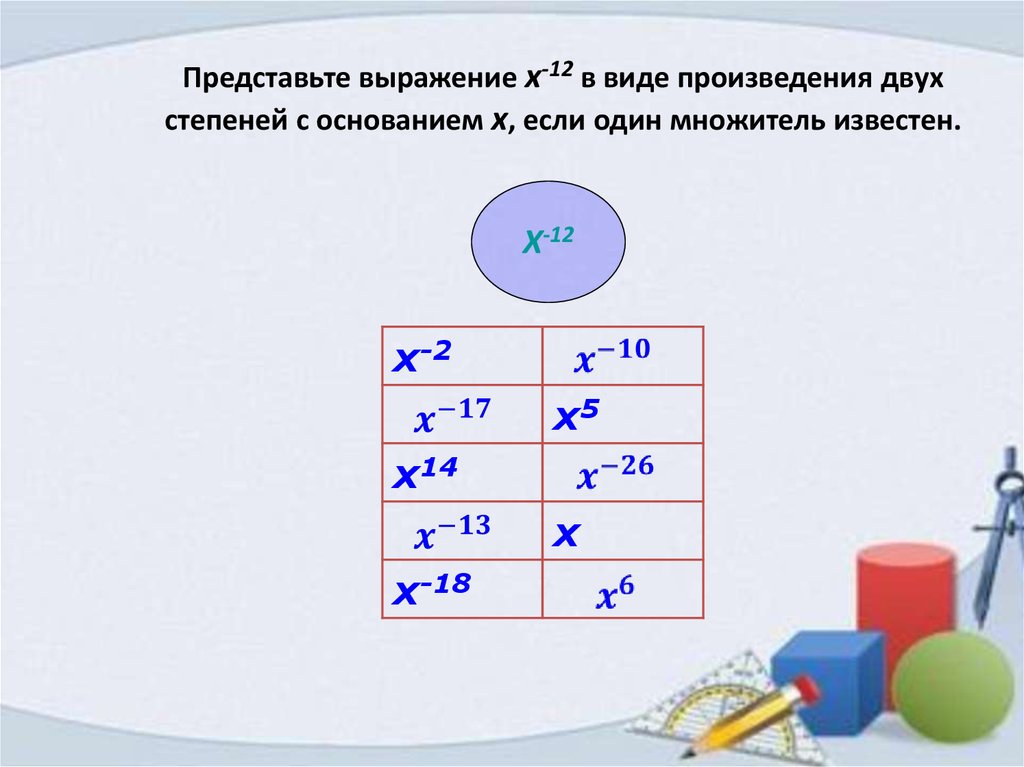
Представьте выражение x-12 в виде произведения двухстепеней с основанием x, если один множитель известен.
X-12
x-2
x5
x14
x
x-18
15.
Вычислите10
2 3
5
12
32
(
7
)
2 2 :2
3 4 5
7
5 5
18
(0,2) 4
16.
Расположите в порядке убывания0,2-6; 0,20; 0,2; (0,2)-4; 0,23
17. а) 3а-5 ∙ ___ =12а-10; б) (2а-2)3 ∙ ___ =32а2; в) ____ ∙4а-7b=24а-9b-3; г) _____∙(-3а4b-2)=6а-1b6.
При каких значениях х верноравенство
1
1
x
21x x
27
8
,01
3 2 0100
10
16
xx
5 x 625
18. Представьте выражение в виде степени
19. Упростите
20. Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен.
Корнем n – ой ст епени из числа а называет ся т акоечисло, n – ая ст епень кот орого равна а.
n
a
подкоренное выражение
показатель корня
21. Вычислите
22. Расположите в порядке убывания
23. При каких значениях х верно равенство
24.
25.
26.
27.
Корень нечетной степени из отрицательного числа можновыразить через арифметический корень.
28.
Свойства корнейab a b
n
n
n
a
n
a
n
n
a
a
n ,b 0
b
b
n k
a
n k
a,k 0
n k
n
k
a ,k 0
k
a
n
k
0 a b, a b
n
n
29.
Покажем на примерах, как используются свойства корней и рациональных степеней ввычислениях.
• Пример 1. Вычислить
30.
Решение. 1) Упростим сначала первую часть выражения.n
n
n
Используя свойство ab a b , получим
.
Теперь применим свойстваn k a n k a , k 0 и n a n k a k , k 0 :
n
n
n
Применим теперь свойство ab a b :
В итоге мы получили:
2) По свойству
n
a n k a k , k 0 :
Подставим результаты вычислений из 1) и 2) в выражение
Здесь мы использовали свойства ab a b и a
арифметических корней.
n
Ответ: 2.
n
n
n
k
a
n
k
31.
32.
33.
34.
35. Свойства корней
36. Покажем на примерах, как используются свойства корней и рациональных степеней в вычислениях.
37.
Степень с основанием, равным нулю,определяется только для положительного
дробного показателя:
38.
Для отрицательных оснований степеньс дробным показателем не рассматривается.
39.
Свойства степени с целымпоказателем справедливы и для
степени
с любым рациональным показателем.
40.
41.
42.
Решение:• Упростим выражение:
Ответ: 50.
43.
Решение:• Разложим на множители числитель и знаменатель дроби:









































 Математика
Математика








