Похожие презентации:
Введение в динамику механической системы
1.
Новосибирский Государственный Архитектурно-СтроительныйУниверситет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 3.
ВВЕДЕНИЕ В ДИНАМИКУ
МЕХАНИЧЕСКОЙ СИСТЕМЫ
Кафедра теоретической механики
2. План лекции
Введение1 Механическая система
2 ДУ движения механической системы
3 Меры движения
4 Внешние и внутренние силы
5 Масса системы, центр масс, момент инерции
относительно оси
6 Моменты инерции относительно
параллельных осей
7 Момент инерции относительно произвольной
оси
Заключение
3. На предыдущих лекциях
Изучили динамику материальной точки. Основнойзакон движения:
ma F ; F Fk равнодействующая
Система отсчета инерциальная
В качестве примера подробно познакомились с
колебательным движением точки
4. Цель лекции
Определить понятия механическойсистемы и основных характеристик,
необходимых для изучения ее
движения
5. Введение
Напомним: В качестве тел мы изучаем 1) точки,2) абсолютно твердые тела и 3) конструкции,
состоящие из 1) и 2)
Динамику точки мы изучили
Переходим к изучению механических систем:
Механическая система:
- система материальных точек
- твердое тело
- система твердых тел
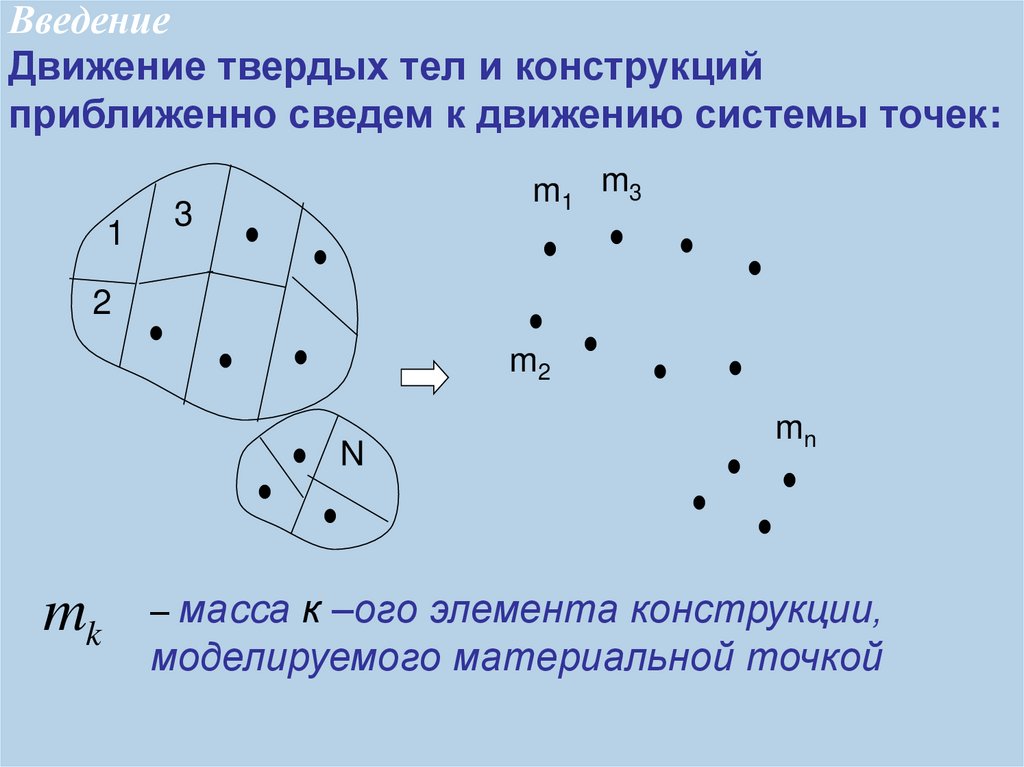
6. Введение
Движение твердых тел и конструкцийприближенно сведем к движению системы точек:
1
m1 m3
3
2
m2
N
mk
mn
– маccа к –ого элемента конструкции,
моделируемого материальной точкой
7. Алгоритм редукции системы твердых тел к системе из n точек
ВведениеАлгоритм редукции системы твердых тел
к системе из n точек
1
Имеем систему из твердых тел
2
Разобьем её на n частей (n – большое число)
3
Заменим каждую k-ю часть системы на
материальную точку с массой равной массе
этого элемента
4
Получим систему из n материальных точек с
массами
m , m , m ...m
1
2
3
n
8. ДУ движения механической системы
Рассмотрим движение механической системыв инерциальной системе координат.
Запишем второй закон Ньютона для k-й точки
2
mk
d rk
dt
2
Fk
(1)
Fk - равнодействующая всех сил
rk
(активных и реакций связей)
- радиус-вектор
mk x k Fkx
m k y k Fky
k 1,..., n
mk z k Fkz
(2)
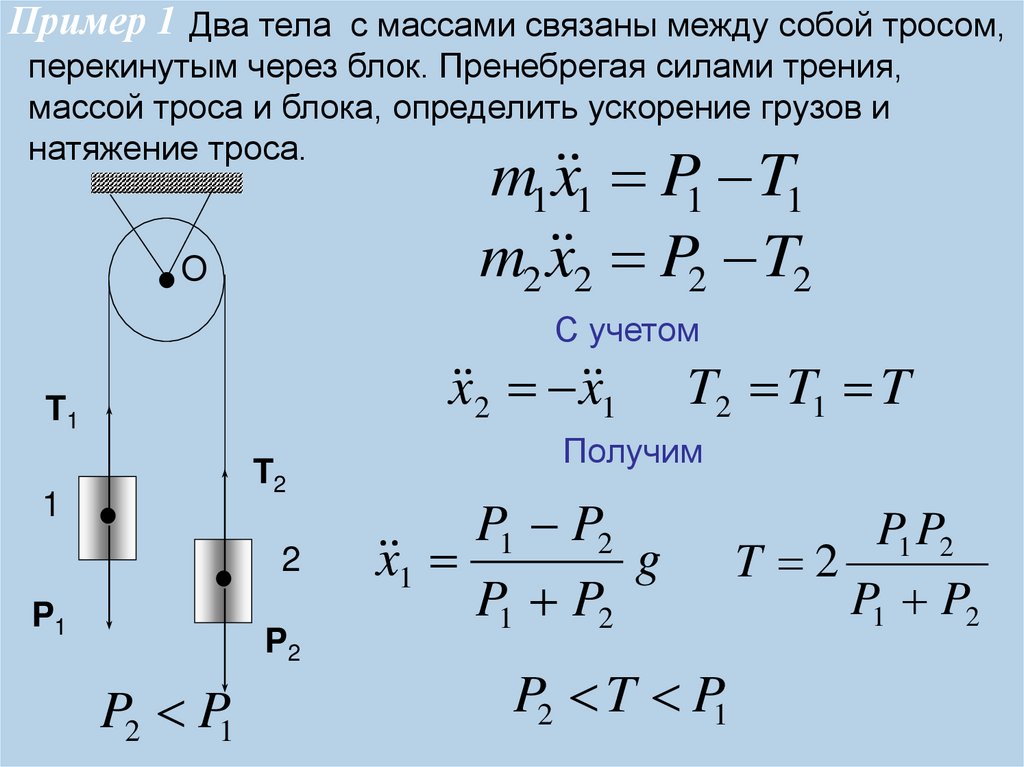
9. Пример 1
Два тела с массами связаны между собой тросом,перекинутым через блок. Пренебрегая силами трения,
массой троса и блока, определить ускорение грузов и
натяжение троса.
m1 x 1 P1 T1
m2 x 2 P2 T2
O
С учетом
x 2 x 1
T1
T2
1
2
P1
P2
P2 P1
T2 T1 T
Получим
P1 P2
x 1
g
P1 P2
P2 T P1
P1 P2
T 2
P1 P2
10. Пример 2 (задача двух тел)
Две точки M 1 и M 2 с массами m1 и m2 движутсяпод действием сил ньютоновского притяжения. Составить ДУ
их движения.
Oxyz инерциальная,
r r2 r1
z
M1
F1
F2
r1
F1 F2 fm1m2 / r
M2
r2
O
y
x
2
f гравитационная
постоянная
2
F1 F2 ( fm1m2 / r )( r / r )
2
2
d r
m1m2
d r
m1m2
m1 2 f
r ; m2 2 f
r
3
3
dt
r
dt
r
11. ДУ движения механической системы
Основные трудности при решении ДУ:1. Как правило, мы не знаем полностью всех сил
(силы реакции связей и силы взаимодействия элементов
конструкции между собой, которые чаще всего заранее
неизвестны)
2. Большое число уравнений (10, 100, 100 000 000 …)
Расчет требует применения мощных
компьютеров, разработки численных методов
решения ДУ и изучения свойств материалов
самой конструкции
Другой путь: Вводят характеристики движения
(меры движения) и по их поведению судят о
движении системы в целом.
Примеры: работа военкомата, конкурс красавиц.
12. МЕРЫ ДВИЖЕНИЯ механической системы:
1 – центр масс системыrC ( mk rk ) / M
2 – количество движения (импульс) системы
Q mk v k
3 – момент количества движения
(момент импульса) системы
KO M O (mk v k )
4 – кинетическая энергия системы
1
2
T ( mk v k )
2
13. МЕРЫ ДВИЖЕНИЯ механической системы:
Соответственно, будут получены и четыретеоремы о движении этих характеристик:
1)Теорема о движении центра масс
2)Теорема об изменении количества движения
3) Теорема об изменении момента количества
движения
4) Теорема об изменении кинетической энергии
14. Внешние и внутренние силы
В статике мы рассматривали равновесие систем тели уже разделяли силы на внешние и внутренние
e
Внешними по отношению к данной
механической системе называются силы,
действующие на точки этой системы со
стороны тел не входящих в нее.
i
Внутренними называются силы
взаимодействия между точками
данной механической системы.
Пример: Солнечная система:
e
Внешние силы - силы притяжения звезд
i
Внутренние силы - силы взаимодействия между
отдельными ее планетами
15. Два свойства внутренних сил
По 3-му закону Ньютона (о равенстве действия ипротиводействия) каждой внутренней силе
соответствует другая внутренняя сила, равная ей
по модулю и противоположная по направлению.
Из этого следуют два свойства внутренних сил
1. Главный вектор внутренних сил системы равен нулю
i
F
k 0
(3)
k
2. Главный момент внутренних сил системы
относительно любого центра равен нулю
M (F ) 0
0
k
i
k
(4)
16. Масса системы, центр масс
Масса материальной точки полностью характеризуетмеру инерции точки. Согласно 2-му закону
Ньютона, движение точки при заданной массе
полностью определяется заданными силами, действующими
на точку и ее начальными условиями.
В случае механической системы состоящей из N
точек масса системы M уже не определяют полностью
меру инерции системы.
Например, вращение фигуриста будет
происходить с разной угловой скоростью, в зависимости
от того, прижаты или расставлены у него руки.
То есть движение механической системы зависит еще и от
распределения масс, определяемое координатами ее
отдельных точек. Поэтому наряду с массой системы
еще вводят понятия центра масс и момента инерции
относительно оси.
17. Центр масс
Центром масс механической системы называетсягеометрическая точка с координатами
x c ( m k x k ) / M
k
y c ( m k y k ) / M
(5)
k
z c ( m k z k ) / M
k
M mk - масса системы
mk - масса k-й точки системы
xk , yk , zk - координаты k-й точки системы
18. Центр масс и центр тяжести
Центр массВ однородном поле силы тяжести, для которого,
вес любой точки пропорционален массе
g const
центр масс совпадает с центром тяжести.
Вместе с тем, в отличие от центра тяжести,
понятие центра масс сохраняет смысл и для
систем, находящихся в любом силовом поле.
19. Момент инерции относительно оси
Моментом инерции тела (системы) относительноданной оси OZ называется величина, равная сумме
произведений масс всех точек тела (системы) на
квадраты их расстояний до этой оси
J z mk h
2
k
(6)
k
J z - осевой момент инерции
hk - расстояние от точки до оси
Осевой момент инерции для вращающегося
тела играет такую же роль, что масса при его
поступательном движении
20. Моменты инерции относительно осей x,y,z
Выразим расстояния точек до осей через их координатыJ z mk h
hk
xk , yk , zk
h x y
2
k
2
k
2
k
2
k
J z mk ( x y )
k
2
k
z
2
k
k
В результате получим
hk
J x mk ( y z )
2
k
mk
zk
2
k
k
y
O
J y mk ( x k2 z k2 )
k
yk
x
xk
J z mk ( x y )
2
k
k
2
k
(7)
21. Радиус инерции тела
Jz M2
z
(8)
радиус инерции
z геометрически равен расстоянию от
оси той точки, в которой нужно сосредоточить всю массу
тела (системы), чтобы момент инерции одной этой точки
был равен моменту инерции всего тела (системы)
Момент инерции сплошного тела
Разобъем тело на элементарные части, в пределе
сумма обратится в интеграл
J z mk h
dm dV
2
k
k
J z h dm h dV
2
(M )
2
(V )
(9)
22. Пример 1
Тонкий однородный стерженьO
h x
dm dx
x
__________
dx
l
M
z
l
1 M / l
J z Ml / 3 M
2
x
2
z
z l / 3 0.58l
M
l
J z x dm 1 x dx 1l / 3 Ml / 3
2
0
2
0
3
2
23. Пример 2
Тонкий однородный дискM
R
2 rdr
dm 2 rdr
2
M / R
r
dr
R
z
J z MR 2 / 2 M z2
z 0.705R
J z h dm
2
(M )
R
R
0
0
r 2 2 rdr 2 r 3 dr R 4 / 2 MR 2 / 2
24. Теорема Гюйгенса
z1J z m k ( x k2 y k2 )
d
z
C
k
J cz1 mk ( x y )
y1
2
1k
2
1k
k
O
x, x1
y
xk x1k d , yk y1k
С – центр масс
x x 2 x1k d d
2
k
2
1k
J z mk ( x12k y12k ) ( mk )d 2 2( mk x1k )d
k
mk x1k Mx1c 0
k
k
k
J z J cz1 Md
2
2
25. Теорема Гюйгенса
J z J cz1 Md2
(10)
Момент инерции тела относительно данной оси
равен моменту инерции относительно оси, ей
параллельной и проходящей через центр масс
тела, сложенному с произведением его массы на
квадрат расстояния между осями
J cz1
момент инерции относительно
центра масс тела
Jz
момент инерции тела
относительно произвольной
d
расстояние между осями
J z2 J z1 M (d d )
2
2
2
1
26. Момент инерции относительно произвольной оси
J l mk hk2l
k
hk
z
Mk
C
γ
rk2 x k2 y k2 z k2
rk
α
O
β
hk2 rk2 OC k2
y
xk il xk cos ,
yk jl yk cos ,
z k kl z k cos
x
J l (( xk2 yk2 zk2 ) ( xk cos yk cos zk cos ) 2 )mk
k
l - произвольная ось с углами , ,
27. Момент инерции относительно произвольной оси
J l cos mk ( y z )2
2
k
2
k
k
cos mk ( x z )
2
2
k
2
k
k
cos mk ( x y )
2
2
k
2
k
k
2 cos cos mk yk z k
k
2 cos cos mk xk z k
k
2 cos cos mk xk yk
k
(11)
28. Осевые и центробежные моменты инерции
Осевые моменты инерции:2
2
2
2
J
m
(
x
y
J
m
(
x
z
)
;
J x mk ( y z ); y k k k
k k k)
z
2
k
2
k
k
k
k
Центробежные моменты инерции:
J yz mk yk zk ; J xz mk xk zk ; J xy mk x k y k
k
k
k
Момент инерции относительно произвольной оси l:
J l J x cos J y cos J z cos
2
2
2
(12)
2 J yz cos cos 2 J xz cos cos 2 J xy cos cos
29. Осевые и центробежные моменты инерции
В отличие от осевых, центробежные моментыинерции могут быть как положительные, так и
отрицательные и, в частности, при
определенном выборе осей обращаться в нули
Осевой момент инерции характеризует меру инертности
тела при его вращении вокруг соответствующей оси
Центробежные моменты инерции характеризуют
несимметричность распределения масс тела относительно
координатных осей или плоскостей
30. Заключение
1. Дано определение механической системы2. Приведены ДУ ее движения
3. Определены меры движения: центр масс,
количество движения, момент количества
движения, кинетическая энергия
4. Определены внешние и внутренние силы,
действующим на систему
5. Показано, что сумма внутренних сил и сумма их
моментов равны нулю
6. Дано определение массы, центра масс и
момента инерции относительно оси
7. Доказана Теорема Гюйгенса о связи между
моментами инерции относительно
параллельных осей
31. Вопросы для самоконтроля
Каким образом задача о движении произвольноймеханической
системы
(конструкции)
приближенно
сводится к задаче о движении конечного числа
материальных точек?
2. материальных
Какие основные точек,
сложности
решения системы
ДУ
описывающих
движение
движения
материальной системы? Какой другой путь приближенного
описания движения механических систем?
3. Какие силы называются внутренними, а какие внешними
для выбранной механической системы?
4. Какими свойствами обладают внутренние силы,
действующие на элементы механической системы?
5. Что называют центром масс системы? Как определяются
его координаты?
6. Какая связь между центром масс и центром тяжести
системы?
7. Как определяется момент инерции относительно оси? Что
такое радиус инерции?
1.
32. Вопросы для самоконтроля
8. Относительно какой из параллельных осей момент инерциибудет наименьшим?
9. Какова зависимость между моментами инерции
относительно двух параллельных осей?
10. Как определяются центробежные моменты инерции и что
они характеризуют?
11. Как определить момент инерции относительно
произвольной оси, проходящей через начало системы
Oxyz
координат
33. Тема следующей лекции
Теорема о движении центрамасс и об изменении
количества движения
системы
























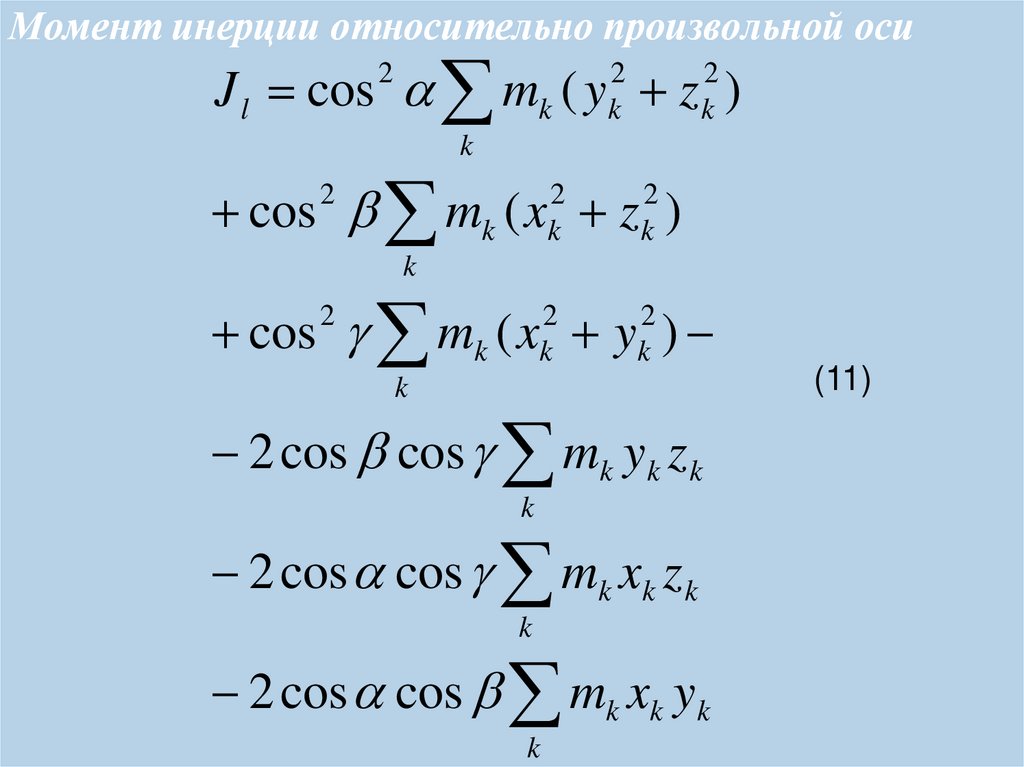







 Физика
Физика








