Задачи по геометрии

1.

Сеть творческих учителей. Сообщество учителей математики.
Творческая группа
Мастерская. Мультимедийные презентации для уроков математики.

2.

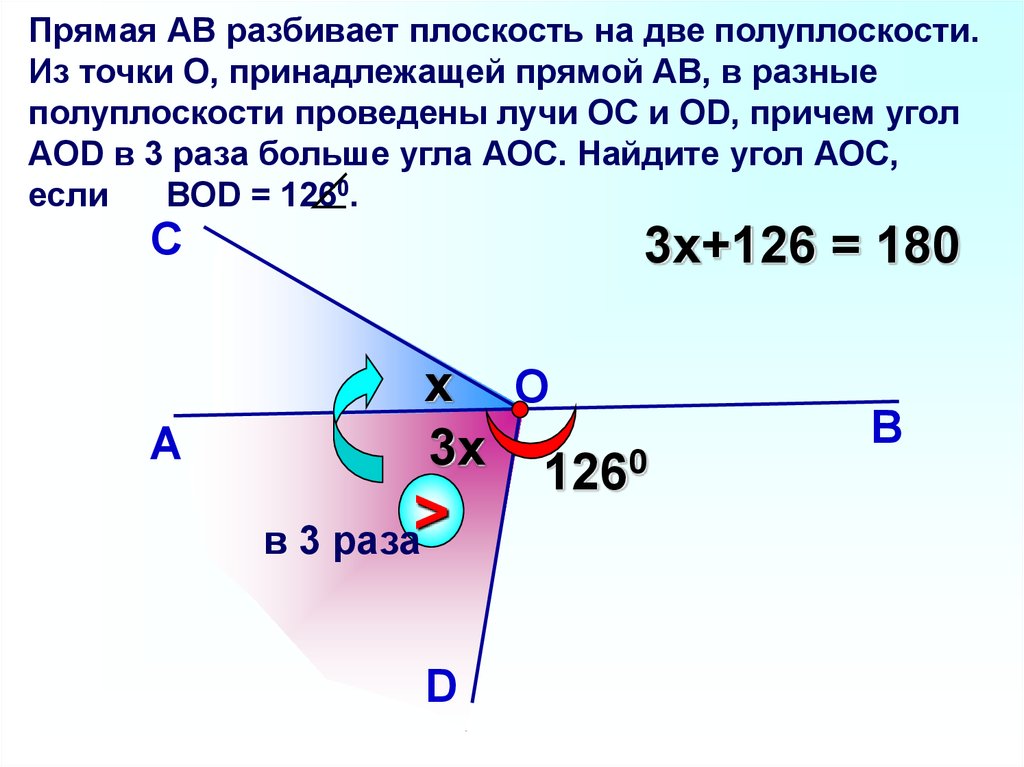
Прямая АВ разбивает плоскость на две полуплоскости.
Из точки О, принадлежащей прямой АВ, в разные
полуплоскости проведены лучи ОС и ОD, причем угол
АОD в 3 раза больше угла АОС. Найдите угол АОС,
если
ВОD = 126
0.
С
А
3x+126 = 180
x O
3x 1260
>
в 3 раза
D
В

3.

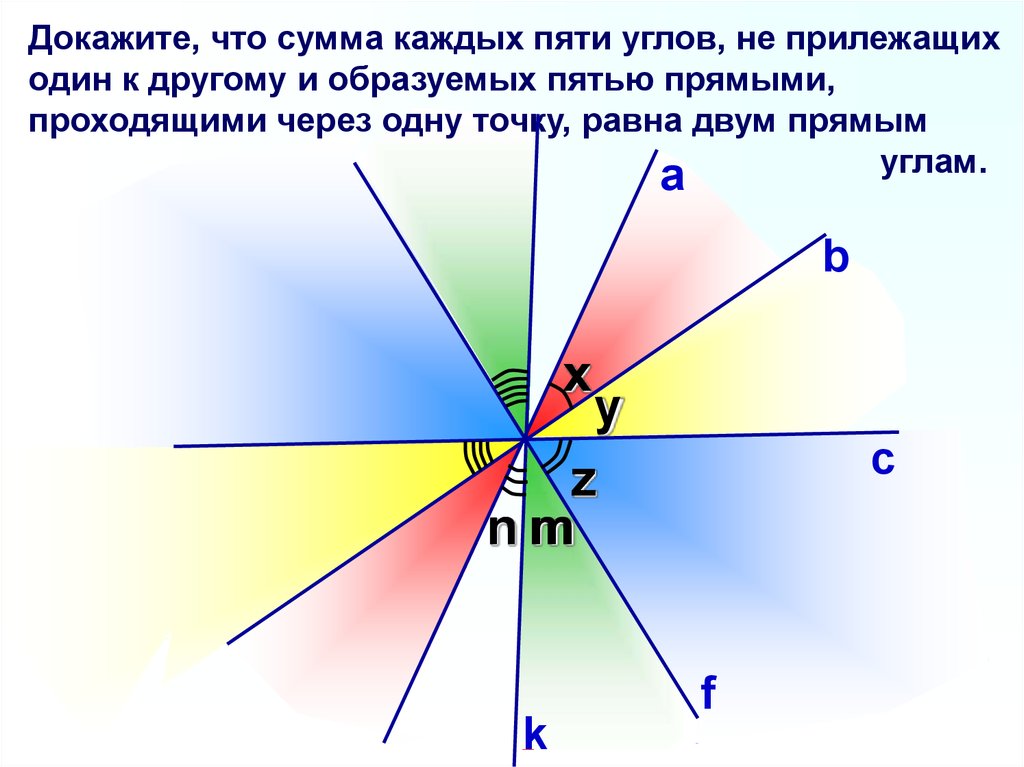
Докажите, что сумма каждых пяти углов, не прилежащих
один к другому и образуемых пятью прямыми,
проходящими через одну точку, равна двум прямым
углам.
а
b
x
х
у
z
nm
k
с
f

4.

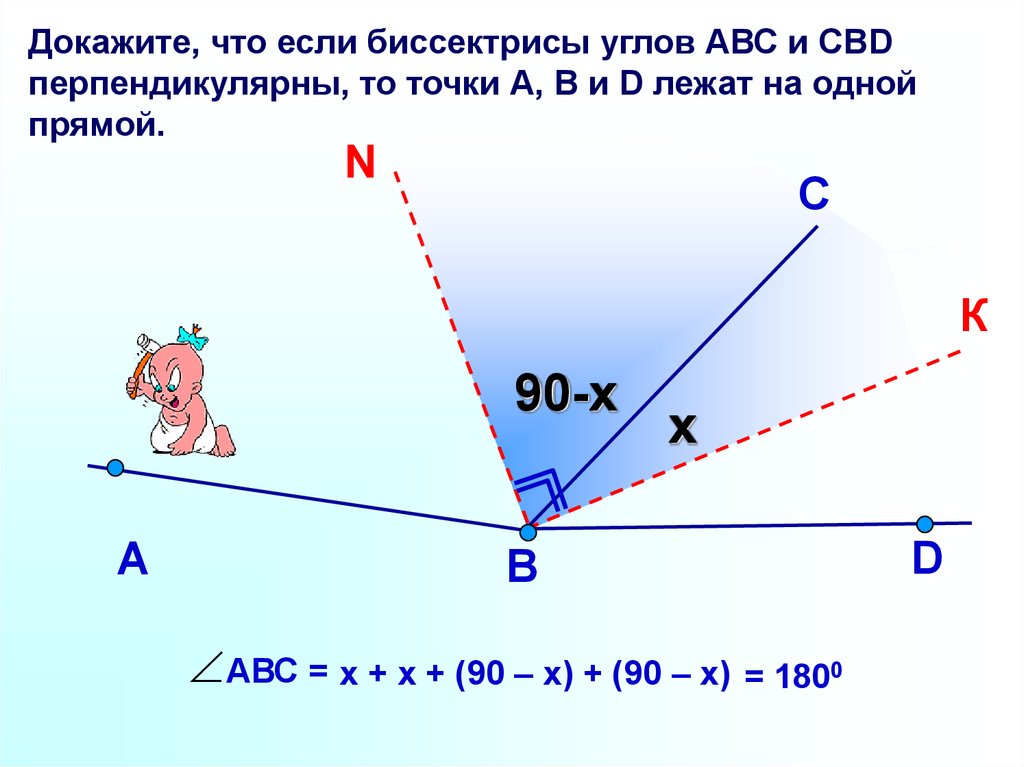
Докажите, что если биссектрисы углов АВС и СВD
перпендикулярны, то точки А, В и D лежат на одной
прямой.
N
С
К
90-х
А
х
В
АВС = х + х + (90 – х) + (90 – х) = 1800
D

5.

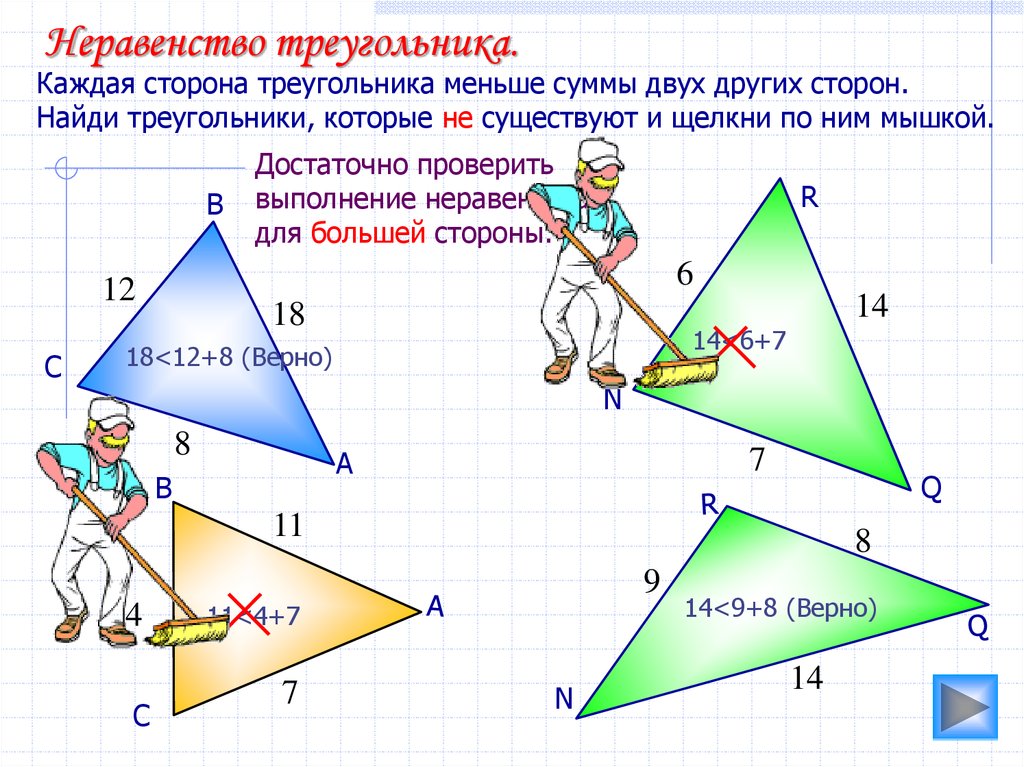
Неравенство треугольника.
Каждая сторона треугольника меньше суммы двух других сторон.
Найди треугольники, которые не существуют и щелкни по ним мышкой.
В
R
6
12
С
Достаточно проверить
выполнение неравенства
для большей стороны.
18
14
14<6+7
18<12+8 (Верно)
N
8
А
В
7
Q
11
4
С
8
9
11<4+7
7
N
14<9+8 (Верно)
14

6.

Найдите х
С
450
х
D
1350
450
6 дм
E
F

7.

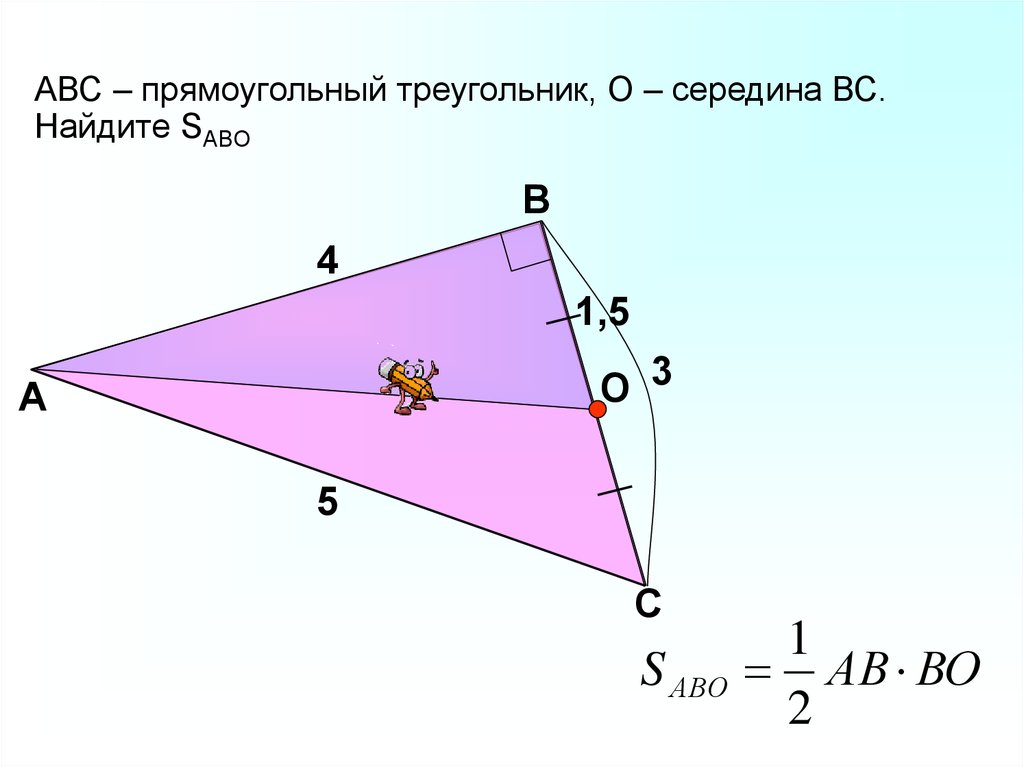
АВС – прямоугольный треугольник, О – середина ВС.
Найдите SABО
В
4
1,5
О 3
А
5
С
S АВО
1
АВ ВО
2

8.

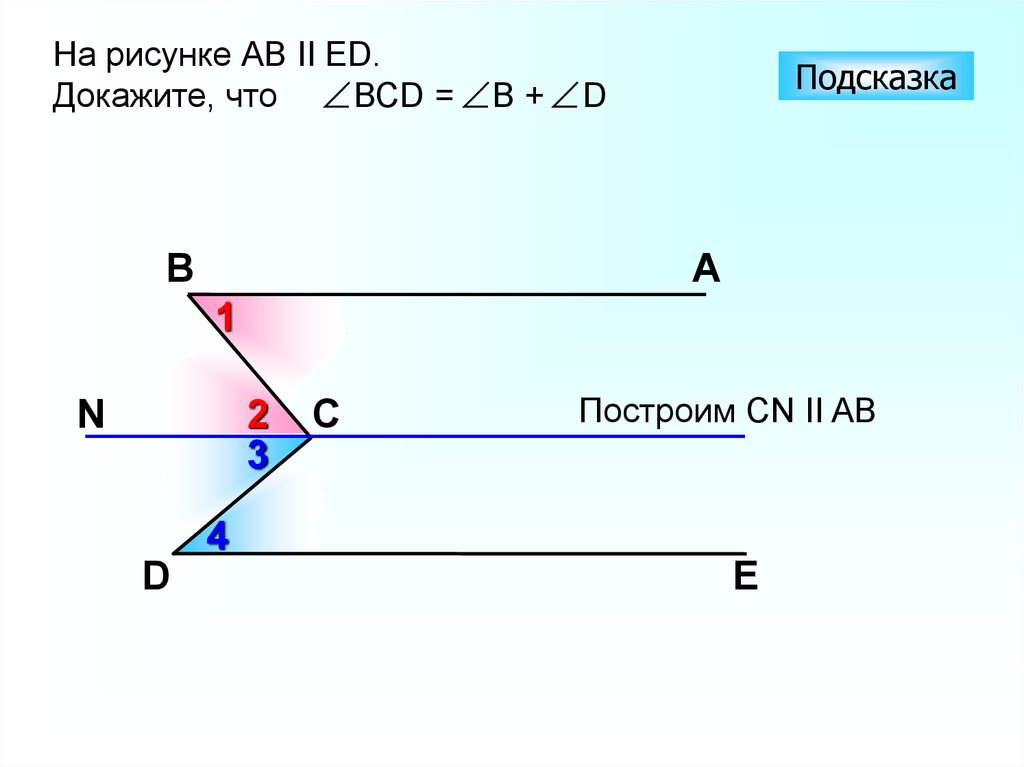
На рисунке АВ II ЕD.
Докажите, что ВСD = B + D
B
Подсказка
A
1
N
2
3
C
Построим CN II AB
4
D
E

9.

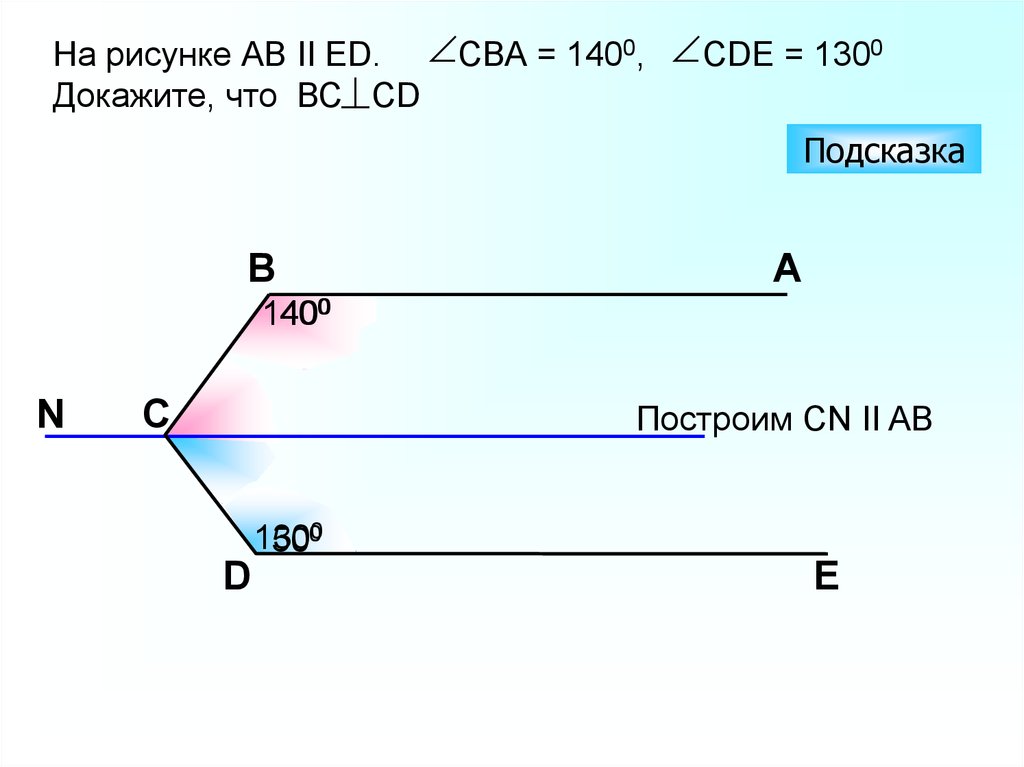
На рисунке АВ II ЕD. CВА = 1400, СDE = 1300
Докажите, что ВС СD
Подсказка
B
A
140
400
N
C
Построим CN II AB
130
50 0
D
E

10.

*
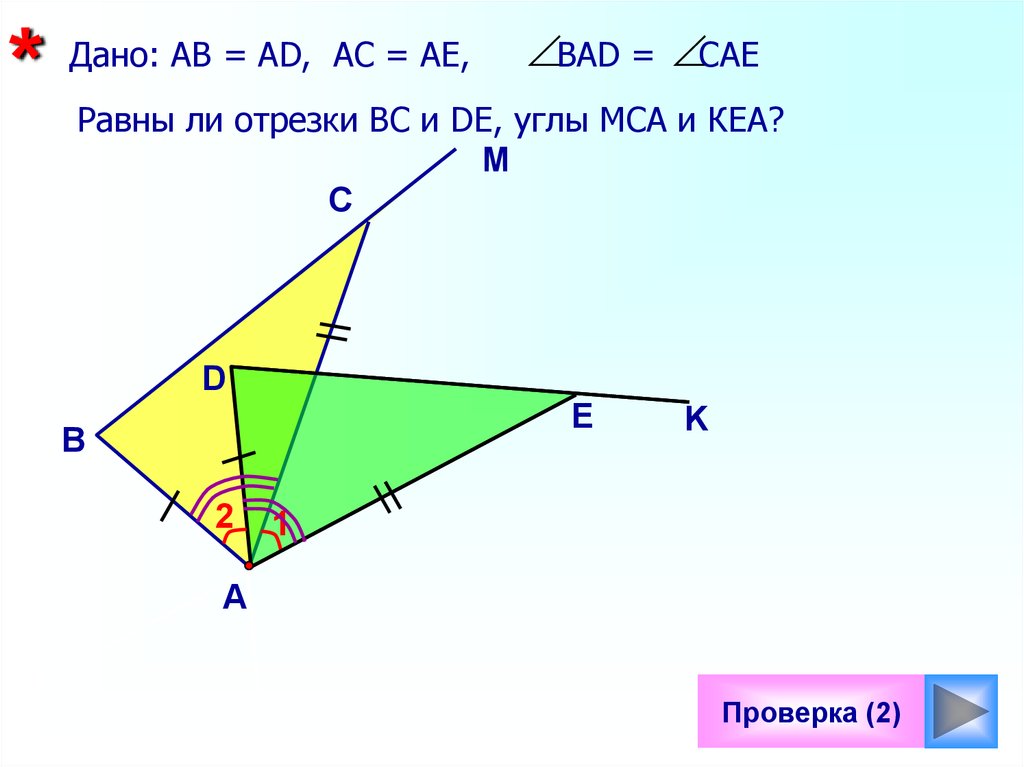
Дано: АВ = АD, АС = АЕ,
ВАD = САЕ
Равны ли отрезки ВС и DE, углы МСА и КЕА?
M
С
D
E
B
2
K
1
А
Проверка (2)

11.

*
Дано: ОА = ОС и
Доказать:
АОВ = ВОС.
АВК = CBК
B
АВО = CBО (по 1 признаку)
34
(I)
1) АВ = ВС; из равенства I
2)
3 = 4; из равенства I
3) ВК – общая сторона.
1 2
О
А
K
АВК = CBК (по 1 признаку)
С
Решение (5)

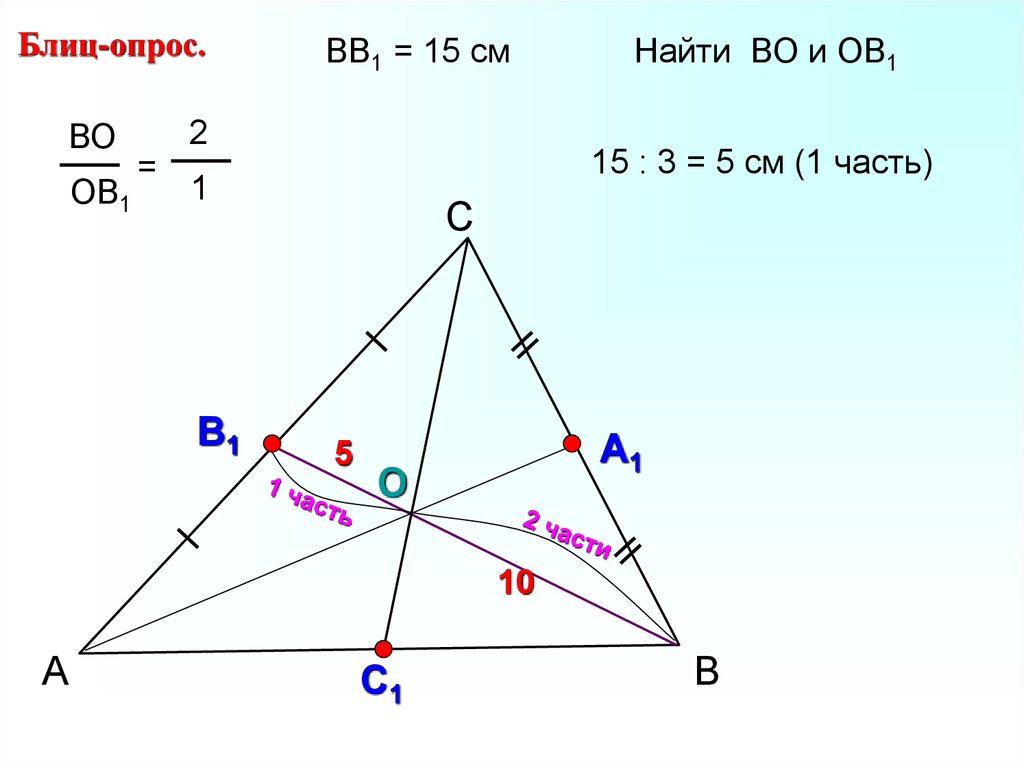
12.

Блиц-опрос.
ВО
ОВ1
ВВ1 = 15 см
2
=
15 : 3 = 5 см (1 часть)
1
В1
Найти ВО и ОВ1
С
5
А1
О
10
А
С1
В

13.

Блиц-опрос.
ВО
ОВ1
ОВ1 = 4 см
Найти ВО и ВВ1
2
=
ОВ1 = 4 см (1 часть)
1
В1
С
4
А1
О
8
А
С1
В

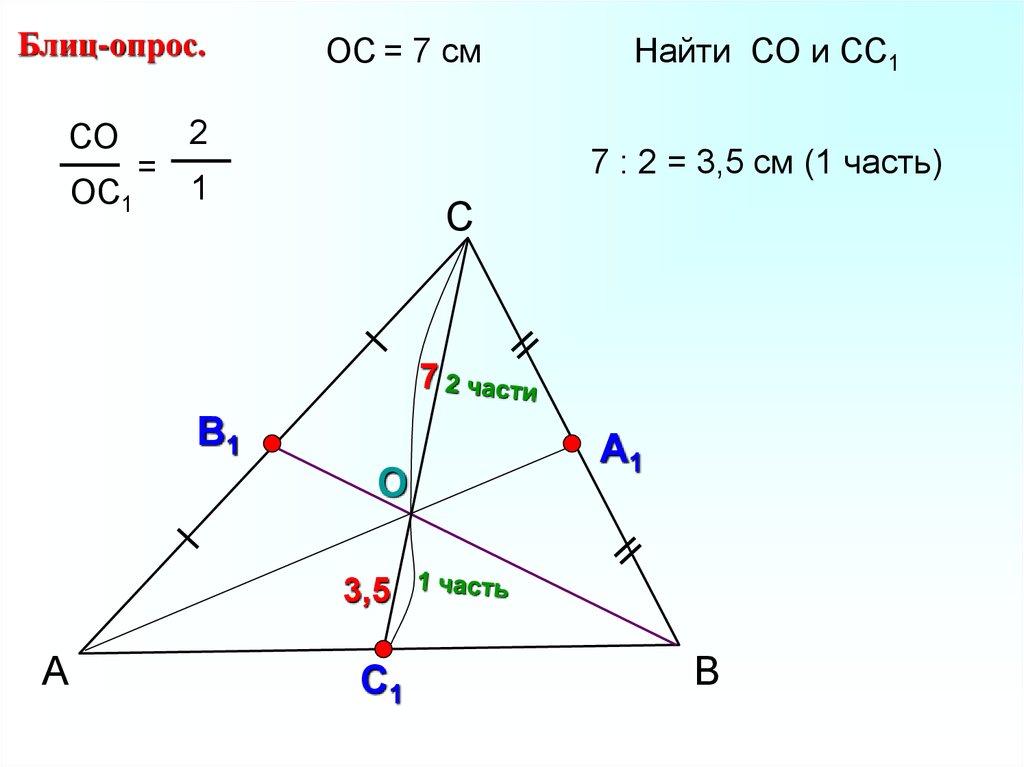
14.

Блиц-опрос.
СО
ОС1
ОС = 7 см
2
=
Найти СО и СС1
7 : 2 = 3,5 см (1 часть)
1
С
7
В1
О
А1
3,5
А
С1
В

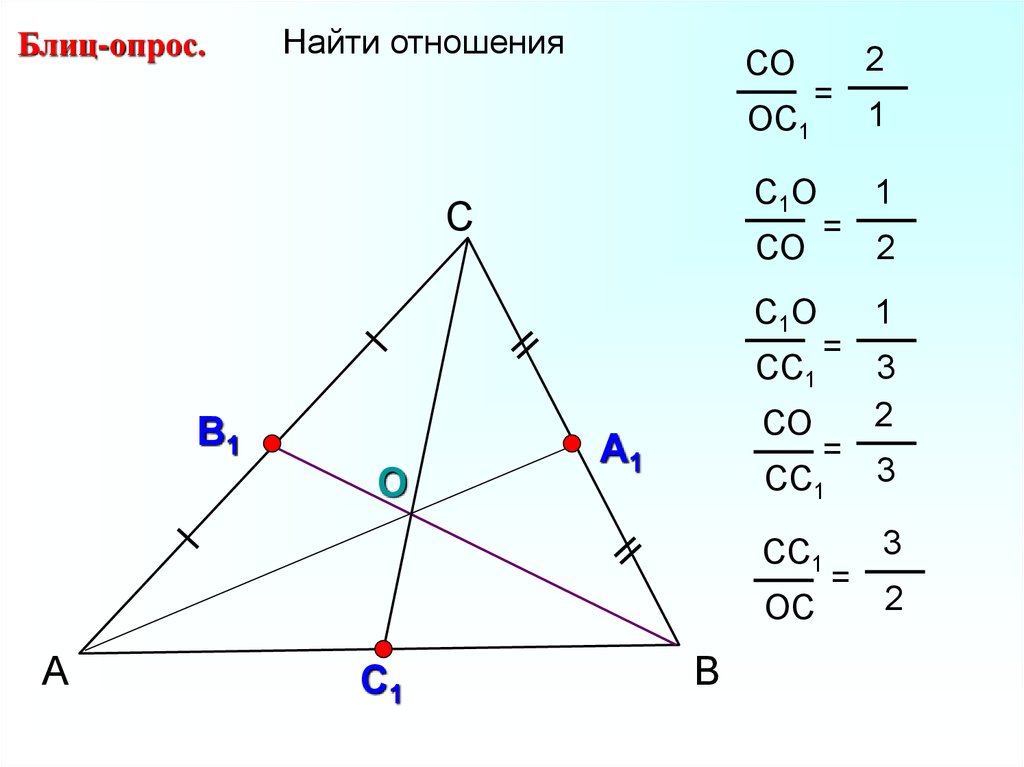
15.

Блиц-опрос.
Найти отношения
СО
ОС1
2
=
С1О
С
СО
С1О
СС1
В1
О
СО
А1
С1
В
1
=
2
1
=
=
3
2
СС1
3
СС1
3
ОС
А
1
=
2

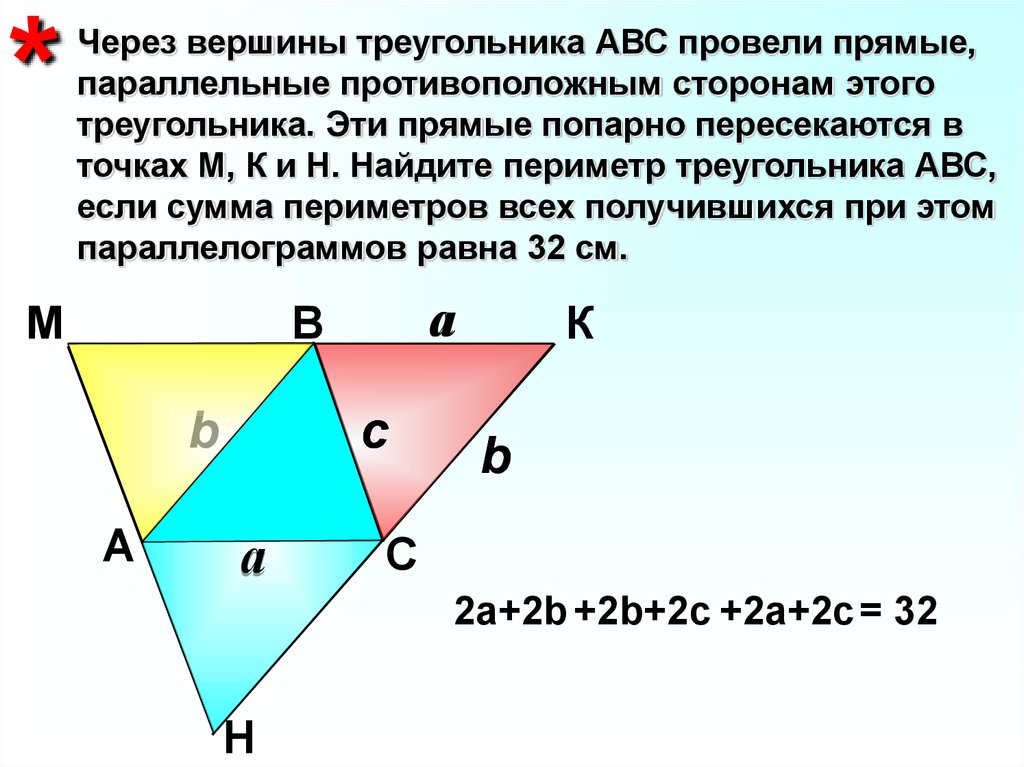
16.

*
Через вершины треугольника АВС провели прямые,
параллельные противоположным сторонам этого
треугольника. Эти прямые попарно пересекаются в
точках М, К и Н. Найдите периметр треугольника АВС,
если сумма периметров всех получившихся при этом
параллелограммов равна 32 см.
М
а
В
b
А
c
а
К
b
С
2a+2b +2b+2c +2a+2c = 32
Н

17.

*
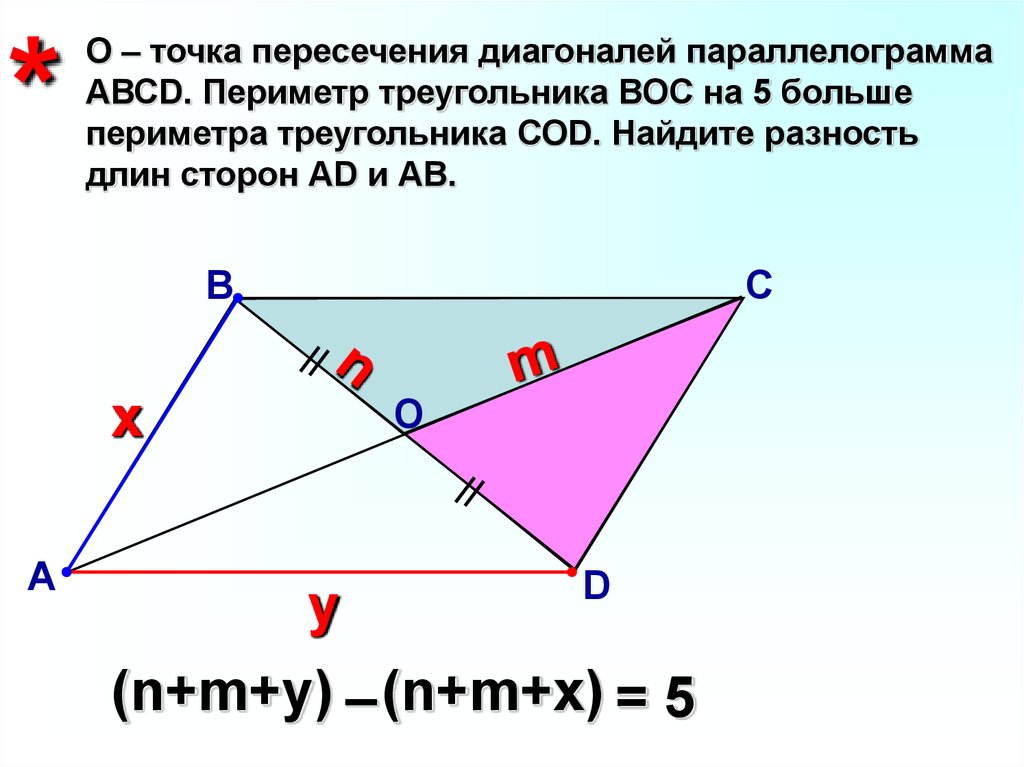
О – точка пересечения диагоналей параллелограмма
АВСD. Периметр треугольника ВОС на 5 больше
периметра треугольника СОD. Найдите разность
длин сторон АD и АВ.
В
С
х
А
О
у
D
(n+m+y) – (n+m+x) = 5

18.

Упражнения по планиметрии на готовых чертежах
Найдите все неизвестные угла квадрата.
В
F
?0
90
1300
С
70
?0
45
?0
?0
45
85
?0
?0 O 9?50
95
?0
85
4?50
?50
4
А
?0 ?
1300 ?
70
Е
D

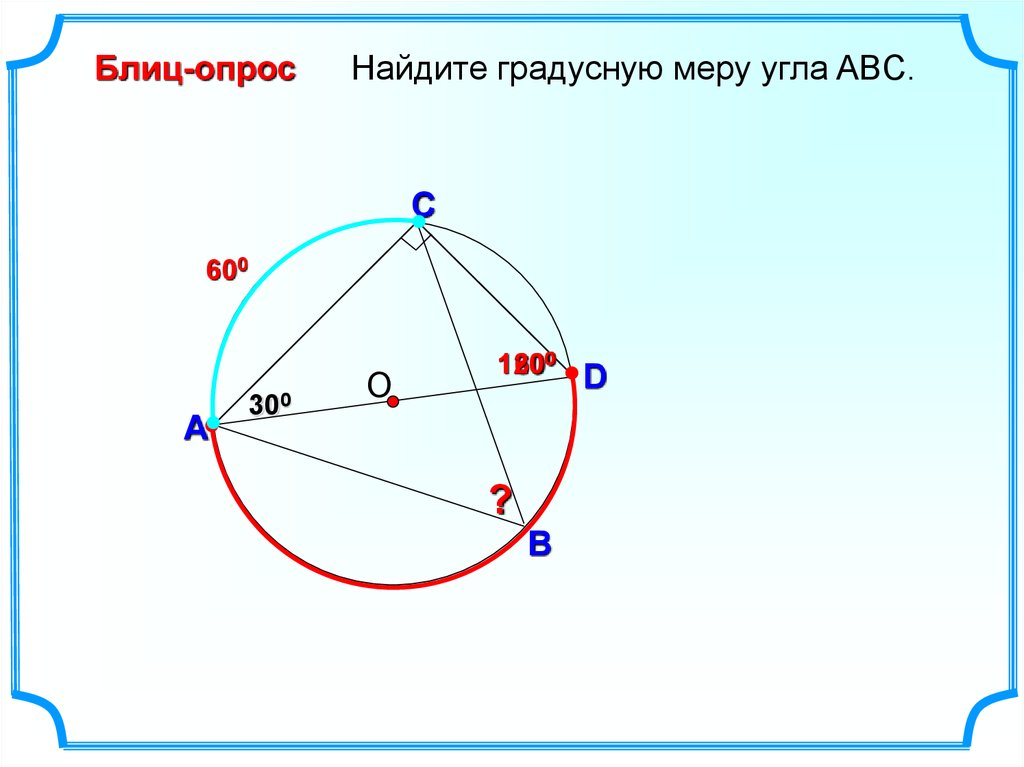
19.

Блиц-опрос
Найдите градусную меру угла ABC.
C
600
A
300
О
120
600 D
?
B

20.

Как нарисовать дуги? Автофигуры, Основные фигуры, Дуга. Зажав клавишу
Shift, рисуем дужку (Дуга 1). Применяя эту клавишу, получаем дугу окружности.
За желтые метки замыкаем окружность (Дуга 2). Копируем. Из копий создаем
новые дуги, концы выделяем точками. Радиус исходной дуги, красной и синей
дуг равны. Поэтому их можно идеально совместить. Для более точного
совмещения зажимаем клавишу Ctrl и используем клавиши перемещения
курсора.
Копия
Дуга 2
Дуга 1
Копия
Дуга 2
Копия

21.

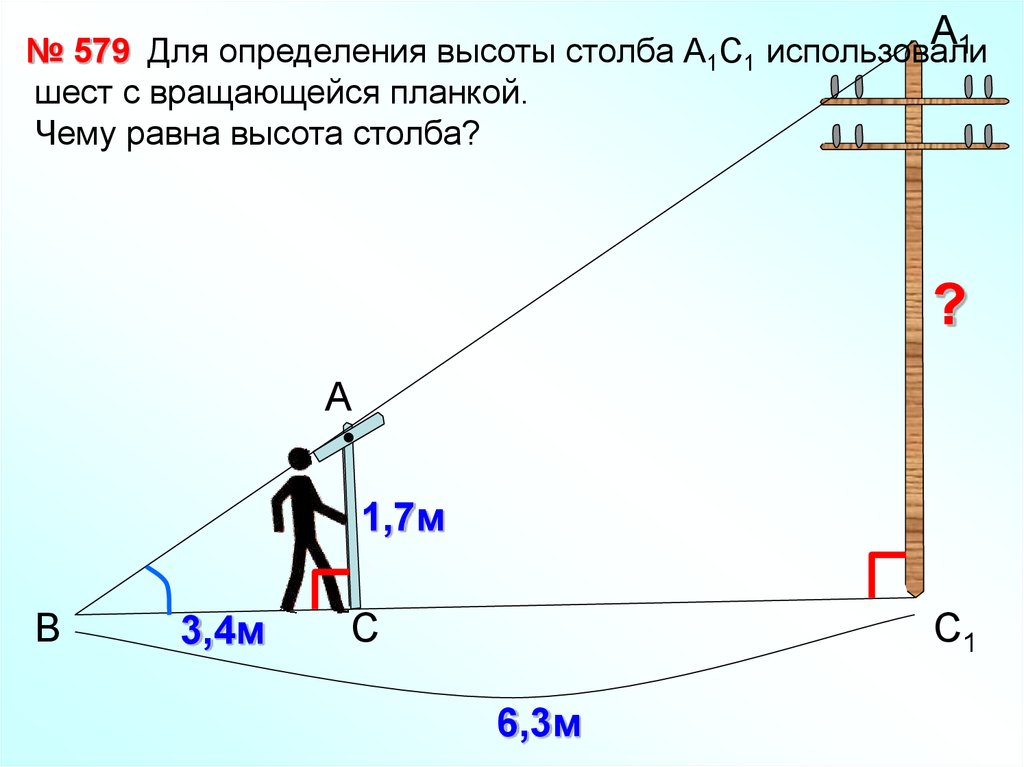
А
1
№ 579 Для определения высоты столба А1С1 использовали
шест с вращающейся планкой.
Чему равна высота столба?
?
А
1,7м
В
3,4м
С
С1
6,3м

22.

№ 582 Для определения расстояния от точки А до
недоступной точки В на местности выбрали точку С и
измерили отрезок АС, углы ВАС и АСВ. Затем построили
на бумаге треугольник А1В1С1, подобный треугольнику
АВС. Найдите АВ, если АС=42м, А1С1=6,3см,
А1В1=7,2см.
В
В1
7,2см
?
А1 6,3см С1
А
42м
С

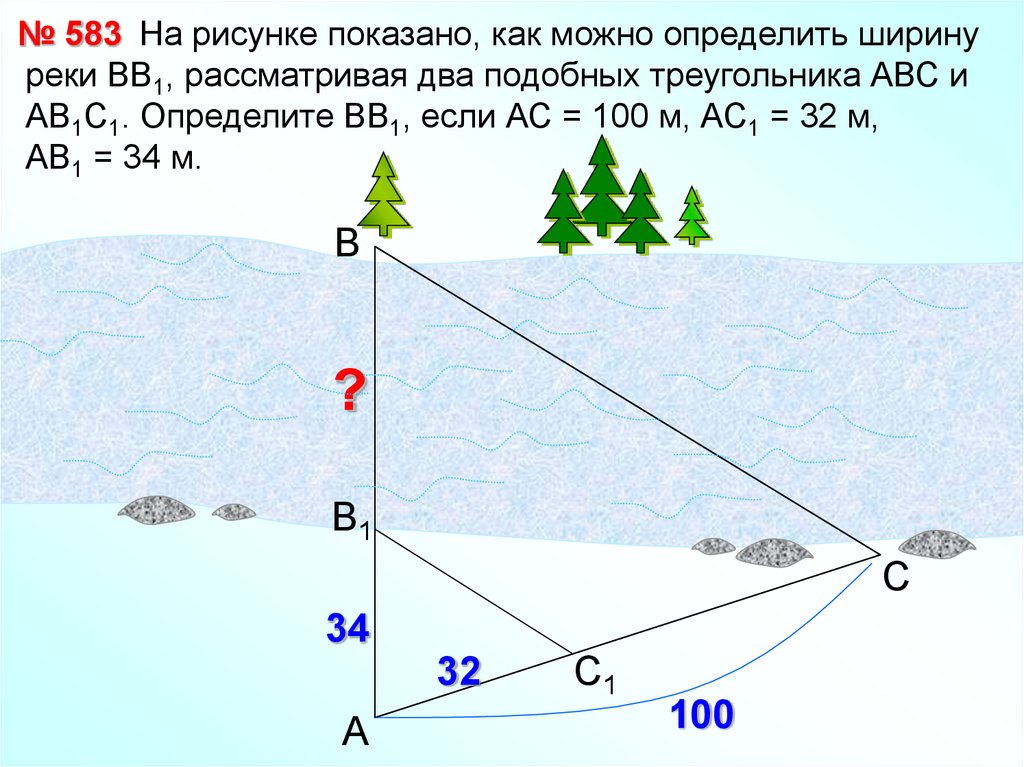
23.

№ 583 На рисунке показано, как можно определить ширину
реки ВВ1, рассматривая два подобных треугольника АВС и
АВ1С1. Определите ВВ1, если АС = 100 м, АС1 = 32 м,
АВ1 = 34 м.
В
?
В1
С
34
32
А
С1
100

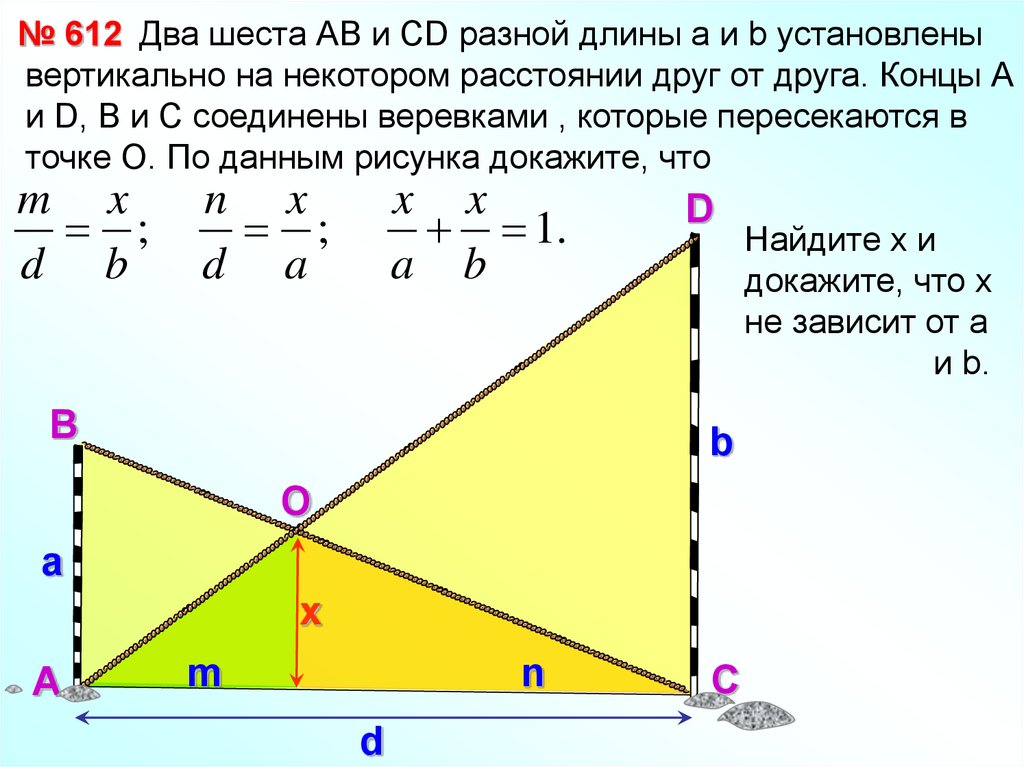
24.

№ 612 Два шеста АВ и СD разной длины а и b установлены
вертикально на некотором расстоянии друг от друга. Концы А
и D, В и С соединены веревками , которые пересекаются в
точке О. По данным рисунка докажите, что
m x
;
d b
n x
;
d a
x x
1.
a b
B
D
b
O
a
x
А
m
n
d
С
Найдите х и
докажите, что х
не зависит от а
и b.

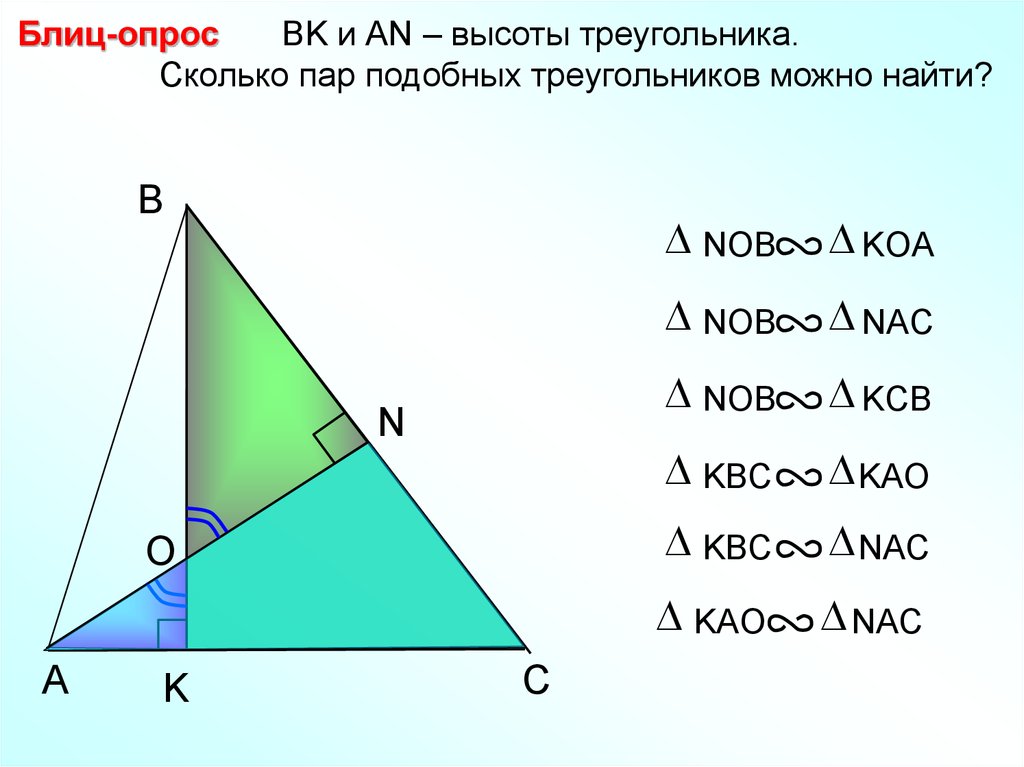
25.

Блиц-опрос
BK и АN – высоты треугольника.
Сколько пар подобных треугольников можно найти?
B
N
О
A
K
C
NOB
KOA
NOB
NAC
NOB
KCB
KBC
KAO
KBC
NAC
KAO
NAC

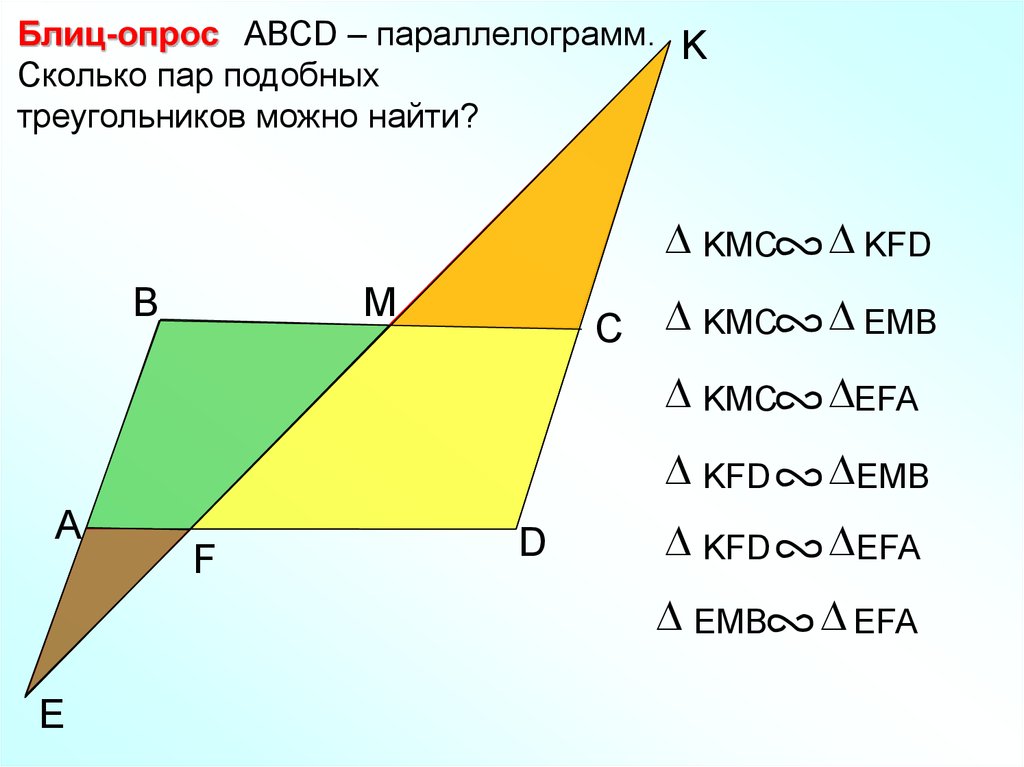
26.

Блиц-опрос АВСD – параллелограмм. K
Сколько пар подобных
треугольников можно найти?
B
А
E
M
F
С
D
KMC
KFD
KMC
EMB
KMC
EFA
KFD
EMB
KFD
EFA
EMB
EFA

27.

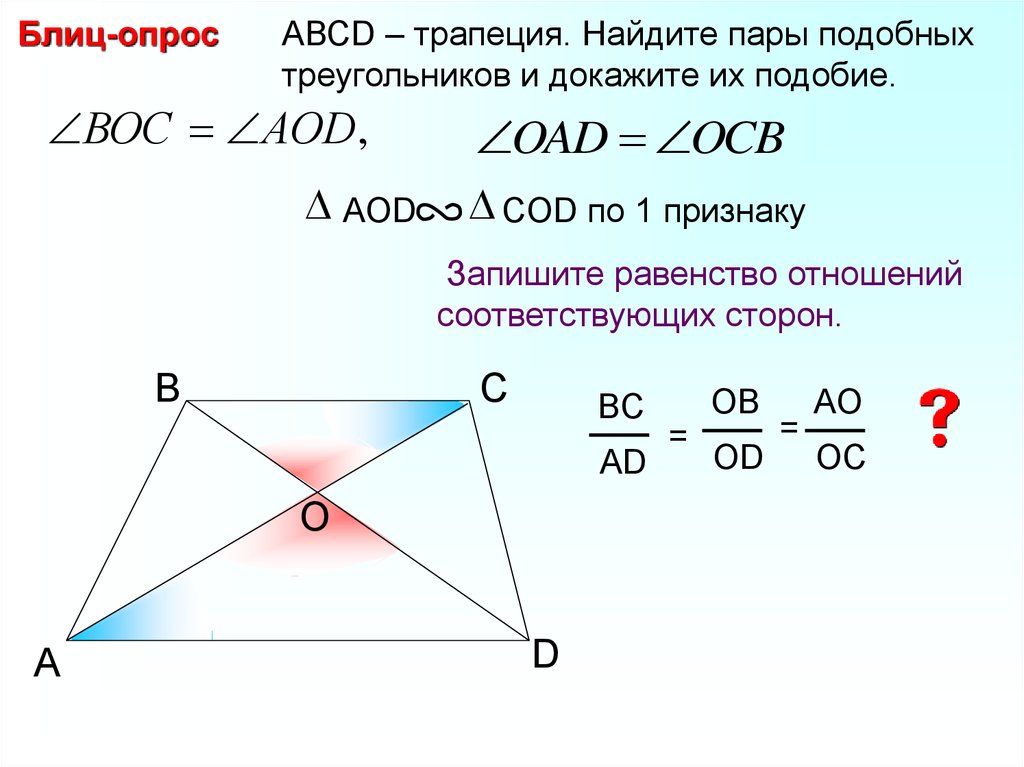
Блиц-опрос
АВСD – трапеция. Найдите пары подобных
треугольников и докажите их подобие.
ВОС АОD ,
AОD
OAD OCB
COD по 1 признаку
Запишите равенство отношений
соответствующих сторон.
С
B
BC
AD
O
A
D
OB
=
OD
=
AO
OC

28.

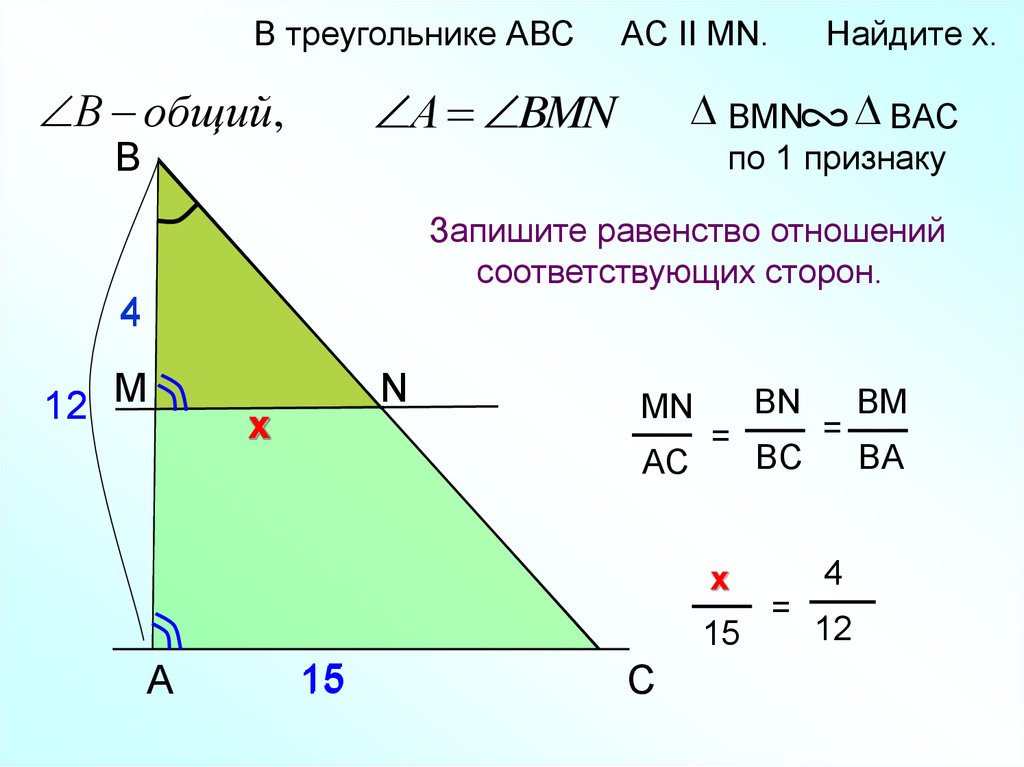
В треугольнике АВС
А BMN
В общий,
Найдите x.
AC II MN.
BMN
BAC
по 1 признаку
B
Запишите равенство отношений
соответствующих сторон.
4
12 М
N
х
MN
AC
BN
=
х
15
A
15
C
BC
=
4
=
12
BM
BA

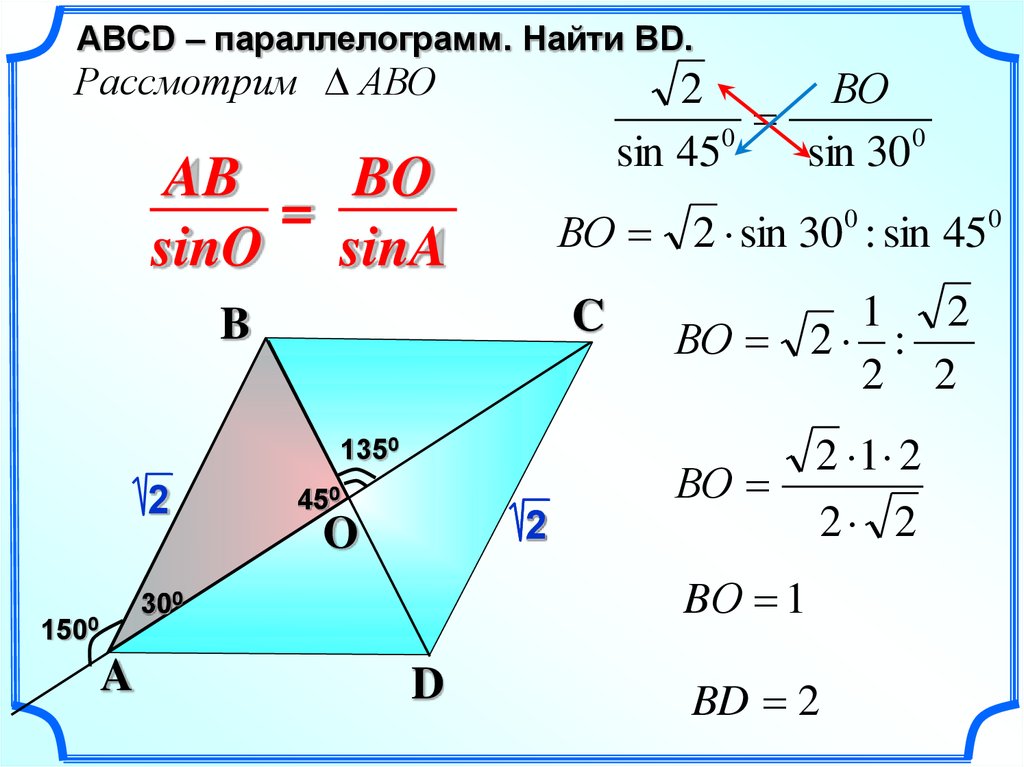
29.

ABСD – параллелограмм. Найти ВD.
Рассмотрим АВО
2
ВО
0
0
sin 45
sin 30
AB
BO
=
sinO sinA
ВО 2 sin 300 : sin 450
C
B
1350
2
ВО
450
2
O
A
2 1 2
2 2
BО 1
300
1500
1 2
ВО 2 :
2 2
D
BD 2

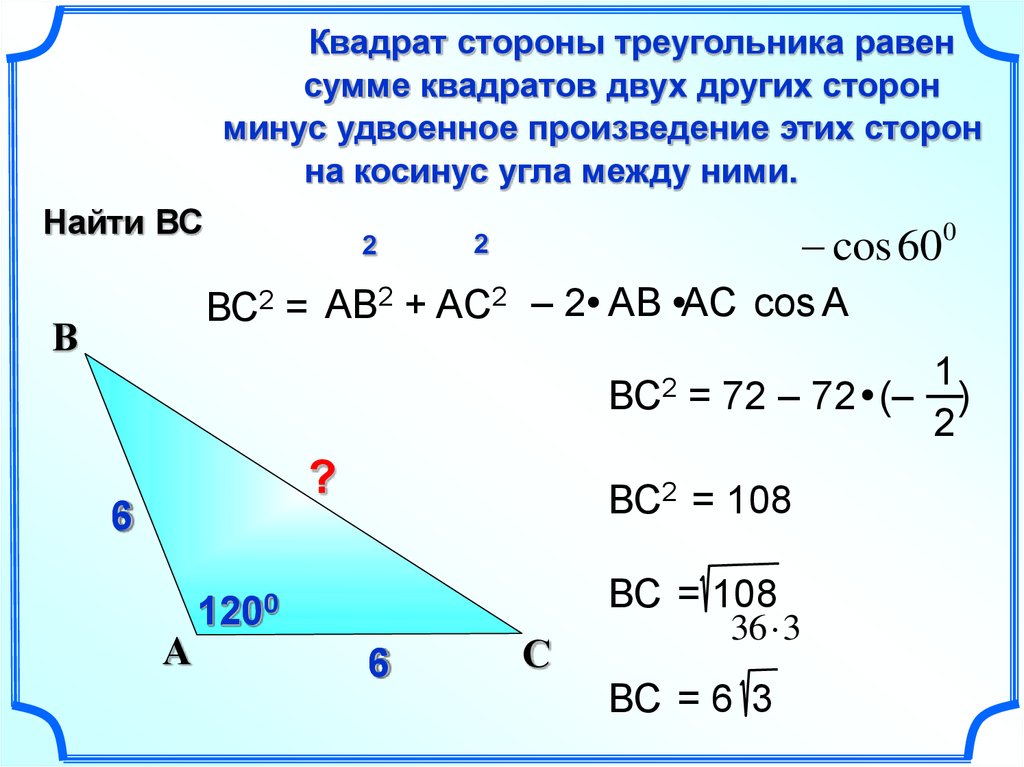
30.

Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
Найти ВС
2
cos 600
2
ВС2 = АВ2 + AC2 – 2 АВ AC cos А
В
ВС2
?
6
А
1
= 72 – 72 (– )
2
ВС2 = 108
ВС = 108
1200
6
С
36 3
ВС = 6 3

31.

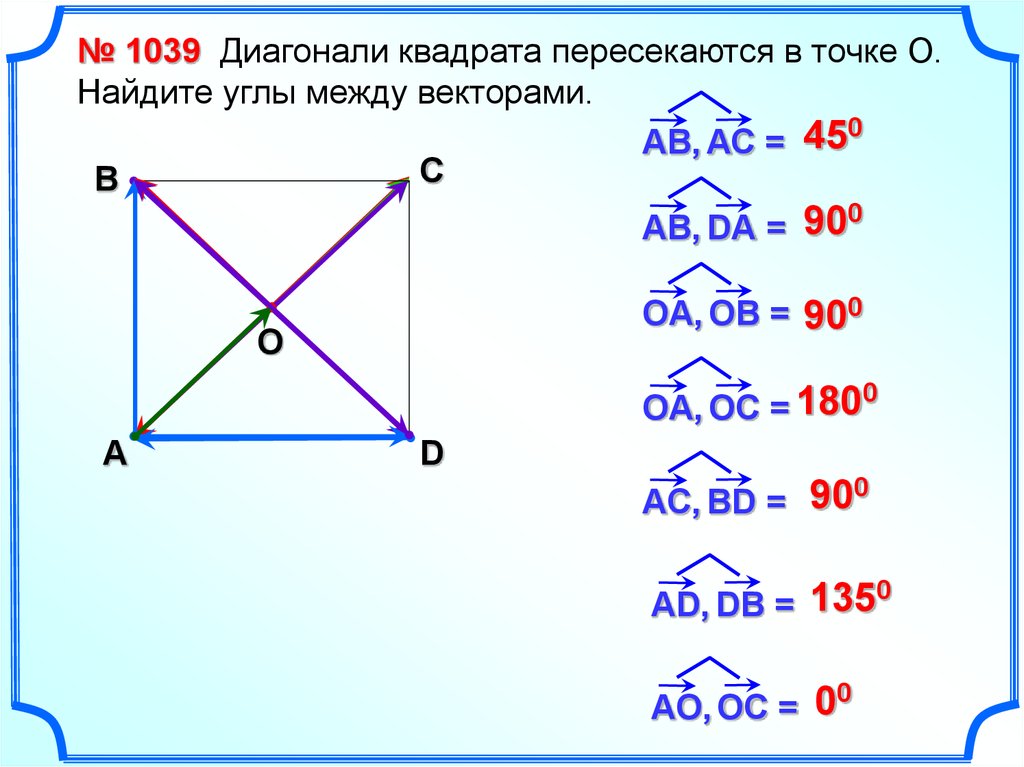
№ 1039 Диагонали квадрата пересекаются в точке О.
Найдите углы между векторами.
0
АВ, АС = 45
С
В
0
АВ, DА = 90
OА, OB = 900
О
OА, OС = 180
А
0
D
0
АC, BD = 90
0
АD, DB = 135
0
АO, OC = 0

32.

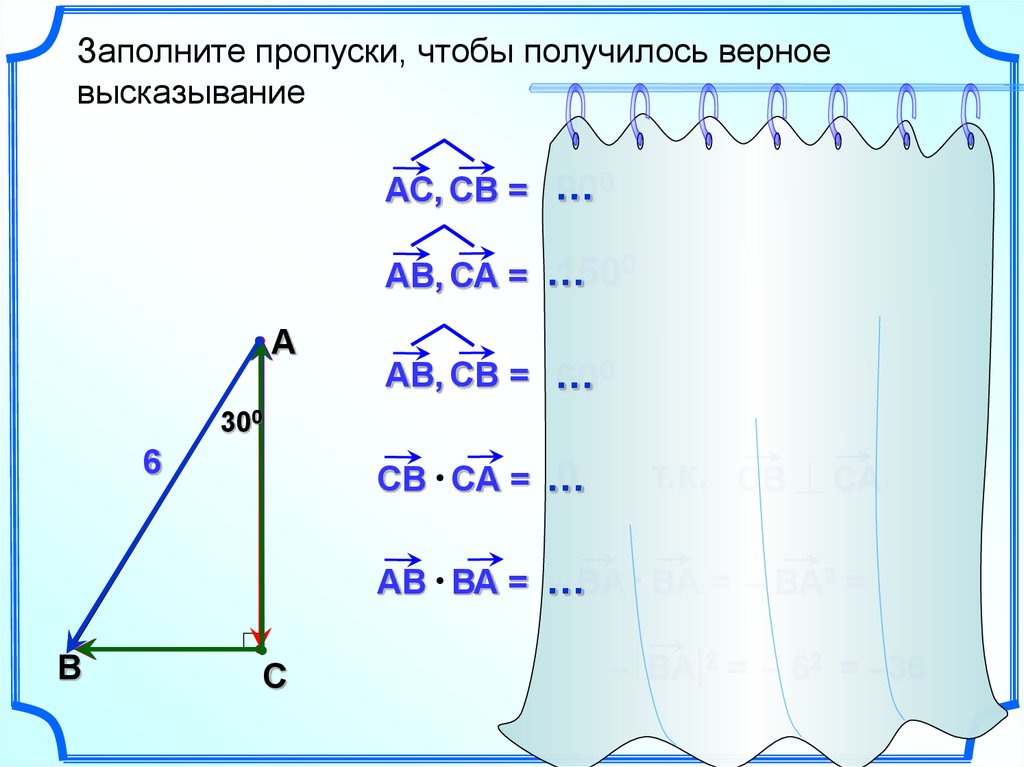
Заполните пропуски, чтобы получилось верное
высказывание
…0
АС, СВ = 90
1500
АВ, СА = …
А
300
АВ, СВ = 60
…0
6
т.к. CВ СА
0
CВ CА = …
АВ ВА = …
– BА BА = – BА2 =
В
С
– BА 2 = – 62 = –36

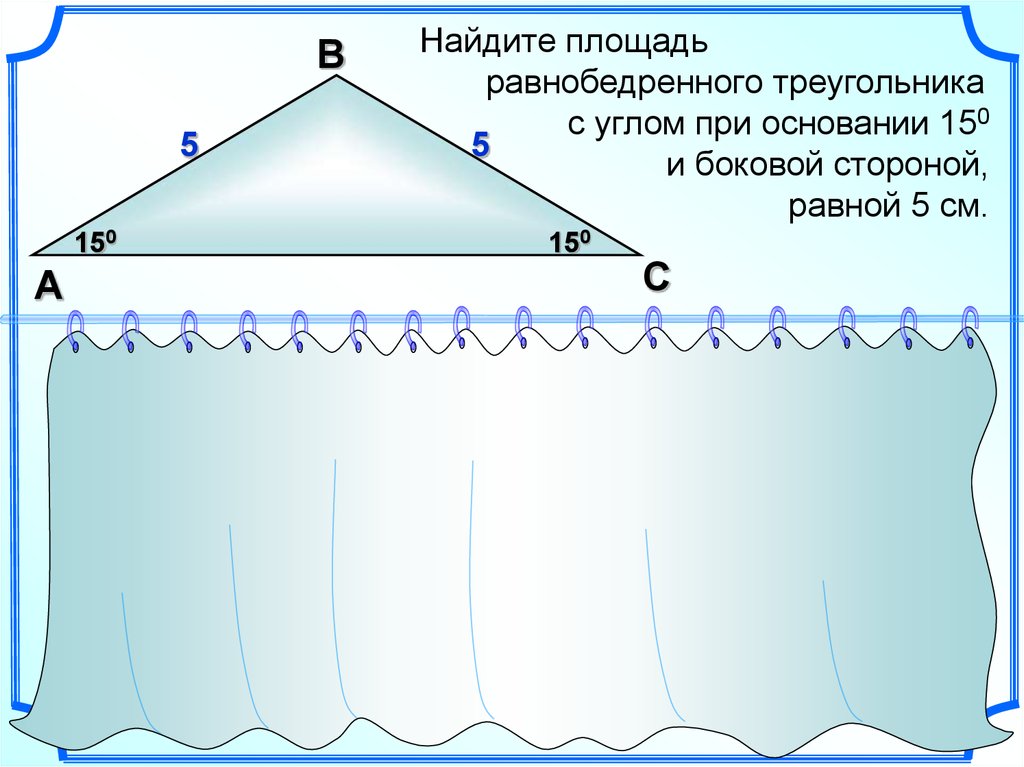
33.

Найдите площадь
равнобедренного треугольника
с углом при основании 150
5
и боковой стороной,
равной 5 см.
В
5
150
150
A
С
1
2
S = ab sina
1
25
25 1 25
S 5 5 sin 150
sin 30
2
2
2 2 4
1 2)
6 (см
4