Лекция №2. Электромагнитное излучение в сплошной среде

1. ОПТИЧЕСКИЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ ЛЕКЦИЯ №2 Электромагнитное излучение в сплошной среде

Астапенко В.А., д.ф.-м.н.
1

2. Микроскопические уравнения Максвелла e, h – напряженности микроскопических электрического и магнитного полей

1 rote
1 h
c t
2 divh 0
3 roth
закон электромагнитной индукции
отсутствие магнитных зарядов
1 e 4
jmicr
c t c
модифицированный закон Ампера
jmicr
- микроскопическая плотность тока
1 e
- плотность тока смещения, введенного Максвеллом
4 t
4 dive 4 ρmicr
закон Кулона в дифференциальной форме
ρ micr
- микроскопическая плотность заряда
2

3. Макроскопическое электрическое поле, магнитная индукция и макроскопическое магнитное в среде усреднение по физически бесконечно малому

Макроскопическое электрическое поле, магнитная
индукция и макроскопическое магнитное в среде
усреднение по физически бесконечно малому объему V
E r
1
e r r dr
V V
B r
1
V
h r r dr
напряженность макроскопического
электрического поля
магнитная индукция
V
H B
напряженность макроскопического
магнитного поля в немагнитном приближении
3

4. Усреднение микроскопических уравнений Максвелла

rot E
rot B
1 B
c t
1 E 4π
jc jb
c t
c
jb
divB 0
div E 4 π ρ b ρ ext
- плотность тока связанных зарядов
j c σ E - плотность тока проводимости
ρ b - плотность связанных зарядов
ρ ext - плотность внешних зарядов
4

5. Поляризация среды (P) P – дипольный момент единицы объема среды

P
jb
t
выражение плотности тока связанных зарядов
через поляризацию вещества в случае,
когда намагниченностью среды можно пренебречь
ρ b div P
jb 4 ρ b c, jb
ρ b
div jb 0
t
выражение плотности связанных зарядов
через поляризацию среды
- четырехмерный вектор плотности тока
закон сохранения заряда, из которого следует,
что в четырехмерном векторе плотности тока
только три компоненты являются независимыми
5

6. Электрическая индукция и диэлектрическая проницаемость среды

D E 4 π P - индукция электрического поля
В линейном приближении:
Di r, t εˆ E r, t dτ ε ij r , τ E j r r , t τ dr
0
e
Ei r, t 4 π dτ ij r , τ E j r r , t τ dr
0
В фурье-представлении:
Di k , ω εij k ,ω E j k ,ω ij 4 χ ij e k ,ω E j k,ω
Pi k ,ω χ ij k ,ω E j k,ω
e
ij k,ω ij 4 ij e k,ω
ij, ij(e) - тензоры диэлектрической проницаемость и восприимчивость
6

7. Диэлектрическая проницаемость изотропной среды

ki k j
ij k , 2 k , ij 2
k
k
ki k j
l
D k , k , E k ,
l
l
l
D k , , E k , k
l
l
t
k,
D k , k , E k ,
t
t
t
D k , , E k , k
t
t
В пренебрежении пространственной дисперсией:
l k 0, t k 0,
ij ij тензор диэлектрической проницаемости
изотропной среды превращается в скаляр
7

8. Формулы Крамерса-Кронига

1
e
e
e V .P.
dω
ω ω
1
e V .P.
dω
ω ω
f x
a f x
f x
V .P.
dx lim
dx
dx
0 x a
x a
a x a
- интеграл в смысле
главного значения
Пользуясь приведенными равенствами, можно по мнимой части диэлектрической
восприимчивости восстановить действительную часть и наоборот.
8

9. Общие соотношения для функций отклика вещества  и 

Общие соотношения для функций отклика
вещества и
χ ω χ ω
χ ω χ ω
χ ω χ ω
ε 1 4π
j
N jβ
ε 2 3 j
β
j
ω , N j
формула Клаузиуса-Мосотти
динамическая поляризуемость и концентрация атомов среды
ε ω 1
ω2p
ω2
4 e2 N e
ωp
me
«плазменная» формула для диэлектрической
проницаемости
- плазменная частота
9

10. Поляризуемость атомов вещества

ε ω 1 4 π N j β j ω - для разреженных сред, когда 1
j
E E a
me2 e 5
4
5.14 10 B см
9
E a2 me4 e10 c
16 Вт
I I a c
3
.
52
10
8π
8 π 8
см 2
d t 2 Re β ω E ω exp i ω t
f 0n
e2
β ω
me n ω 02n ω 2 i ω γ 0n
f jn
2 me ω jn n d j
2
3e g j
d ω β ω E ω
общее выражение для поляризуемости
2
-сила осциллятора атомного перехода
(безразмерная величина)
10

11. Формула Клаузиуса-Мосотти

P
1
E
4
P N Eloc
Eloc E ELor
E Lor
4
P
3
ELor поле Лоренца
ε 1 4π
Nβ
ε 2 3
Здесь при вычислении локального поля
производится усреднение поля по атомам
«минус» выделенный атом
n2 1 4π
N β формула Лоренц-Лорентца
2
n 2 3
n – показатель преломления вещества
11

12. Макроскопические уравнения Максвелла в немагнитном приближении (B=H)

С учетом выражения для плотности тока связанных зарядов
и определения электрической индукции получаем:
1 H
rot E
c t
1 D 4π
rot H
E
c t
c
div H 0
divD 4πρext
Материальное соотношение
D D E ˆ E
12

13. Учет намагниченности вещества

jb
P
c rotM
t
учет намагниченности среды M в выражении
для плотности тока связанных зарядов
Добавление ротора в выражении для плотности тока не меняет уравнения
сохранения заряда, в котором фигурирует дивергенция плотности тока
ρ b
div jb 0
t
Определение напряженности макроскопического магнитного поля в среде:
H B 4π Μ
«Следует помнить, что в действительности истинное среднее значение
напряженности <магнитного поля> есть B, а не H» Л.Л. т.8
13

14. Магнитная проницаемость и восприимчивость вещества

B H для изотропной среды; Bi ij H j общий случай
lim B H H 0 начальная магнитная проницаемость
d B H дифференциальная магнитная проницаемость
1 4 m
(m) – магнитная восприимчивость вещества
(m) >0 – парамагнитная среда ( (m) <<1)
(m) <0 – диамагнитная среда ( (m) <<1)
>>1 – ферромагнетики, <0 – метаматериал
14

15. Численные значения магнитной проницаемости

15

16. Макроскопические уравнения Максвелла в общем случае

Используя выражения для плотности тока связанных зарядов через
поляризуемость и намагниченность среды и определение напряженности
магнитного поля в веществе, приходим к следующим макроскопическим
уравнениям Максвелла в общем случае:
1 B
rot E
c t
1 D 4π
rot H
E
c t
c
divB 0
divD 4πρext
Материальные соотношения
D D E ˆ E
B B H ˆ H
16

17. Разложение электромагнитного поля по плоским волнам

E r, t E k , ω exp i k r ω t
H r, t H k , ω exp i k r ω t
переход к плоским волнами в уравнениях в частных производных
превращает дифференциальные операторы в алгебраические:
i
t
div i k
rot ik
17

18. Уравнения Максвелла в среде в фурье-представлении

Подставляя формулы из предыдущего слайда в уравнения Максвелла,
получаем систему алгебраических уравнений:
ω
k E k , ω H k , ω
c
k H k,ω 0
ω
4π σ
k H k , ω ε i
E k ,ω
c
ω
ε k E k,ω 0
18

19. Диэлектрики и проводники

Предел диэлектрической среды (ток проводимости пренебрежимо мал):
ω
k H k , ω ε k , ω E k , ω
c
ωε k,ω 4π σ
Случай проводника (ток смещения пренебрежимо мал):
4π σ
k H k , ω i
E k , ω
с
ωε k,ω <<4π σ
Таким образом, одно и то же вещество на разных частотах может вести себя
и как проводник и как диэлектрик
ε k, ω ε k, ω i
4π σ
ω
обобщенная диэлектрическая проницаемость:
первое слагаемое в правой части содержит отклик
связанных зарядов на электрическое поле, второе
слагаемое описывает отклик свободных зарядов
19

20. Поперечная электромагнитная волна в диэлектрике

Исключая из 1-го и 3-го уравнений Максвелла магнитное поле, находим:
ω2
k E k , ω k k E k , ω 2 ε ω E k , ω
c
2
a b c b a c c a b
E k , k поперечная ЭМ волна: k E k ,ω 0
t
Волновое уравнение в фурье-представлении для поперечной ЭМ волны
2 ω2
t
ω2
2
k 2 ε E k ,ω 0 k 2 ε ω
c
c
закон дисперсии для поперечной волны
05.01.2017
20

21. Комплексный показатель преломления (в немагнитном приближении =1)

Комплексный показатель преломления
(в немагнитном приближении =1)
ω2
ω2
ω
ω
k 2 ε ω 2 ε ω i ε ω ; k n ω s n ω i κ ω s;
c
c
с
с
2
n2 κ 2 ε ; 2 n κ ε
n
1
1
ε ε 2 ε 2 ; κ
2
2
комплексный показатель
преломления вещества
ε 2 ε 2 ε
1 ε 2
ε
1) ε ε ; ε 0 n ε 1 ε ; κ
8 ε
2 ε
2) ε <<ε ; ε <0 n 0; κ
s 1
ε : ε ω 1
ω2p
ω
2
0.
для ω<ω p

22. Дисперсия поперечных электромагнитных волн в общем случае

ω2
ω2
k 2 ε ω 2 ε ω i ε ω ω i ω
c
c
2
k k i k
k n ω
k // k
ω
ω
s n ω i κ ω s
с
с
s 1, s единичный вектор в направлении распространения волны
Комплексный показатель преломления вещества:
n ω n ω i κ ω
05.01.2017
22

23. Комплексный показатель преломления (в общем случае)

n2 κ 2 ε
система уравнений для определения
действительной и мнимой части КПП
2 n κ ε +
n
1
ε
2
κ
1
2
05.01.2017
ε ε +
2
ε ε +
2
2
2
ε
решение системы
в общем случае
(с учетом магнитных
свойств среды)
23

24. Распространение электромагнитной волны в веществе

Из 1-го уравнения Максвелла следует соотношение между амплитудами и фазами
напряженности электрического поля и магнитной индукцией в среде:
κ
B k , ω n2 κ 2 exp i arctg s E k , ω
n
ωn
c
ω
E r, t E k , ω exp i
z
t
κ
z
n
c
c
v ph
c
n
Фазовая скорость
ω
I z I 0 exp 2 κ z
c
α ext 2 κ
05.01.2017
ω
коэффициент экстинкции (ослабления) излучения
c
24

25. Немагнитная среда (=1)

Немагнитная среда ( =1)
ω
ε ω
I z I 0 exp 2 κ z ε >0, ε ε I 0 exp
z
c
c
ε
Изменение интенсивности излучения с расстоянием определяется
знаком мнимой части диэлектрической проницаемости:
>0 – ослабление излучения; <0 – усиление излучения
ω
ω
I z I 0 exp 2 κ z ε <0, ε 0 I 0 exp ε
z
c
c
Этот случай реализуется, например, в металлах на частотах меньших плазменной
05.01.2017
25

26. Диэлектрическая проницаемость металла

2
p
DS 1
формула Друде-Зоммерфельда
i
c2
int er 1 2
вклад межзонных переходов
2
0 i
для золота:
c 2.96 эВ
05.01.2017
0 2.76 эВ
0.59 эВ
26

27. Комплексный коэффициент преломления в металле [Johnson P.B., Chirsty R.W. 1972]

8
8
nAg( ) 6
nAu( ) 6
Ag( )
4
Au( )
4
2
0
2
1
2
3
4
5
6
0
1
2
3
4
5
6
Экспериментальные зависимости действительной (сплошная кривая) и мнимой
(пунктир) частей показателя преломления серебряной пленки (левый график) и
золотой пленки (правый график) в зависимости от энергии фотона;
по оси ординат отложена энергия фотона в электрон-вольтах
05.01.2017
27

28. Усиление излучения в среде

1 D
B
divS
E
H
4 π t
t
F t
F0 e
i ωt
F0
e
i ωt
S
q ω
2
c
E H
4π
ω
2
2
ε ω E0 ω H 0
8π
ω ωnm nm
χ res ω gm β m
e
res
N
N
ω m n
gm gn
χ
e
res
ω
N
N
π e2
g m f nm Gmn ω m n
2 me
gm gn
Nn Nm
при n m условие усиления излучения
gn
gm
Nn gn Nm gm инверсия населенности
05.01.2017
28

29. Волновой пакет и групповая скорость

F z , t Re F k exp i k z ω k t dk
квазимонохроматическое излучение : ωc ω 2 ω ωc ω 2, ω ωc
ω k ωc
F z, t
2 sin ξ k , z, t
F0
cos kc z ωc t , ξ k , z, t k 2 z u t
π
ξ k , z, t
F k z, t
u
05.01.2017
ω kc
k k c , ωc ω k c
k
2 sin ξ k , z, t
F0
огибающая волнового пакета
π
ξ k , z, t
ω kc
групповая скорость
k
29

30. Корпускулярно-волновой дуализм

Для фотона:
u
ω
ε
u
k
p
ε ω
p k
Для нерелятивистской частицы
ε p p2 2 m u p m v
Для релятивистской частицы
ε p m2 c 4 p 2 c 2 u
05.01.2017
ε
p c2 v
p
30

31. Фазовая и групповая скорость в плазме

ε ω 1
ω2p
ω2
ω2 ω2p
ω
k ω ε ω
c
c
1
u
dk ω dω
c
u
ω2 ω2p c ε ω
ω
v ph
c
c
n ω
ε ω
v ph u c2
v ph c
05.01.2017
u c
31

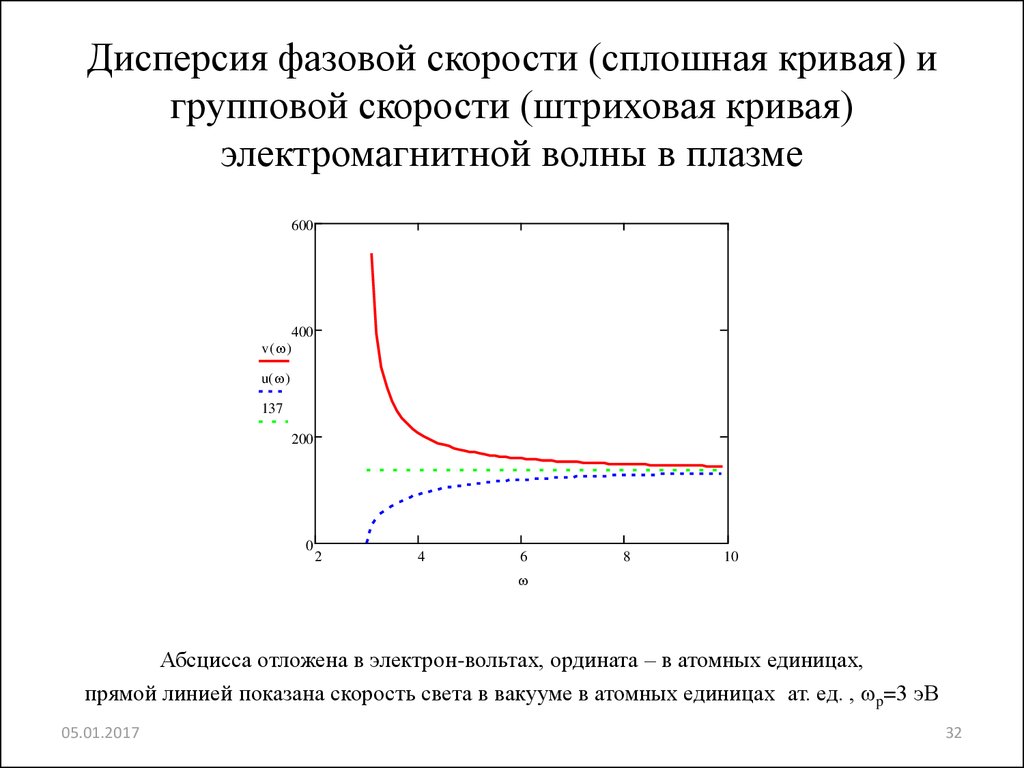
32. Дисперсия фазовой скорости (сплошная кривая) и групповой скорости (штриховая кривая) электромагнитной волны в плазме

600
v( )
400
u( )
137
200
0
2
4
6
8
10
Абсцисса отложена в электрон-вольтах, ордината – в атомных единицах,
прямой линией показана скорость света в вакууме в атомных единицах ат. ед. , p=3 эВ
05.01.2017
32