Сходимость последовательности СВ

1. Сходимость последовательности СВ

Сходимость по вероятности
Последовательность СВ X1, X 2 ,..., X n ,...
сходится к Х по вероятности
Р
P
X n X lim Р X n X 1
n
n
0
Пример X n ~ Ber pn , pn
n
lim Р X n 0
n
Xn
0
1
P
1- pn
pn
lim Р 0 0 lim 1 pn 1
n
n
Р
X n 10
n

2. Сходимость последовательности СВ

Сходимость по распределению d
Последовательность СВ
X1, X 2 ,..., X n ,...
сходится к Х по распределению
X n X lim Fn x F x
n
d
n
в точках непрерывности F(x)
Пример
X n ~ Bin n; p , p 1
X lim X n ~ P a
n
P
d
2

3.

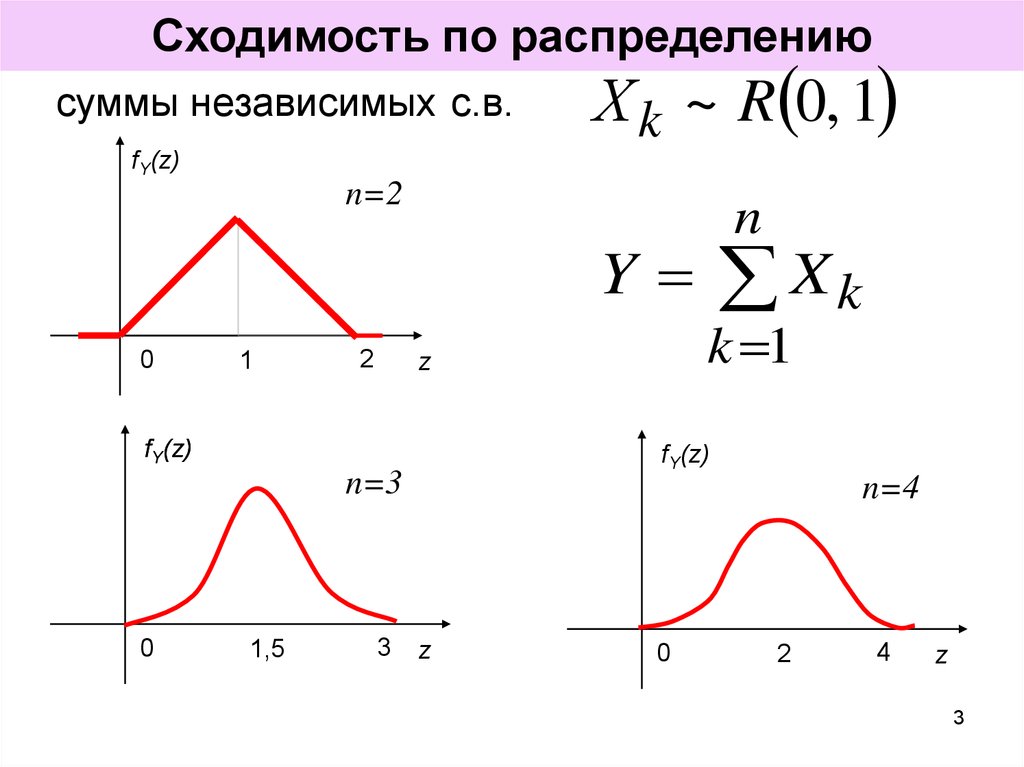
Сходимость по распределению
суммы независимых с.в.
Х k ~ R 0, 1
fY(z)
n=2
n
Y
0
1
2
fY(z)
n=3
0
1,5
k 1
z
fY(z)
3
Xk
n=4
z
0
2
4
z
3

4.

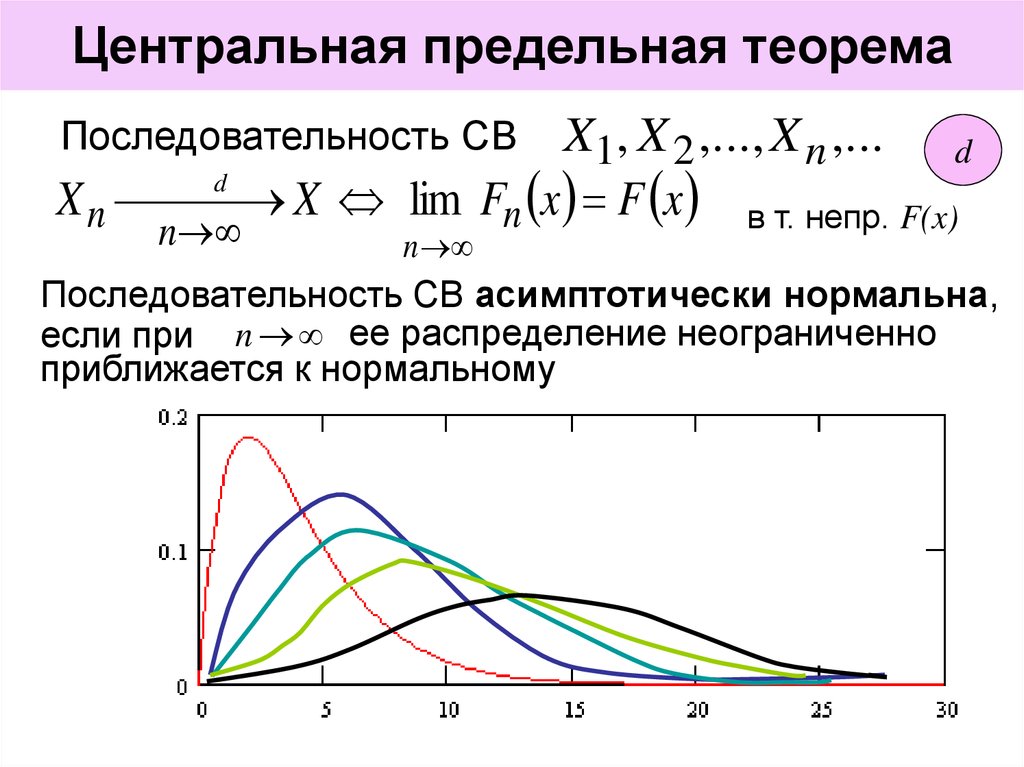
Центральная предельная теорема
Последовательность СВ
X1, X 2 ,..., X n ,... d
d
X n X lim Fn x F x в т. непр. F(x)
n
n
Последовательность СВ асимптотически нормальна,
если при n ее распределение неограниченно
приближается к нормальному
4

5.

Центральная предельная теорема
Пусть СВ X 1 , X 2 ,..., X k ,...независимы, одинаково
распределены с м.о. m и с.к.о.
Тогда СВ
M Yn
n
Yn
n
Xk
k 1
M X k n m
k 1
асимптотически нормальна
D Yn
n
D X k n
k 1
Yn nm
N 0, 1
n
n
d
5
2

6.

Пример При составлении статистического отчета
складывают 300 чисел, округляя каждое до 10-3.
В каких пределах с вероятностью 0,997 будет
лежать суммарная ошибка?
Пусть i -ошибка округления каждого слагаемого
3
«3σ»
M i 0 i
n
2
Yn i ~ N 0; 0,5 10
i 1
i ~ R 0,5 10 ; 0,5 10
ЦПТ
3
10
3
12
0,997 P Yn 0 3 Y
2
n
Yn 1,5 10 Y 0,015; 0,015
n
i
6
i 1

7.

Теоремы Муавра-Лапласа
Пусть имеет место схема испытаний Бернулли и
СВ X k ~ Ber p
Тогда СВ
Yn
n
X k ~ Bin n, p
k 1
Так как X k независимы и одинаково распределены
с м.о. m p и дисперсией pq,
2
то по ЦПТ СВ Yn асимптотически нормальна ,
mY np
Y npq
2
Yn np d
N 0, 1
n
npq
7

8.

Интегральная теорема Муавра-Лапласа
Пусть имеет место схема испытаний Бернулли и СВ
Yn ~ Bin n, p Тогда при достаточно больших n
Yn np
P
npq
b np a np
P a Yn b
npq npq
Условия
применимости (1):
np 3 npq 0
np 3 npq n
(1)
(2)
8

9.

Пример Известно, что левши составляют примерно 10%
населения. Какова вероятность того, что среди 160 человек
окажется от 10 до 20 левшей?
Y ~ Bin 160; 0,1
M Y np 16, D Y npq 14,4
Y npq 3,8
np 3 npq 16 3 3,8 4,6 0
np 3 npq 16 3 3,8 27,4 160
20 16
10 16
P 10 Y 20
3,8
3,8
1,05 1,58 0,34 0,45 0,79
9

10.

Локальная теорема Муавра-Лапласа
Пусть имеет место схема испытаний Бернулли и СВ
Yn ~ Bin n, p
Тогда при достаточно больших
1
1
P Yn k
e
2
npq
Условия
применимости (3):
n
2
k np
2npq
np 3 npq 0
np 3 npq n
(3)
(2)
1 10 16
1
0,11
P Y 10
f
f 1,58
3,8 3,8 3,8
3,810

11.

Центральная предельная
и ее следствия
Применение
теоремтеорема
Муавра-Лапласа
Bin 100, 0,5
np 50
npq 5
35;
65
Условия
применимости
Bin 100, 0,05
np 5
np 2
npq 2,18
1,54;
Bin 4, 0,5
11,54
npq 1
1; 4
np 3 npq 0
np 3 npq n
11