Числовые последовательности. Предел числовой последовательности и её сходимость

1. Числовые последовательности

Предел числовой
последовательности и её
сходимость

2.

Бесконечной числовой
последовательностью
называется числовая функция,
определённая на множестве
натуральных чисел.

3.

Способы задания последовательности:
1) В виде формулы – по номеру n-ого члена
an=2n
2) Рекуррентный (индуктивный) –
указывается правило, по которому можно вычислить
общий член последовательности через предыдущие и
задается несколько первых членов.
an=an-1+an-2
a1=3, a2=5,
3) Словесное описание последовательности

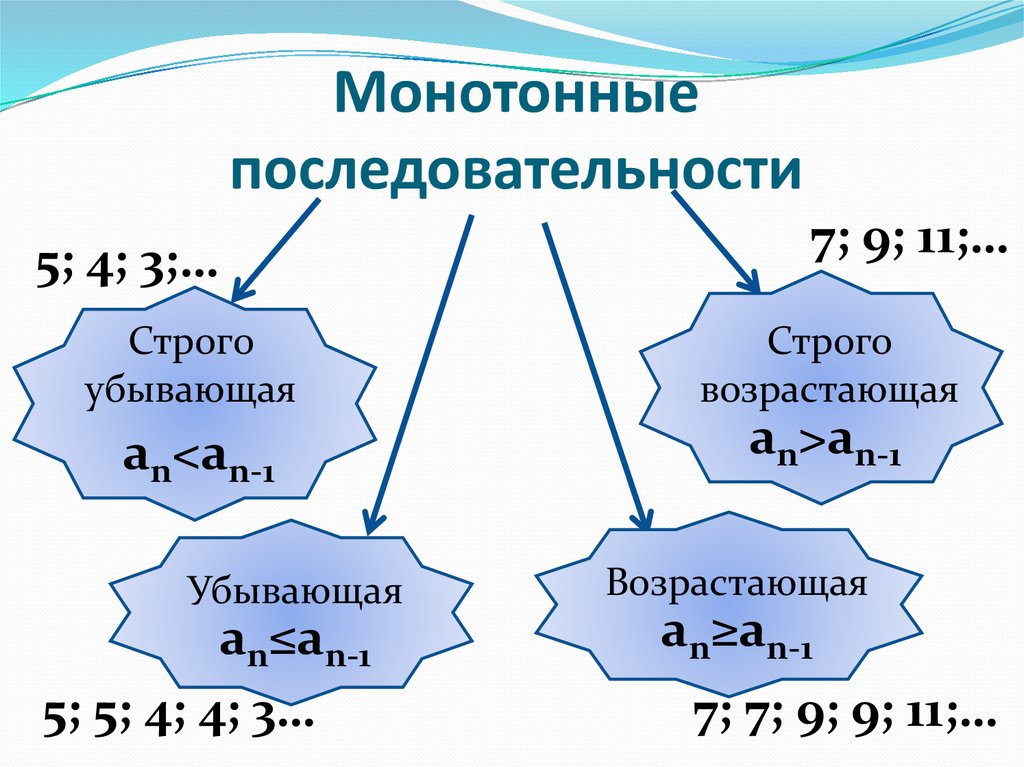
4. Монотонные последовательности

5; 4; 3;…
7; 9; 11;…
Строго
убывающая
Строго
возрастающая
an<an-1
an>an-1
Убывающая
an≤an-1
5; 5; 4; 4; 3…
Возрастающая
an≥an-1
7; 7; 9; 9; 11;…

5. Знакочередующаяся последовательность

an ( 1) 2n
n
a1 ( 1) 2 1 2
1
a2 4
a3 6
a4 8

6.

Последовательность an называется
ограниченной, если существуют такие точки
M и m, что для любого натурального n
выполняется неравенство: m≤an≤M
1
0 1
n
1 1 1
0 1; ; ; ;... 1
2 3 4
m 0 M 1
В противном случае последовательность
называется
неограниченной.

7.

Если существует точка М (m), и не существует
точка m (M), то последовательность
называется ограниченной сверху (снизу) и
неограниченной снизу (сверху).
0 2 1; 2; 4; 8; ...
n
- ограниченна снизу
3n 0;- 3; -12; - 27; ... 0
2
- ограниченна сверху

8. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.

Число а называют пределом числовой
последовательности, если для любого
положительного ε > 0 существует такое
натуральное N, что для каждого натурального
n ≥ N выполняется неравенство |an-a|<ε
Lim an a
n
a-ε
a
a+ε

9.

Последовательность, имеющая предел, называется
сходящейся, а не имеющая предел – расходящейся.
ТЕОРЕМА: Необходимое условие
существования предела последовательности.
Если последовательность имеет предел, то она
ограничена.
ТЕОРЕМА : Всякая сходящаяся последовательность
имеет один предел.
ТЕОРЕМА : Если числовая последовательность
монотонна и ограничена, то она имеет предел.

10. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.

Бесконечно малой (бм) величиной называется
такая переменная величина, которая в процессе своего
изменения становится и в дальнейшем остается по
модулю меньше любого наперед заданного
положительного числа, как бы мало оно ни было.
Lim an 0
n

11. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ.

Последовательность называется бесконечно
большой (бб), если для каждого положительного
числа А найдется такое натуральное число N, что
для любого n >N выполняется неравенство: |an|>A
Lim an
n

12. Свойства бесконечно малой.

Сумма и произведение конечного числа
бесконечно малых последовательностей есть
бесконечно малая последовательность.
Произведение константы на бесконечно малую
последовательность есть бесконечно малая
последовательность.
x – бесконечно малая, то 1/x – бесконечно большая
и наоборот (x – бб → 1/x – бм).
Если
x 0
то
1
x
Если
x
то
1
0
x

13. Свойства пределов.

1) Lim an bn cn Lim an Lim bn Lim cn
n
n
n
2) Lim an bn Lim an Lim bn
n
n
n
n
2* ) Lim C an C Lim an
an
an Lim
3) Lim n , если Lim bn 0
n b
n
bn
n Lim
n
k
4) Lim an
n
Lim an
n
5) Lim k an k Lim an
n
n
k
n
n

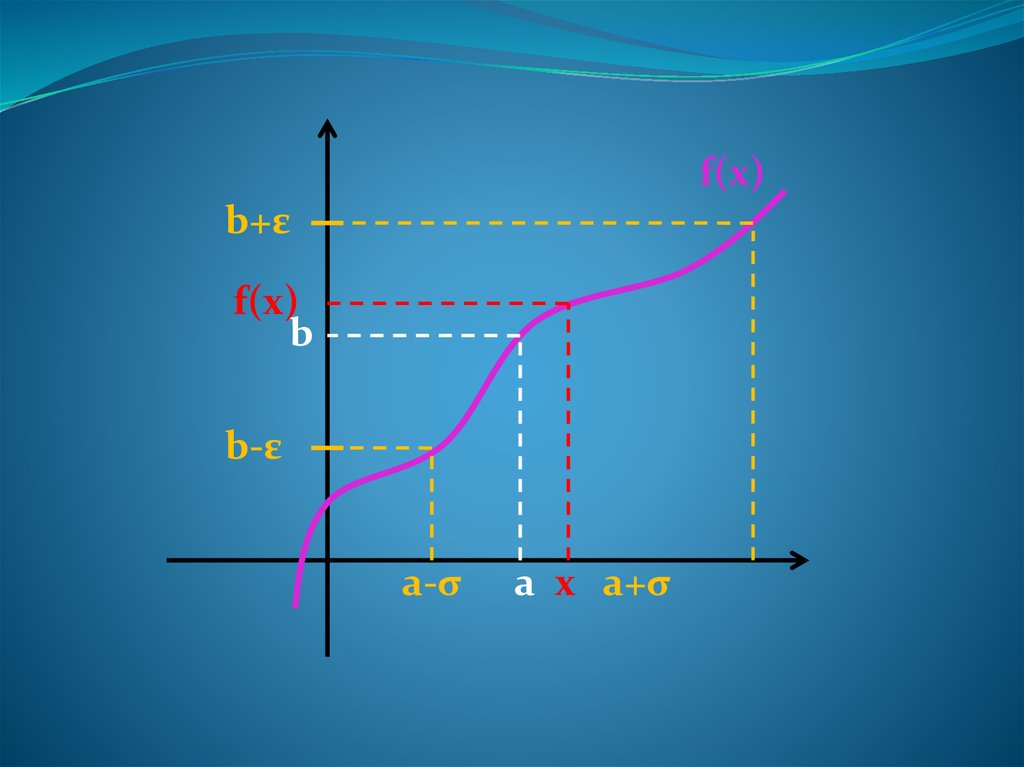
14. Предел функции

Число b есть предел функции f(x) при x→a
если, какова бы ни была ε-окрестность точки
b, найдется такая σ-окрестность точки а, что
для любого значения x≠a и принадлежащего
σ-окрестности точки а, значение f(x) ,будет
принадлежать ε-окрестности точки b.
Lim f ( x) b
x a

15.

f(x)
b+ε
f(x)
b
b-ε
a-σ
a x a+σ

16. Теоремы о пределах

1) Lim f1 ( x) f 2 ( x) f 3 ( x) Lim f1 ( x) Lim f 2 ( x) Lim f 3 ( x)
x a
x a
x a
Lim fa1 (nx
) bfn2 ( x)c n Lim
f1 ( xa)n Lim
f 2 (b
x)n Lim cn
12) Lim
Lim
Lim
x a
x a
x a
n
n
n
x a
n
C f ( x) C Lim f ( x)
2* ) Lim
x a
x a
f ( x)
Lim
f ( x)
Теоремы
2-5
см
свойства
3) Lim
, если Lim f ( x) 0
f ( xпределов
) Lim f ( x) последовательности
x a
1
x a
2
x a
1
2
4) Lim [ f ( x)]n [ Lim f ( x)]n
x a
x a
x a
5) Lim n f ( x) n
x a
Lim f ( x)
x a
6) Правило Лопиталя:
0
0
2
Lim
x a
f1 ( x)
f1 ( x)
Lim
f 2 ( x)
x a
f 2 ( x)

17. Односторонние пределы.

Правый предел
Левый предел
Lim f ( x) Lim f ( x) f (a 0) Lim f ( x) Lim f ( x) f (a 0)
x a 0
x a 0
x a
x a
a
При a=0
x a
x a
a
Левый предел
Правый предел
Lim f ( x) Lim f ( x) f ( 0)
Lim f ( x) Lim f ( x) f ( 0)
x 0
x 0
x 0
x 0
x 0
x 0

18.

Найти предел функции при x →1
x 1, если x 1
f ( x)
2 x 1, если x 1
Левый предел:
Lim f ( x) Lim ( x 1) 0
Правый предел:
Lim f ( x) Lim (2 x 1) 3
x 1 0
x 1 0
x 1
x 1
x 1
x 1

19. Замечательные пределы

Две бесконечно малые называются
эквивалентными, если предел их
отношения равен единице.
Эквивалентные бесконечно малые
можно заменять одна на другую.

20. Замечательные пределы

tgx
sin x
1
1) Lim
1 Lim
x 0 x
x 0
x
y
β
α
2) Lim 1 e
y
y
α
β
1
3) Lim 1 e
n
n
4) Lim 1 y
y 0
e
y 0
e x 1
6) Lim
1
x 0
x
Ln(1 x)
7) Lim
1
x 0
x
n
1
y
5) Lim 1 y e
1
y
(1 x) k 1
8) Lim
k
x 0
x

21. Эквивалентные функции при x → 0

sin x ~ x
tg x ~ x
arcsin x ~ x
arctg x ~ x
ex – 1 ~ x
ln (1 + x) ~ x
(1 + x)k – 1 ~ k x

22.

Если предел отношения двух бесконечно малых
равен некоторому числу k, отличному от единицы,
то эти бесконечно малые называются
одинаковыми или бесконечно малыми одного
порядка малости.
Lim k 1, k - const
Если предел отношения двух бесконечно
малых равен нулю, то в числителе
бесконечно малая более высокого порядка,
чем в знаменателе.

23. Непрерывная функция

ТЕОРЕМА: Функция не может иметь двух
различных пределов в точке.
Функция является непрерывной в точке а,
если она имеет предел равный значению
функции в этой точке.
Lim f ( x) f (a )
x a

24.

Функция, непрерывная в каждой точке промежутка
называется непрерывной на всём промежутке.
Точки, в которых нарушается непрерывность функции,
называются точками разрыва этой функции.
Функция, имеющая правый (левый) предел,
непрерывна справа (слева).
Если функция имеет конечный правый или левый предел
в точке разрыва, то это – точка разрыва первого рода
(все остальные – второго рода).

25. Свойства непрерывных функций

, Сумма (произведение) конечного
числа непрерывных в точке а функций есть
непрерывная в этой точке функция.
Отношение двух функций,
непрерывных в точке а есть непрерывная в этой
точке функция, если значение функции, стоящей в
знаменателе в точке а отлично от нуля.