Корреляционный анализ для линейных моделей

1. 1. Корреляционный анализ

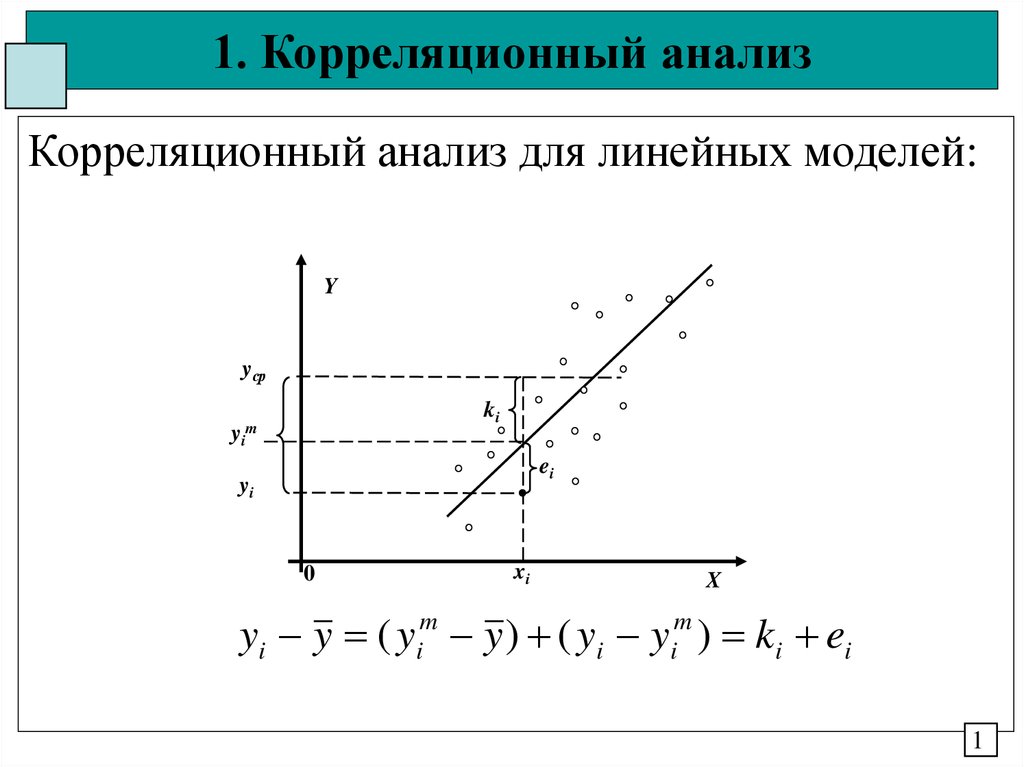
Корреляционный анализ для линейных моделей:
Y
yср
ki
yim
ei
yi
0
xi
X
yi y ( yim y ) ( yi yim ) ki ei
1

2. 1. Корреляционный анализ

[( yi y ) 2 ] [k 2 ] 2[k e] [e 2 ]
y y 2 k 2 e2
y y 2 - мера общего разброса переменной у относительно
средней;
[( yim y ) 2 ] [k 2 ] - мера разброса модели переменной у относительно
средней (часть объясненная регрессией);
[( yi yim ) 2 ] [e 2 ] - мера остаточного
(не объясненного)
переменной у относительно модели
разброса
2

3. 1. Корреляционный анализ

Доля объясненного разброса
k 2
2
R
y y 2
коэффициент детерминации
2
k 2
e 2
e
2
1
R
2
2
y y y y
y y 2
2
e
2
R 1
y y 2
все минус необъясненная
доля
3

4. 1. Корреляционный анализ

Коэффициент детерминации:
- мера в какой степени найденная линия лучше
для объяснения поведения зависимой
переменной Y чем горизонтальная прямая,
проходящая через среднее значение;
- процент объясненных данных;
- совпадает с квадратом парного
(множественного) коэффициента корреляции для
линейной функции.
4

5. 1. Корреляционный анализ

2
2
[( yi y ) 2 ]
[
k
]
[
e
]
2
2
2
Y
k e
n
n
n
- дисперсия результирующего признака равна:
факторная дисперсия плюс остаточная дисперсия
R
1
I Y2 X - корреляционное соотношение
2
2
k
2
Y
2
e
2
Y
ei yi y
m
i
5

6. 1. Корреляционный анализ

n-мерное линейное уравнение:
yim a1 x1 ... an 1 xn 1 an
дисперсии:
k2 D f a T K a
~ ~
T
~
De a K a
2
e
Индекс корреляции (коэффициент детерминации)
I
2
Y X
T
a Ka
2
y
1
T
a Ka
y2
6

7. 1. Корреляционный анализ

Другие виды коэффициентов корреляции:
- множественный
Дисперсии
1
De ~ 1 ;
K nn
~
DY K nn
Из коэффициента детерминации
De
1
2
Rn|... 1
1
Dy
K nn K nn 1
Для любого i – множественный (совокупный)
коэффициент. Суть.
7

8. 1. Корреляционный анализ

- частный (вклад в множественный каждого)
2
- факторная дисперсия при всех переменных
y1...m
2
y1...m 1
- факторная дисперсия без одной переменной
2
y (1...m 1)
- остаточная дисперсия без одной переменной
y21...m y21...m 1
y21...m y21...m 1
Rym (12...m 1)
2
y (1...m 1)
y2 y21...m 1
8

9. 1. Корреляционный анализ

Суть коэффициента.
При наличии ковариационной матрицы (матрицы
моментов):
rij|...
Kij 1
Kii 1 K jj1
Элементы анализа и выбора модели на основе
введенных коэффициентов.
Контроль для трех рядов.
9

10. 1. Корреляционный анализ

-коэффициент корреляции рангов Спирмена.
Необходимость. Ранжировка. Порядковый номер – ранг.
Качество А – ранги A1 , A2 ,..., An В – B1 , B2 ,..., Bn
разность между ними Ak Bk d k - мера тесноты
соответствия между качествами А и В.
Нуль - соответствие полное. По парному:
a b
A (n 1) / 2 B (n 1) / 2
r
a b
A (n 1) / 2 B (n 1) / 2
k
k
12
k
2
k
2
k
1
k
k
k
6 d 2
n3 n
Свойства, использование
10

11. 1. Корреляционный анализ

-коэффициент ассоциации (тетрахорический
показатель 2 групп Д. Юла )
2 признака (например, появились – не появились) и две
категории в каждом признаке (например,
положительные значения – отрицательные значения). По
результатам подсчетов составляется 2 2 таблица вида
категория
признак
А(да)
В(нет)
1(+)
2(–)
a
c
b
d
средний размер связи по Юлу между категориями 1 и 2
по признакам А и В будет
ad cb
Ka
ad cb
11