Похожие презентации:
Кристаллофизикалық координат жүйесі
1.
Қатты дене физикасы мен материалтану кафедрасыКристаллофизика негіздері (3-4 дәрістер)
Кристаллофизикалық координат жүйесі
Нүктелік симметрия элементтерін матрица түрінде көрсету
Кеңістік фигуралардың нүктелік симметрия топтары туралы
ұғым. Топтық әсердің заңдары
Нүктелік
симметрия
элементтерінің
теоремаларды матрица арқылы дәлелдеу
үйлесуі
туралы
Ерекше немесе жекелік бағыттар
Кристалдың нүктелік симметрия топтары (кластары). 32
нүктелік симметрия тобын шығару
Кристаллографиялық
сингониялар
категориялар,
Кристаллографиялық номенклатура
жүйелер
және
2.
Қатты дене физикасы мен материалтану кафедрасыСимметриялық
түрлендірулерді
талдау
үшін
қолданатын
тікбұрышты координат жүйелері оң немесе сол болуы мүмкін.
Оларды ажырату үшін координаттардың бастапқы нүктесінде Х3
осіне сүйеніп тұрған адамды қарастыру керек. Егер оның оң
жағында Х1 осі ал сол жағында Х2 осі орналасқан болса, онда бұл оң
координат жүйесі болады. Егер керісінше болса, оның оң жағында
Х2 осі, ал сол жағында Х1 осі болса, онда бұл сол координат жүйесі
болады.
Оң координат жүйесі
Сол координат жүйесі
Кристаллофизикалық координат жүйелері
3.
Қатты дене физикасы мен материалтану кафедрасыСимметриялық түрлендірулер ескі және жаңа координат осьтерінің
арасындағы бұрыштардың косинустары арқылы табылады. Қысқаша
белгілеу енгізейік:
С11 = cos(X1'X1),
С21 = cos(X2'X1),
С31 = cos(X3'X1),
С12 = cos(X1'X2),
С22 = cos(X2'X2),
С32 = cos(X3'X2),
С13 = cos(X1'X3),
С23 = cos(X2'X3),
С33 = cos(X3'X3).
Бірінші орынға жаңа координат жүйенің, ал екінші орынға ескі
жүйенің индексі қойылады.
Бағыттаушы косинустарды матрица түрінде келтіру қолайлы болады:
X1
X2
X3
X1'
c11
c12
c13
X2'
c21
c22
c23
X3'
c31
c32
c33
немесе қысқаша
c11
c12
c13
c21
c22
c23
c31
c32
c33
4.
Қатты дене физикасы мен материалтану кафедрасыБағыттаушы косинустар матрицасы төмендегі қасиеттерге ие болады:
1. Жолдар немесе бағаналар квадраттарының сомасы бірге тең болады.
2. Қос жолдар немесе бағаналардың көбейтіндісінің сомасы нольге тең.
3. Матрица детерминанты:
|Cij| = С11С22С33 + С12С23С31 + С13С21С32 – С13С22С31 – С11С23С32 –
– C12C21C33 = +1
оң жүйеден оң жүйеге және сол жүйеден сол жүйеге өткенде;
|Cij| = С11С22С33 + С12С23С31 + С13С21С32 – С13С22С31 – С11С23С32 –
– C12C21C33 = – 1
оң жүйеден сол жүйеге және керісінше өткенде.
4. Матрицаның кез келген элементі келесі қатынастан табылады:
Cij = (–1)i + j Aij|Cij|,
Aij – i бағанасын және j жолын сызып тастағанда шығатын қосымша
минор.
5.
Қатты дене физикасы мен материалтану кафедрасыРеті 2-ші ось және осы ось бойымен өтетін
mI, mII екі өзара перпендикуляр симметрия
жазықтықтарының симметриялық түрлендіруін қарастырайық.
Түрлендірулер басында ескі және жаңа
координат жүйелері бір болады.
Тождестволық операция нәтижесінде (1 ось) жаңа координат жүйесі
360° айналып бастапқы қалпына оралады. Осындай түрлендіру
нәтижесінде бағыттаушы косинустар келесі түрге келеді:
С11 = cos(0) = 1,
С21 = cos(90) = 0,
С31 = cos(90) = 0,
С12 = cos(90) = 0,
С22 = cos(0) = 1,
С32 = cos(90) = 0,
Бағыттаушы косинустар матрицасы келесі
түрде болады:
С13 = cos(90) = 0,
С23 = cos(90) = 0,
С33 = cos(0) = 1.
1 0 0
0 1 0
0 0 1
6.
Қатты дене физикасы мен материалтану кафедрасыХ2 (ось 2) осін 180° айналдыру
симметриялық түрлендіруін жасайық. Бұл
жағдайда X2' осі Х2 осінің орнына келеді, X3'
осі –Х3 осінің бойымен бағыталады, ал Х1'
осі –Х1 осінің бойымен бағыталады.
Онда бағыттаушы
косинустар матрицасы
келесі түрде болады:
1 0
0
0
1
0
0
0 1
mI жазықтығында шағылу нәтижесінде X2' осі
Х2 осінің, Х1' осі Х1 осінің, ал Х3' осі –Х3 осінің
бойымен бағыталады.
Бағыттаушы косинустар
матрицасы келесі түрде
болады:
1 0
0
0 1
0
0 0 1
7.
Қатты дене физикасы мен материалтану кафедрасыmII жазықтығында шағылу нәтижесінде Х3'
осі Х3 осінің, X2' осі X2 осінің, ал X1' осі –X1
осінің бойымен бағыталады.
Онда бағыттаушы
косинустар матрицасы
келесі түрде болады:
1 0 0
0
1 0
0
0 1
Кеңістік фигуралардың көбісі бірнеше симметриялық түрлендіру
көмегімен бейнеленетін күрделі симметрияға ие болады. Олардың
қатар әсерінің себебінен жаңа симметриялық түрлендірулер
туындайды. Мұндай кезде симметриялық түрлендірулер «қосылады»
дейді. Симметриялық түрлендірулердің «қосылуын» симметрия
элементтерін қолдана отырып геометриялық әдіспен көрсету оңай.
«Қосылу» жоғарыда аталған теоремаларға негізделеді.
8.
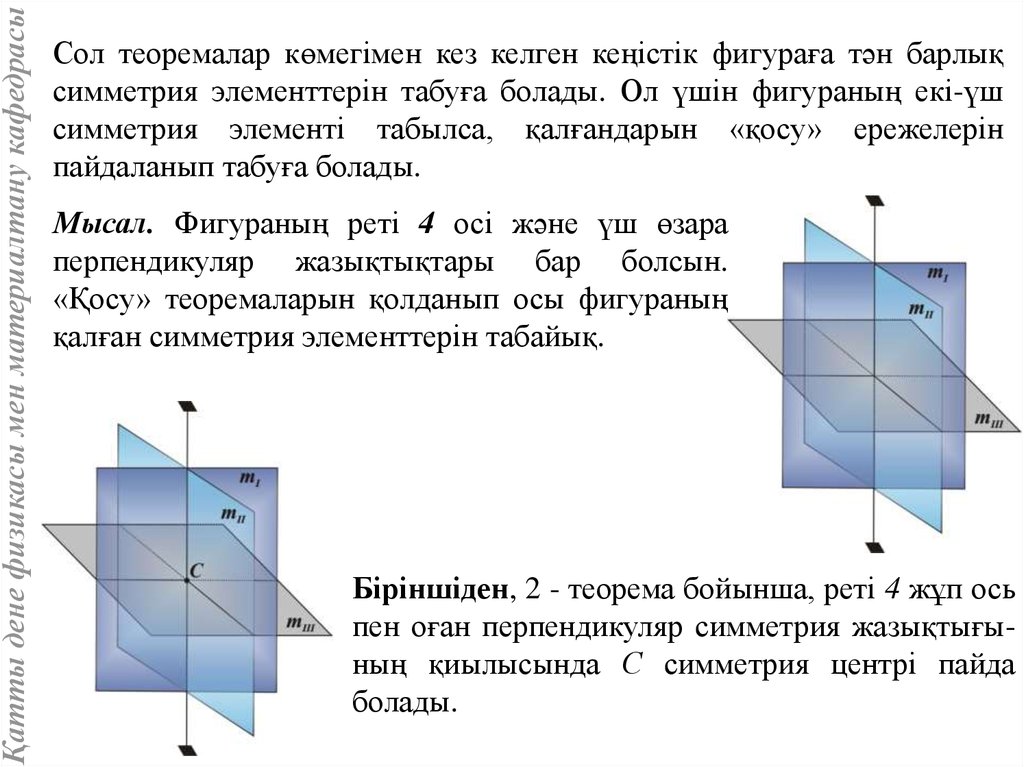
Қатты дене физикасы мен материалтану кафедрасыСол теоремалар көмегімен кез келген кеңістік фигураға тән барлық
симметрия элементтерін табуға болады. Ол үшін фигураның екі-үш
симметрия элементі табылса, қалғандарын «қосу» ережелерін
пайдаланып табуға болады.
Мысал. Фигураның реті 4 осі және үш өзара
перпендикуляр жазықтықтары бар болсын.
«Қосу» теоремаларын қолданып осы фигураның
қалған симметрия элементтерін табайық.
Біріншіден, 2 - теорема бойынша, реті 4 жұп ось
пен оған перпендикуляр симметрия жазықтығының қиылысында С симметрия центрі пайда
болады.
9.
Қатты дене физикасы мен материалтану кафедрасыЕкіншіден, 4-ші теорема бойынша реті 4-ші ось
оның ретіне тең жазықтықтар санын тудырады,
б.а. 4 жазықтық пайда болады.
Үшіншіден, 1-ші теорема бойынша, өзара
перпендикуляр симметрия жазықтықтарының
қиылысында реті 2-ші осьтер пайда болады.
Сонымен, бұл фигура келесі симметрия элементтерінің жинағынан тұрады: 4
ось, төрт 2 осьтер, бес m симметрия жазықтығы және С симметрия центрі.
Қысқаша бұл симметрия элементтерінің жинағы келесі түрде жазылады:
424т5С.
Бастапқы берілген симметрия элементтері 4 және m3 тудырушы элементтер
деп аталады. Симметрия формуласына тек соларды жазады. Онда бұл
фигураның симметрия формуласы 4/mmm болады.
10.
Қатты дене физикасы мен материалтану кафедрасыКез
келген
кеңістік
фигураның
барлық
симметриялық
түрлендірулерінің жинағы математика тұрғысынан топ құрады.
Элементер жинағы топ құру үшін келесі заңдардың орындалуы қажет:
1. Кеңістік фигураның екі симметриялық түрлендіруінің көбейтіндісі
осы фигураның симметриялық түрлендіруі болып табылады.
2. Терімділік заңы орындалады – үш симметриялық түрлендірудің
көбейтіндісінде олардың орындарын ауыстыруға болады .
3. Берілген кеңістік фигураның кез келген симметриялық
түрлендіруінің бірлік симметриялық түрлендіруге көбейтіндісі осы
симметриялық түрлендіруге тең болады.
4. Кеңістік фигураның әрбір симметриялық түрлендіруіне кері
симметриялық түрлендіру табылады, ал олардың көбейтіндісі
бірлік симметриялық түрлендіруге тең болады.
11.
Қатты дене физикасы мен материалтану кафедрасыМысал.
Тікбұрышты
пирамиданың
симметриялық түрлендірулері топтық
заңдарға бағынатынын тексеріп көрейік.
Бұл фигураның симметриясы келесі
түрлендірулермен
сипатталады:
тождестволық (1 ось), 180° бұрышына
айналу (2 ось) және mI и mII
жазықтықтардан
шағылулар.
Пирамиданың
бұрыштарын
суретте
көрсетілгендей белгілейік.
Топтың бірінші қасиетін тексеру үшін
екі операцияны ретімен орындайық:
180° айналу және mI жазықтығынан
шағылу.
Осы
екі
операцияның
көбейтіндісі
mII
жазықтығынан
шағылуына тең болады, ал бұл
симметриялық түрлендіру осы топқа
жатады.
mm2 тобының топтық заңдарының
орындалуын бейнелетін симметриялық
түрлендірулер.
12.
Қатты дене физикасы мен материалтану кафедрасыТоптық көбейту заңын келесі түрге келтіруге болады:
1
2
mI
mII
1
1
2
mI
mII
2
2
1
mII
mI
mI
mI
mII
1
2
mII
mII
mI
2
2
Әр ұяшықта вертикал және горизонтал
жолдардағы симметриялық түрлендірулердің
көбейтіндісінің нәтижесі келтірілген.
Сонымен, кеңістік фигуралардың симметриялық түрлендірулері топтар
құрады. Бұл топтар нүктелік симметрия топтары деп аталады, өйткені кез
келген түрлендіруде координата басындағы бір нүкте қозғалмайтын болады.
Симметрия элементтерінің жоғарыда көрсетілген график түріндегі қосуын
матрицалық әдіспен жасауға болады. Симметрия элементтерінің үйлесуі
сәйкесті матрицалардың көбейтіндісі арқылы табылады. Екі матрицаның
көбейтіндісі төмендегідей анықталады:
a11
akl bli d ki a21
a
31
бұл жерде
a12
a22
a32
d ki akl bki
a13 b11 b12 b13 d 11 d12 d13
a23 b21 b22 b23 d 21 d 22 d 23
a33 b31 b32 b33 d 31 d 32 d 33
13.
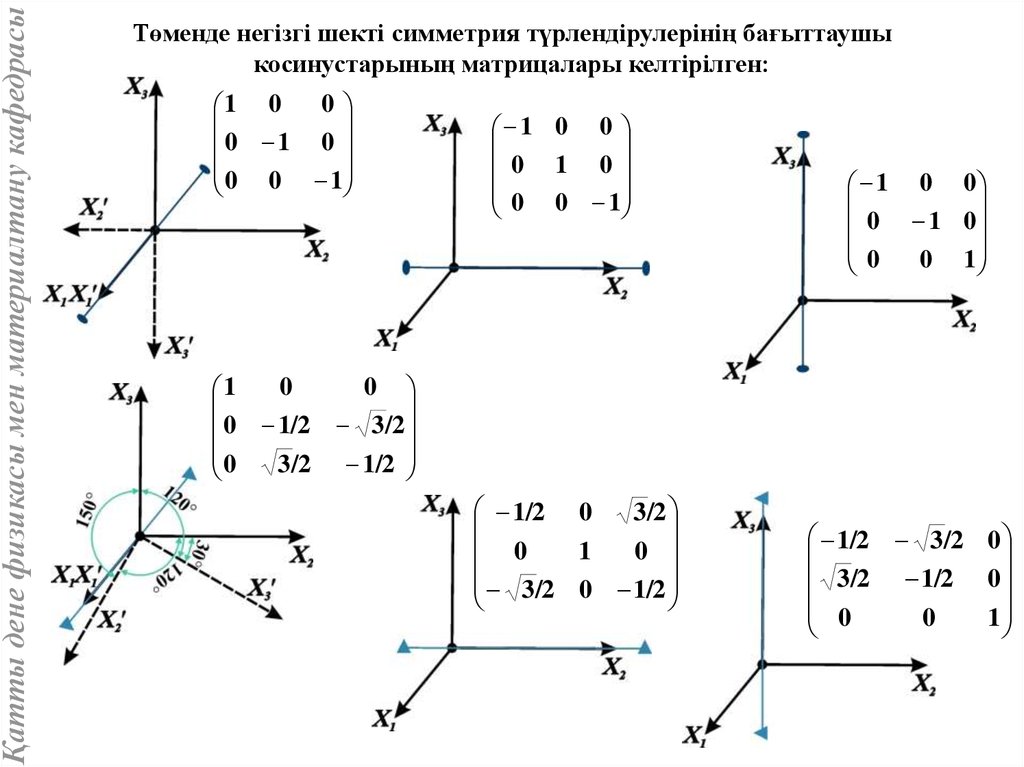
Қатты дене физикасы мен материалтану кафедрасыТөменде негізгі шекті симметрия түрлендірулерінің бағыттаушы
косинустарының матрицалары келтірілген:
0
1 0
0
1
0
0 0 1
1 0 0
0
1
0
0 0 1
1 0 0
0 1 0
0
0 1
0
0
1
0 1/2 3 /2
0
3 /2 1/2
1/2 0
3 /2
1
0
0
3
/2
0
1/2
1/2 3/2 0
3/2 1/2 0
0
0
1
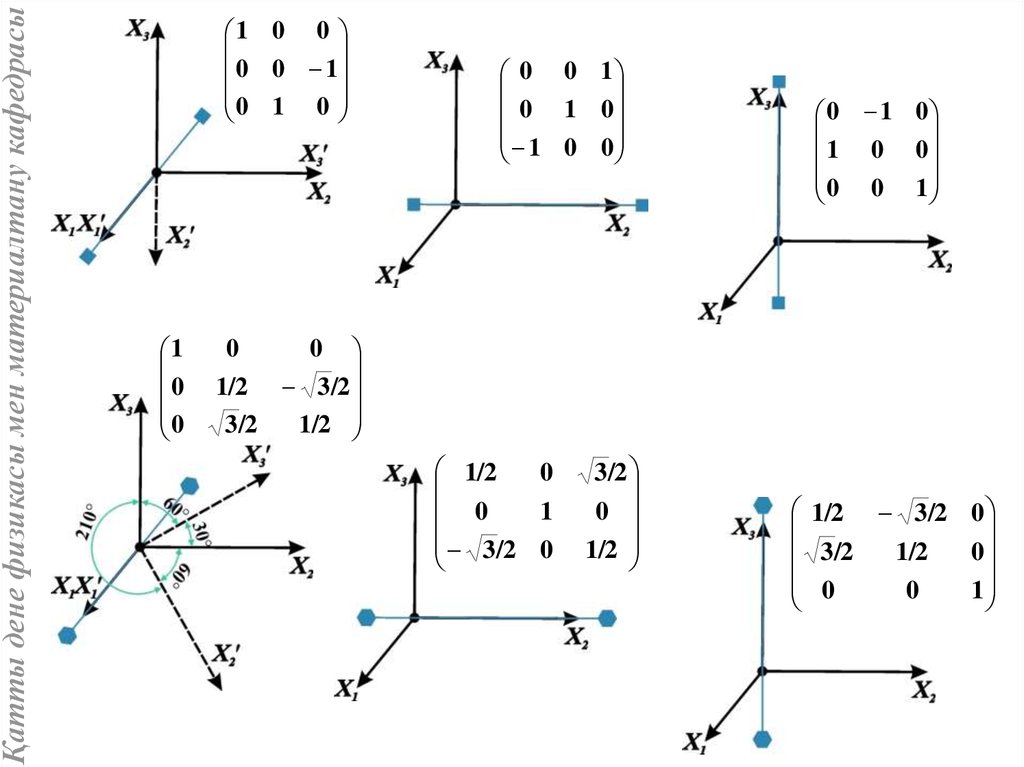
14.
Қатты дене физикасы мен материалтану кафедрасы1 0 0
0
0
1
0 1 0
1
0
0
0 0 1
0
1
0
1 0 0
0 1 0
1
0
0
0 0 1
1/2 3 /2
3 /2
1/2
0
0
1/2
0
1
0
3/2 0
3/2
0
1/2
1/2 3/2 0
1/2
0
3/2
0
0
1
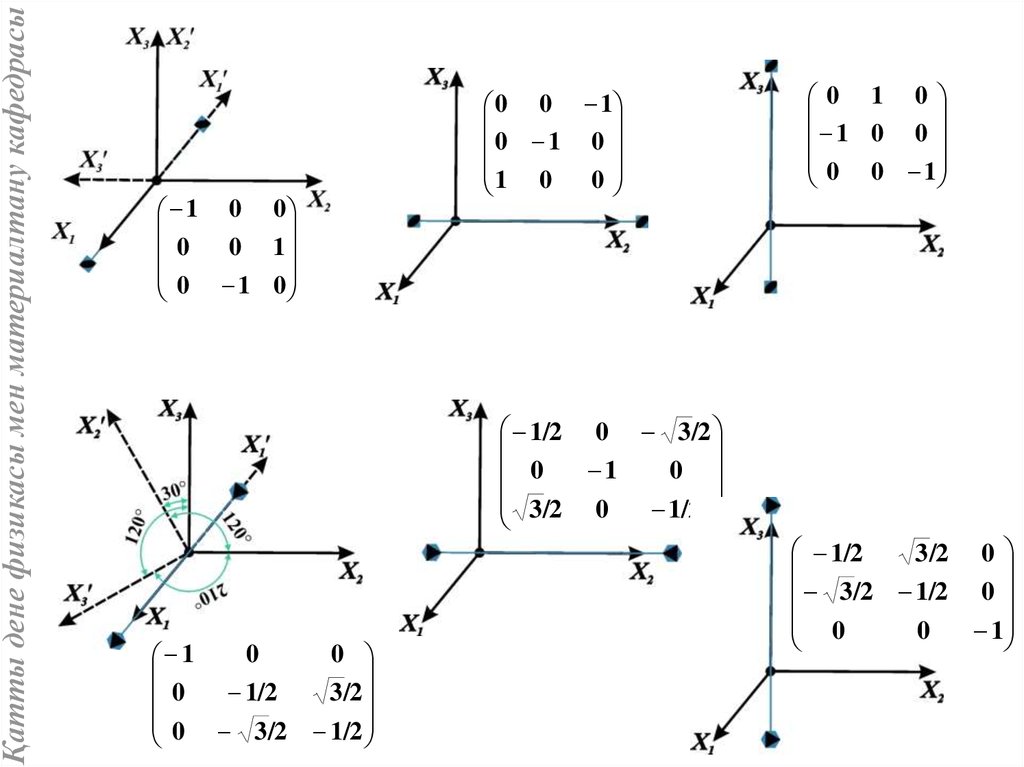
15.
Қатты дене физикасы мен материалтану кафедрасы1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1/2
0 3 /2
1
0
0
3
/2
0
1/2
0
1
1/2
0
0 3 /2
0
3 /2
1/2
1 0 0
0 1 0
0 0 1
1/2
3 /2
0
3 /2
1/2
0
0
0
1
16.
Қатты дене физикасы мен материалтану кафедрасы1 0 0
0
0
1
0 1 0
0 0 1
0
1
0
1 0
0
1/2 0 3 /2
1
0
0
3
/2
0
1/2
0
0
1
1/2
3 /2
0
0 3 /2 1/2
0 1 0
1 0 0
0 0 1
1/2
3 /2 0
3 /2 1/2 0
0
0
1
17.
Қатты дене физикасы мен материалтану кафедрасыМысал. 2-ші теореманы матрицалық әдіспен дәлелдейік. Х2 параллель
2 симметрия осінің және перпендикуляр m(010) жазықтығының
матрицаларын көбейтіп:
1 0 0
1 0 0
m(010) 0 1 0
2[010] 0 1 0
0 0 1
0 0 1
Симметрия центрінің матрицасын табамыз:
1 0 0
1 0 1 0
0 0 1
Сонымен 2-ші теореманың матрицалық әдіспен дәлелдеуі келесі түрде
жазылады:
1 0 0 1 0 0 1 0 0
0 1 0 0 1 0 0 1 0 1
0 0 1 0 0 1 0 0 1
Осылай симметрия элементтерінің үйлесуі туралы қалған
теоремаларды дәлелдеуге және кристалдардың 32 симметрия классын
шығаруға болады.
18.
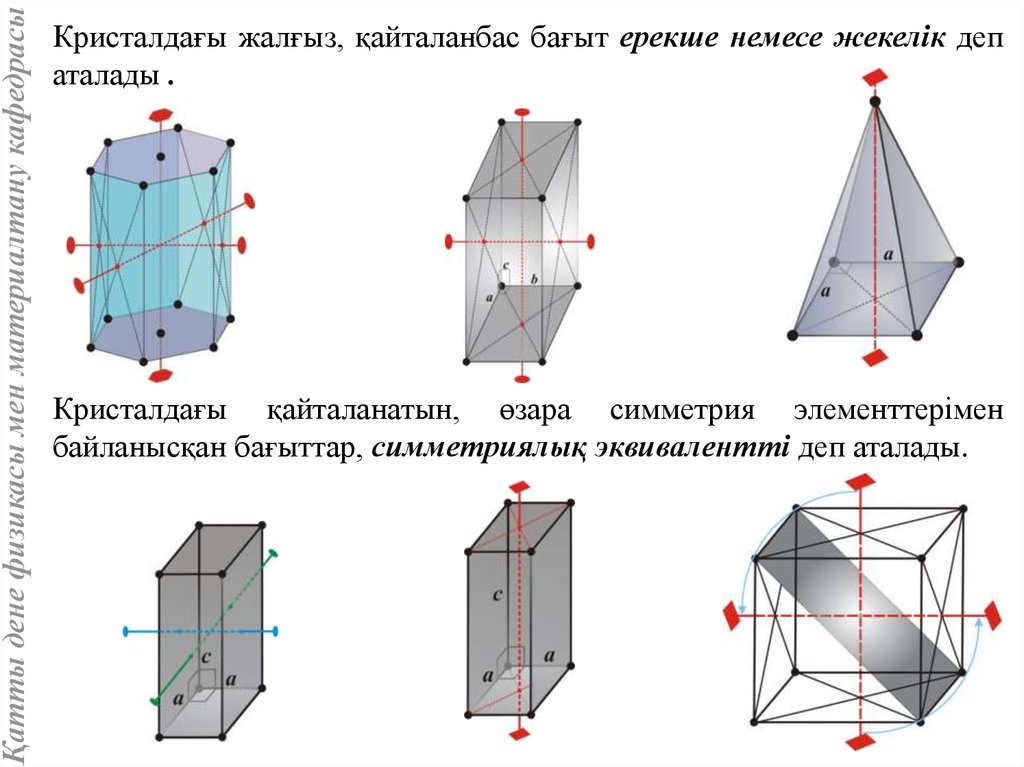
Қатты дене физикасы мен материалтану кафедрасыКристалдағы жалғыз, қайталанбас бағыт ерекше немесе жекелік деп
аталады .
Кристалдағы қайталанатын, өзара симметрия элементтерімен
байланысқан бағыттар, симметриялық эквивалентті деп аталады.
19.
Қатты дене физикасы мен материалтану кафедрасыКристалдың нүктелік симметрия топтары (кластары)
Идеал кристалдық көпқырлықтың симметрия операцияларының
көптігі, б.а. оны өз қалпына келтіретін түрлендірулері кристалдың
симметрия классын немесе нүктелік симметрия тобын құрады.
Топқа кіретін әртүрлі симметрия операцияларының саны топтың
реті деп аталады.
Халықаралық символикада нүктелік симметрия топтары келесі түрде
белгіленеді: п – реті n-ші симметрия осі (п = 2, 3, 4, 6), n – реті n-ші
инверсиялық симметрия осі, т – симметрия жазықтығы, пт – реті nші симметрия осі және оның бойымен өтетін n симметрия
жазықтықтары; п/т – реті п симметрия осі және оған перпендикуляр
симметрия жазықтығы; егер п жұп болса, онда 3-ші теорема бойынша
қосымша симметрия центрі бар болады; п2 – реті п-ші симметрия осі
және оған перпендикуляр реті екінші п симметрия осьтері; п/ттт –
реті n-ші симметрия осі және оған параллель және перпендикуляр т
жазықтықтар.
20.
Қатты дене физикасы мен материалтану кафедрасыКристалдың барлық нүктелік симметрия топтарын 1820 ж. неміс
минералогия профессоры И. Гессель анықтаған. Олардың саны 32.
Бірақ бір жағынан бұл нәтиже қолайсыз түрде берілген, ал екіншіден
Гессель мақаласы қолға сирек түсетін басылымда шыққан себебтен
оған ғылыми қауым назар аудармады.
1867 ж. Гессельге тәуелсіз 32 нүктелік симметрия тобын Ресей
академигі, Артиллерия академиясының профессоры, қызығушыкристаллограф, генерал А.В. Гадолин шығарып анықтады.
32 симметрия классын шығару үшін бір нүктеде қиылысатын
кристаллографиялық симметрия элементтерінің барлық мүмкін
терулерін қарастыру керек. Ол үшін кез келген бастапқы тудырушы
симметрия элементін алып оған кезегімен тудырушы элемент ретінде
қалған барлық симметрия элементтерін қосады. Теоремалардың
негізінде екі тудырушы симметрия элеметтерінің терулерінен туынды
симметрия элементтері шығарылады.
21.
Қатты дене физикасы мен материалтану кафедрасыЕрекше бағыттары бар кристалдар
Тудырушы симметрия элементі ретінде ерекше бағыт бойымен өтетін
симметрия осін алып оған суретте көрсетілгендей басқа симметрия
элементтерін қосайық.
22.
Қатты дене физикасы мен материалтану кафедрасыТек бір симметрия элементі бар кластар қарапайым симметрия
кластары болып табылады, атап айтқанда, ерекше бағыт бойымен
өтетін реті n-ші айналу осі
Қарапайым кластар
Әр оське симметрия центрін қосып және 2-ші теореманы қолданып
центрлік кластарын аламыз
23.
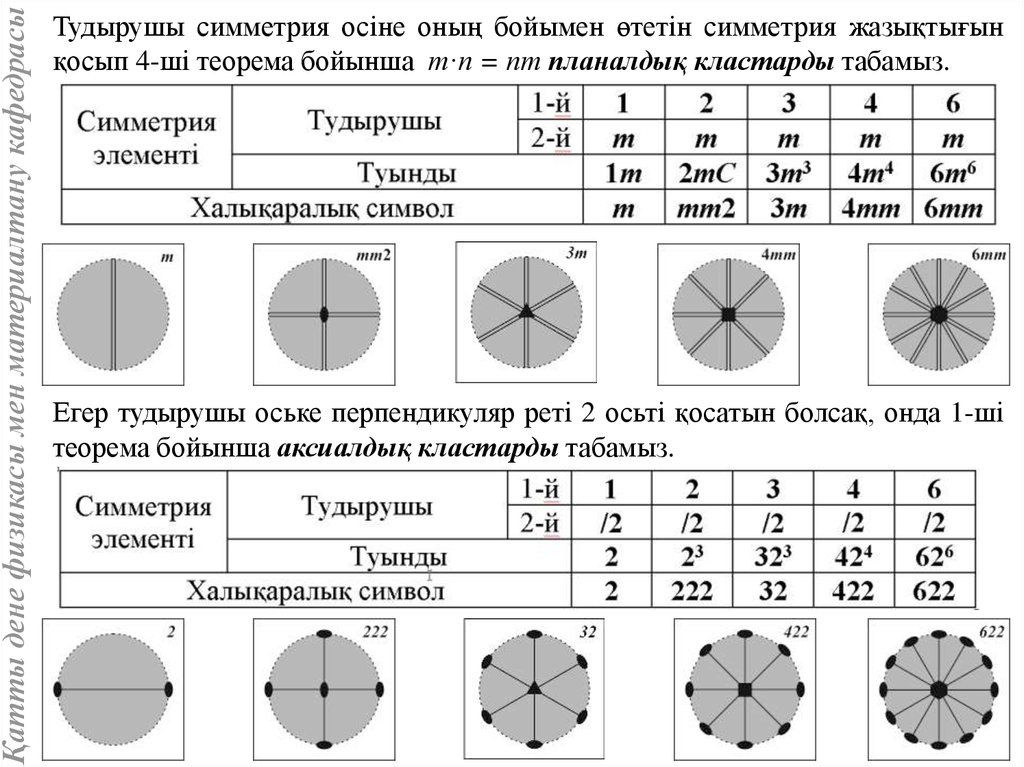
Қатты дене физикасы мен материалтану кафедрасыТудырушы симметрия осіне оның бойымен өтетін симметрия жазықтығын
қосып 4-ші теорема бойынша т·п = пт планалдық кластарды табамыз.
Егер тудырушы оське перпендикуляр реті 2 осьті қосатын болсақ, онда 1-ші
теорема бойынша аксиалдық кластарды табамыз.
24.
Қатты дене физикасы мен материалтану кафедрасыТудырушы симметрия осіне көлденең жазықтық қосылған кезде
инверсиялық-қарапайым класс пайда болады.
Тудырушы сииметрия осіне симметрия центрі, параллель
жазықтықтар және реті 2-ші перпендикуляр осьтері қосылған кезде
планаксиалдық (аксиал-центрлік) класс пайда болады.
25.
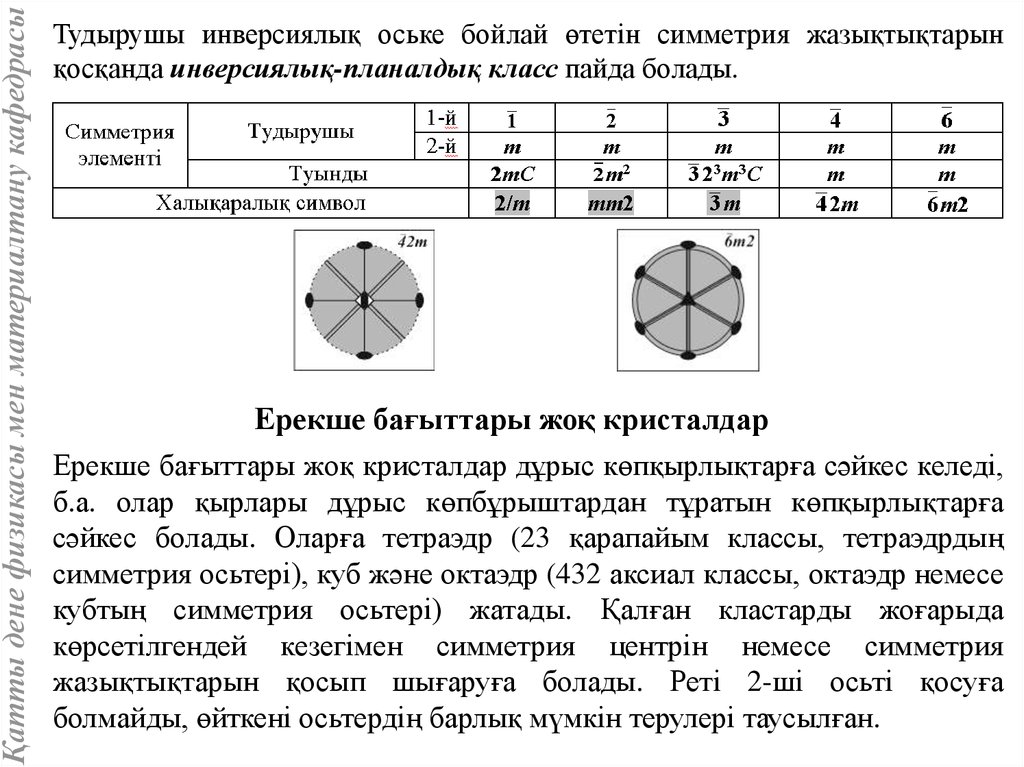
Қатты дене физикасы мен материалтану кафедрасыТудырушы инверсиялық оське бойлай өтетін симметрия жазықтықтарын
қосқанда инверсиялық-планалдық класс пайда болады.
Ерекше бағыттары жоқ кристалдар
Ерекше бағыттары жоқ кристалдар дұрыс көпқырлықтарға сәйкес келеді,
б.а. олар қырлары дұрыс көпбұрыштардан тұратын көпқырлықтарға
сәйкес болады. Оларға тетраэдр (23 қарапайым классы, тетраэдрдың
симметрия осьтері), куб және октаэдр (432 аксиал классы, октаэдр немесе
кубтың симметрия осьтері) жатады. Қалған кластарды жоғарыда
көрсетілгендей кезегімен симметрия центрін немесе симметрия
жазықтықтарын қосып шығаруға болады. Реті 2-ші осьті қосуға
болмайды, өйткені осьтердің барлық мүмкін терулері таусылған.
26.
Қатты дене физикасы мен материалтану кафедрасыКристаллографияда грек сөздері қолданылады: моно – бір; ди – екі;
тетра – төрт; пента – бес; гекса – алты; окта – сегіз, дека – он; додека –
он екі; эдра – қабырға; гониа – бұрыш; клино – ылди; пинакс – тақта;
скалена – қисық, түзу емес; трапеца – төртбұрыштық; теми – жарты;
энантио – қарама-қарсы, кері; морфо – пішін, бейне, түрі, син –
ұқсастық.
27.
Қатты дене физикасы мен материалтану кафедрасыКристаллографиялық категориялар, жүйелер және сингониялар
Кристалдар ерекше бағыттардың санына және симметрия осьтеріне
байланысты үш категорияға бөлінеді :
жоғарғы категория – ерекше бағыттары жоқ, реті 2-шіден жоғары
бірнеше симметрия осьтері бар (мысалы – куб);
орта категория – реті 2-ден жоғары б.а. реті 3, 4 немесе
6 жалғыз симметрия осіне сәйкес бір ерекше бағыт
(мысалы – үш-, төрт- және алтықырлы призма);
төменгі категория – бірнеше ерекше бағыт, реті 2ден жоғары осьтер жоқ (мысалы – реті 2-ші үш осі
бар кірпіш).
28.
Қатты дене физикасы мен материалтану кафедрасыЖоғарғы категорияға реті 2-ден жоғары бірнеше симметрия
осьтері бар кристалдар жатады; атап айтқанда міндетті түрде реті
3-ші төрт ось және сонымен қатар реті 4 немесе 4 үш ось болуы
мүмкін.
Ол симметриясы жоғары кристалдар болады. Жоғарғы категория
кристаллында кез келген бағытқа басқа симметриялы эквиваленттік
бағыттар сай болады. Эквиваленттік бағыттарда кристалдың
қасиеттері бірдей болуы керек, сондықтан жоғарғы категория
кристалдарында қасиеттердің анизотропиясы аз байқалады.
Кристалдың физикалық қасиеттері: жылуөткізгіштік, диэлектрлік
өтімділік, электрөткізгіштік және т.б. бұл кристалдарда изотроптық
болады.
29.
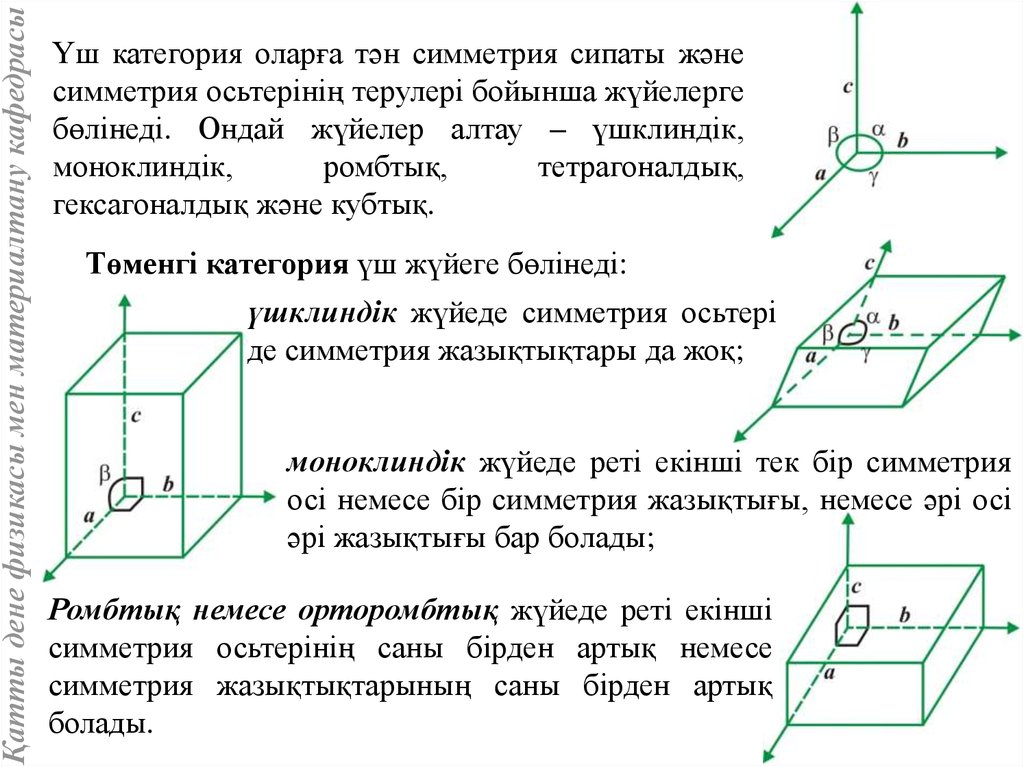
Қатты дене физикасы мен материалтану кафедрасыҮш категория оларға тән симметрия сипаты және
симметрия осьтерінің терулері бойынша жүйелерге
бөлінеді. Ондай жүйелер алтау – үшклиндік,
моноклиндік,
ромбтық,
тетрагоналдық,
гексагоналдық және кубтық.
Төменгі категория үш жүйеге бөлінеді:
үшклиндік жүйеде симметрия осьтері
де симметрия жазықтықтары да жоқ;
моноклиндік жүйеде реті екінші тек бір симметрия
осі немесе бір симметрия жазықтығы, немесе әрі осі
әрі жазықтығы бар болады;
Ромбтық немесе орторомбтық жүйеде реті екінші
симметрия осьтерінің саны бірден артық немесе
симметрия жазықтықтарының саны бірден артық
болады.
30.
Қатты дене физикасы мен материалтану кафедрасыОрта категория үш жүйеге бөлінеді:
Тетрагоналдық жүйеде негізгі симметрия осінің
–
реті 4 немесе 4;
гексагоналдық жүйеде негізгі бір симметрия осінің реті
–
6 немесе 6;
Кристалдардың сыртқы пішінін және олардың құрылысын зерттейтін
кристаллографтар гексагоналдық жүйеден реті 3-ші жоғарғы осі бар
тригоналдық кристалдарды бөлек қарастырады.
Тригоналдық немесе ромбоэдрлық жүйеде негізгі бір
–
симметрия осінің реті 3 немесе 3;
31.
Қатты дене физикасы мен материалтану кафедрасыЖоғарғы категорияға реті үшінші төрт симметрия
осьтері бар жалғыз кубтық жүйе жатады.
Алты жүйеге бөлудің орнына жеті сингонияға бөлуге
болады, жүйелер мен сингониялардың аталуы бірдей
(тригоналдық сингония қосылады).
Нүктелік топтың халықаралық символын жазу ережелері
Сингония
Позициялары
I
II
III
Үшклиндық
Кристалдың кез келген бағытына сай бір символ
Моноклиндық
Реті 2 ось немесе Y осі бойымен m жазықтыққа нормаль (бірінші
орнықтыру) немесе Z осі бойымен (екінші орнықтыру)
Ромбтық
Реті 2 ось немесе m жазықтыққа нормаль координаттық ось бойымен:
X осі
Тригоналдық
Тетрагоналдық
Гексагоналдық
Реті жоғарғы ось
(ерекше бағытқа сай)
Кубтық
Координаттық жазықтықтар немесе осьтер
Y осі
Z осі
Реті 2 ось немесе m бағыт бойымен:
Координаттық
бағыттар
Диагоналдық
бағыттар
3
Диагоналдық жазықтықтар немесе осьтер
32.
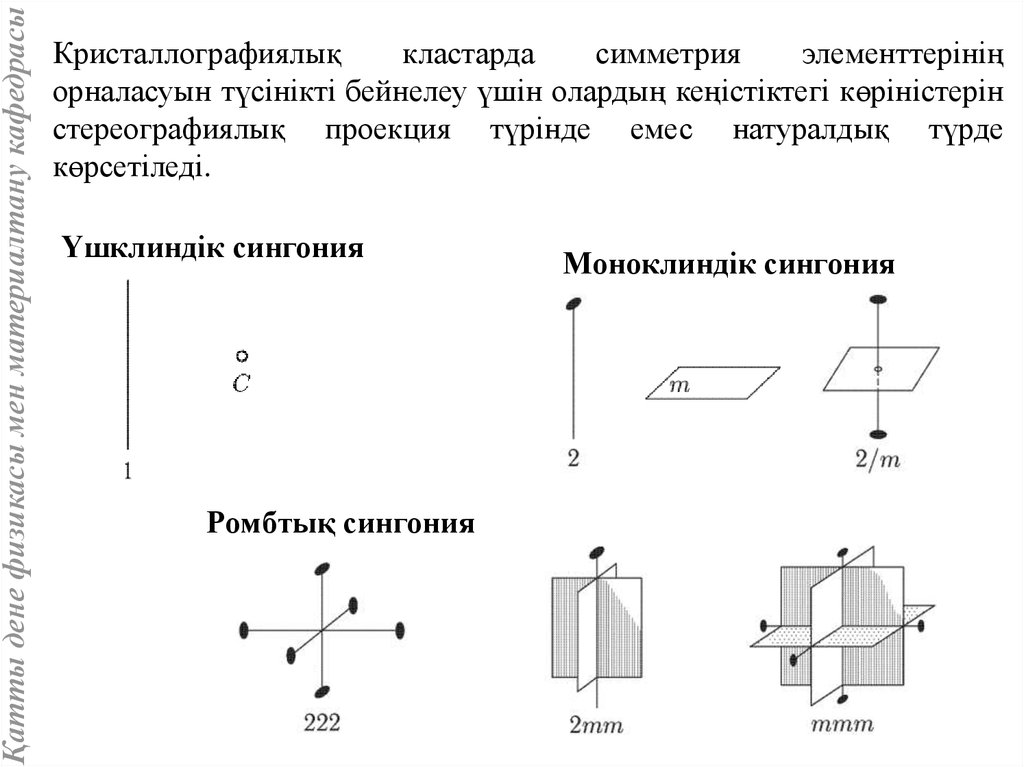
Қатты дене физикасы мен материалтану кафедрасыКристаллографиялық
кластарда
симметрия
элементтерінің
орналасуын түсінікті бейнелеу үшін олардың кеңістіктегі көріністерін
стереографиялық проекция түрінде емес натуралдық түрде
көрсетіледі.
Үшклиндік сингония
Ромбтық сингония
Моноклиндік сингония
33.
Қатты дене физикасы мен материалтану кафедрасыТетрагоналдық сингония
34.
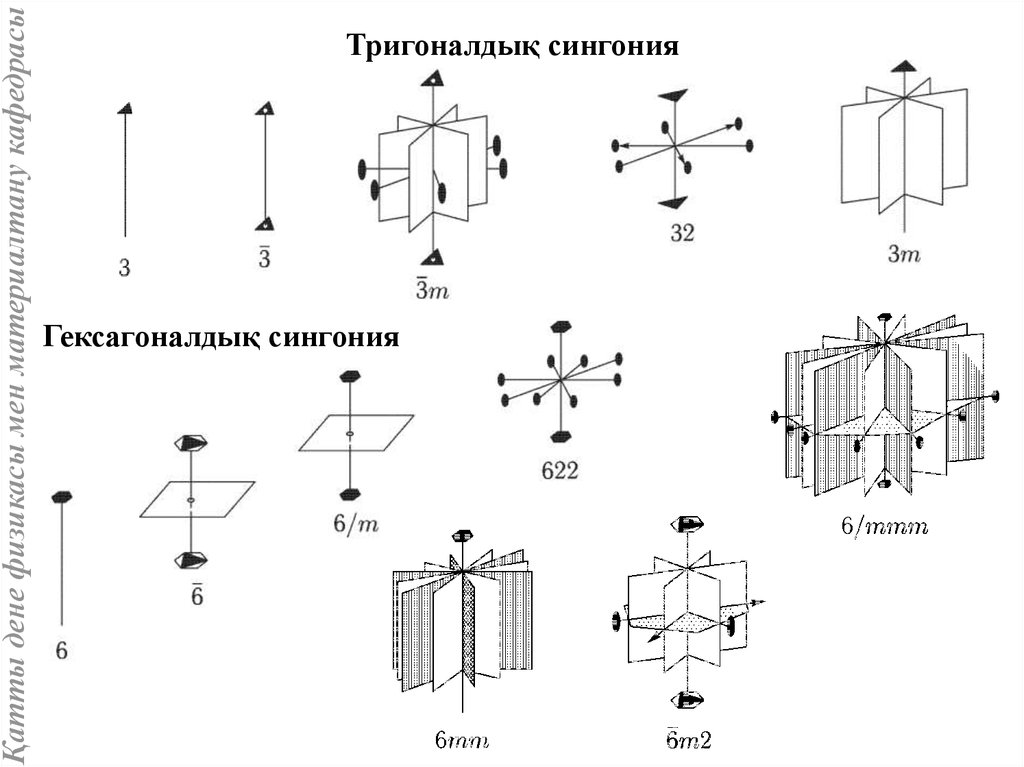
Қатты дене физикасы мен материалтану кафедрасыТригоналдық сингония
Гексагоналдық сингония
35.
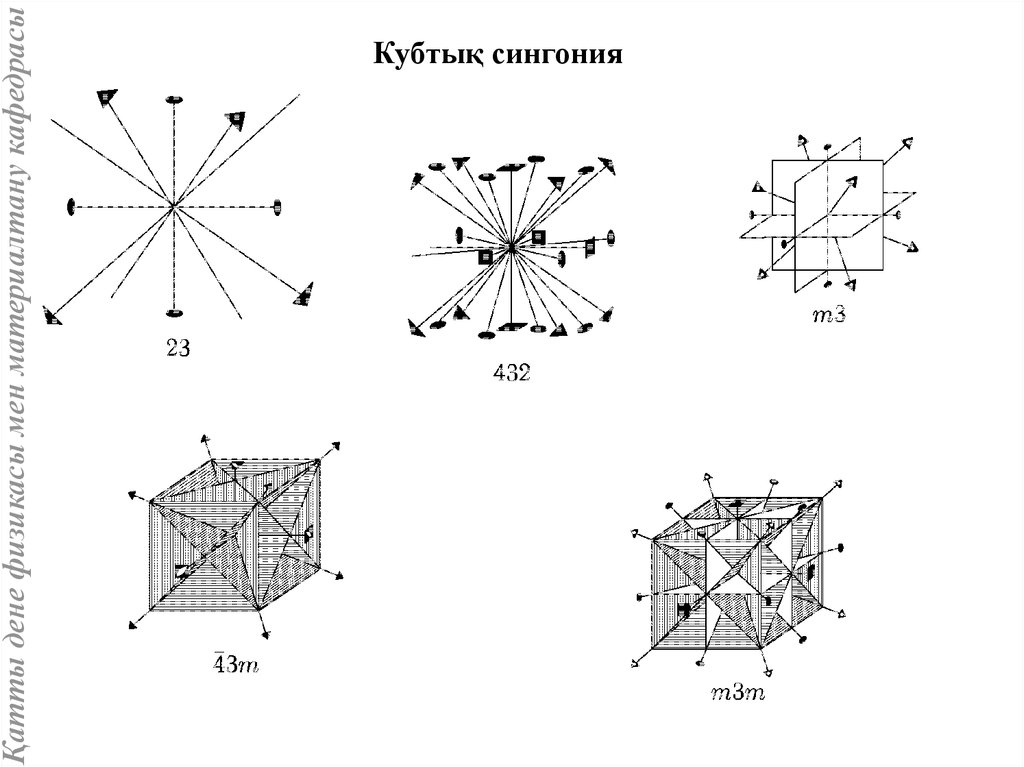
Қатты дене физикасы мен материалтану кафедрасыКубтық сингония
36.
Қатты дене физикасы мен материалтану кафедрасыКристаллографиялық номенклатура
Шенфлис номенклатурасы ең аз хабар береді, бірақ оны физик-теоретиктер жақсы
көреді. Ол келесі жолмен тұрғызылған:
тек симметрия осьтері бар топтар Сn деп белгіленеді, бұл жерде n – осьтің реті;
симметрия осьтері және оларға параллель симметрия жазықтықтары бар топтар Cnv
деп белгіленеді (v – вертикал символы);
симметрия осьтері және оларға перпендикуляр симметрия жазықтықтары бар топтар
Cnh деп белгіленеді (h – горизонтал символы);
симметрия осьтері және перпендикуляр 2 осі бар топтар Dn деп белгіленеді;
егер топта симметрия осьтері, осьтерге параллель n жазықтықтары және осьтерге
перпендикуляр жазықтық бар болса, онда осындай топтар Dnh деп белгіленеді;
тек инверсиялық симметрия осьтері бар топтар Sn деп белгіленеді;
үш өзара перпендикуляр 2 осьтері бар топ V = D2 деп белгіленеді;
егер топта үш 2 ось және үш симметрия жазықтықтары бар болса, онда осындай топ
Vh = D2h деп белгіленеді;
үш 2 осьтері және диагоналдық симметрия жазықтықтары бар топтар Vd = D2d деп
белгіленеді (d – диагональ символы);
тетраэдр топтары T, ал октаэдр топтары О деп белгіленеді через;
егер тетраэдрда диагоналдық жазықтықтар бар болса, онда осындай топ Td, ал егер
горизонтал жазықтықтар бар болса – онда Th деп белгіленеді;
октаэдр тобында да дәл сондай болады – Oh деп горизонтал симметрия жазықтықтары
бар топтар белгіленеді.
37.
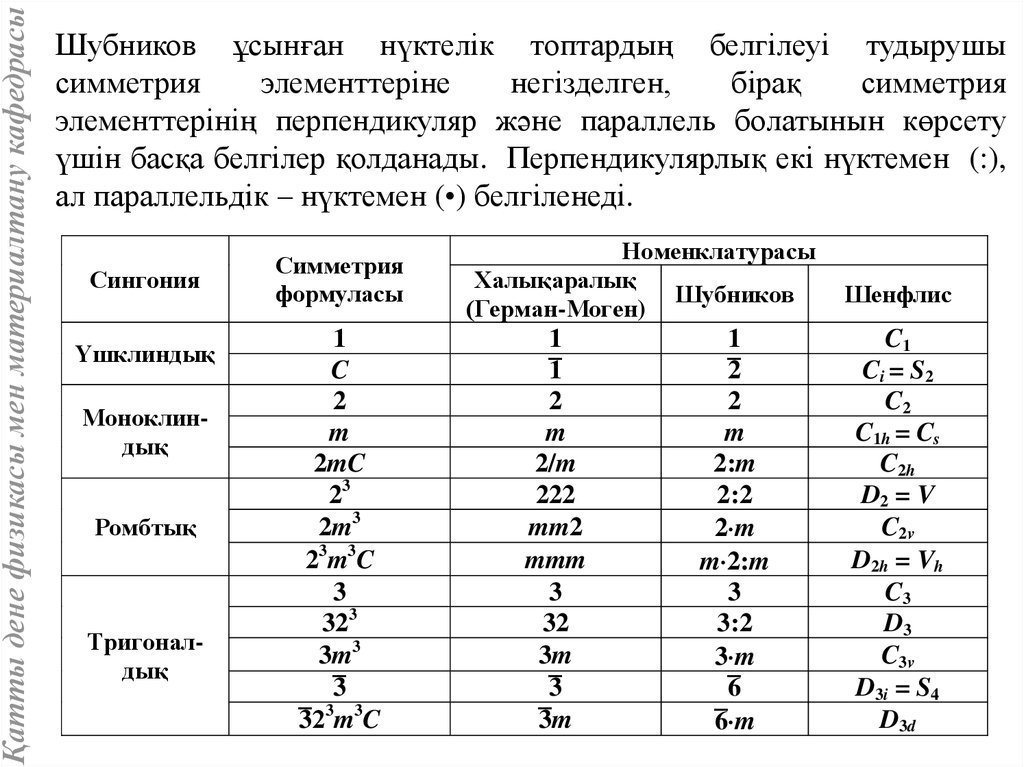
Қатты дене физикасы мен материалтану кафедрасыШубников ұсынған нүктелік топтардың белгілеуі тудырушы
симметрия
элементтеріне
негізделген,
бірақ
симметрия
элементтерінің перпендикуляр және параллель болатынын көрсету
үшін басқа белгілер қолданады. Перпендикулярлық екі нүктемен (:),
ал параллельдік – нүктемен (•) белгіленеді.
Сингония
Үшклиндық
Моноклиндық
Ромбтық
Тригоналдық
Симметрия
формуласы
1
C
2
m
2mC
23
2m3
23m3C
3
323
3m3
¯
3
3 3
¯2 m C
3
Номенклатурасы
Халықаралық
Шубников
(Герман-Моген)
1
¯
1
2
m
2/m
222
mm2
mmm
3
32
3m
¯
3
¯m
3
1
¯
2
2
m
2:m
2:2
2 m
m 2:m
3
3:2
3 m
¯
6
¯ m
6
Шенфлис
C1
Ci = S2
C2
C1h = Cs
C2h
D2 = V
C2v
D2h = Vh
C3
D3
C3v
D3i = S4
D3d
38.
Қатты дене физикасы мен материалтану кафедрасыСингония
Тетрагоналдық
Гексагоналдық
Кубтық
Симметрия
формуласы
4
424
4mC
4m4
424m5C
¯
4
¯22m2
4
6
3m(6
¯)
3 4
32 m
626
6mC
6m6
626m7C
2334
¯423m3C
3
¯334m6
4
433426
433
¯426m9C
Номенклатурасы
Халықаралық
Шубников
Шенфлис
(Герман-Моген)
4
4
C4
422
4:2
D4
4/m
4:m
C4h
4mm
C4v
4 m
4/mmm
D4h
m 4:m
¯
4
¯
4
S4
¯2m
4
D2d = Vd
¯ m
4
6
6
C6
¯
6
3:m
C3h
¯m2
6
D3h
m 3:m
622
6:2
D6
6/m
6:m
D6h
6mm
C6v
6 m
6/mmm
D6h
m 6:m
23
3/2
T
m3
¯/2
6
Th
¯3m
4
3/4
¯
Td
432
3/4
O
m3m
¯/4
6
Oh
39.
Қатты дене физикасы мен материалтану кафедрасы№2 тестілік тапсырманың үлгісі
1.
№
вариант
Жоғарғы категория кристалдарында неше ерекше бағыт
болады?
A) 1
B) 2
C) 3
D) 4
E) 0
2.
Моноклиндық сингонияда:
A) а ≠ b ≠ с, α = γ = 90° ≠ β
B) а = b ≠ с, α ≠ γ ≠ β ≠ 90°
C) а ≠ b ≠ с, α = γ = β = 90°
D) а ≠ b = с, α = γ = 90° ≠ β
E) а ≠ b ≠ с, α = γ = β ≠ 90°
3.
Гексагонал сингонияда:
A) а ≠ b ≠ с, α = γ = 90° ≠ β
B) а = b ≠ с, α ≠ γ ≠ β ≠ 90°
C) а ≠ b ≠ с, α ≠ β ≠ γ ≠ 90°
D) а ≠ b = с, α = γ = 90° ≠ β
E) а = b ≠ с, α = β = 90° ≠ γ = 120°
4.
Бағыт символы келесі түрде жазылады:
A) [[uvw]]
B) [uvw]
C) {uvw}
D) <uvw>
E) (uvw)
5.
mmm нүклелік тобының кристаллы қандай сингонияға
жатады :
A) Ромбтық
B) Тригоналдық
C) Гексагоналдық
D) Тетрагоналдық
E) Кубтық
____________________ (Аты-жөні) №_____ тобы
Бағыттаушы косинустар матрицасынан симметрия
осінің ретін және оның орналасуын анықта:
1 0 0
A) Х1 осі бойынша реті 2-ші ось
6. B) Х2 осі бойынша реті 2-ші ось
0 0 1
0 1 0
C) Х3 осі бойынша реті 2-ші ось
D) Х1 осі бойынша реті 4-ші ось
E) Х2 осі бойынша реті 4-ші ось
Симметрия элементтерінің стереографиялық
проекциясы суретте көрсетілген кристалл қандай
сингонияға жатады:
A) Ромбтық
7.
B) Тригоналдық
C) Гексагоналдық
D) Тетрагоналдық
E) Кубтық
Симметрия элементтерінің стереографиялық
проекциясы суретте көрсетілген кристалл үшін
нүктелік симметрия тобын жаз:
A) 4mm
8.
B) 4/mmm
C) 422
D) 432
E) 224
Бағыттаушы косинустар матрицасынан симметрия
осінің ретін және оның орналасуын анықта:
0 0 1
A) Х1 осі бойынша реті 2-ші ось
9. B) Х2 осі бойынша реті 2-ші ось
0 1 0
1 0 0
C) Х3 осі бойынша реті 2-ші ось
D) Х1 осі бойынша реті 4-ші ось
E) Х2 осі бойынша реті 4-ші ось
Симметрия жазықтығынан шағылудың бағыттаушы косинустар
матрицасының анықтауышы неге тең?
A) -1
10. B) -½
C) 0
D) ½
E) 1
40.
Қатты дене физикасы мен материалтану кафедрасы№2 бақылау жұмысының үлгісі
Вариант
1
(2 балл)
2
(2 балл)
3
(2 балл)
4 3m нүктелік симметрия тобы үшін симметрия элементтерінің стереографиялық
проекциясын бейнеле. Бұл симметрия классы қандай шекті топқа жатады?
4
(2 балл)
Келесі теореманы (графикалық және аналитикалық түрде) дәлелде: Жұп (4) симметрия
осінің оған перпендикуляр симметрия жазықтығымен қиылысуы симметрия центрі
болады.
m3m класының кристаллында {112} жазықтықтарын бейнеле.
6/m симметрия элементтерінің біріккен әрекетінің матрицасын анықта.
5
(2 балл)
Cимметрия элементтерінің толық жинағын шығар
= 45 .
3-4 дәріске қосымша әдебиет
Чупрунов Е.В., Хохлов А.Ф., Фадеев М.А. Основы кристаллографии: учебник
для вузов. – М.: Издательство Физико-математической литературы, 2004. - 500 с.
Попов Г.М., Шафрановский И.И. Кристаллография: учебник для студентов
геологических специальностей вузов. – М.: Высшая школа, 1972. - 352 с.




























 Физика
Физика








