Дисперсионный анализ

1. Дисперсионный анализ

Задача дисперсионного анализа:
сравнить две или более выборочные дисперсии и оценить
существенность различий между средними значениями
результативного признака в группах.
Используемые критерии:
2 группы – критерий Стьюдента (t-критерий)
Более 2 групп – критерий Фишера (F-критерий)
1

2. Однофакторный дисперсионный анализ

Пусть на некоторый признак Y воздействует фактор X,
который имеет m постоянных уровней (градаций). Число
наблюдений на каждом уровне n1, n2,…nm. Требуется
выяснить, оказывает ли существенное влияние фактор X на
изучаемую величину Y.

3. Обозначения:

yij – значение результативного признака j-го
элемента в i-й группе
i – номер группы
j – номер элемента, j=1, 2, …, ni
ni – численность i-й группы
yi – средняя величина результативного признака в i-й
группе
y – общая средняя результативного признака

4. Математическая модель

Наблюдаемое значение
yij i ij i ij
где yij – значение результативного признака в j-м испытании
при i-м уровне фактора
i – среднее значение результативного признака при i-м
уровне фактора
– общее среднее значение всей совокупности опытных
данных
i= i-
- величина, характеризующая влияние i-го уровня
фактора на общее среднее значение
ij=yij- i – ошибка
4

5. Математическая модель

Нулевая гипотеза H0: различия между уровнями фактора не
превосходят случайные различия (исследуемый фактор не
влияет на результативный признак), т.е. уровни фактора не
влияют на общее среднее значение результата
эксперимента
H 0 : 1 2 ... m
Альтернативная гипотеза H1: различия между уровнями
фактора достоверно превосходят случайные различия
(исследуемый фактор влияет на результативный признак).
5

6. Расчетные формулы

ni
yij
1) Групповая средняя
yi
j 1
ni
mi
2) Общая средняя
результативного признака
yi
y i 1
m
6

7. Расчетные формулы

3) Общая сумма квадратов отклонений наблюдаемых значений
от общей средней
m n
2
SSобщ yij y
i 1 j 1
4) Факторная сумма квадратов отклонений групповых средних
от общей средней (межгрупповая сумма квадратов)
m
SSфакт y i y ni
2
i 1
5) Остаточная сумма квадратов отклонений наблюдаемых значений
от своей групповой средней (внутригрупповая сумма квадратов)
m
ni
SS ост yij yi
2
i 1 j 1
7

8. Расчетные формулы

SS общ SSфакт SS ост
SSфакт
SSост
характеризует влияние фактора
характеризует воздействие случайных причин
Число степеней свободы:
m
f общ N 1, где N n i общее число наблюдений
i 1
fфакт m 1,где m число уровней ( градаций ) фактора
f ост N m
8

9. Дисперсии

7) Факторная
6) Общая
y
m
S
2
общ
n
i 1 j 1
ij
y
2
S 2факт
N 1
S
2
ост
y
ni
i 1 j 1
i 1
2
i
y ni
m 1
9) Критерий Фишера
8) Остаточная
m
y
m
ij
yi
N m
2
Fнабл
Если
2
S факт
2
S ост
Fнабл>Fкрит, то H0 отвергается.
9

10. Пример

Методом дисперсионного анализа определить
достоверность генетического влияния отцов на массу телят
при рождении. Принять уровень значимости =0,05.
Уровень
фактора
Результативный
признак yij - масса
телёнка, кг
Численность
группы,
ni
А
Б
40; 38; 43; 42
4
38; 32; 40; 34; 35
5
В
37; 30; 31; 32; 35
5
Выдвигаются гипотезы:
H0: телята от разных отцов не отличаются по массе при рождении.
H1: телята от разных отцов отличаются по массе при рождении
10

11. Решение задачи с помощью Пакета анализа MS Excel

1. Загрузить Пакет анализа MS Excel , выполнив действия:
Данные → Анализ → Анализ данных.
2. Ввести данные в ячейки A1:F4, как показано на рис. 1.
Рис. 1.
3. Выбрать инструмент «Однофакторный
дисперсионный анализ». Нажать кнопку ОК.
11

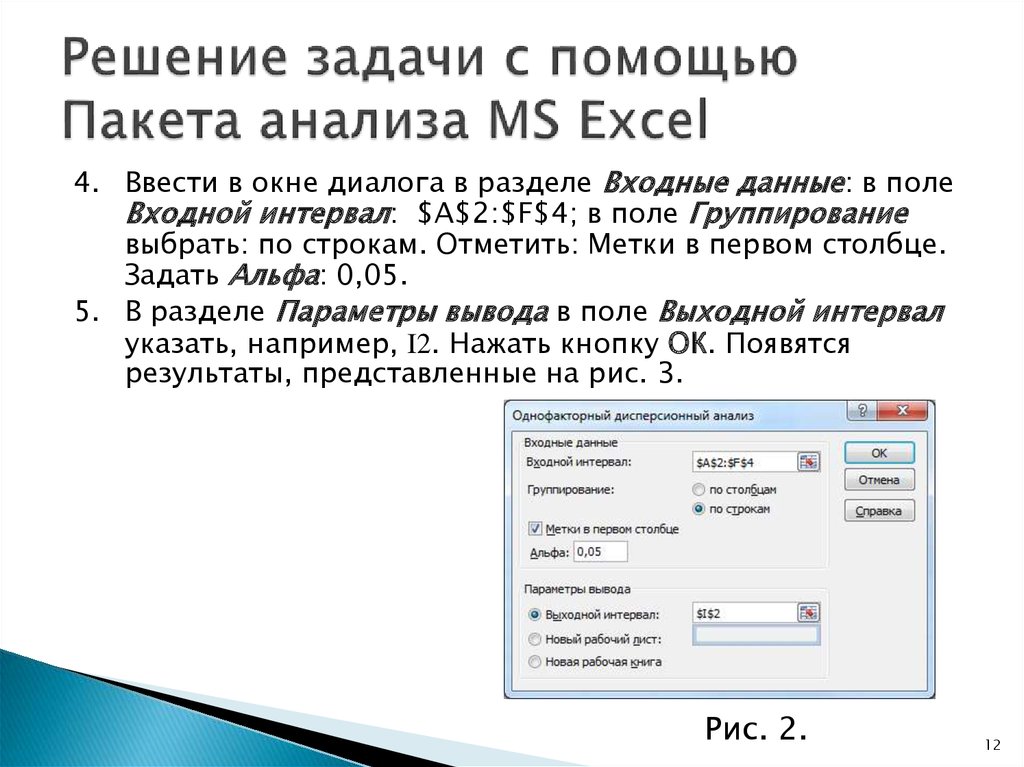
12. Решение задачи с помощью Пакета анализа MS Excel

4. Ввести в окне диалога в разделе Входные данные: в поле
Входной интервал: $A$2:$F$4; в поле Группирование
выбрать: по строкам. Отметить: Метки в первом столбце.
Задать Альфа: 0,05.
5. В разделе Параметры вывода в поле Выходной интервал
указать, например, I2. Нажать кнопку ОК. Появятся
результаты, представленные на рис. 3.
Рис. 2.
12

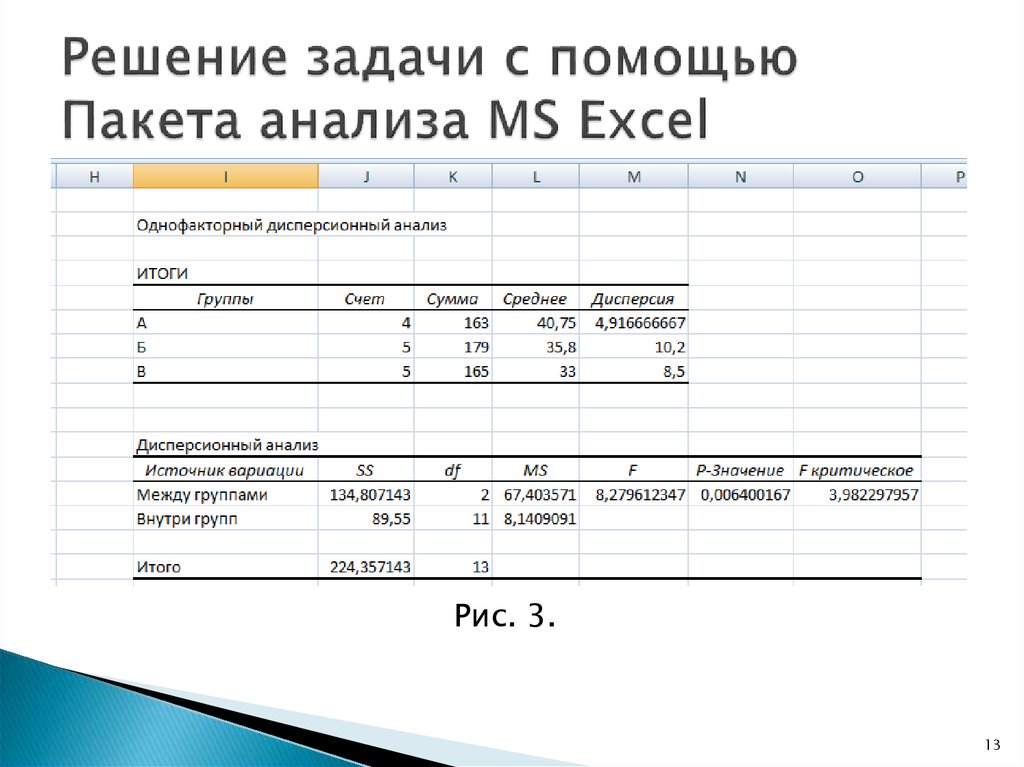
13. Решение задачи с помощью Пакета анализа MS Excel

Рис. 3.
13

14. Сравнение групповых средних дисперсионного комплекса

1) Метод Дж. Тьюки (1949 г.)
Область применения: проверка нулевой
гипотезы при сравнении групповых
средних x1 и x 2 равновеликих групп.
Критерий оценки:
tQ
x1 x 2
2
s ост
n
Если tQ Qкр ( , k=N-a), то нулевую гипотезу
отвергают (a – число градаций фактора).
14

15. Сравнение групповых средних дисперсионного комплекса

2) Метод Г. Шеффе (1953 г.)
Область применения: проверка нулевой гипотезы при
сравнении групповых средних и равновеликих и
неравновеликих групп.
Критерий оценки:
x x
F
F
1
2
2
sост
x1 x 2
2
sост
n
при n1 n 2
2
n1n 2
при n1 n 2
n1 n 2
Нулевую гипотезу отвергают, если
F
a 1 Fкр
,
где a – число градаций фактора, Fкр определяют по таблице
для принятого , k1=a-1, k2=N-a.
15

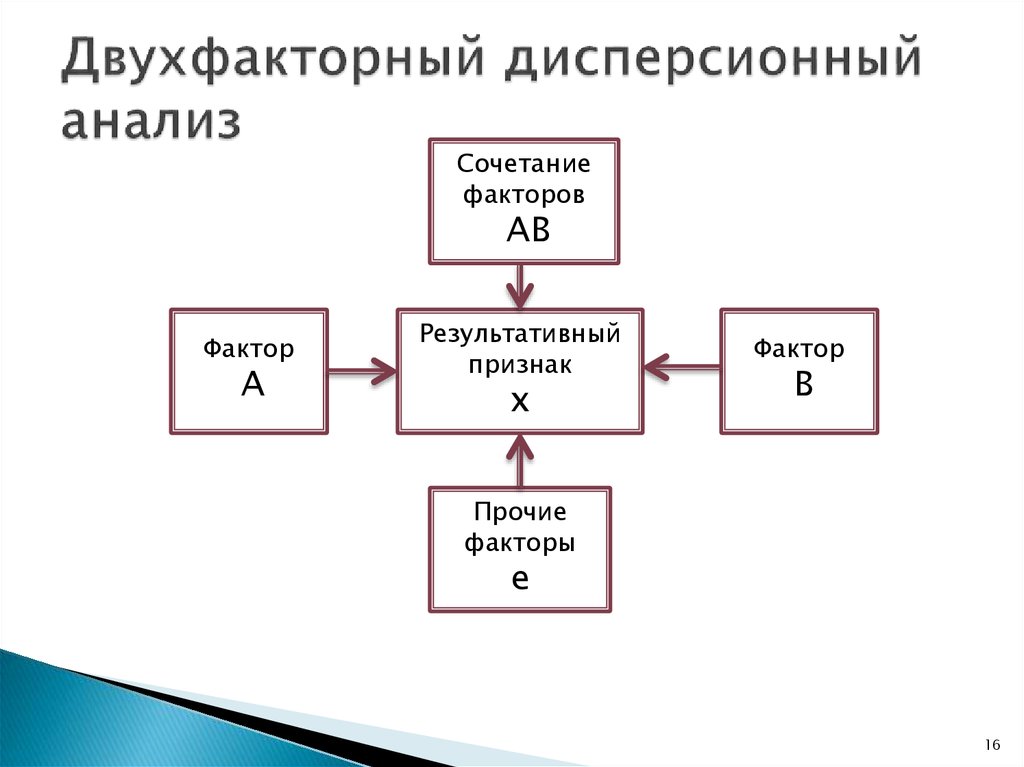
16. Двухфакторный дисперсионный анализ

Сочетание
факторов
AB
Фактор
A
Результативный
признак
x
Фактор
B
Прочие
факторы
e
16

17. Двухфакторный дисперсионный анализ

17

18. Двухфакторный дисперсионный анализ без повторений. Математическая модель

19. Оценки средних

20. Суммы квадратов отклонений

21. Формулы для расчёта дисперсий

22. Правило проверки гипотез

23. Пример 1

24. Двухфакторный дисперсионный анализ с повторениями. Математическая модель

25. Суммы квадратов отклонений

26. Оценка средних

27. Схема анализа и порядок вычисления сумм

28. Пример 2

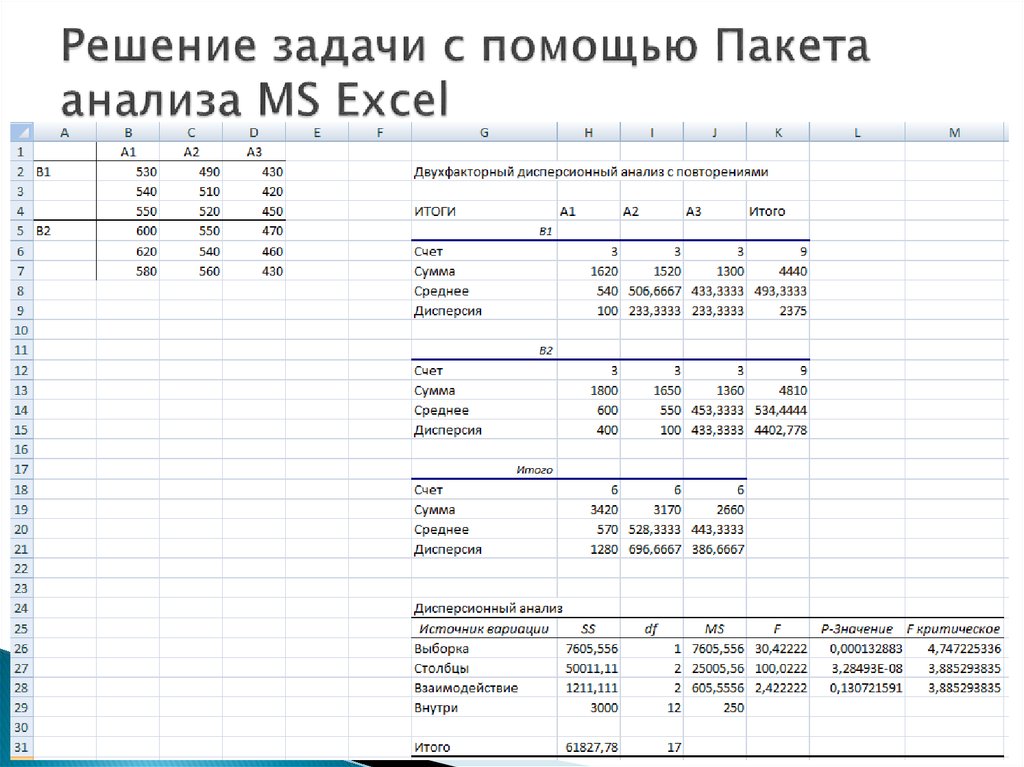
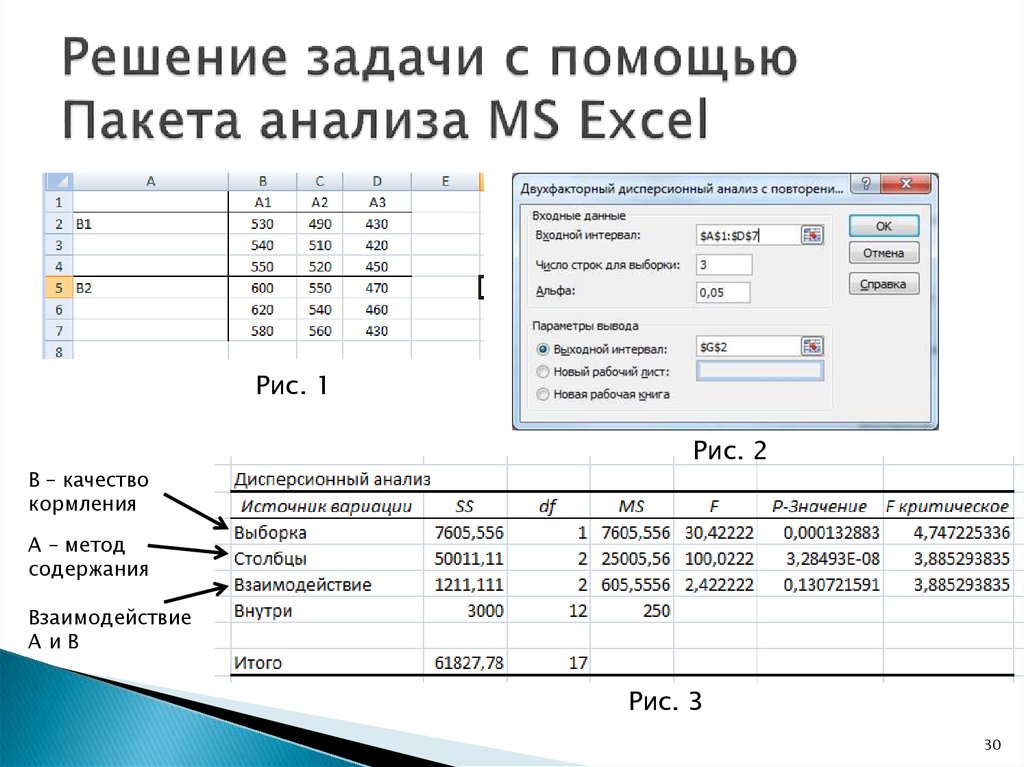
29

29. Решение задачи с помощью Пакета анализа MS Excel

Рис. 1
Рис. 2
B – качество
кормления
A – метод
содержания
Взаимодействие
AиB
Рис. 3
30

30. Решение задачи с помощью Пакета анализа MS Excel

Исследовать влияние качественного раствора A, который
варьируется на четырёх уровнях, на накопление
микроорганизмов.
Уровень
фактора
Результативный
признак
a1
a2
1,30; 1,50; 1,70; 1,90
a3
2,20; 2,00; 2,00; 2,10
a4
2,10; 1,70; 1,40; 1,80
2,70; 2,00; 2,20; 2,40
Численность группы n1=n2=n3=n4=4
31

31. Пример

Групповые средние:
1,60; 2,33; 2,08; 1,75
Общая средняя
1,94
Отклонения групповых средних от общей средней
-0,34; 0,39; 0,14; -0,19
Сумма
квадратов
Степень
свободы
Дисперсии
Fнабл
Fкр
Фактор A
1,272
3
0,424
6,83
3,48
Ошибка
0,745
12
0,062
Так как Fнабл>Fкрит, то влияние фактора признаётся
значимым.
32