Правила дифференцирования

1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ

Урок № 38
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
План урока
1 Повторяем
производную функции
2 Новый материал
(3 теоремы)
3 Решение задач
4 Запись ДЗ
Функции, как и живые существа,
характеризуются своими
особенностями.
П. Монтель

2.

Правила дифференцирования
U V
C U
U V
U V
С U
U V U V
U V U V
U
2
V
V
f ( g ( x)
U
f (U ) g ( x)

3.

Формулы дифференцирования
x n x
n
e e x
x
ln x
1
х
С 0
n 1
x 2
a a
x
x
1
ln a
log a x
1
tgx 2
cos x
х 1
x
sin x cos x
1
x ln a
cos x
1
сtgx sin 2 x
sin x

4.

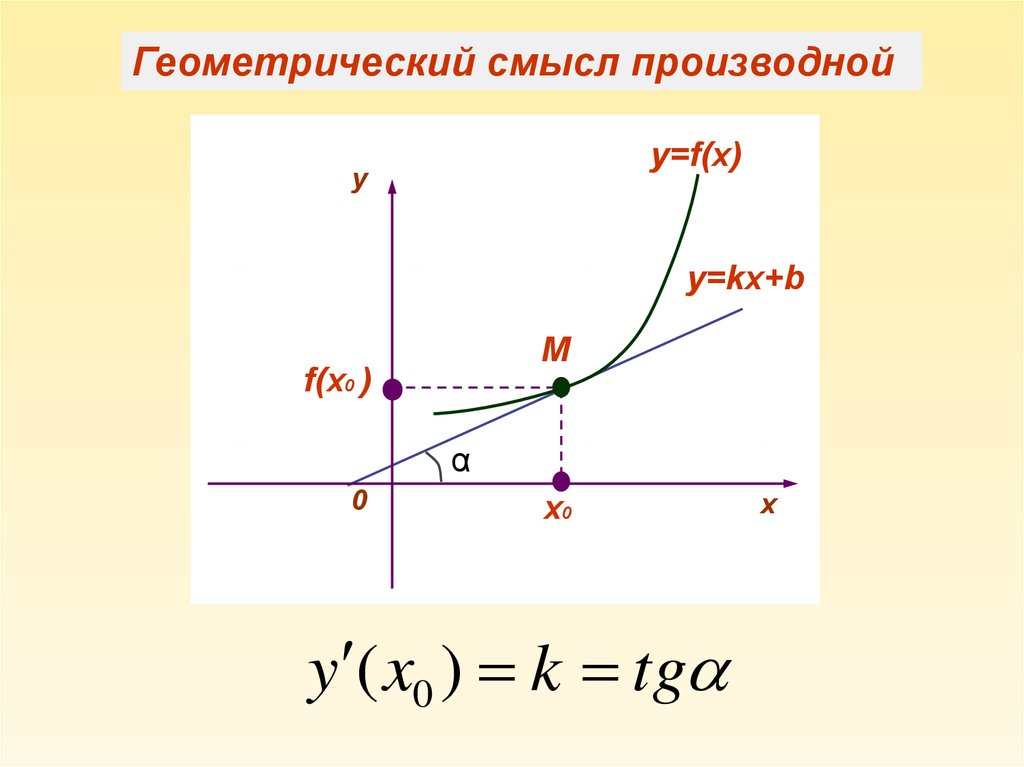
Геометрический смысл производной
y=f(x)
y
y=kx+b
М
f(x0 )
α
0
х0
y ( x0 ) k tg
х

5.

Возрастающие и убывающие функции
у
у
y=kx+b
y=kx+b
f(b)
f(a)
f(a)
f(b)
a
b
х
Функция возрастающая, если
a b
f (a) f (b)
a
b
х
Функция убывающая, если
a b
f (a ) f (b)

6.

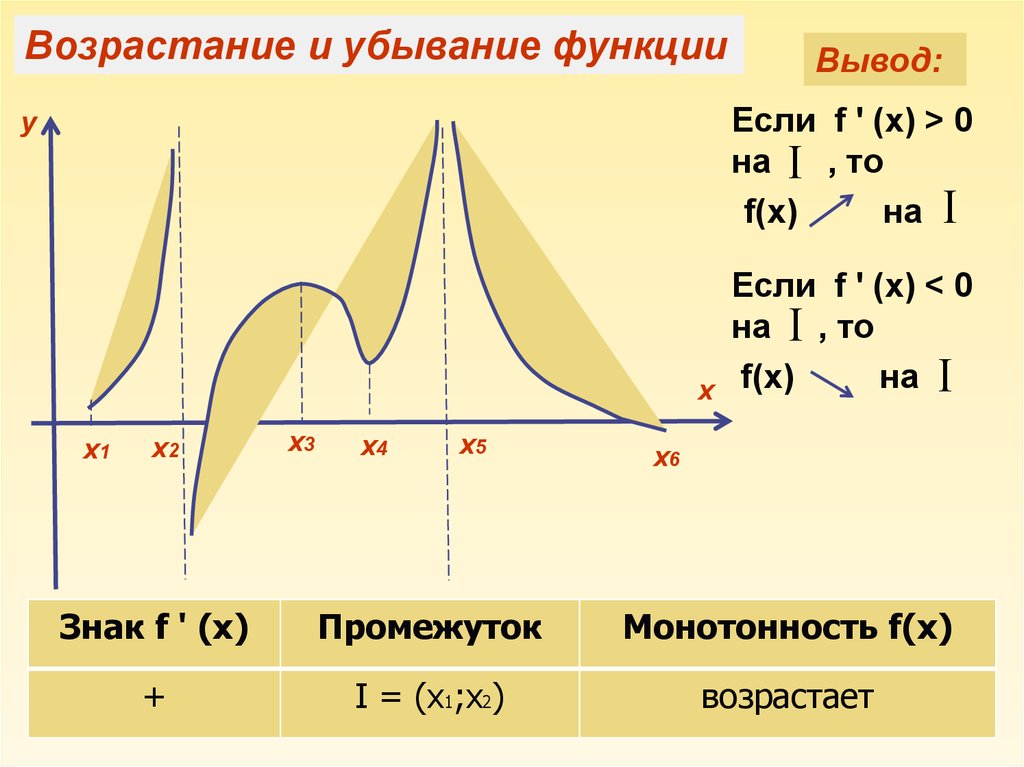
Возрастание и убывание функции
Вывод:
Если f ꞌ (x) > 0
на , то
f(x)
на
у
Если f ꞌ (x) < 0
на , то
на
х f(x)
х1
х2
х3
х4
х5
х6
Знак f ꞌ (x)
Промежуток
Монотонность f(x)
+
I = (x1;x2)
возрастает

7.

Теорема Лагранжа
Теорема 1:
Если функция y=f(x) непрерывна на [a;b] и
дифференцируема на (a;b),
то существует с Є (a;b) такое, что
f(b)-f(a)=f ꞌ(c)(b-a)
y
B
f(b)
f(a)
f (b) f (a )
k
b a
A
y=f(x)
a
с
b
x
f (b) f (a )
f (c)
b a

8.

Достаточное условие возрастания функции
Теорема 2:
Если функция y=f(x) дифференцируема на (a;b),
и f ꞌ(x)>0 для всех х Є (a;b),
то функция y=f(x) возрастает на (a;b).
Достаточное условие убывания функции
Теорема 3:
Если функция y=f(x) дифференцируема на (a;b),
и f ꞌ(x)<0 для всех х Є (a;b),
то функция y=f(x) убывает на (a;b).
Дано:
Доказать:
Доказательство:

9.

№ 900(1,3,5,7),902(1,3),903(1,3),904(1),905(1)

10.

Домашнее задание с урока 38
Учебник Алгебра 10-11 кл.
§ 49, с. 261-264,
№ 900(2,4,6,8), 902(2,4),
903(2,4), 904(2), 905(2)