Похожие презентации:
Дифференцирование функции одной переменной
1. Тема: Дифференциальное исчисление функции одной переменной
2. Производная функции
Определение. Производной функции y = f (x) вточке
x называется
предел
отношения
приращения
функции
Δy=f(x+Δx)–f(x)
к
приращению аргумента Δx при Δx 0, если этот
предел существует и конечен
f x x f x
y
f x lim
lim
x 0 x
x 0
x
Для
обозначения
используют символы:
производной
функции
dy df ( x )
y , f ( x ), ,
.
dx dx
3. Связь дифференцируемости и непрерывности функции
Если функция дифференцируема вданной точке, то она непрерывна в ней.
Обратное утверждение неверно, т. е.,
если функция непрерывна в точке, то она
может быть не дифференцируемой в этой
точке.
Например, функция y x непрерывна,
но не дифференцируема в точке x = 0.
4.
Техника дифференцированияПусть f (x) и g (x) дифференцируемые функции и с
константа, тогда справедливы соотношения
1. [c f (x)] = c f (x) .
2. [ f (x) g (x) ] = f (x) g (x) .
3. [ f (x) g (x) ] = f (x) g (x) + f (x) g (x) .
f ( x)
f ( x) g ( x) f ( x) g ( x)
4.
g 2 ( x)
g ( x)
.
5.
Теорема. (Производная сложной функции)Пусть
функция g (x) имеет производную в точке x0, функция f (g)
имеет производную в точке g0 = g (x0) . Тогда функция f(g(x))
будет иметь производную в точке x0 и справедливо
соотношение f ( g ( x)) f ( g ( x)) g ( x) .
Теорема. (Производная обратной функции) Пусть
y = f -1(x) обратная функция к функции x = f (y), имеющей
производную в точке y0, причем f (y0) 0. Тогда обратная
функция y = f -1(x) имеет производную в точке x0 = f (y0) ,
1
причем f 1 ( x 0 ) 1
или f 1 ( x 0 )
.
f ( y 0 )
f ( f 1 ( x0 ))
6. Таблица производных
1.u
u 1u ', const
2. 1
1
2 u
u
u
4. u
u
e e u
3.
5.
7.
8. sin u
cos u u
9.
6.
1
ln u u
u
u
a
u
1
2 u
u
a u ln a u
1
u
loga u
u ln a
arcsin u
1
1 u2
u
7.
10.cos u
12.
sin u u
1
u
tg u
2
cos u
14.
1
ctg u 2 u
sin u
11.
arccos u
13.
arctg u
15.
arcctg u
1
1 u2
u
1
u
2
1 u
1
u
1 u2
8. Пример
Найти производные первого порядкафункций
1
y 2x 3 x 2 4
2x
3
Решение. Применим формулу производной
суммы
1 2
3
y 2 x 3 x x
4
2
Далее используем формулы:
9.
22
( x ) 3 x ( x )' 3 x
3
x
1
2 x
( x )'
1
2 x
2 1
3
( x ) 2 x
( x )' 2 x
2
(4)' 0
Тогда:
1
3
y' 2 3x 3
2 x 0
2 x 2
2
1
1
6x
3.
2 x x
2
3
10.
y 2 cos x;x
Решение.
Используем
правило
дифференцирования произведения
uv u v uv
y 2 cos x 2
x
x
cos x 2 cos x
x
Далее, по таблице производных имеем:
x
Формула (5): 2 2 x ln 2
Формула (10): cos x sin x
11.
y 2 cos x 2x
x
cos x 2 cos x
x
2 x ln 2cos x 2 x sin x 2 x ln 2cos x sin x .
12.
Производная сложной функции. Вычислитьпроизводную y sin7 x;
Решение. Используем формулу
sin u
В данном случае
cos u u
u 7 x Тогда:
y (sin7 x ) cos7 x (7 x )
cos7 x 7 ( x ) 7cos7 x
13.
Теорема. (Производная функции, заданной параметрически)Если функция аргумента x задана параметрически:
x (t )
, t ,
y (t )
где (t) и (t) – дифференцируемы, причем (t) 0 , то
производная этой функции по переменной x вычисляется по
формуле
t
y x
, x= (t).
t
14.
Пусть функция у = f (x) задана уравнением F (x, y) = 0, неразрешенным относительно y. В этом случае говорят, что
функция y задана неявно.
Пусть уравнение F (x, y) = 0 задает y как неявную
функцию от x, т. е. y = f (x). Предположим, что функция y
дифференцируема. Если в уравнении F (x, y) = 0 под y
подразумевать функцию y (x), то это уравнение обращается в
тождество по аргументу x: F (x, y (x)) = 0.
Для
нахождения
производной
y (x)
нужно
продифференцировать по x обе части, помня, что y есть
функция от x, и затем разрешить полученное новое уравнение
относительно искомой производной. Как правило, она будет
зависеть от x и y: y (x) = (x, y).
15. Дифференциал функции
Пусть функция y f x имеет в точке xy
производную lim
f ( x ) 0
x 0 x
Тогда y f ( x ) x ( x ) x ,
где ( x ) 0 при x 0
16.
Причем, y f ( x ) x ( x ) x .Слагаемое f ( x ) x - главная часть
приращения функции.
17.
Определение. Дифференциалом функции y f xв точке x называется главная часть приращения
функции, равная произведению производной
функции
на
приращение
аргумента,
и
обозначается : dy f x x
Так
как
дифференциал
независимой
переменной
x
равен
приращению
этой
переменной: dx x x x , то
dy f x dx
18.
19.
20.
Правило Лопиталя21.
22.
Монотонность и экстремум функций23.
24.
25.
26.
27.
Геометрический смысл производнойПроизводная от функции y f x в
точке x0 равна угловому коэффициенту
касательной к графику функции в точке с
абсциссой x0 :
y
k tg lim
f x
x 0 x
28. Уравнения касательной и нормали
Уравнение касательной можно найти,используя уравнение прямой, проходящей
через данную точку ( x0 ; f ( x0 )) в заданном
направлении k : y y0 k x x0
А так как k f ( x0 ) то
y f ( x0 ) f ( x0 )( x x0 )
уравнение касательной.
29. Уравнение нормали
Прямая перпендикулярная касательной вточке касания называется нормалью к
кривой.
Угловые коэффициенты касательной и
нормали
связаны
условием
перпендикулярности:
1
kN
kK
30.
Потому уравнение нормали в точке ( x0 ; f ( x0 ))имеет вид:
1
y f ( x0 )
( x x0 ).
f ( x0 )
Углом между кривыми называют угол между
касательными к кривым в точке их пересечения.
31.
Односторонние производныеОпределение. Если функция y = f (x)
определена в левосторонней (правосторонней)
окрестности точки x0 и существует
lim
x x0 0
f ( x) f ( x0 )
f ( x0 0) f ( x0 )
x x0
то он называется производной от функции в
точке x0 слева, а
f ( x) f ( x0 )
lim
f ( x0 0) f ( x 0 )
x x0 0
x x0
производной в той же точке справа.
32.
Теорема. (Необходимое и достаточное условиесуществования производной в точке)
Функция y = f (x) имеет производную в точке тогда
и только тогда когда в этой точке существуют и
равны между собой производные функции слева и
справа, причем
f ( x0 ) f ( x0 ) f ( x0 )
.
Теорема. (Связь между дифференцируемостью
функции в точке и ее непрерывностью в этой точке)
Если функция y = f (x) имеет производную в точке
x0 , то она в этой точке непрерывна.
33. Экономический смысл производной. Эластичность
Пустьфункция
u=u(t)
выражает
количество произведенной продукции u за
время t. Необходимо найти производительность труда в момент времени t 0 .
За период времени от t 0 до t 0 t
количество
произведенной продукции
изменится от u0 u( t0 ) до
u0 u u( t0 t )
34.
Средняя производительность труда заэтот период времени:
u
zS
t
Определение. Производительностью
труда в момент t 0 называется предельное
значение средней производительности за
период времени от t 0 до t0 t при t 0 :
u( t0 t ) u( t0 )
du
u '( t0 )
lim
dt t t0 t 0
t
35.
Определение. Эластичностью функцииy=f(x) в точке x называется предел
y / y
y x
x
E x ( y ) lim
lim
f ( x )
x 0 x / x
x 0 x
y
y
Эластичность функции показывает на сколько
процентов изменится зависимая переменная y,
если независимая переменная
x получит
приращение в 1%.
В анализе и прогнозах ценовой политики
применяется понятие эластичности спроса.
36.
Пусть D=D(p) – функция спроса (зависит отцены товара p). Тогда под эластичностью спроса
понимается процентное изменение спроса при
изменении цены товара на 1%.
Различают следующие виды спроса:
1. Если |E(D)|>1, то спрос считается эластичным;
2. Если |E(D)|=1, то спрос нейтрален;
3. Если |E(D)|<1, то спрос неэластичен;
4. Если
E(D)=0,
то
спрос
совершенно
неэластичен.








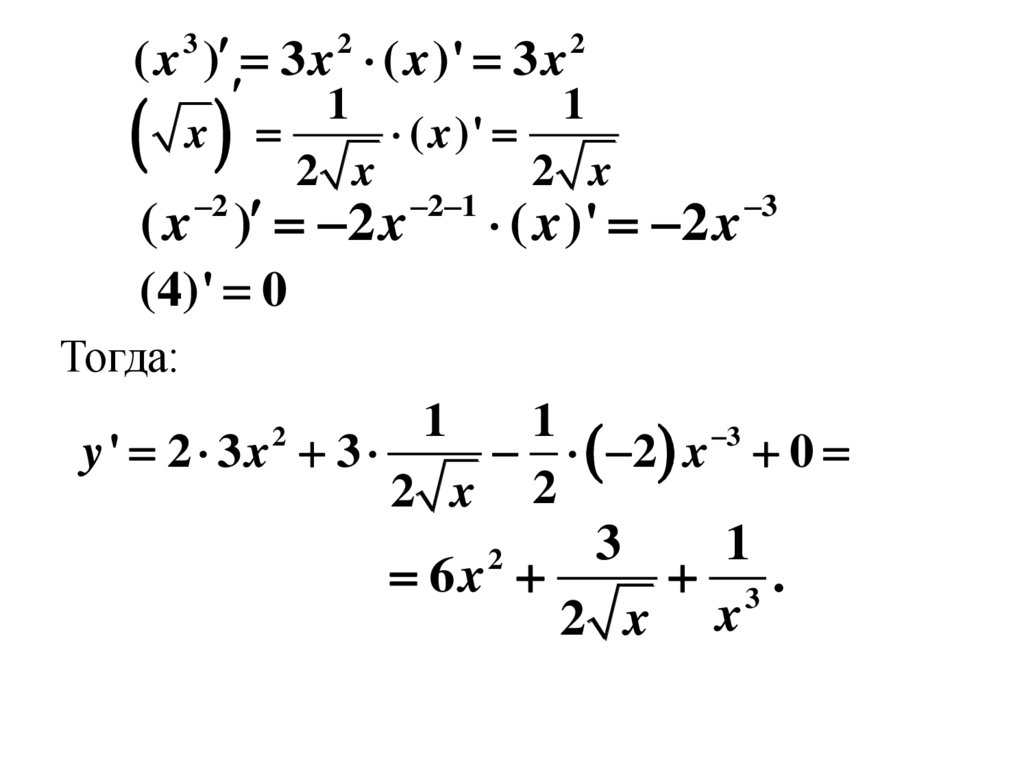

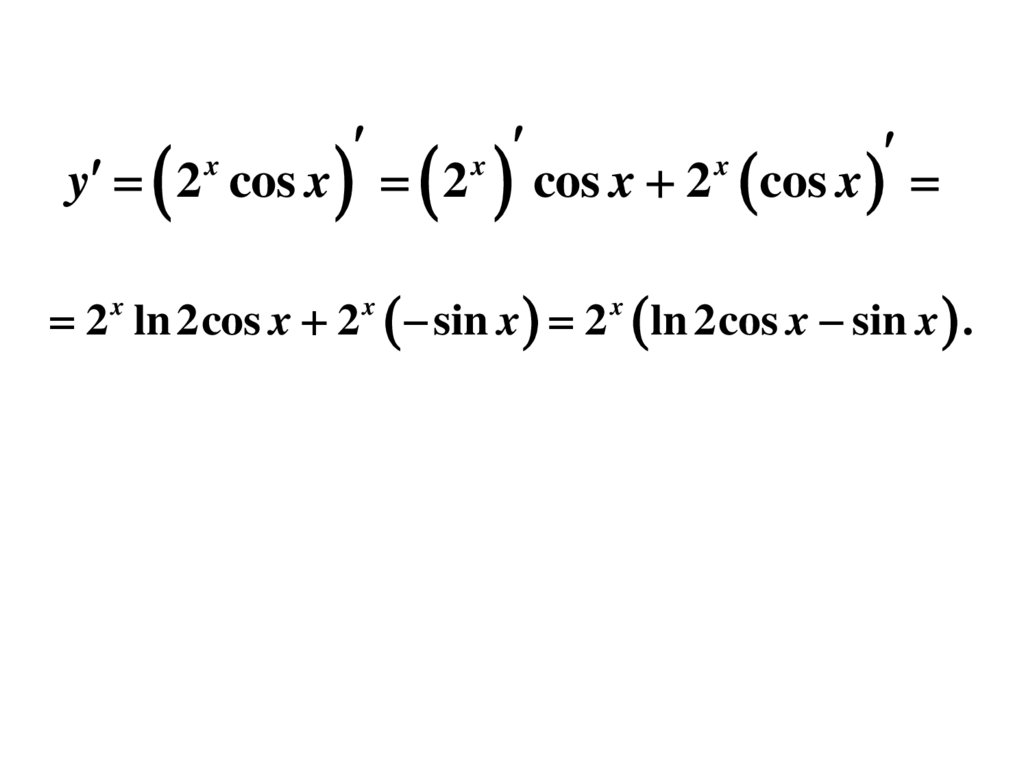


























 Математика
Математика








