Арккосинус и решение уравнения cos x = a

1. Арккосинус и решение уравнения cos x = a

Уроки № 1-2

2. Цели урока

ввести понятие arccos x;
вывести формулу решения уравнения
cos x=a, a 1 ;
рассмотреть уравнения на применение
этой формулы;
рассмотреть простейшие
тригонометрические неравенства.

3.

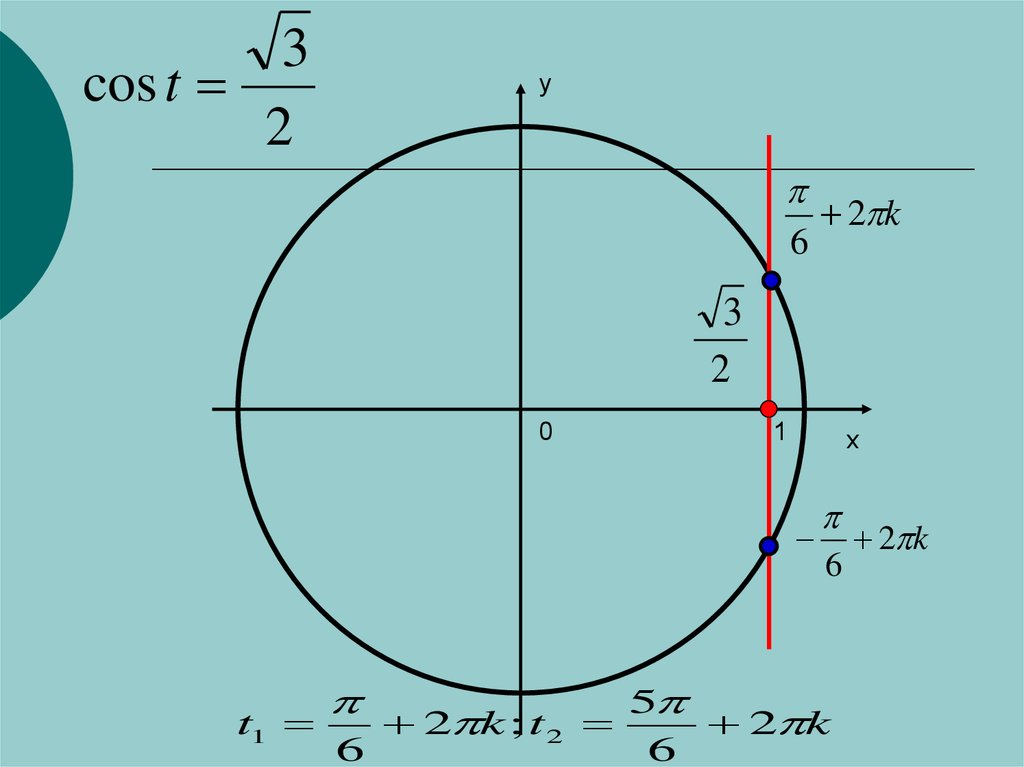
3
cos t
2
y
6
2 k
3
2
0
1
x
t1
6
2 k ; t 2
6
5
2 k
6
2 k

4.

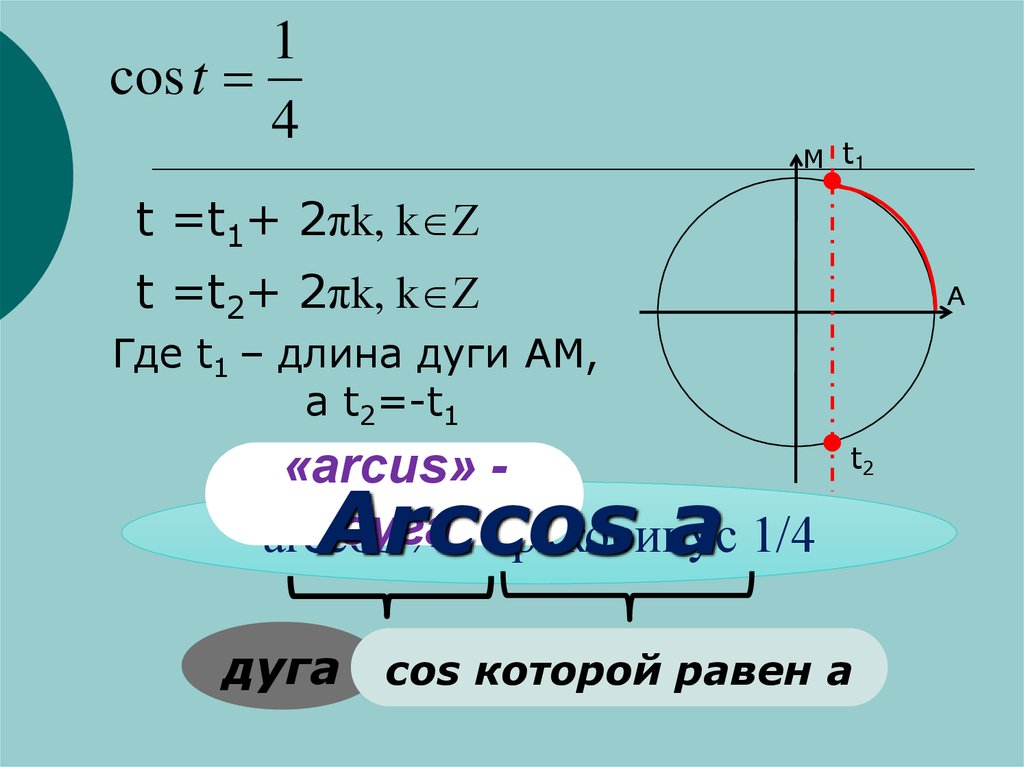
1
cos t
4
M t1
t =t1+ 2πk, k
t =t2+ 2πk, k
A
Где t1 – длина дуги АМ,
а t2=-t1
«arcus» дуга
arccos
¼ - арккосинус 1/4
Аrccos а
t2
дуга cos которой равен a

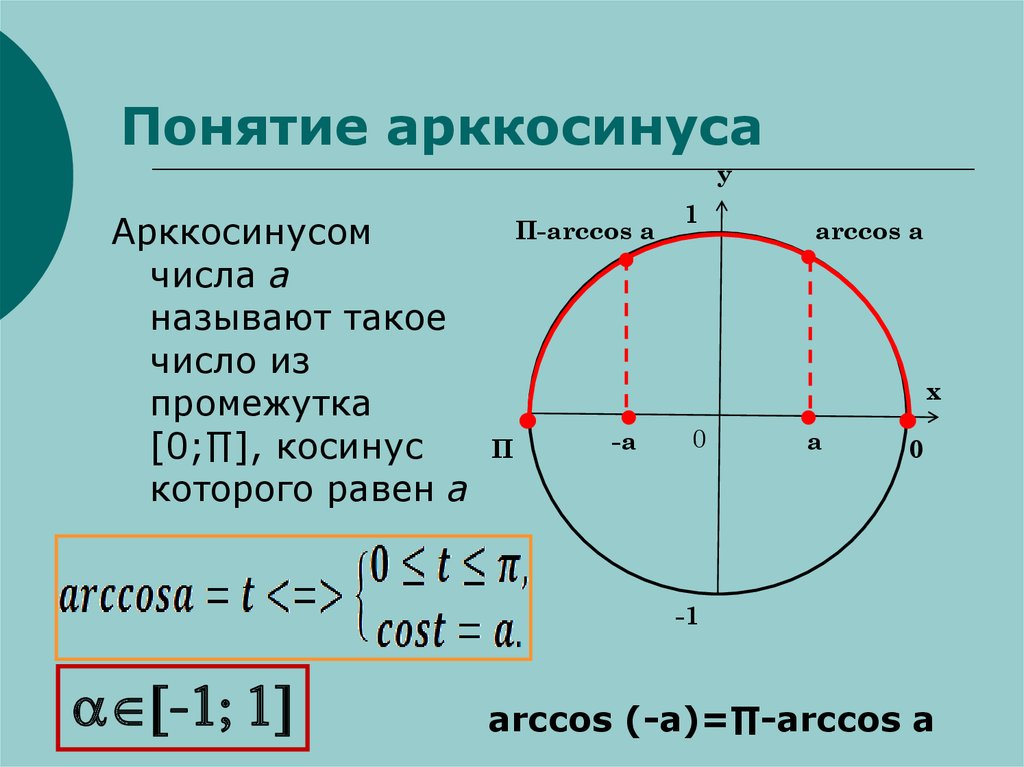
5. Понятие арккосинуса

у
Арккосинусом
числа а
называют такое
число из
промежутка
[0;∏], косинус
которого равен а
П-arccos a
1
arccos а
х
П
-а
0
а
0
-1
a -1; 1
arccos (-a)=∏-arccos a

6. Имеют смысл выражения?

3
3
arccos
да, т.к.
1;1
2
2
arccos 3
arccos( 3 )
arccos( 3 1)
2

7. Для чего нужен арккосинус?

х2=9
cost
=
х= 3
t = arccos
= π/6

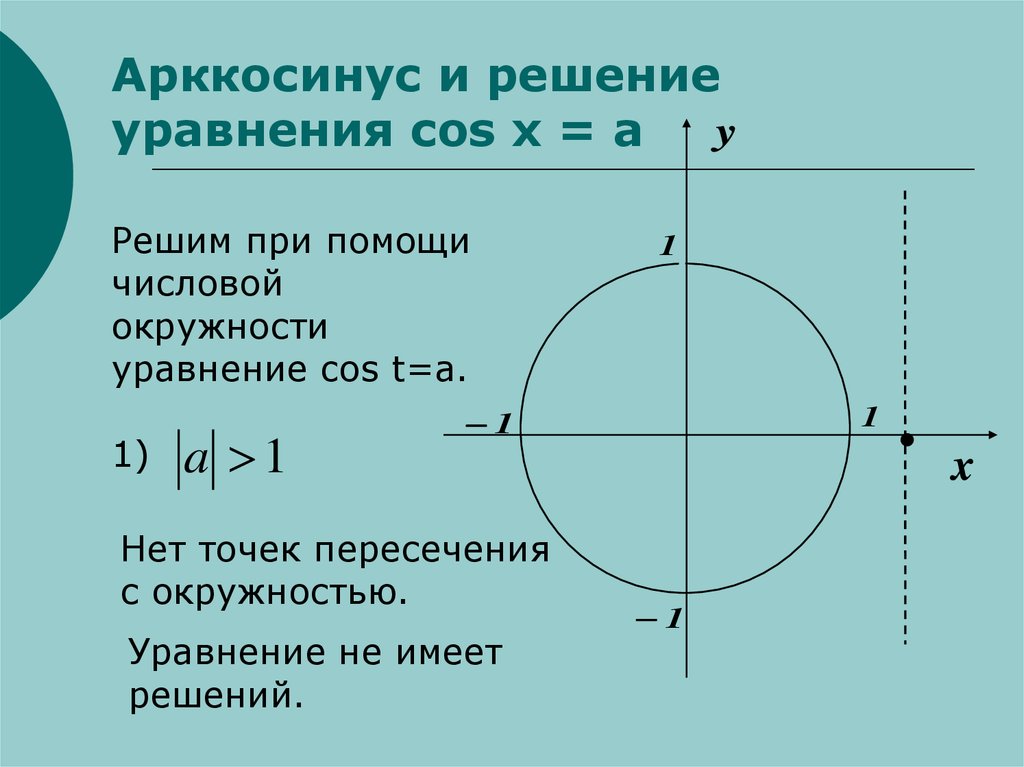
8. Арккосинус и решение уравнения cos x = a

Арккосинус и решение
y
уравнения cos x = a
Решим при помощи
числовой
окружности
уравнение cos t=a.
1)
a 1
1
1
Нет точек пересечения
с окружностью.
Уравнение не имеет
решений.
1
x
1

9. Арккосинус и решение уравнения cos x = a

y
Решим при помощи
числовой
окружности
уравнение cos t=a.
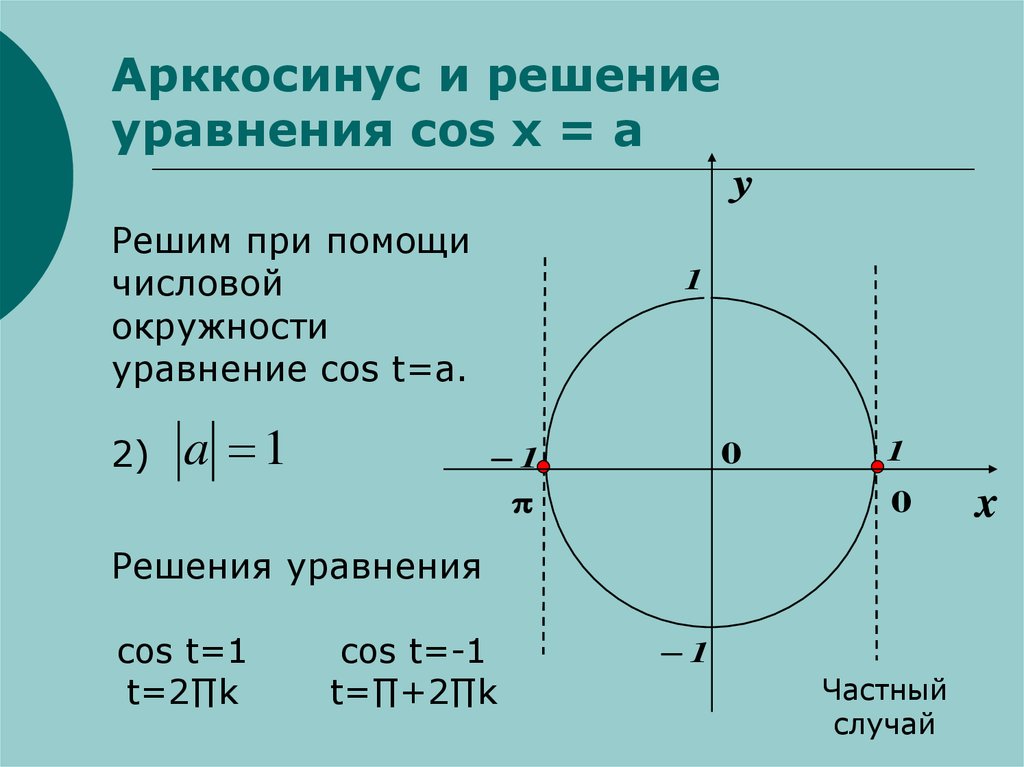
2)
a 1
1
1
0
1
0
Решения уравнения
cos t=1
t=2∏k
cos t=-1
t=∏+2∏k
1
Частный
случай
x

10. Арккосинус и решение уравнения cos x = a

y
Решим при помощи
числовой
окружности
уравнение cos t=a.
3) а=0
1
1 2
0
1
x
Решения уравнения
t
2
k
2
Частный
случай

11. Арккосинус и решение уравнения cos x = a

y
Решим при помощи
числовой окружности
уравнение cos t=a.
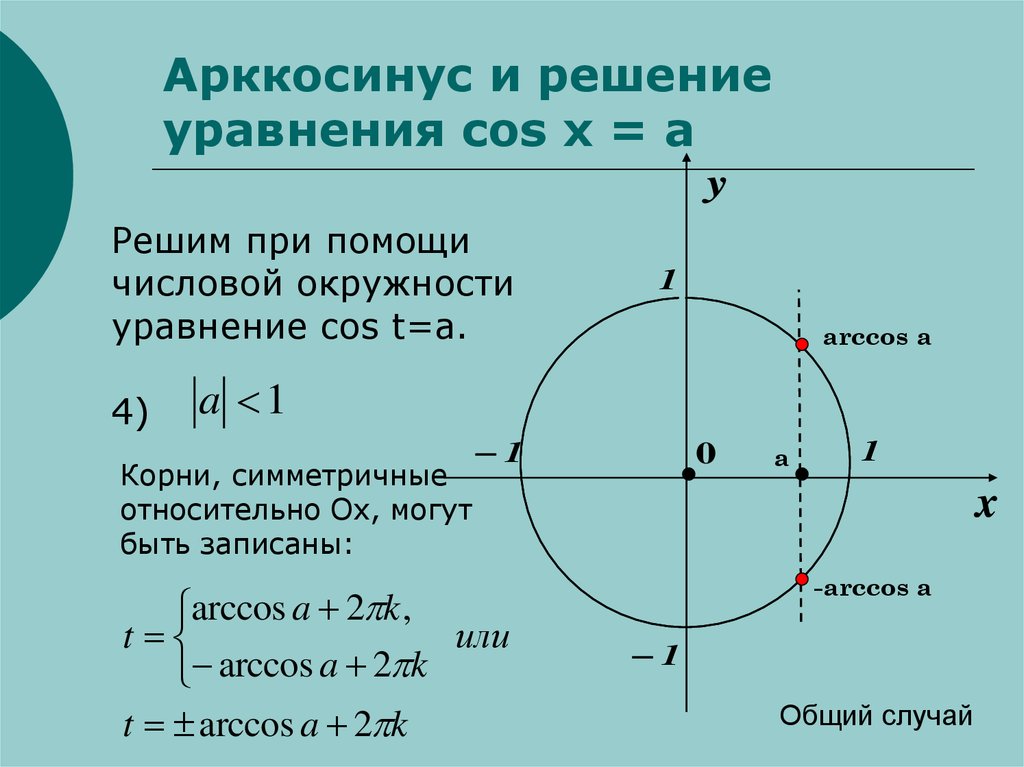
4)
1
arccos а
a 1
Корни, симметричные
относительно Оx, могут
быть записаны:
1
arccos a 2 k ,
t
или
arccos a 2 k
t arccos a 2 k
0
а
1
x
-arccos а
1
Общий случай

12. Арккосинус и решение уравнения cos x = a

Значение a
a 1
Решение
Нет решений
k
a 0
t
a 1
t 2 k
a 1
t 2 k
a 1
t arccos a 2 k
2

13. Выясните, верно ли равенство?

1
1
arccos , нет, т. к. 1) cos( ) , но 2) 0;
2
3
3
2
3
arccos 1
2
3
arccos(
)
2
4
3
arccos
2
6

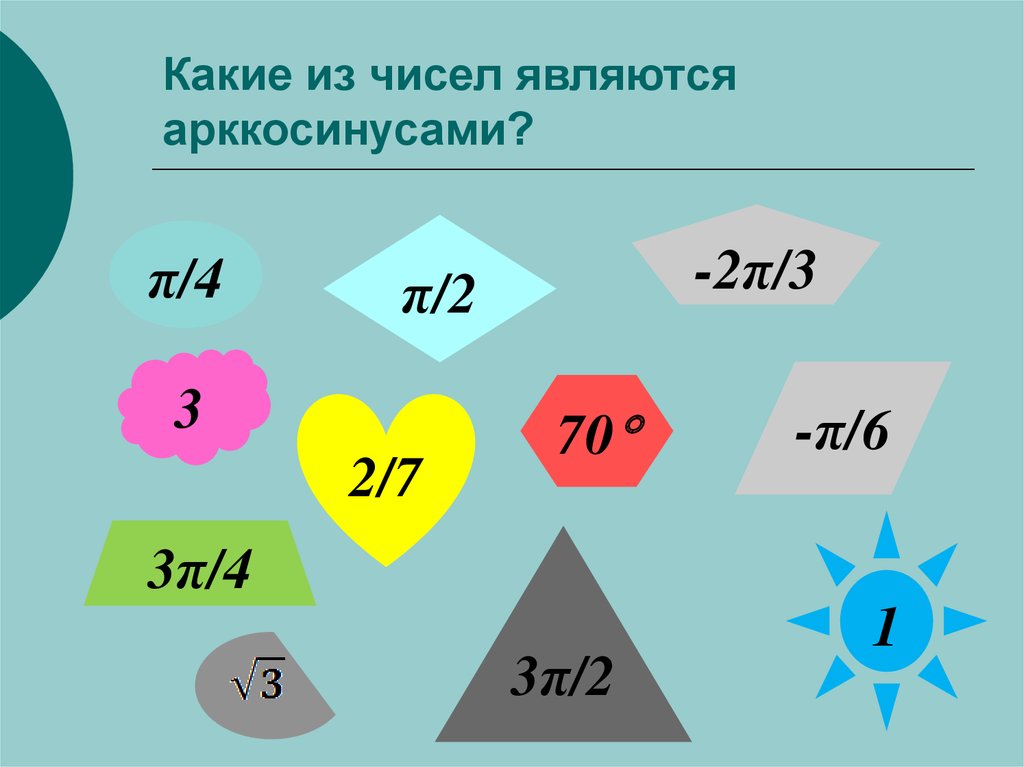
14. Какие из чисел являются арккосинусами?

π/4
-2π/3
π/2
3
2/7
70
-π/6
3π/4
3π/2
1

15. Основная задача –

свести любое
тригонометрические уравнение
к простейшему виду

16. Пример решения уравнения

cos 4x 0
cos 4x 0
t
4x k
2
Разделим обе части на 4
t
Это частный вид
уравнения cos t=a,
где a=0
x
8
k
4

17. Характерная грубая ошибка

cos 4x 0
Учащиеся делят обе части на 4
и получают следующее:
cos x 0
x
2
k

18. Пример решения уравнения

t
2 cos 4x 1 0
4x 2 k
4
2 cos 4x 1
Разделим обе части на 4
1
cos 4 x
2
k
x
16 2
1
4x arccos
2 k
2
k
x
16 2

19. Пример решения уравнения

cos 3x 0
3
Это частный вид
уравнения cos t=a, где
a=0
3x k
3
2
3x k
2 3
Уравнение уже имеет
простейший вид
3x k
6
k
x
18 3
k
x
18 3
t 3x
3
( 3)

20. Закрепление изученного материала

№ 289-291 (а, б)
№ 293 а, б
№ 294 а, б

21. Решение простейших тригонометрических неравенств

22.

3
cos t
2
y
6
2 k
3
2
0
1
x
6
2 k t
6
2 k
6
2 k

23.

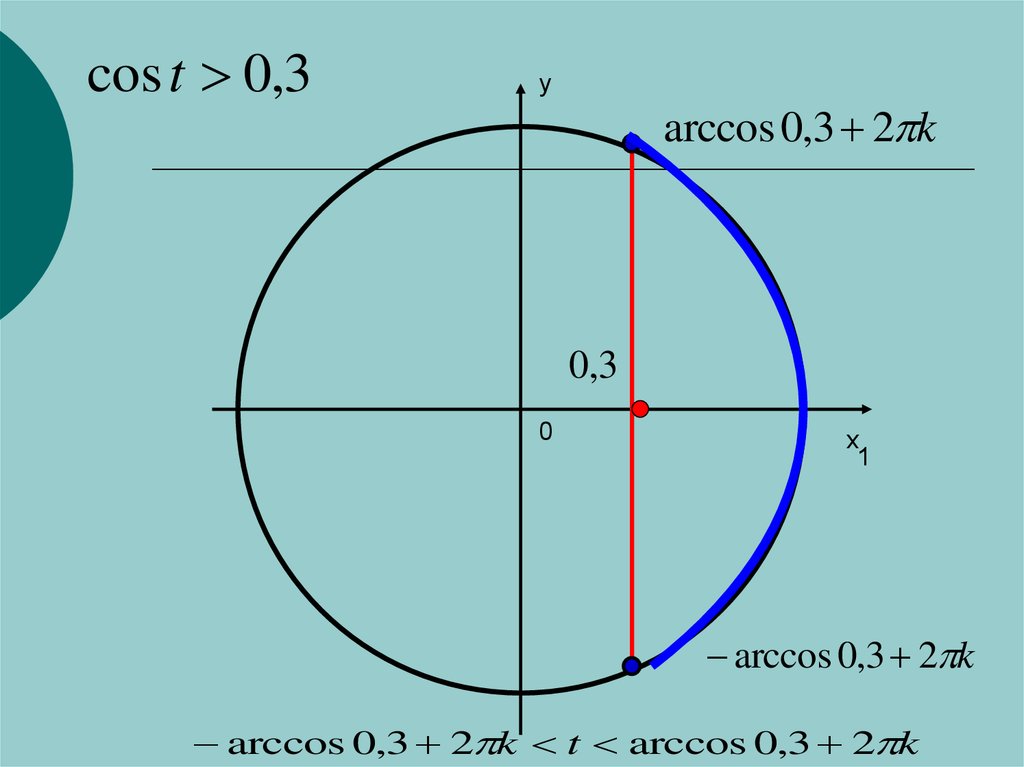
cos t 0,3
y
arccos 0,3 2 k
0,3
0
x
1
arccos 0,3 2 k
arccos 0,3 2 k t arccos 0,3 2 k

24. Закрепление изученного материала

№303 (а, г)
№ 304 (а, г)
№ 305 (а, г),
№ 306 (а, г).

25. Домашнее задание

Теория:
№ 291
№ 293
№ 294
№303
№ 304
№ 305
№ 306
стр. 75-81
(в, г)
(в, г)
(в, г)
(б, в)
(б, в)
(б, в)
(б, в)