Арккосинус. Решение уравнения cosx=a

1.

2.

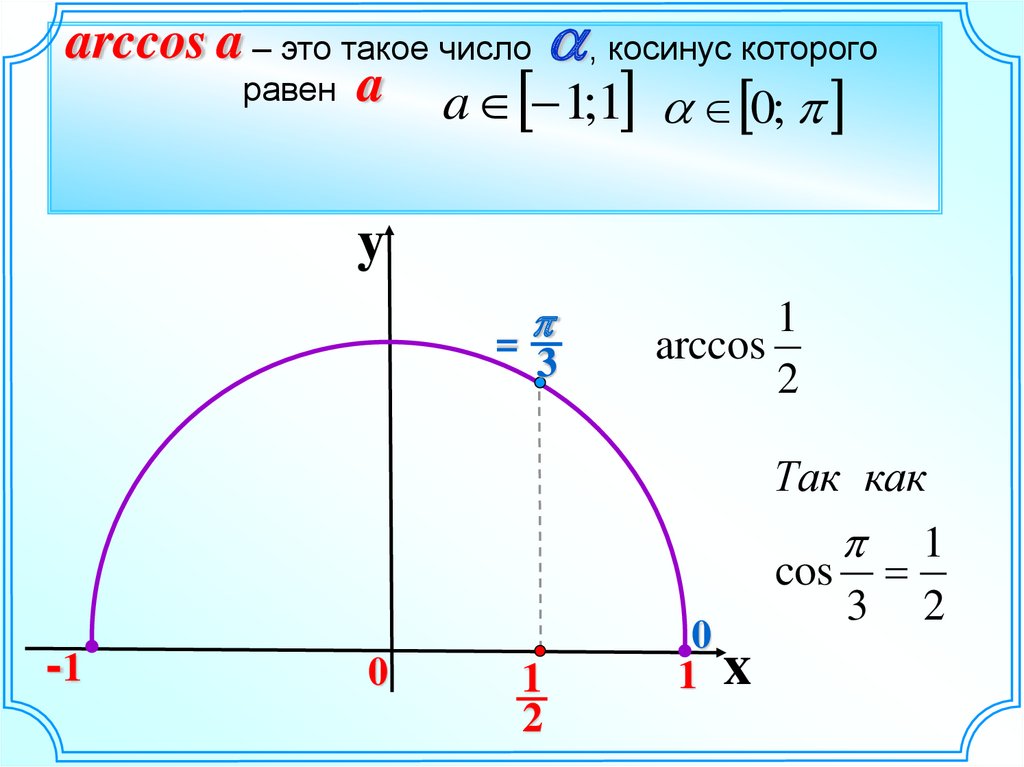
arccos a – это такое число a , косинус которого
равен a
a 1;1 a 0;
y
=
3
1
arccos
2
Так как
-1
0
1
2
0
1 x
1
cos
3 2

3.

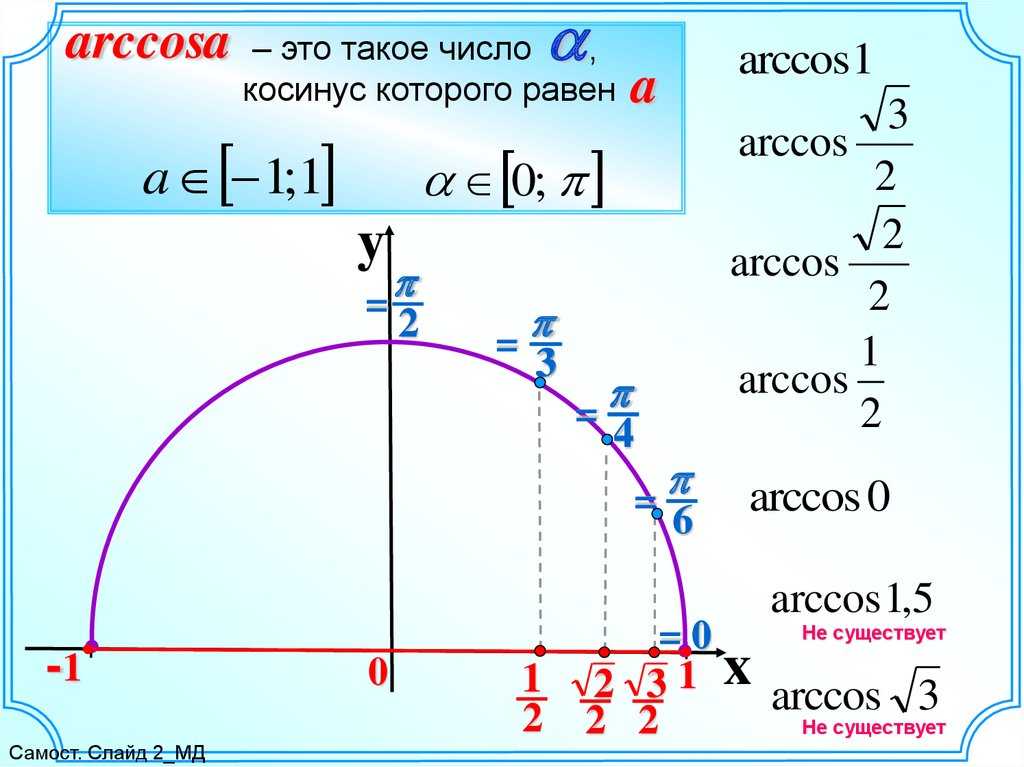
arccosa
a
– это такое число
,
косинус которого равен
a 1;1
arccos1
a
3
arccos
2
2
arccos
2
1
arccos
2
a 0;
y
=
2
=
3
=
4
=
6
arccos 0
arccos 1,5
-1
Самост. Слайд 2_МД
0
1
2
Не существует
=0
2 3 1 x arccos 3
2 2
Не существует

4.

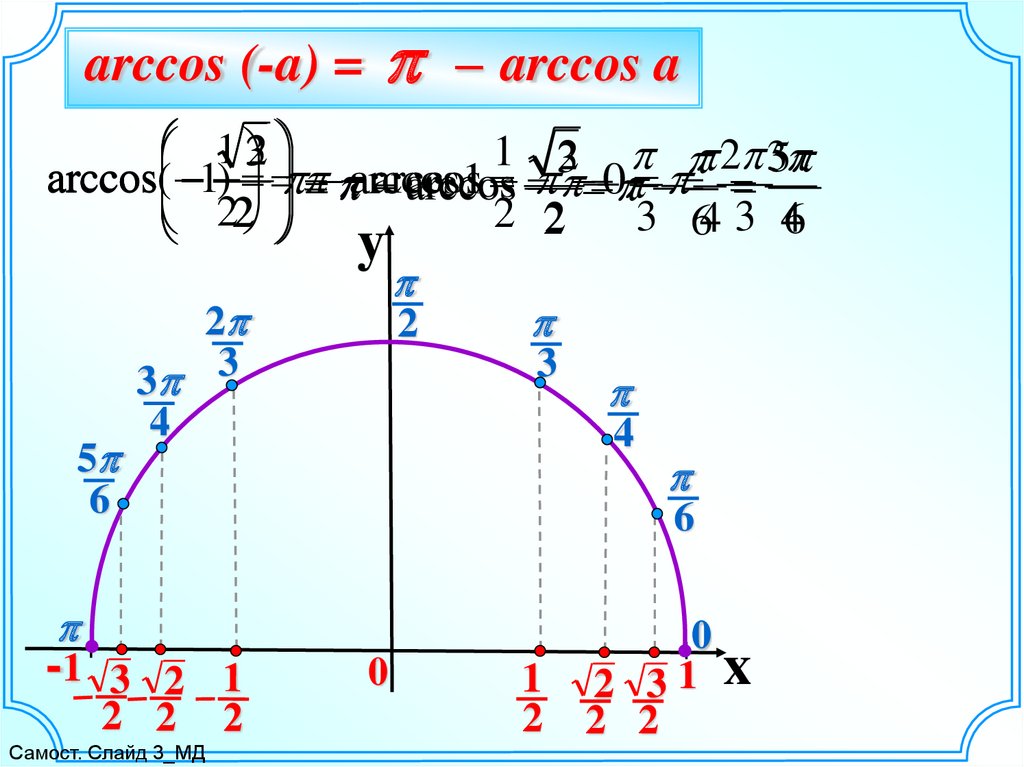
Для вычисления арккосинуса отрицательных чисел будем использовать
формулу
arccos (-a) = – arccos a
Используем графическую иллюстрацию для обоснования формулы:
y
arccosa
= arccos(-a)
-1
-a
arccosa
0
a
0
1 x

5.

arccos (-a) =
– arccos a
1 3 2
1 32 2 35
arccos
arccos( 1)
arccos
1 0
arccos
arccos
2 2
3 64 3 46
22 y
2
2
3
3 3
5
6
4
4
6
-1 3 2
2 2
Самост. Слайд 3_МД
0
1
2
0
2 31 x
2 2

6.

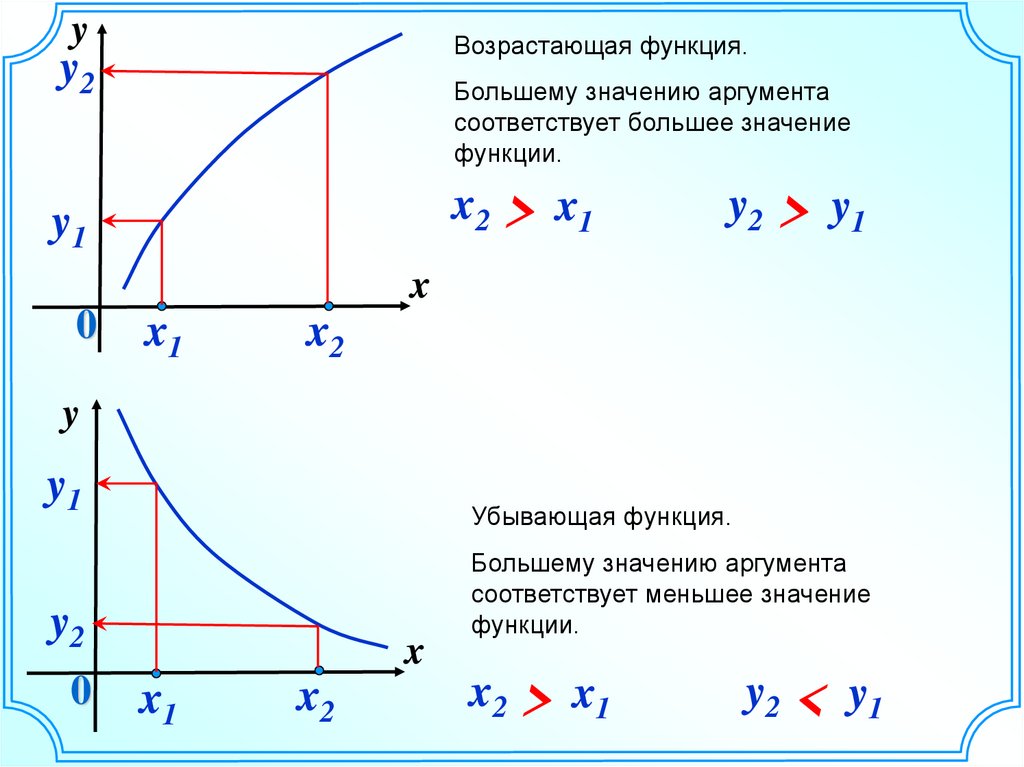
y
Возрастающая функция.
y2
Большему значению аргумента
соответствует большее значение
функции.
x2
y1
> x1
y2
> y1
x
0
x1
x2
y
y1
Убывающая функция.
y2
0
x
x1
x2
Большему значению аргумента
соответствует меньшее значение
функции.
x2
> x1
y2
< y1

7.

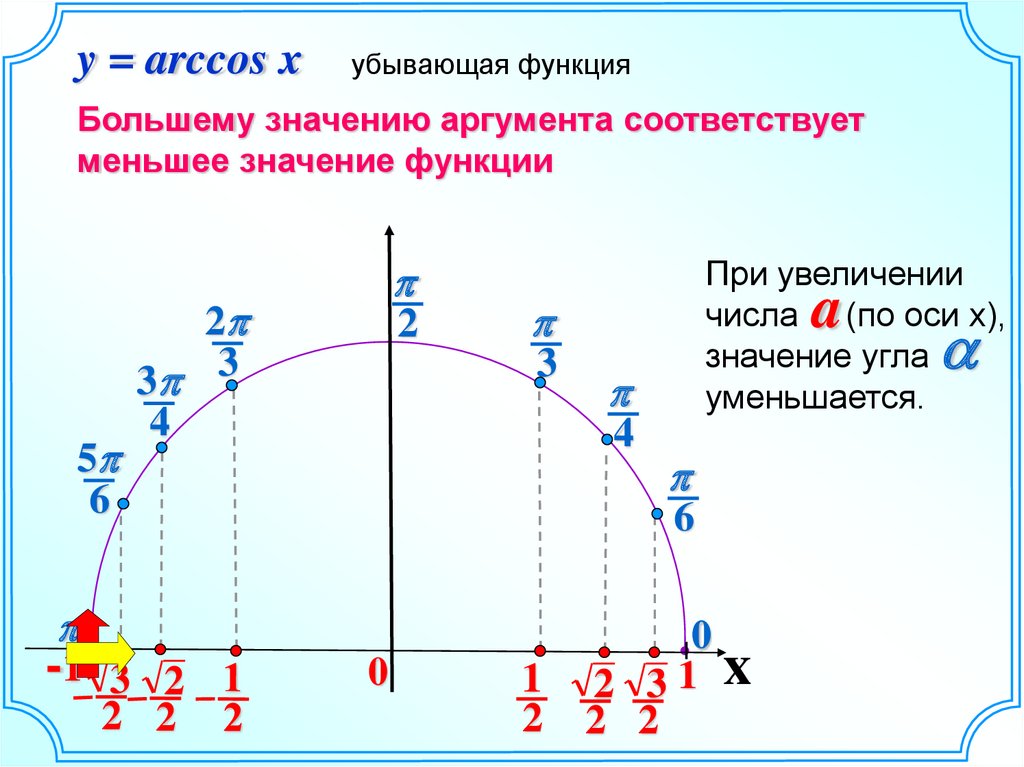
y = arccos x
убывающая функция
Большему значению аргумента соответствует
меньшее значение функции
5
6
2
3 3
4
2
2 2
a
3
4
6
-1 3 2
При увеличении
числа (по оси х),
значение угла
уменьшается.
0
1
2
0
2 31 x
2 2
a

8. АРККОСИНУС ЧИСЛА

2
arccos
;
2
4
arccos0
2
3
arccos
;
6
2
т.к.
т.к.
т.к.
2
0 ; cos
.
4
4
2
0
2
; cos
2
0.
3
0 ; cos
.
6
6
2

9. АРККОСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ

2
1
1. 3 arccos 2 2 arccos 2
2
1
3 arccos
2( arccos ) 3 2 ( )
2
2
4
3
7
3 4
12
4
3
1
3
1
2. arccos
2 arccos( 1) arccos0
2
2
3
1 5
17
1
3
1
2
( arccos ) 2
2
2
3 2 2 6
6
12

10.

Сравнить
1
1
arccos < arccos( )
4
4
3
arccos < arccos( 1)
4
5
7
arccos
> arccos( )
3
3
1
1
4
4
3
1
4
arccos 0,3 > arccos( 0,1)
0,3 0,1
arccos 0,9 > arccos( 0,34)
0,9 0,34
Самост. Слайд 4_МД
5
7
3
3

11.

АРККОСИНУС ЧИСЛА
ОСНОВНЫЕ ФОРМУЛЫ
cos arccosa a, arccosa 0; , a 1;1
arccos a arccosa
arccos cosa a ,a 0;
2
sin arccosa 1 a
1 a
tg(arccos a)
a
2

12. АРККОСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ

cos(arccos a) = a
2
1. cos arccos
2
5 5
2. cos arccos
9 9
2
2
3
sin
3. sin arccos
2
6
4.
3
sin arccos
7
40
49
2 10
7
1
2
sin arccosa 1 a 2
2
3
1
7
9
1
49

13.

Определим, имеют ли смысл выражения:
Выражение имеет смысл, если удовлетворяет условию
1) arccos (√5) - выражение не имеет смысла, так как √5 > 1;
2) arccos (√2/3) - выражение имеет смысл, так как – 1
√2/3
1;
3) arccos (-π/5) - выражение имеет смысл, так как – 1
- π /5
1;
4) arccos (-√3) - выражение не имеет смысла, так как -√3 < -1.

14. При каких значениях х имеет смысл выражение:

1. arccos(x²-1)
-1≤ х²-1 ≤ 1
0 ≤ х² ≤2
Ответ:
2.arccos(5-2x)
-
1≤ 5-2х ≤1
-6≤ -2х ≤ -4
2≤ х ≤3
Ответ: [2;3]

15.

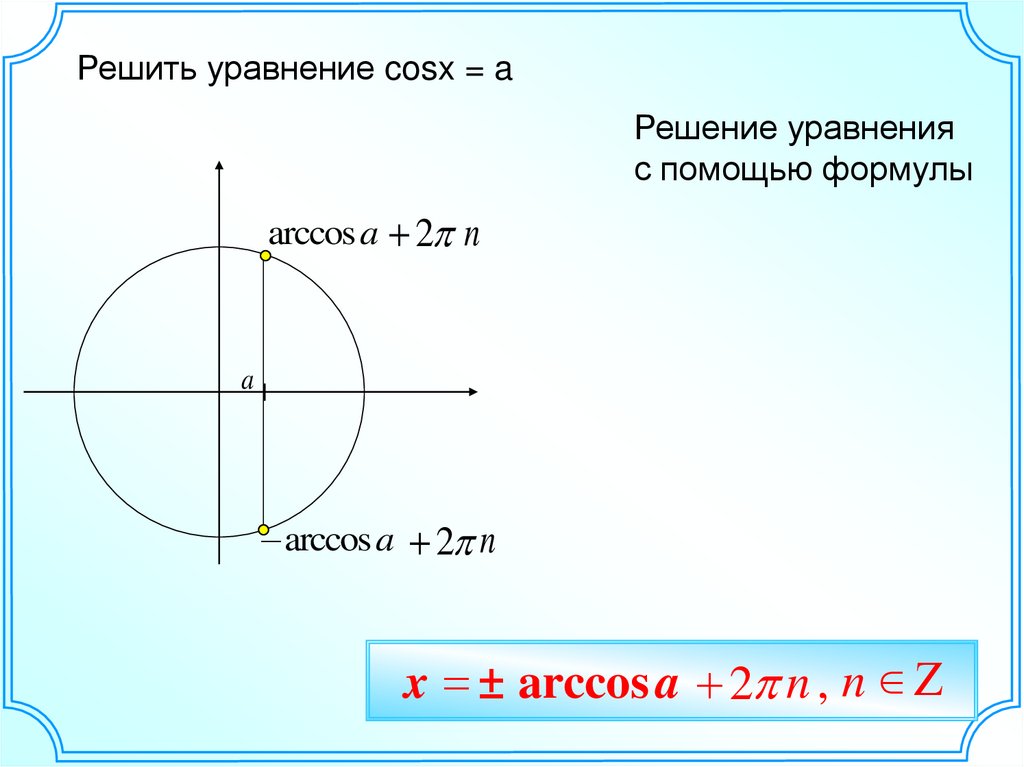
Решить уравнение cosx = a
Решение уравнения
с помощью формулы
arccos a 2 n
a
arccos a 2 n
x ± arccos a 2 n , n Z

16.

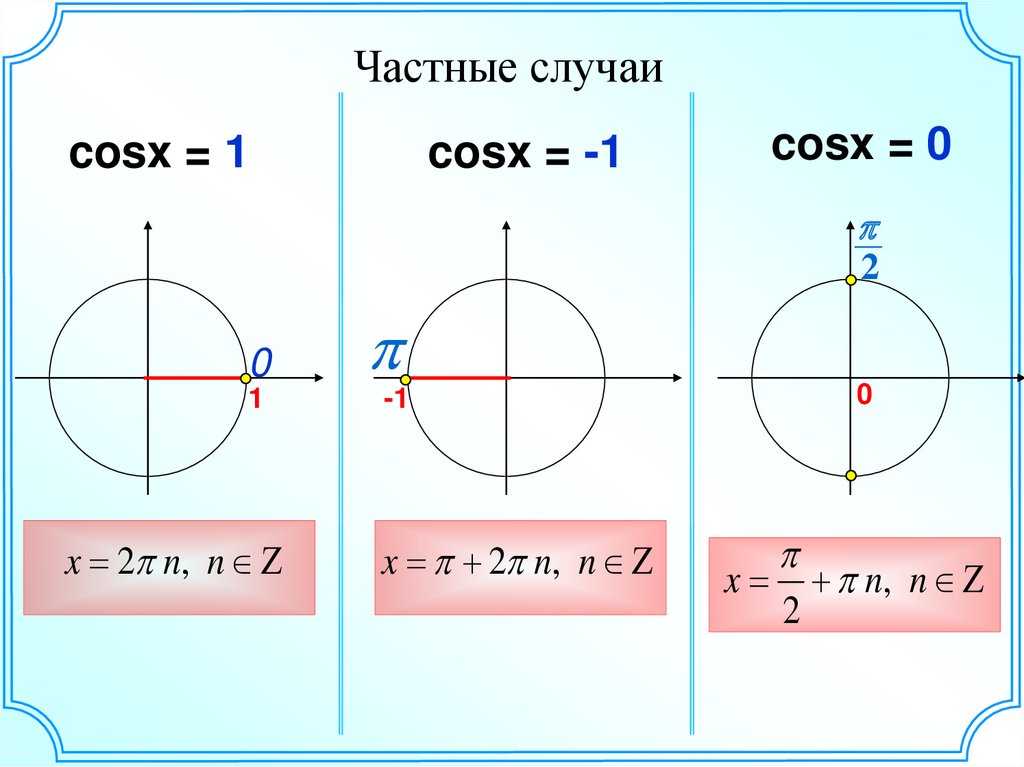
Частные случаи
cosx = 1
cosx = -1
cosx = 0
2
0
1
-1
x 2 n, n Z
x 2 n, n Z
0
x n, n Z
2

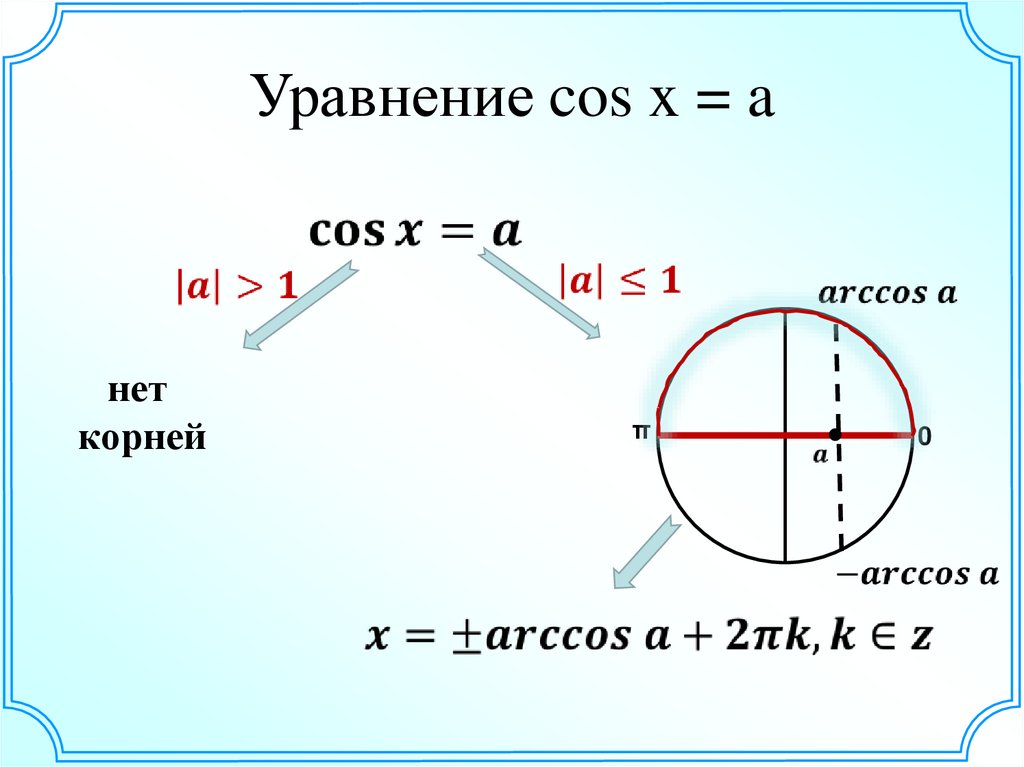
17. Уравнение cos x = a

нет
корней
π
0

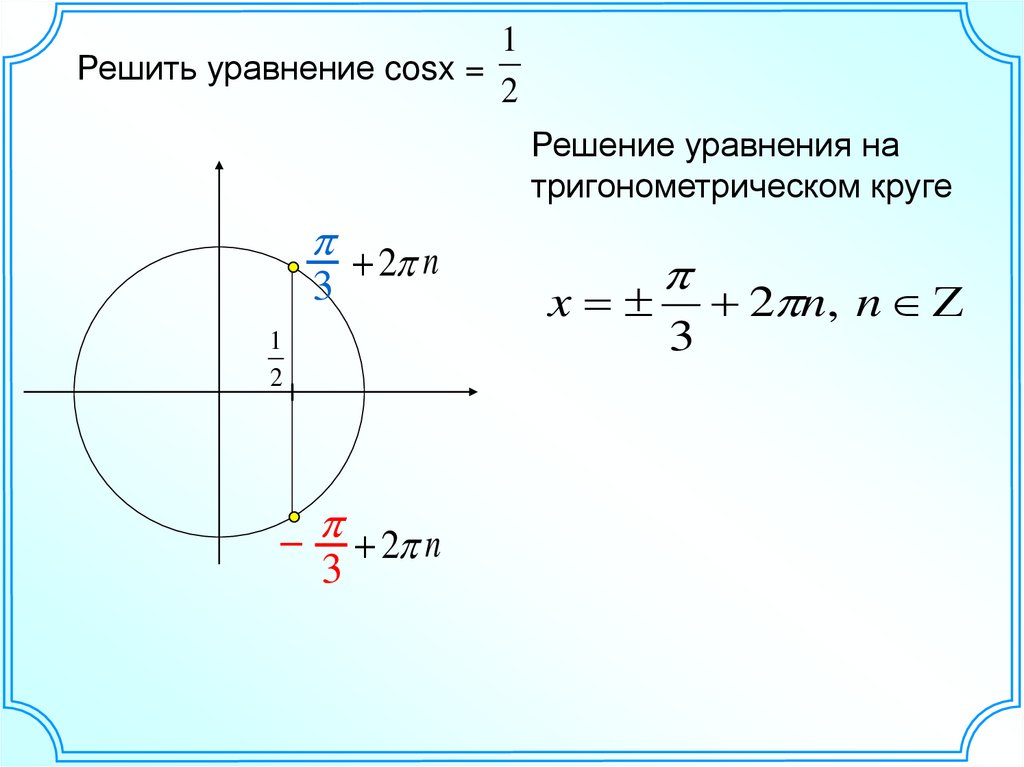
18.

1
Решить уравнение cosx =
2
Решение уравнения на
тригонометрическом круге
2 n
3
1
2
– 2 n
3
x
3
2 n, n Z

19.

1
Решить уравнение cosx =
2
2 2 n
3
1
2
4 2 n
3
Решение уравнения на
тригонометрическом круге
x (
3
) 2 n, n Z
2
x (
) 2 n, n Z
3

20.

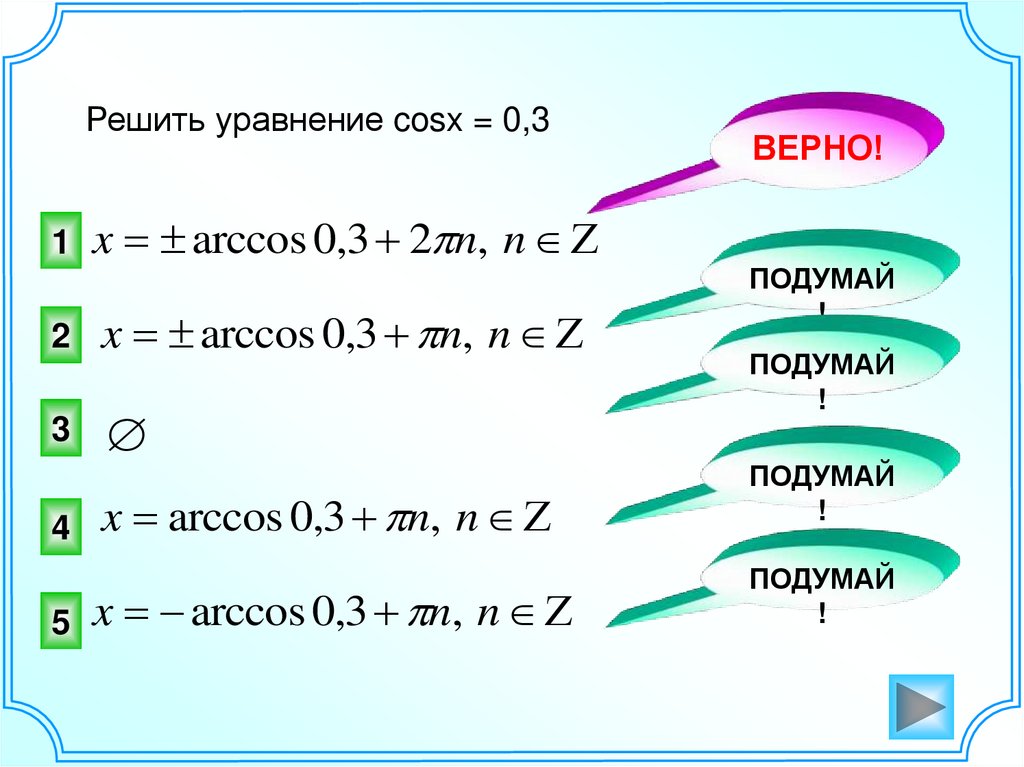
Решить уравнение

21.

Решить уравнение cosx = 0,3
1
x arccos 0,3 2 n, n Z
2
x arccos 0,3 n, n Z
3
4
5
x arccos 0,3 n, n Z
x arccos 0,3 n, n Z
ВЕРНО!
ПОДУМАЙ
!
ПОДУМАЙ
!
ПОДУМАЙ
!
ПОДУМАЙ
!

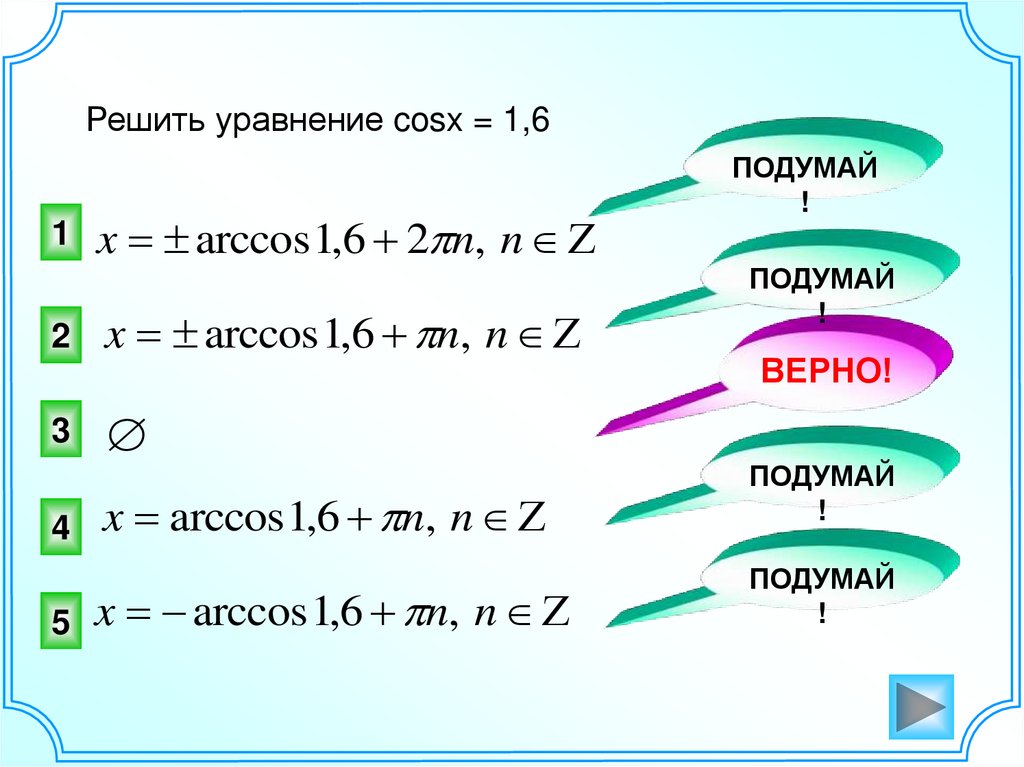
22.

Решить уравнение cosx = 1,6
1
x arccos 1,6 2 n, n Z
2
x arccos 1,6 n, n Z
3
4
5
x arccos 1,6 n, n Z
x arccos 1,6 n, n Z
ПОДУМАЙ
!
ПОДУМАЙ
!
ВЕРНО!
ПОДУМАЙ
!
ПОДУМАЙ
!

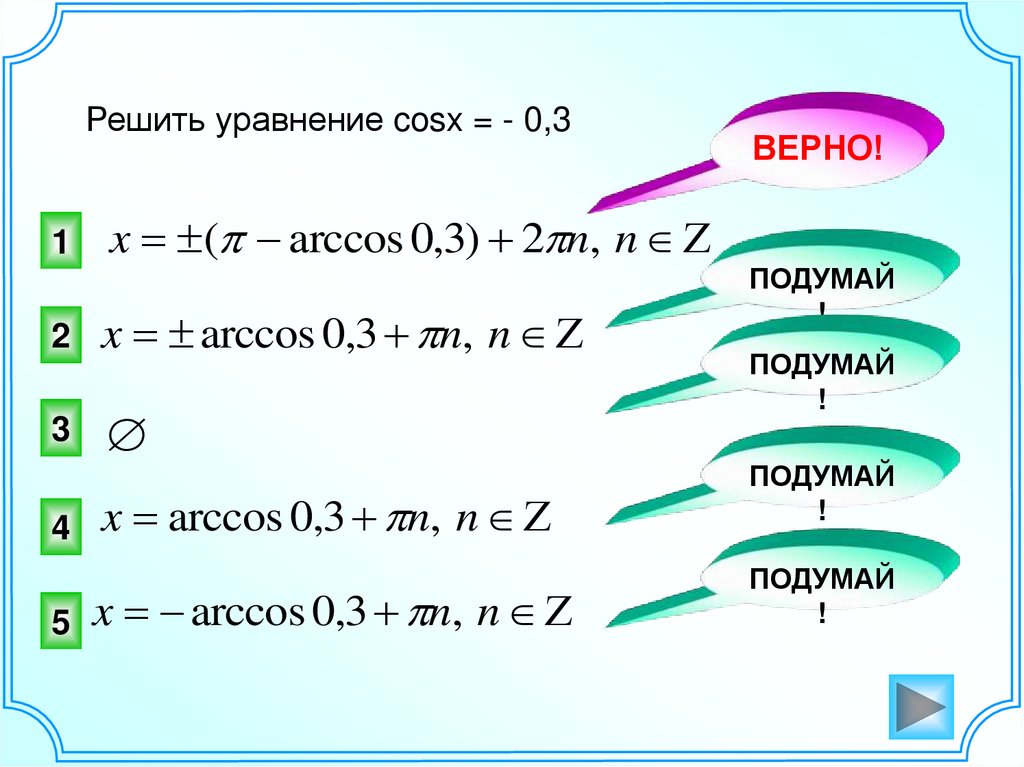
23.

Решить уравнение cosx = - 0,3
1
x ( arccos 0,3) 2 n, n Z
2
x arccos 0,3 n, n Z
3
4
5
ВЕРНО!
x arccos 0,3 n, n Z
x arccos 0,3 n, n Z
ПОДУМАЙ
!
ПОДУМАЙ
!
ПОДУМАЙ
!
ПОДУМАЙ
!

24. Уравнение cosx=a

1
cos3x ;
2
1
3x arccos 2 k ;
2
3 x 2 k ;
3
2 k
x
, k Z.
9
3

25. Уравнение cosx=a

x
3
сos ;
4
2
x
3
2 k ;
arccos
4
2
x
3
arccos 2 k ;
4
2
x
2 k ;
4
6
x
5
2 k ;
4
6
10
x 8 k , k Z .
3

26. Уравнение cosx=a

1
cos x
4
2
1
x arccos
2 k ;
4
2
1
x arccos 2 k ;
4
2
x 2 k ;
4 4
x 2 k
3
x 2 k ;
, k Z.
x 2 k
4
4
2

27. Уравнение cosx=a

3sin 2 x 3 2 cos x 1 0
3sin 2 x 3 0;
sin 2 x 1;
2x
x
2
4
2 k ;
k , k Z .
2 cos x 1 0;
1
cos x ;
2
1
x arccos 2 n;
2
x 2 n;
3
2
x 2 n, n Z .
3

28. Уравнение cosx=a

cos5x cos7 x cos 6 x
cos5x cos7 x cos6 x
2 cos6 x cos x cos6 x 0
cos6 x 2 cos x 1 0
cos6 x 0
2
cos
x
1
0
6x
2
n, n Z
x n, n Z
12 6
1
cos x
2
2
x
2 k ;
3