Проект по теме «Теорема синусов»

1. Проект по теме «Теорема Синусов»

Ученика 9 «Б»
Самошкина Артёма

2.

Теоре́ма си́нусов — теорема,
устанавливающая зависимость между
длинами сторон треугольника и величиной
противолежащих им углов. Существуют два
варианта теоремы;

3. Обычная теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.

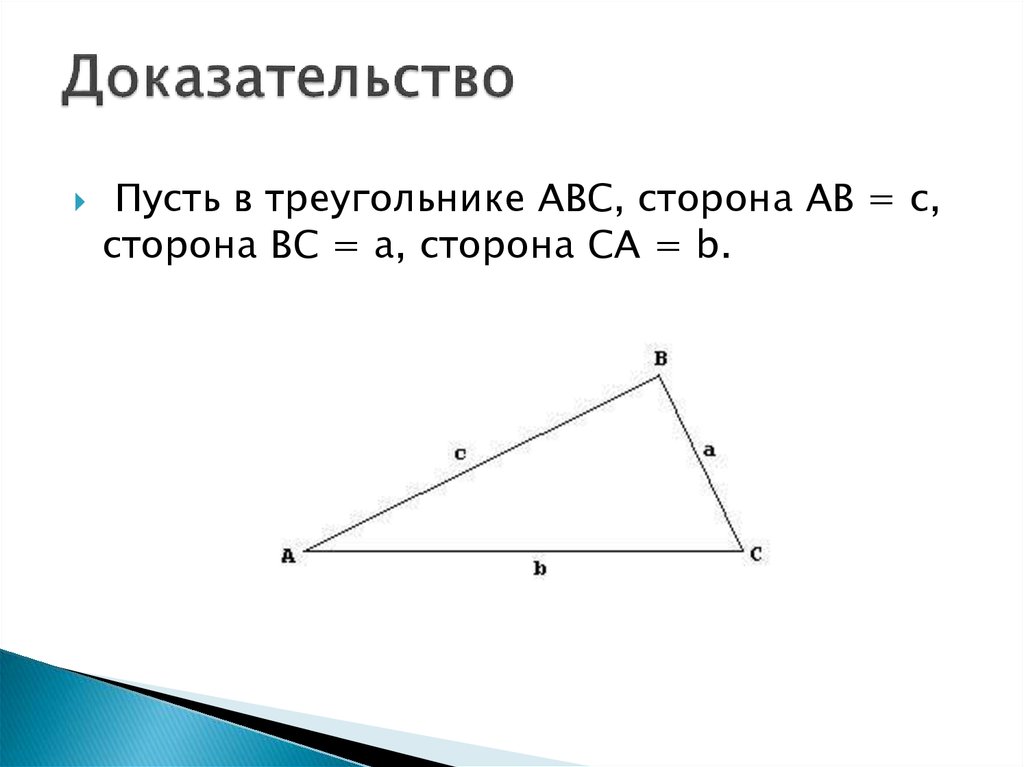
4. Доказательство

Пусть в треугольнике ABC, сторона AB = c,
сторона BC = a, сторона CA = b.

5.

Попытаемся доказать, что a/sin(A) = b/sin(B) = c/sin(C). Воспользуемся
теоремой о площади треугольника, и запишем её для каждой пары сторон и
соответствующего им угла:
S = (1/2)*a*b*sin(C),
S = (1/2)*b*c*sin(A),
S = (1/2)*c*a*sin(B).
Так как левые части у первых двух равенств одинаковые, то правые части
можно приравнять между собой. Получим (1/2)*a*b*sin(C) = (1/2)*b*c*sin(A).
Сократим это равенство на ½*b, получим:
a*sin(C) = c*sin(A).
По свойству пропорции получаем:
a/sin(A) = c/sin(C).
Так как левые части у второго и третьего равенств одинаковые, то правые
части можно приравнять между собой. Получим (1/2)*b*c*sin(C) =
(1/2)*c*a*sin(B). Сократим это равенство на 1/2*c, получим:
b*sin(A) = a*sin(B).
По свойству пропорции получаем:
a/sin(A) = b/sin(B).
Объединив полученные два результата получаем: a/sin(A) = b/sin(B) = c/sin(C).
Что и требовалось доказать.

6. Расширенная теорема синусов:

Для произвольного треугольника
a/sin(A) =b/sin(B) = c/sin(C) = 2*R.
где a,b,c—стороны треугольника, —
соответственно противолежащие им
углы, — радиус окружности, описанной
около треугольника.

7.

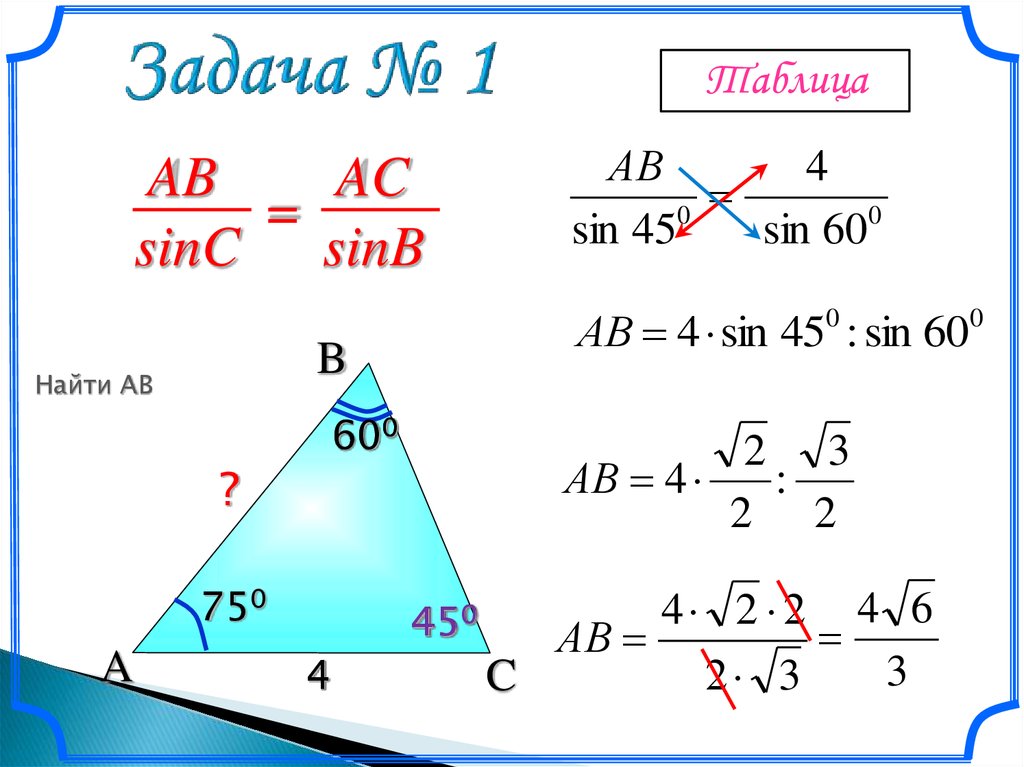
Таблица
AB
AC
=
sinC sinB
АВ
4
0
sin 45
sin 600
АВ 4 sin 45 : sin 60
0
B
Найти АВ
600
?
750
A
2 3
АВ 4
:
2 2
450
4
4 2 2 4 6
АВ
3
2 3
C
0

8.

2
3
0
sin С
sin 60
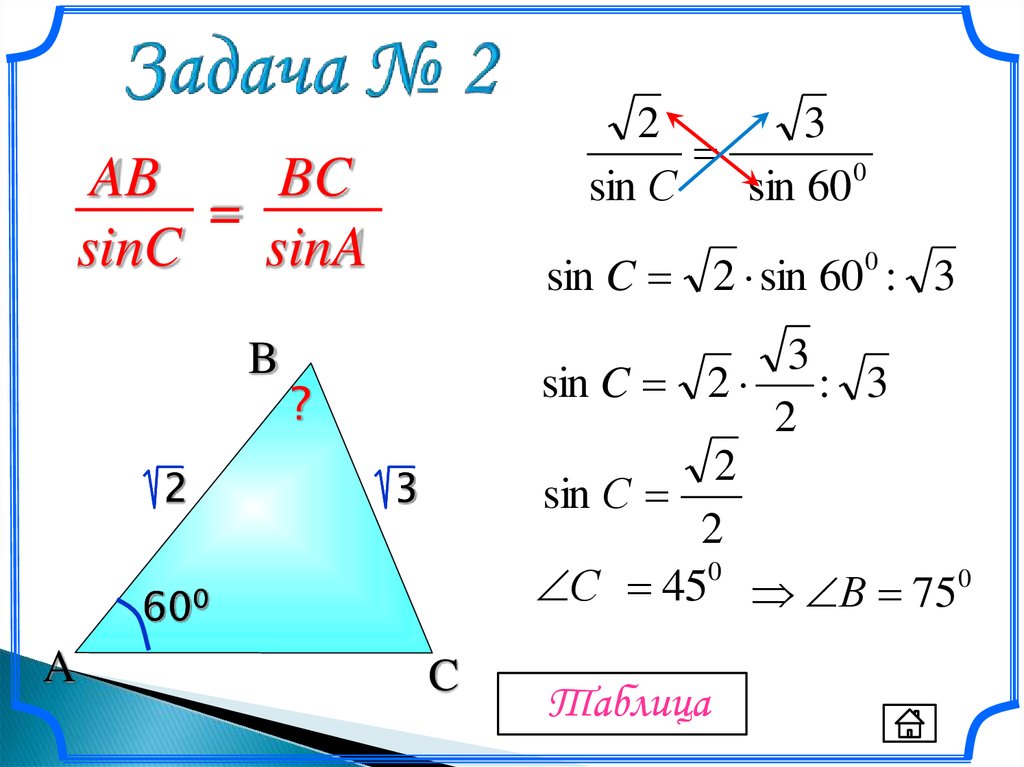
AB
BC
=
sinC sinA
B
2
sin C 2 sin 60 : 3
0
3
sin C 2
: 3
2
2
sin С
2
0
С 45 В 750
?
3
600
A
C
Таблица

9.

2 2
2
0
sin 135
sin В
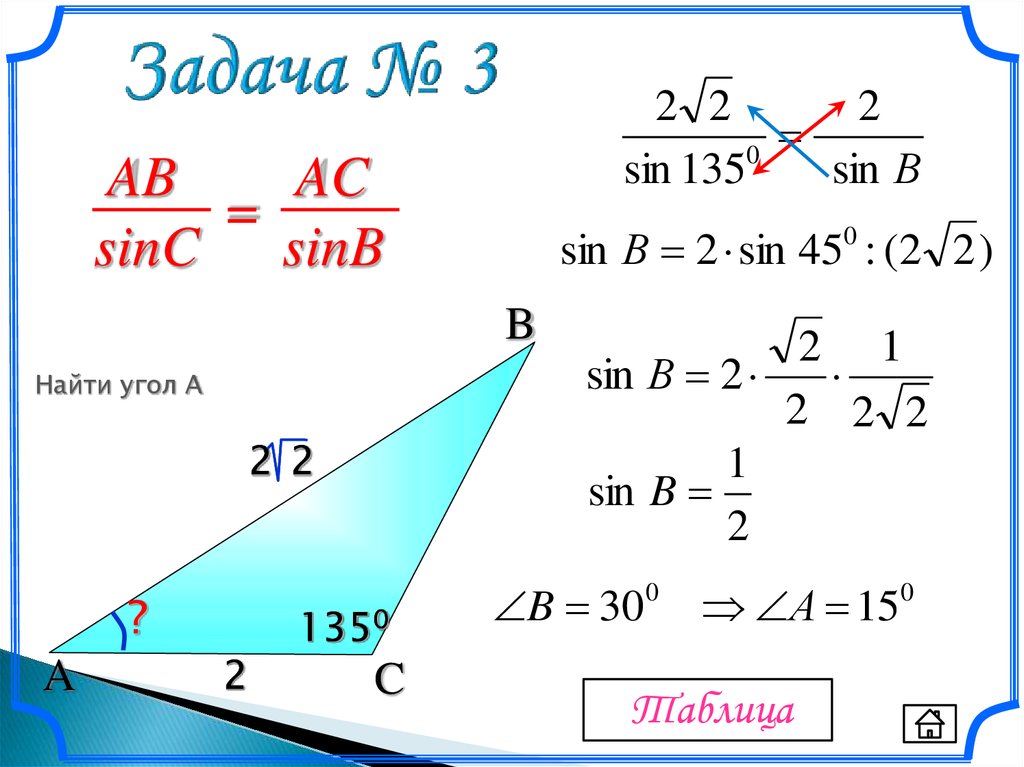
AB
AC
=
sinC sinB
sin В 2 sin 450 : (2 2 )
B
Найти угол А
2 2
?
A
2
1350
C
2 1
sin В 2
2 2 2
1
sin B
2
B 300 А 150
Таблица

10.

Спасибо
за внимание!