Похожие презентации:
Производная функции
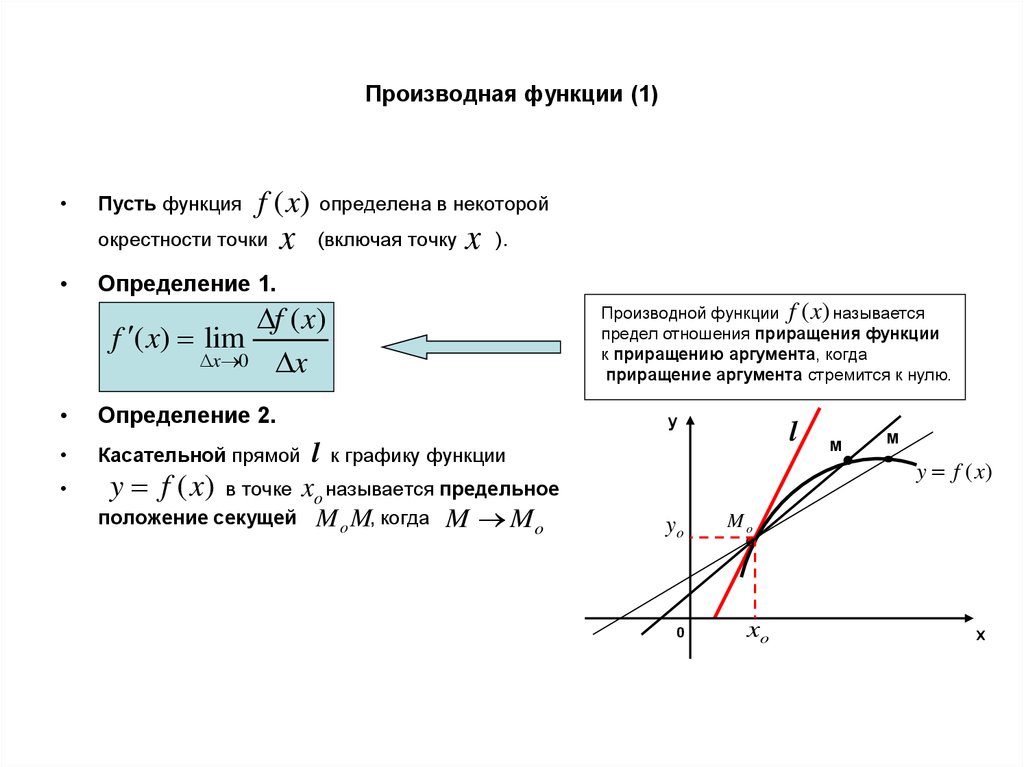
1. Производная функции (1)
Пусть функция
f (x)
окрестности точки
x
определена в некоторой
(включая точку
x
).
Определение 1.
f ( x)
f ( x) lim
x 0 x
Определение 2.
Касательной прямой
в точке
положение секущей
y f (x)
Производной функции f (x) называется
предел отношения приращения функции
к приращению аргумента, когда
приращение аргумента стремится к нулю.
y
l
l к графику функции
xo называется предельное
M o M, когда M M o
M
M
y f (x)
yo
0
Mo
xo
х
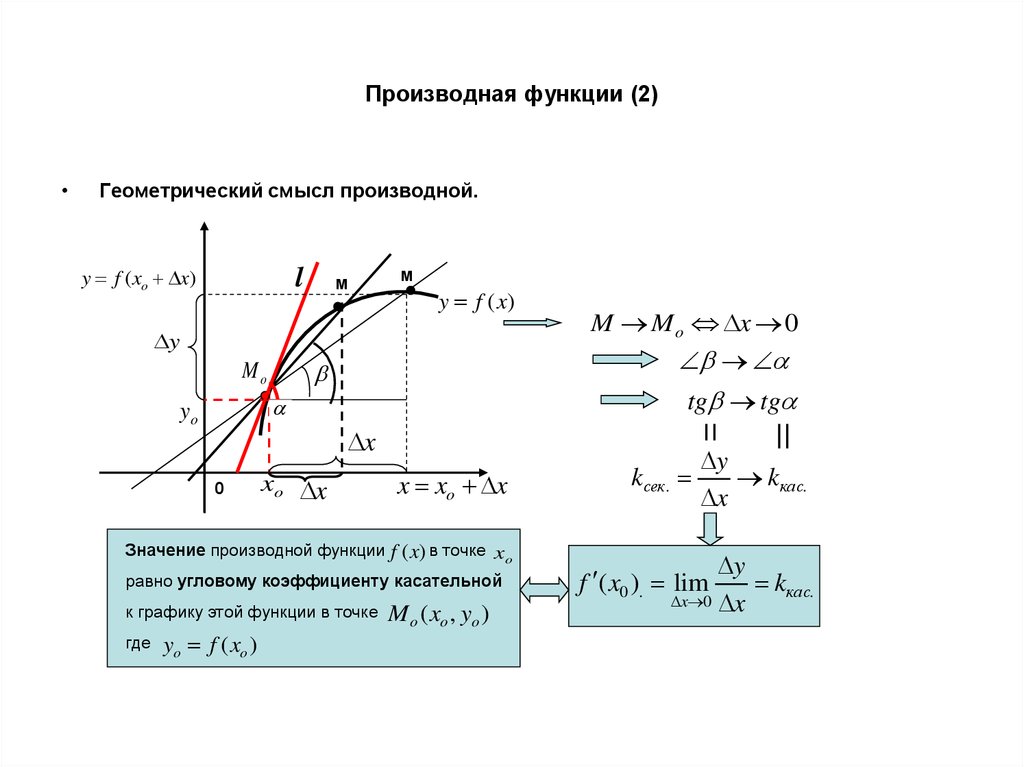
2. Производная функции (2)
Геометрический смысл производной.
y f ( xo x)
l
M
M
y f (x)
y
Mo
tg tg
yo
x
0
xo x
x xo x
Значение производной функции f (x) в точке xo
равно угловому коэффициенту касательной
к графику этой функции в точке
где
M M o x 0
yo f ( xo )
M o ( xo , yo )
kсек.
y
kкас.
x
y
kкас.
x 0 x
f ( x0 ). lim
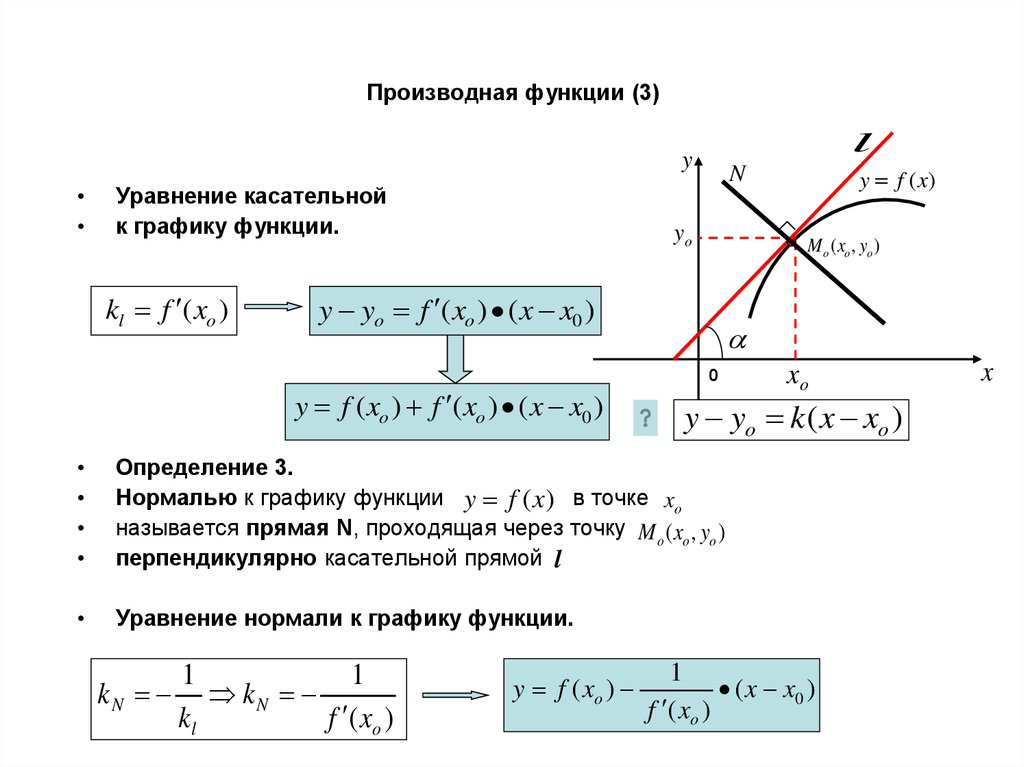
3. Производная функции (3)
ly
Уравнение касательной
к графику функции.
kl f ( xo )
N
yo
M o ( xo , yo )
y yo f ( xo ) ( x x0 )
0
y f ( xo ) f ( xo ) ( x x0 )
Определение 3.
Нормалью к графику функции y f (x) в точке xo
называется прямая N, проходящая через точку M o ( xo , yo )
перпендикулярно касательной прямой l
Уравнение нормали к графику функции.
y f ( xo )
xo
y yo k ( x xo )
1
1
kN kN
kl
f ( xo )
y f (x)
1
( x x0 )
f ( xo )
x
4. Производная функции (4)
Связь между существованием производной
– и непрерывностью функции.
–
Теорема.
f ( x) f ( x) непрерывнав т. x
–
Доказательство.
f ( x)
x 0 x
f ( x) lim
f ( x )
f ( x) ( x)
x
где 0 при х 0
f ( x) f ( x) x ( x) x
f ( x) 0 при x 0
f ( x) непрерывна в т. х
5. Производная функции (5)
Правила дифференцирования.
Пусть
Тогда
1.
2.
3.
4.
f ( x) и g ( x)
( f ( x) g ( x)) f ( x) g ( x)
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
(C f ( x)) C f ( x)
f ( x) f ( x) g ( x) f ( x) g ( x)
, если g ( x) 0
2
g ( x)
(
g
(
x
))
Доказательство 1 правила (для суммы).
1 шаг.
2 шаг.
3 шаг.
( f g ) f g
( f g ) f g
x
x x
( f g )
f
g
lim
lim
x 0
x 0 x
x 0 x
x
т о ест ь
( f ( x) g ( x)) f ( x) g ( x)
lim
6. Производная функции (6)
–Таблица производных основных
элементарных функций.
–
1.
(C ) 0
–
2.
( x ) n x
–
3.
–
4.
–
5.
–
6.
–
7.
–
–
–
n
n 1
(a x ) a x ln a
(e x ) e x
( x) 1
( x 2 ) 2 x
x 2 1 x
1
(loga x)
1 x ln a
(ln x)
x
(sin x) cos x
8. (cosx) sin x
1
9. (tg x)
cos2 x
1
(
ctg
x
)
10.
sin 2 x
11.
12.
13.
14.
(arcsin x)
(arccosx)
1
1 x2
1
1 x2
1
1 x2
1
(arcctgx)
1 x2
(arctgx)
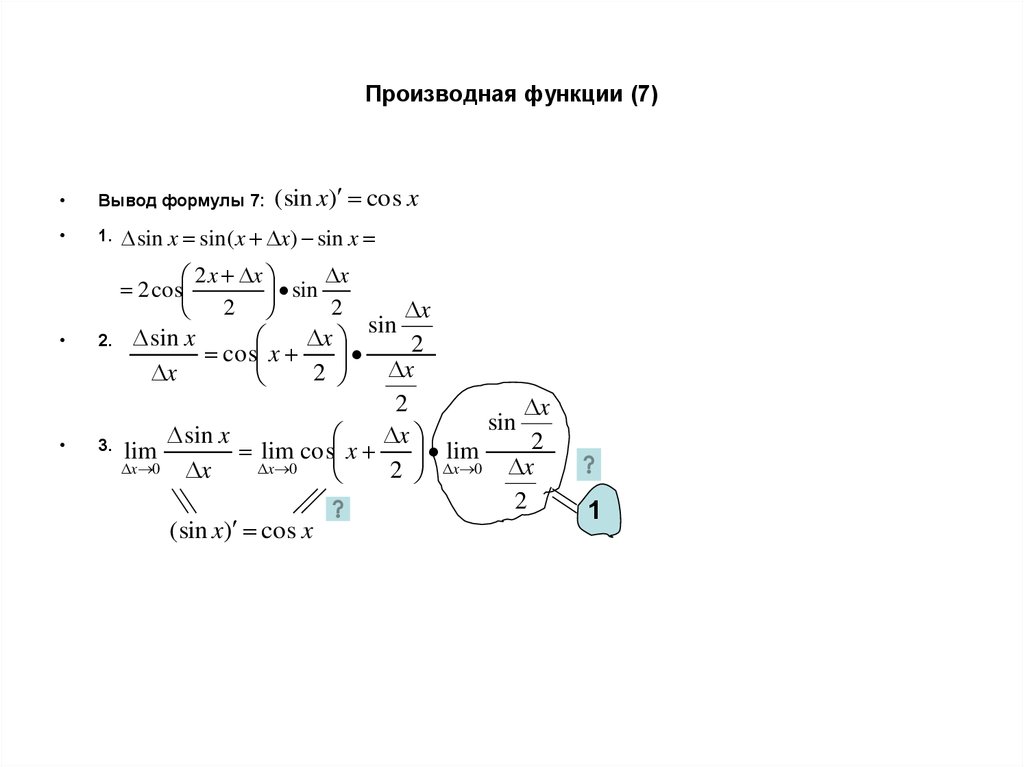
7. Производная функции (7)
Вывод формулы 7:
1.
(sin x) cos x
sin x sin(x x) sin x
x
2 x x
2 cos
sin
2
2
2.
3.
x
sin x
x
2
cos x
x
x
2
2
x
sin
sin x
x
2
lim
lim cos x
lim
x 0
x 0
x
2 x 0 x
2
(sin x) cos x
sin
1
8. Производная функции (8)
Производная сложной функции.
Теорема.
1. y(x) – сложная функция, то есть
y f (u ) , u ( x)
y( x) f ( ((x))
y ( x) f (u ) ( x)
где u ( x)
2. ( x) в т. х
3. f (u ) в т. u , причем
значение u ( x)
Доказательство.
1..Возьмем x 0 u y
(предполагаем, что u 0 )
y u
2. y
u x
y
y
u
lim
lim
lim
x 0 x
x 0 u x 0 x
y
u
lim
lim
u 0 u x 0 x
x
3.
(ч.т.д.)
9. Производная функции (9)
Примеры.
1.
y ln sin x
y ln u , u sin x
y
2.
1
1
cos x
cos x ctgx
u
sin x
y ln 2 sin x
y u 2 , u ln t , t sin x
1
1
y 2u cos x 2 ln sin x
cos x
t
sin x
2ctgx ln sin x
10. Производная функции (10)
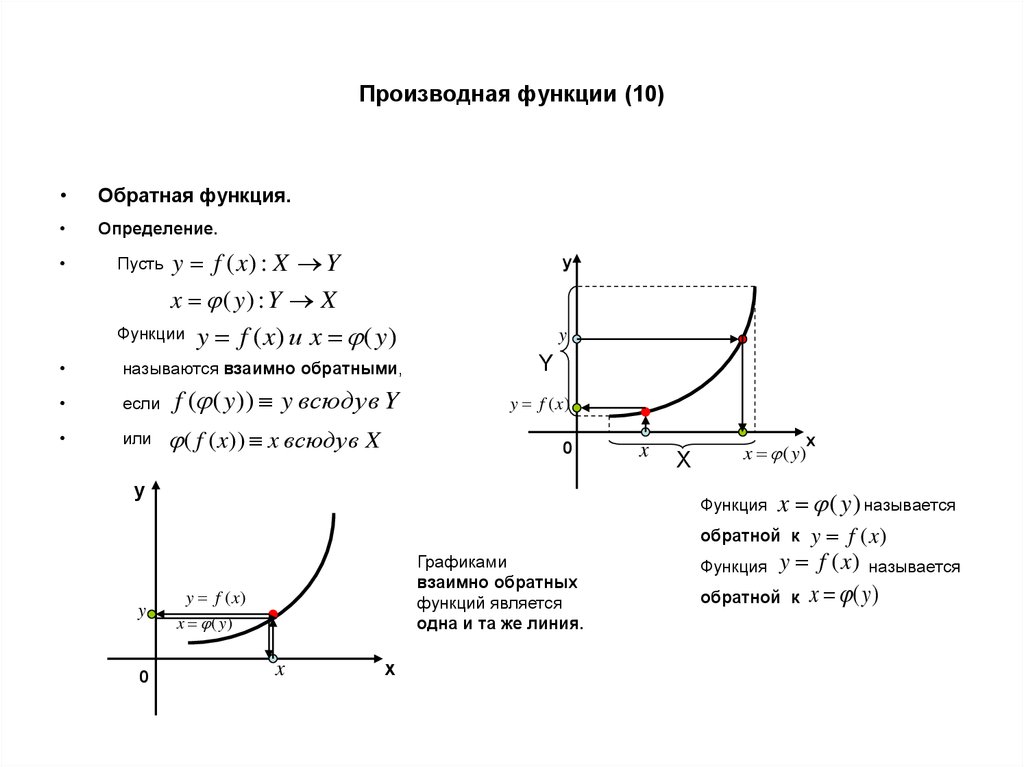
Обратная функция.
Определение.
y f ( x) : X Y
y
x ( y) : Y X
Функции y f ( x) и x ( y)
y
Пусть
называются взаимно обратными,
если
или
f ( ( y)) y всюду в Y
( f ( x)) x всюду в X
Y
y f (x)
0
y
x
х
X
x ( y)
Функция
x ( y) называется
обратной к
y
0
Графиками
взаимно обратных
функций является
одна и та же линия.
y f (x)
x ( y)
x
х
Функция
y f (x)
y f (x)
обратной к
называется
x (y)
11. Производная функции (13)
Производная обратной функции.
Теорема.
1.
2.
3.
y f ( x) непрерывна я на a, b ;
1.
f ( x) при x a, b и f ( x) 0
2.
y f ( x) монотонная на a, b ;
3.
Пример.
Вывод формулы 11 :
arcsin x
1.
2.
3.
x ( y ) обрат ная
к y f ( x) ;
x ( y) непрерывная
и монотонная;
( y) 1
f ( x)
1
1 x2
y arcsin x x sin y
1
1
x cos y y
x cos y
cos y 1 sin y 1 x
2
2
y
1
1 x2
( y )
2
1
1
f ( x)
f ( x)
( y )
y
2
cos y 0
12. Производная функции (14)
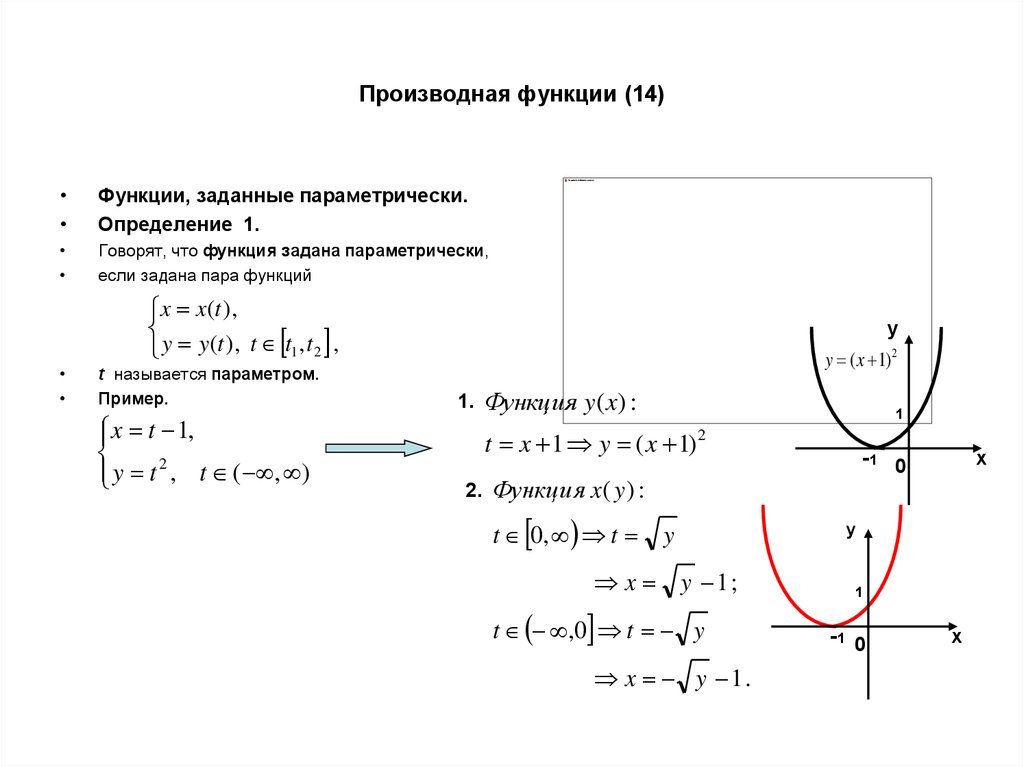
Функции, заданные параметрически.
Определение 1.
Говорят, что функция задана параметрически,
если задана пара функций
x x(t ),
y y (t ), t t1 , t 2 ,
t называется параметром.
Пример.
x t 1,
y t 2 , t ( , )
y
y ( x 1) 2
1.
Функция y( x) :
1
t x 1 y ( x 1) 2
2.
-1 0
Функция x ( y ) :
t 0, t
x
x
y
y
y 1;
t ,0 t y
x y 1.
1
-1 0
x
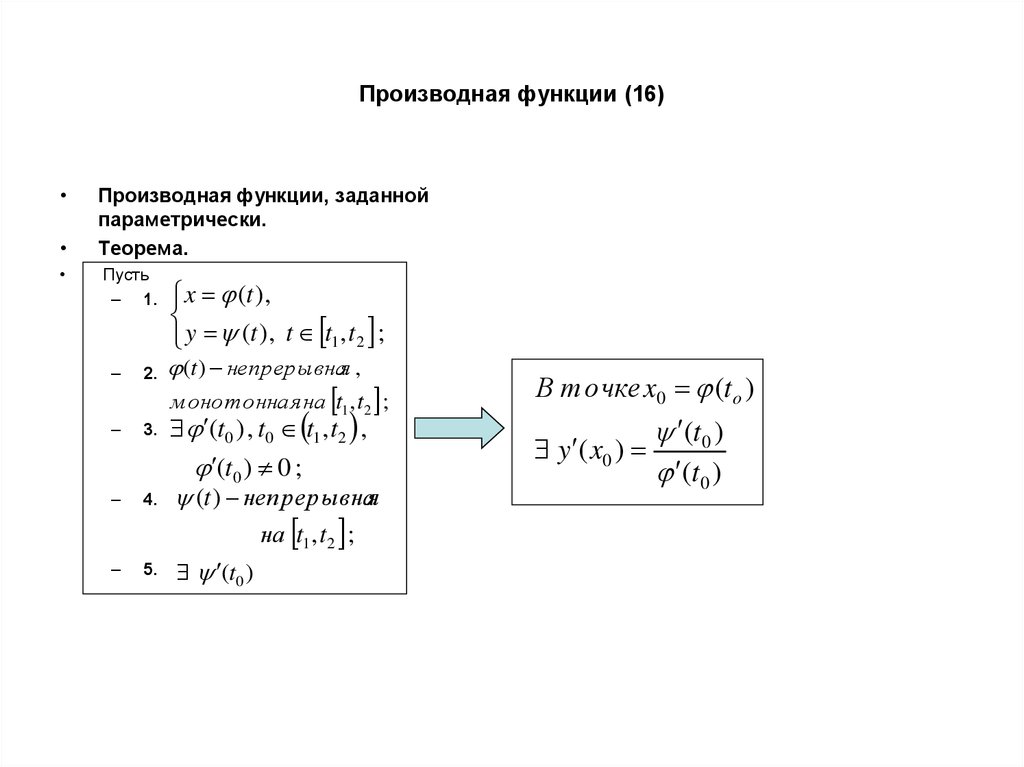
13. Производная функции (16)
Производная функции, заданной
параметрически.
Теорема.
Пусть
– 1.
–
2.
–
3.
–
4.
–
5.
x (t ),
y (t ), t t1 , t 2 ;
(t ) непрерывная ,
монотонная на t1 , t2 ;
(t0 ) , t0 t1 , t2 ,
(t0 ) 0 ;
(t ) непрерывная
на t1 , t2 ;
(t0 )
В т очке x0 (to )
(t0 )
y ( x0 )
(t0 )
14. Производная функции (17)
Производные высших порядков.
Определение 1.
Производная y f (x)
называется производной
первого порядка функции y
Определение 2.
Производная от производной первого порядка
называется производной второго порядка
функции
Определение 3.
Производная от производной (n-1) -порядка
y ( n ) a x (ln a) n
называется производной
функции
f (x)
y f ( x) : y ( f ( x))
n – порядка
y f ( x) : y(n) ( f (n 1) ( x))
Пример.
y ax
y a x ln a ;
y a x (ln a) 2 ;
15. Производная функции (4)
Связь между существованием производной
и непрерывностью функции.
–
Теорема.
f ( x) f ( x) непрерывнав т. x
–
Доказательство.
f ( x)
x 0 x
f ( x) lim
f ( x )
f ( x) ( x)
x
где 0 при х 0
f ( x) f ( x) x ( x) x
f ( x) 0 при x 0
f ( x) непрерывна в т. х
16.
• Связь между существованием производной• Замечание. Обратное утверждение теоремы
неверно, т.е. из непрерывности функции y f (x)
в точке x0 не следует существование производной
функции y f (x) в этой точке.
Пример.
x 0
x,
f ( x) x
.
x, x 0
Эта функция непрерывна в точке x 0, но в этой
точке функция не имеет производной.
17.
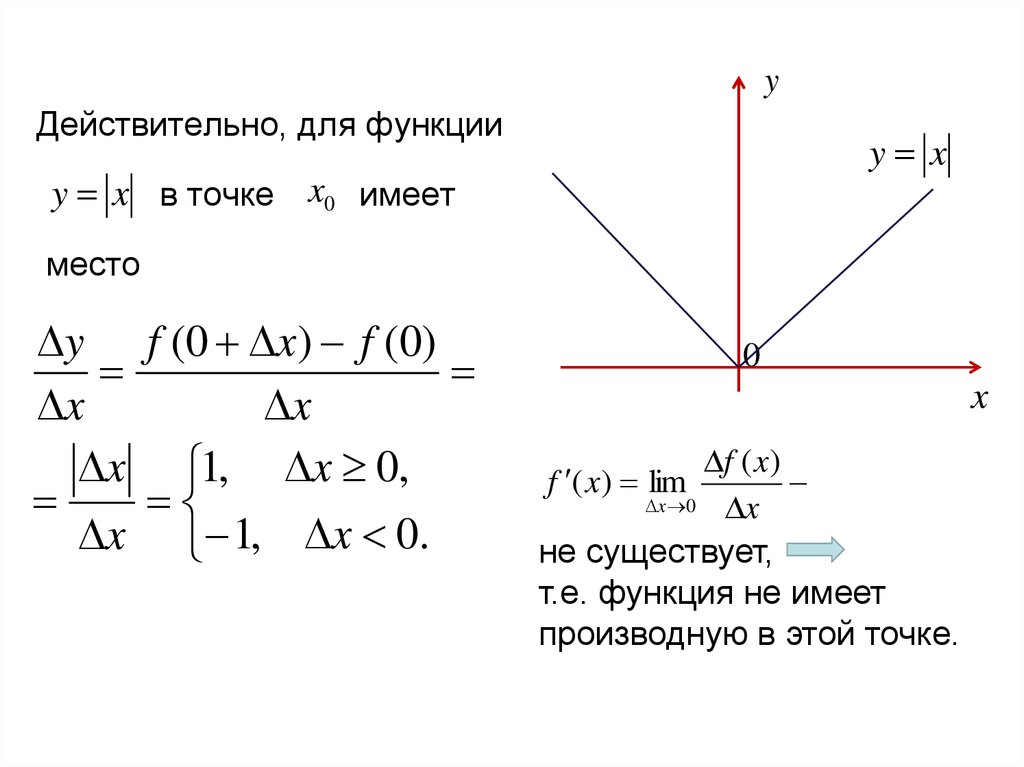
yДействительно, для функции
y x
y x в точке x0 имеет
место
y f (0 x) f (0)
x
x
x 1, x 0,
x 1, x 0.
0
x
f ( x)
f ( x) lim
x 0 x
не существует,
т.е. функция не имеет
производную в этой точке.









 Математика
Математика








