Похожие презентации:
О соотношениях понятий грубость, хрупкость и робастность в современной теории автоматического управления
1. Да здравствует, да пусть, ради Бога, и процветает наука об УПРАВЛЕНИИ !
О СООТНОШЕНИЯХ ПОНЯТИЙГРУБОСТЬ, ХРУПКОСТЬ И РОБАСТНОСТЬ
В СОВРЕМЕННОЙ
ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
2.
«… оптимальность становится опасной,если её принимать всерьёз»
Tukey J.W. The future of data analysis. –
-Ann. Math. Stat. No. 1, 1962.
И.П. Симаков
Доклад - лекция
на тему
СООТНОШЕНИЕ ПОНЯТИЙ ГРУБОСТЬ, ХРУПКОСТЬ
И РОБАСТНОСТЬ В СОВРЕМЕННОЙ
ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Санкт-Петербург
2015
3. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Грубость (нехрупкость) – свойство системы сохранять качественныехарактеристики поведения (прежде всего устойчивость!) при сколь
угодно малых вариациях параметров, что в линейном случае
обеспечивается сохранением устойчивости, а также при сколь угодно
малых вариациях операторов системы (изменении порядка СДУ).
Робастность – свойство системы сохранять устойчивость и некоторые
гарантированные характеристики поведения при вариациях
параметров и/или операторов системы в некоторых пределах.
Необходимым условием робастности является «грубость» !!!!.
Отказоустойчивость (живучесть) – свойство сохранять
работоспособность при разрывах в системе отдельных связей, при
отказах и отключениях оборудования и т.д.
4. Понятие ГРУБОСТИ по Андронову – Понтрягину «Грубые» системы сохраняют устойчивость при малых изменениях как параметров, так и
вида (порядка) дифференцильных равнений.Только «грубые» могут быть теоретическими моделями реальных
физических систем !!!
«... чтобы стационарные состояния могли длительное время
существовать в реальной системе, они должны быть
устойчивыми не только по отношению к малым изменениям
координат и скоростей (то есть к начальным условиям), но и
по отношению к малым изменениям самого вида
дифференциальных уравнений, описывающих систему. К
малым изменениям, которые не только не изменяют порядка
(числа) дифференциальных уравнений, но и повышают число
степеней свободы. Это всегда имеет место из-за наличия
«паразитных» параметров. При этом коэффициенты при
появившихся вновь более высоких производных достаточно
малы. Но мы не можем быть «наивными». А это значит, что
мы должны проверить, не нарушают ли устойчивости
данного состояния всевозможные малые паразитные
параметры,
повышающие
порядоксистемы
дифференциальных уравнений, описывающих систему. ... Но
окончательный ответ на вопрос об устойчивости того или
иного состояния в реальной системе может дать только
опыт.»
(см. кн. А.А. Андронов, А.А. Витт, С.В. Хайкин «Теория колебаний» - М.:
«Наука», 1981. с.33-37)
5. Предыстория вскрытия явления негрубости (хрупкости) систем с «оптимальными» регуляторами
Первоисточники1. Янушевский Р.Т. О грубости решения задачи аналитического конструирования
регуляторов // Автоматика и телемеханика, № 3, 1966. (критика лётовских
регуляторов).
2. Надеждин П.В. О практической неустойчивости (негрубости систем,
синтезированных по методу [1]. Автоматика и телемеханика, №5, 1973. (критика
методов Ларина и Сунцева).
3. Симаков И.П. О некорректности решения некоторых задач аналитического
конструирования оптимальных регуляторов и систем стабилизации параметров
движения судов» - В cб. «Проблемы создания систем управления судовыми
техническими средствами». – Л.: Изд-во «Судостроение», 1973 (критика Петрова
Ю.П.)
4. Симаков И.П. в Автоматика и телемеханика, № 4, 1974 (критика Ш. Чанга и др.).
5. Keel «Robust» (критика Н….…)
6. Afalaby }Catastro….
6. О проникновении англоязычных терминов в их прямом звучании в отечественную литературу по ТАУ
Англоязычный термин «робастность» в его прямомзвучании («robust» — дословно «крепкий», но, заметим,
не «грубый» в смысле Андронова) введен в
русскоязычную литературу
по ТАУ Я. 3. Цыпкиным и Б.Т. Поляком в 1990 г.
( Частотные критерии робастной устойчивости и апериодичности
линейных систем. – Автоматика и телемеханика, №9, 1990)
Этот термин используется в настоящее время в столь
широком смысле (в отличие от его первоначального
смысла и понимания), что охватывает не только вопросы
устойчивости
и
качества,
так
называемых,
параметрически неопределенных стационарных систем,
но и вопросы потери устойчивости при бесконечно малых
вариациях параметров и вида дифференциальых
уравнений.
7. Классификация «простейших» случаев неопределенности по видам характеристических полиномов Интервальность параметров q системы
приводит к различным видамнеопределенности ее характеристического полинома - его коэффициенты могут
являться либо интервалами, либо функциями интервалов q.
Интервальная неопределенность – коэффициенты полинома
являются интервальными параметрами
Аффинная неопределенность – коэффициенты полинома
образованы суммой или разностью интервальных параметров
Полилинейная неопределенность – коэффициенты полинома
линейно зависят от каждого параметра, если остальные параметры
фиксированы
Полиномиальная неопределенность – коэффициенты полинома
зависят полиномиально хотя бы от одного параметра
Для интервальной и аффинной неопределенностей существуют достаточно простые
методы анализа и синтеза, но если коэффициенты полинома являются более сложными
функциями интервальных параметров, то анализ и синтез ИС значительно
усложняется
И наконец!!!
Параметрические возмущения - коэффициенты» полинома и/или
интервальные параметры – произвольные заранее неизвестные
функции времени – и мы приходим к НОВЫМ ТИПАМ ОБРАТНОЙ
СВЯЗИ !!!
8. Уточнение смысла и установление взаимосвязи между широко используемыми понятиями в современной литературе по ТАУ, которые часто
и некорректноподменяют друг друга.
- «грубость» динамической системы, введенное в 1937 г. советскими
учеными А.А. Андроновым и Л.С. Понтрягиным (Грубые системы. ДАН СССР, 1937, т. 14, № 5). В англоязычной литературе – «Coarse
systems»
- «robustness» динамической системы (буквальный перевод –
«крепкая», «здоровая» система), введенное в 1980 г. американским
ученым М.Г. Сафоновым (M.G. Safonov.
Stability and robustness of
multivariable feedback systems. - Cambridge, MA: MIT Press, 1980).
- «fragility» динамической системы (буквальный перевод – «хрупкая»
система), введенное в 1997 г. американскими учеными L.H. Keel, S.R.
Bhattacharyya (статья «Robust, fragile or optimal?» – IEEE – Trans. Autom.
Control, 1997, 42.(Proceedings of the American Control Conferense. Meixco, June
1997), D. Afolabi. (Optimal Controllers are Fragile. – IET Control Theory Appl. Vol.
1,
No.
5,
September
2007.),
появившееся при обнаружении
неработоспособности систем (потери устойчивости системы при малых
вариациях
параметров)
с
оптимальными
регуляторами,
синтезированными методами H∞ - теории оптимизации
9. О проблеме робастности
Проблема робасности в широком понимании заключается визучении вопроса о сохранении определенных свойств
динамической системы при возможных вариациях некоторых
ее характеристик или условий функционирования.
Для решению задач обеспечения робастности систем
управления предложены, в частности, три пакета
прикладных программ (ППП) системы Matlab, входящие в
группу “Оптимальные и робастные системы управления”:
Robust Control,
µ-Analysis and Synthesis,
LMI Control).
10. О возникновении теории робастных систем
Основополагающей работой, определившей возникновениетеории робастности, является
теорема В.А. Харитонова,
впервые сформулированная в его статье
«Асимптотическая устойчивость положения равновесия
семейства систем дифференциальных уравнений»
Дифференциальные уравнения. — 1978. — № 11. — С. 2086–2088.
Достаточные условия робастности интервальных полиномов
получены в 1953 г. Фаедо
Получено блестящее решение!
Но для частного и наиболее простого случая
неопределенности – постоянные во времени интервально
заданные, но независимые друг от друга значения
коэффициентов характеристического уравнения.
11. Некоторые подходы
Первый подход Robust Control связан с именами M. Safonov, M. Athansи базируется на введенном в работе
Safonov M. G., Athans M. A multiloop generalization of the circle criterion for
stability margin analysis // IEEE Trans. on Automatic Control. — 1981. —
Vol. 26, no. 2. — P. 415–422. понятии многомерной границы
устойчивости (MSM).
Второго подхода µ-Analysis and Synthesis предложен в работе Doyle J. C.
Analysis of feedback systems with structured uncertainties // IEE Proc.
Pt. D: Control theory and applications. — 1982. — Vol. 129, no. 6. — P. 242–
250. и основан на концепции структурированного сингулярного
числа μ.
Третий подход связан с применением линейных матричных
неравенств в теории управления – подробное рассмотрение вопроса и
библиография даны в работе Boyd S., Ghaoui E., Feron E., Balakrishnan
V. Linear matrix inequalities in systems and control theory. — Philadelphia:
Society for Industrial and Applied Mathematics, 1994. — ix, 193 p.
12. О проблеме робастности
Проблема робастности в широком понимании заключается визучении вопроса о сохранении определенных свойств
динамической системы при возможных вариациях некоторых
ее характеристик или условий функционирования.
Для решению задач обеспечения робастности систем
управления предложены, в частности, три пакета
прикладных программ (ППП) системы Matlab, входящие в
группу “Оптимальные и робастные системы управления”:
Robust Control,
µ-Analysis and Synthesis,
LMI Control).
13. О программной реализации методов синтеза робастных систем в ПК «МатЛаб»
Первый подход Robust Control связан с именами M. Safonov, M. Athans ибазируется на введенном в работе
Safonov M. G., Athans M. A multiloop generalization of the circle criterion for
stability margin analysis // IEEE Trans. on Automatic Control. — 1981. —
Vol. 26, no. 2. — P. 415–422. понятии многомерной границы
устойчивости (MSM).
Второго подхода µ-Analysis and Synthesis предложен в работе Doyle J. C.
Analysis of feedback systems with structured uncertainties // IEE Proc. Pt. D:
Control theory and applications. — 1982. — Vol. 129, no. 6. — P. 242–250. и
основан на концепции структурированного сингулярного числа μ.
Третий подход связан с применением линейных матричных
неравенств в теории управления – подробное рассмотрение вопроса и
библиография даны в работеBoyd S., Ghaoui E., Feron E., Balakrishnan V.
Linear matrix inequalities in systems and control theory. — Philadelphia:
Society for Industrial and Applied Mathematics, 1994. — ix, 193 p.
14.
Критерий «грубости» - сохранения устойчивости к сингулярным возмущениям15. Работы американских об обнаружении неработоспособности («хрупкости») систем с «оптимальными» регуляторами, синтезированными
строгими методами H∞- оптимизацииОсновные публикации
L.H. Keel, S.R. Bhattacharyya.
Robust, fragile or optimal? – IEEE –
Trans. Autom. Control, 1997, 42.
D. Afolabi.
Optimal Controllers are Fragile. –
IET Control Theory Appl. Vol. 1, No. 5,
September 2007.
D. Afolabi.
Catastrophes in Control Systems. –
Darsaki Publications, Inc, Indiana,
USA.
16. К Понятиям хрупкости и робастности
Хрупкость(варьируются только коэффициенты
регулятора!)
Может трактоваться как
необходимое условие
робастности
Было показано, что
некоторые «робастные»
системы являются
хрупкими
Робастность
Относится к интервальным
системам или системами с
неопределенными
параметрами
17. Хрупкость (fragile) оптимальных H2,H∞ систем
В теории H2,H∞ естьпримеры синтезированных
оптимальных, но …
«хрупких» регуляторов;
Изменение параметров
регулятора на 10-5%
приводит к потере
устойчивости системы;
18. In this paper we show by examples that optimum and robust controllers designed by using the H2, Hinf, I’ and p formulations,
Proceedings of the American Control ConferenceAlbuquerque, New Meixco June 1997
ROBUST, FRAGILE OR OPTIMAL?
L.H. Keel, S .P. Bhattacharyya
Department of Electrical Engineering
Texas A&M University
Center of Excellence in Information Systems
Tennessee State University
In this paper we show by examples that optimum and robust controllers designed by using the H2,
Hinf, I’ and p formulations, can produce extremely fragile controllers,In the sense that vanishingly
small perturbations of the coefficients of the designed controller destabilize the closed loop control
system. The examples show that this fragility also usually manifests itself as extremely poor gain and
phase margins of the closed loop system.
19. Optimal controllers are structurally unstable. The instability is intrinsic because of constrained optimization. This kind of
Proceedings of the American Control ConferenceDenver. Colorado June 4-6.2003
Optimal Controllers are Fragile
Dare Afolabi
Department of Mechanical Engineering
Indiana University Purdue University Indianapolis
Optimal controllers are structurally unstable. The instability
is intrinsic because of constrained optimization. This kind of
instability is sometimes identified with “fragility” in the control
literature. The fragility is related to hidden degeneracies
in the polynomials and matrices of the optimized systems,
and may detected by looking for certain catastrophe fingerprints
20. Примеры хрупких регуляторов, синтезированные методами теории Н∞-оптимизации
С использованием теории Н∞-оптимизации для объектасинтезирован регулятор
s 1
P( s) 2
s s 2
379s 6 39383s5 192306s 4 382993s3 383284s 2 192175s 38582
C
3s 6 328s5 38048s 4 179760s3 314330s 2 239911s 67626
обеспечивающий верхнюю границу запаса устойчивости на максимальном
значении.
При этом полюса замкнутой системы
таковы:
0.4666 i 14.2299;
5.5334 i 11.3290;
1.0002;
1.0000 i 0.0002;
0.9998.
21.
Keel в своей статье показал,что такая система теряет устойчивость при малейших изменениях
параметров регулятора, .
И назвал её ХРУПКОЙ
Так, при измении параметров синтезированного
регулятора всего на 0.001%
379.0003s 6 39382.9997 s5 192305.9999 s 4 382993.0005s3 383284.0007s 2 192174.9999s 38582
C
,
6
5
4
3
2
3.0008s 327.9998s 38048.0008s 179760.0002 s 314329.9999s 239910.9999s 67626.0002
полюса замкнутой системы таковы:
98.8920;
2.4622 i 1.9267;
1.2750 i 0.8824;
1.0000;
0.6545.
То-есть, замкнутая система становится неустойчивой.
Такой регулятор назван ХРУПКИМ
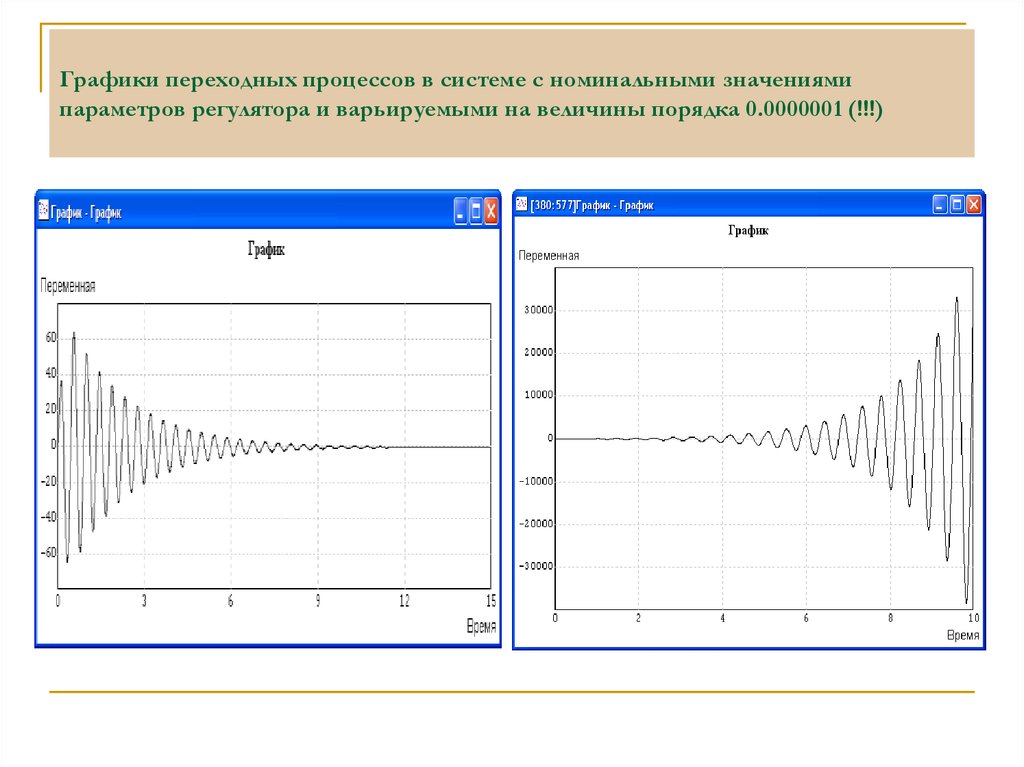
22. Графики переходных процессов в системе с номинальными значениями параметров регулятора и варьируемыми на величины порядка
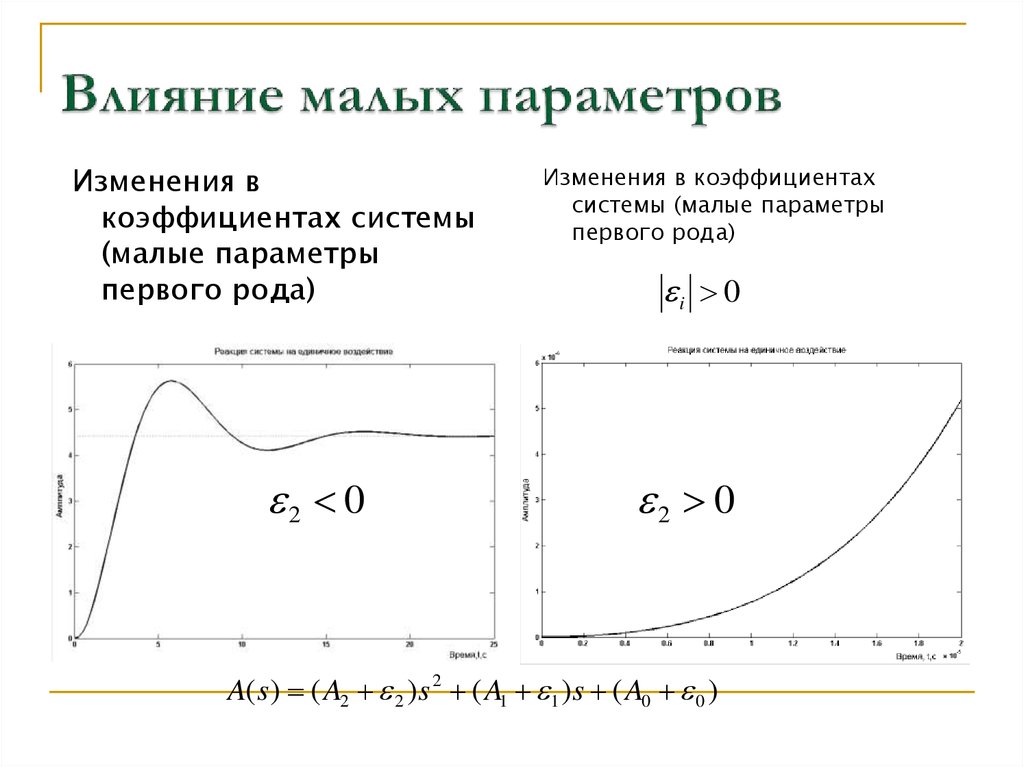
0.0000001 (!!!)23. Влияние малых параметров
Изменения вкоэффициентах системы
(малые параметры
первого рода)
2 0
Изменения в коэффициентах
системы (малые параметры
первого рода)
i 0
2 0
A( s) ( A2 2 ) s 2 ( A1 1 ) s ( A0 0 )
24. Влияние малых параметров
Сингулярные возмущения (малыепараметры второго рода)
1
, 0
s 1
25.
О задачах синтеза статистически оптимальныхсистем
Ax u f
A – гурвицев полином
u - управление
f – случайное возмущение с определенной
спектральной плотностью
Для таких систем необходимо разработать регулятор, который бы
минимизировал сумму дисперсий x и u
T
J lim ( x u )dt
2
T
0
2
2
26.
«Классические» методы синтеза(Чанг, Ларин – Сунцев, Катковник – Полуэктов,
Ю.Петров и др.
Для спектральной плотности
S
4 ( 2 2 )
Df
2
2
[ jw 2 ][ jw 2 ]
Оптимальным является регулятор
Y ( s)
u A( s )
k0 k1s
здесь
Y ( s)Y ( s) 1 2 A( s) A( s)
Оптимальная замкнутая система:
k0 k1s
F ( s)
Y ( s)
27. Постановка задачи оптимальной стабилизации угла крена
Уравнение объектаJ x M x x u f (t )
или
T12 T2 u f (t )
Корреляционная _ функция
K f ( ) D f e (cos
sin )
Спектральная _ плотность
2 2
S f ( ) D f
( 2 2 2 ) 2 4 2 2
4
Критерий
T
J lim (m 2 2 u 2 )dt m 2 2 u 2
T
0
28. Численные параметры и характеристики
Т 12 4.01с 2 ; T2 0.2c; (Tсобств _ колеб 12.5с)m 1; 1; 0.21;
2
A( p) 4.01 p 0.2 p 1;
2
B( p) 4.01 p 2 1.83 p 1.41;
A( j )
K1 jK 2
0.745 0.362 j
Y ( j )
a 669; b 0.362(b 0!)
29. «Оптимальный» регулятор
Уравнения2
4
.
01
p
1.825 p 1.414
2
u [4.01 p 0.2 p 1
]
0.669 0.362 p
(4.01 p 2 1.83 p 1.414) (0.669 0.362 p) f ;
(4.01 p 1.83 p 1.414) ( 1.445 p 1.3 p 1.6 p 2.08) f .
2
3
2
Корни _ чарактеристического _ уравнения :
p1 0.228 0.56 j; p2 0.228 0.56 j.
0.145; u 0.262(приD f 1).
2
2
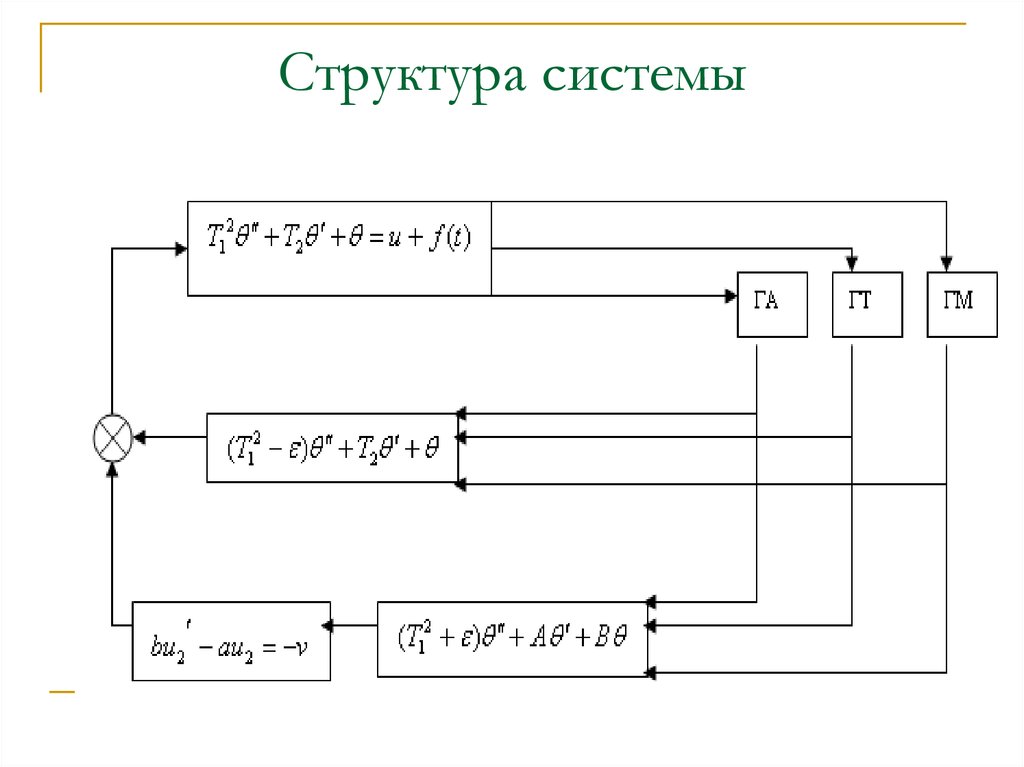
30. Структура системы
31.
A 2 * ( 1 m 2 1) T22 ;B 1 m2 ;
неустойчивое _ звено
Характеристическое уравнение замкнутой системы
Т 12 p 2 Ap Bp 0
bp
3
T12
[(
a 1) s 2 Ps N ] 0
Jx
T1 2
и b T1 s и (aT1 b T2 ) s и (aT2 b ) s ( s Ps N ) 0
4
3
2
32.
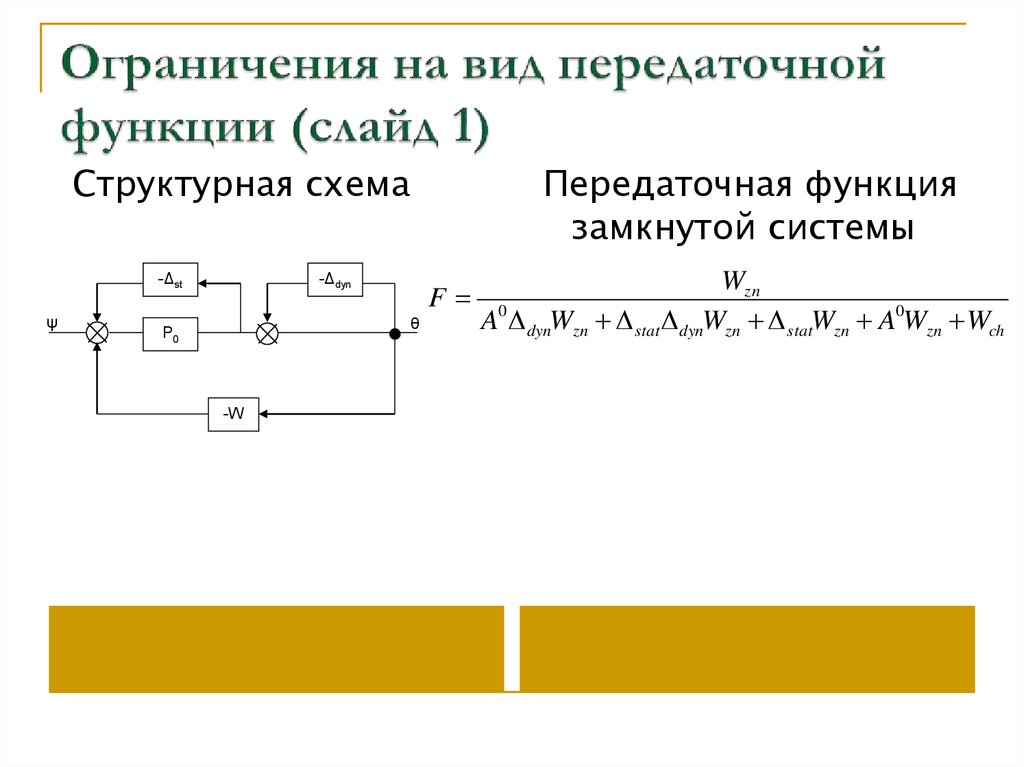
Структурная схема-Δst
ψ
Передаточная функция
замкнутой системы
-Δdyn
θ
P0
-W
Wzn
F 0
A dynWzn stat dynWzn statWzn A0Wzn Wch
33. Ограничения на вид передаточной функции
Малые параметрыпервого рода
Малые параметры
второго рода
deg( A0Wzn Wch ) deg( A0Wzn )
Знак коэффициентов
A Wzn Wch
должен совпадать со знаком
0
коэффициентов A Wzn Wch
0
гурвицев
Wzn
34. Проверка классических регуляторов на ограничения
Классические регуляторы (Чанг, Петров) неудовлетворяют указанным ограничениям
deg( A0Wzn Wch ) deg( A0Wzn )
не выполняется
deg( Fzn ) deg( A Fch )
0
Знак коэфф-ов
Wzn
k0 k1s
F ( s)
Y ( s)
должен совпадать со знаком коэфф-ов
k0 k1s
F ( s)
Y ( s)
A0Wzn Wch
не выполняется
35. Попытка синтеза регулятора с учетом указанных ограничений
(4.01s 2 0.2s 1) x u f4 0.21 1.0441
S ff 2
( s 0.42s 1.0441)( s 2 0.42s 1.0441)
Оптимальная система
Малые параметры
первого рода
0.3396s 6.26684
F ( s)
4.01( s 2 0.4572s 0.3527)(1 0.001s)
Малые параметры
второго рода
W ( s) k1 k 2 s k3 s
2
6.26684
F ( s)
4.01( s 2 0.4572s 0.3527)
36. Негрубость летовских регуляторов
Рассмотрим объект с передаточной функцией1
Woá 3
p 0.5 p 2 0.72 p 0.1
Для данной модели
управление ,
методом аналитического конструирования найдено
u ( s) (20s 2 22s 16.7) x1 ( s)
которое минимизирует функционал
J ( x12 0.003u 2 )dt
0
Передаточную функцию регулятора, реализующее управление, близкое
к оптимальному, можно представить следующим образом
20 p 2 22 p 16.7
Wðåã ( p)
, ãäå m 0
2
1 m(20 p 22 p 16.7)
37. График переходного процесса при m=0.000000001
38. Хрупкость μ-оптимальных систем
Запас устойчивости неявляется прямым
показателем
хрупкости
оптимальных систем;
Критерии качества
могут быть
произвольными.
39. ВЫВОДЫ
методы синтеза оптимальных систем стабилизации при случайныхвозмущениях [1-8] не учитывают влияния на устойчивость
неточностей реализации в регуляторе расчетных соотношений, а
также влияния малых динамических параметров и приводят в общем
случае к негрубым или практически неустойчивым системам.
При использовании идей оптимальной фильтрации ВинераКолмогорова к синтезу систем с обратной связью кроме требований
не компенсации правых нулей передаточной функции объекта
необходимо с целью обеспечения грубости в более широком смысле
накладывать дополнительные требования к структуре передаточной
функции замкнутой системы.
В связи с этим уместно подчеркнуть связь характеристик случайных
возмущений, принимаемых при расчете оптимальной системы, со
свойством ее грубости. Так, принимая при расчете оптимальной
системы стабилизации крена судна корреляционную функцию
морского волнения в виде и используя методы [1-8], получаем
оптимальную систему, обладающую свойствами грубости.
40. Выводы
Теориясинтеза оптимальных регуляторов нуждается в
развитии, так как существующие методы приводят к негрубым в
смысле Андронова – Понтрягина системам. Термин «хрупкость»
полностью эквивалентен термину «негрубость» и не должен
вносить путаницу в отечественную литературу.
Англоязычный
термин «робастность» заменить теперь, повидимому, не удастся, так как в РАН имеются даже лаборатории
«Робастных систем» . Рациональнее всего использовать этот
термин только для параметрически неопределенных систем,
например интервальных.
Грубость
следует считать необходимым условием робастности.
41.
«… оптимальность становится опасной,если её принимать всерьёз»
Tukey J.W. The future of data analysis. –
Ann. Math. Stat. No. 1, 1962.
42.
РАЗВИТИЕ и ОБОБЩЕНИЕпонятий УСТОЙЧИВОСТИ И УСТОЙЧИВОСПОСОБНОСТИ
43.
«…тщательный анализ аварийныхсобытий свидетельствует о том, что
центр тяжести проблем лежит все-таки в
области управления, где человеческий
фактор наиболее существен.
Выясняется, что сами инструкции были
либо не очень точны и не
предусматривали, а в некоторых случаях
и не могли предусмотреть правил
поведения при возникновении
нештатных режимов».
Академик Легасов Валерий Алексеевич
-журнал «Коммунист» № 8 за 1987 г.,
- статья «Проблемы безопасного развития техносферы»,
- с. 92 – 101.
44. О состоянии терии управления
«Теория управления, каки самая красивая
девушка Парижа, не
может дать больше того,
чем она располагает»
Марк Аронович Айзерман
45.
4546.
ОСНОВОПОЛОЖНИКИ:ТРАПЕЗНИКОВ Вадим Александрович
ДЕМЧЕНКО Олег Павлович
ВОЛИК Борис Григорьевич
СИСТЕМА КРИТЕРИЕВ
ВЫБОРА СТРУКТУРНОЙ ОРГАНИЗАЦИИ УПРАВЛЯЮЩИХ СИСТЕМ
типа СУ ТС кораблей и АСУ ТП
и ОПРЕДЕЛЯЮЩИХ АППАРАТНО-ПРОГРАММНЫХ ТЕХНИЧЕСКИХ
РЕШЕНИЙ
А. ДЕТЕРМИНИРОВАННЫЕ КРИТЕРИИ СТРУКТУРНОЙ
УСТОЙЧИВОСТИ
А.1. КРИТЕРИИ абсолютной (!) ОТКАЗОБЕЗОПАСНОСТИ
и отказоустойчивости УС при любых одиночных нарушениях с
учётом накопления "скрытых" отказов (без ограничений на
ресурсы !)
А.2. КРИТЕРИИ ЖИВУЧЕСТИ УС при частичных повреждениях
для любого аварийного воздействия внешней среды из априори
установленного множества взаимоисключающих гипотез
46
47. СИСТЕМА КРИТЕРИЕВ ВЫБОРА СТРУКТУРНОЙ ОРГАНИЗАЦИИ ИУС типа СУ ФКТС кораблей и АСУ ТП и ОПРЕДЕЛЯЮЩИХ АППАРАТНО-ПРОГРАММНЫХ
ТЕХНИЧЕСКИХ РЕШЕНИЙА. ДЕТЕРМИНИРОВАННЫЕ КРИТЕРИИ СТРУКТУРНОЙ УСТОЙЧИВОСТИ
А.1. КРИТЕРИИ абсолютной (!)ОТКАЗОБЕЗОПАСНОСТИ
отказоустойчивости) УС при любых одиночных нарушениях с учётом
накопления "скрытых" отказов (без ограничений на ресурсы !)
А.2. КРИТЕРИИ ЖИВУЧЕСТИ УС при частичных повреждениях для любого
аварийного воздействия внешней среды из априори установленного
множества взаимоисключающих гипотез
Б. КРИТЕРИИ типа "ЭФФЕКТИВНОСТЬ - ЗАТРАТЫ"
С вероятностными показателями функциональной эффективности, системной
надежности УС (как многофункциональной системы), риска нарушения
условий безопасности (технической, ядерной, радиационной,
экологической), потерь от ненадёжности, общих затрат различных видов) с
выбором предпочтительных (Парето- оптимальных) решений
В. КРИТЕРИИ МНОГОУРОВНЕВОЙ и РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
между системами 2-х соподчиненных рангов
Г. КРИТЕРИИ ПРОИЗВОДСТВЕННЫЕ типа "ВРЕМЯ СОЗДАНИЯ - ЗАТРАТЫ
ЖИВОГО ТРУДА"
Д. КРИТЕРИИ ГОСУДАРСТВЕННЫЕ:
интересы государства, занятость ИТР и производственного персонала,
научно-техническая политика.
47
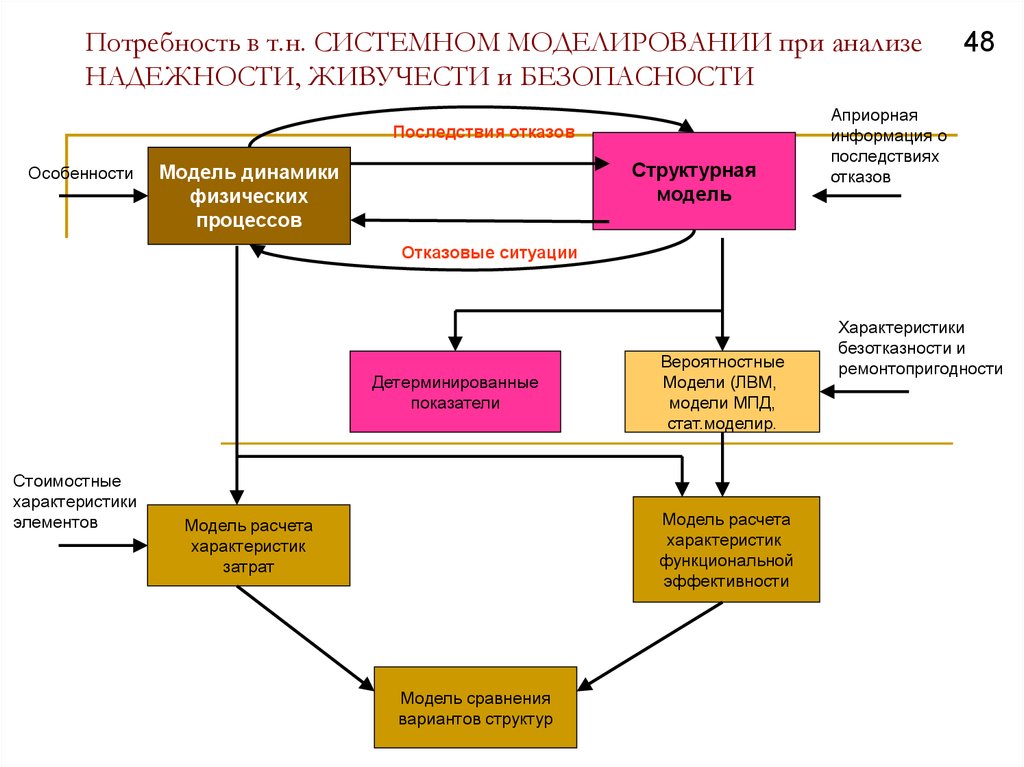
48. Потребность в т.н. СИСТЕМНОМ МОДЕЛИРОВАНИИ при анализе НАДЕЖНОСТИ, ЖИВУЧЕСТИ и БЕЗОПАСНОСТИ
Последствия отказовОсобенности
Структурная
модель
Модель динамики
физических
процессов
48
Априорная
информация о
последствиях
отказов
Отказовые ситуации
Детерминированные
показатели
Стоимостные
характеристики
элементов
Вероятностные
Модели (ЛВМ,
модели МПД,
стат.моделир.
Модель расчета
характеристик
функциональной
эффективности
Модель расчета
характеристик
затрат
Модель сравнения
вариантов структур
Характеристики
безотказности и
ремонтопригодности
49.
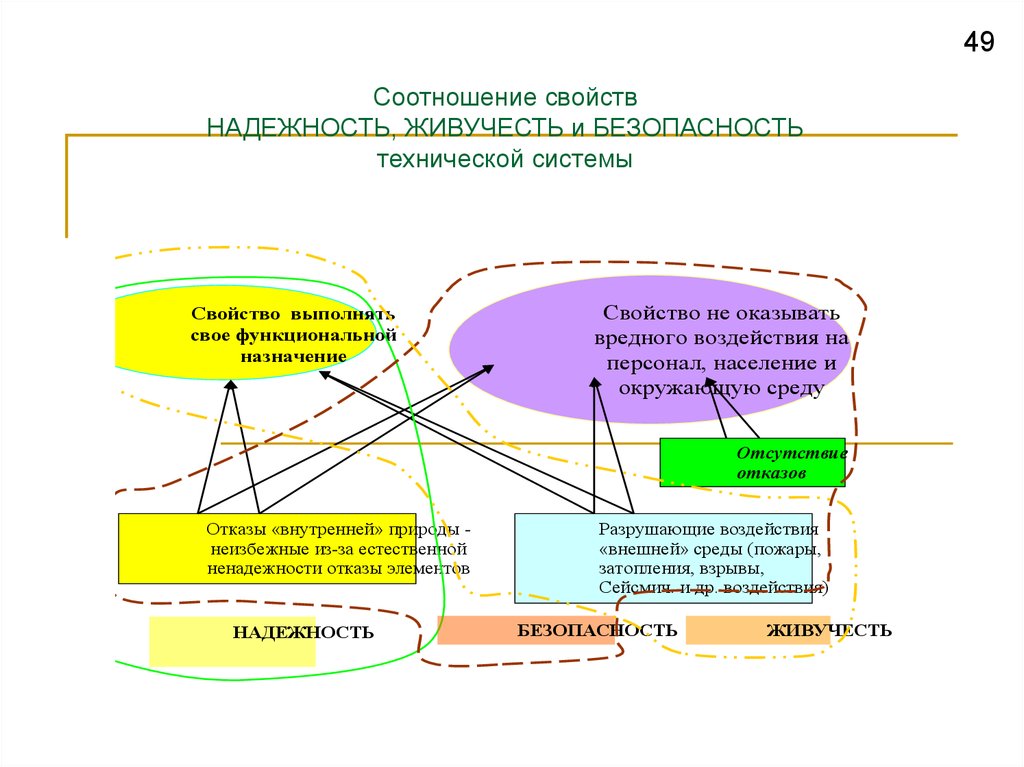
49Соотношение свойств
НАДЕЖНОСТЬ, ЖИВУЧЕСТЬ и БЕЗОПАСНОСТЬ
технической системы
Свойство выполнять
свое функциональной
назначение
Свойство не оказывать
вредного воздействия на
персонал, население и
окружающую среду
Отсутствие
отказов
Отказы «внутренней» природы неизбежные из-за естественной
ненадежности отказы элементов
НАДЕЖНОСТЬ
Разрушающие воздействия
«внешней» среды (пожары,
затопления, взрывы,
Сейсмич. и др. воздействия)
БЕЗОПАСНОСТЬ
ЖИВУЧЕСТЬ
50. Пример 2.
Задан ОУ: P( s)H регулятора Doyle
( s 1)
2
( s 1)( s С0(.5s)) ( s 1)(124.5s 240.45s 120)
s 3 227.1s 2 440.71s 220
Синтезирован регулятор:
Собственные числа замкнутой системы: 0.99996 i 0.00006
1.00007
0.09999
99.9999
Вывод: не всегда синтезированные
H - регуляторы
при малом изменении в параметрах, становятся хрупкими
( не работоспособными).












































 Программное обеспечение
Программное обеспечение








