Математическая статистика

1.

2. Математическая статистика

Темой сегодняшнего урока будет математическая статистика. Как
видно из названия, предмет занимается статистикой, используя
различные методы математики. Математическая статистика, вполне себе
самостоятельно развивающийся раздел математики, в котором существуют и свои
уникальные способы решения и задачи.
Так чем же занимается и для чего нужна математическая
статистика.
Предположим, что у учеников девятых классов измерили рост. Что
делать с полученными данными?
Можно записать их в строчку друг за другом, можно разделить данные по классам,
можно попробовать создать таблицу. Но все эти способы довольно таки громоздкие и
неудобные, много информации из такого набора чисел будет извлечь довольно
таки сложно. А теперь представьте, что измерили рост учеников девятых классов всех
школ в одном городе. Количество измерений может перевалить далеко за тысячи, как же
удобно будет записать данные?
Так вот математическая статистика и занимается обработкой данных и
преобразованием их к виду более понятному для восприятия. Правда, это только одна
из задач статистики. Построение прогнозов, оценок, применимости различных
методов, достоверность проведенных испытаний и многое другое, то чем
занимается статистика.

3. Математическая статистика

Как же обрабатывают информацию?
1) Данные измерений упорядочивают и группируют.
2) Составляют таблицы распределений данных.
3) По таблицам строят графики распределений.
4) В итоге получается некоторый паспорт измерений, в
котором
собранно
небольшое
количество
числовых
характеристик полученной информации.
Давайте рассмотрим последовательно наши пункты.

4. Математическая статистика

1) Упорядочивание и группировка данных.
Первое что нам следует сделать при анализе данных,
определить рамки, в которых мы находимся.
Логически выбирается наименьшее и наибольшее допустимое
значение, они могут не совпадать с конкретными данными.
Например, при измерении роста учеников, шансов, что кто-то будет
ниже 140 сантиметров и выше 200 сантиметров очень мало, если найдется
такой вариант, то данные статистики всегда можно поменять.
При
измерении
роста
могут
получиться
числа:
140,150,160,170,180,190,200 – это общий ряд данных, данные принято
располагать в порядке возрастания.
Общий ряд данных может быть, и другим, например, такой:
140,145,150,155,160,…,190,195,200.
Как составить общий ряд данных зависит от конкретной
задачи.

5. Математическая статистика

Пример. Составить общий ряд данных:
а) Месяцев рождения одноклассников б) Годов рождения
родственников и друзей в) Букв с которых начинается слово.
Решение.
а) Всего 12 месяцев, если их перечислить по цифрам, то получим
общий ряд : 1,2,3,4,5,6,7,8,9,10,11,12.
б) Шансов того что кто то из родственников много старше 100 лет
очень мало, а вот, то, что кто то родился в этом году есть, тогда общий ряд годов
рождения мы можем составить таким образом:
1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
в) Слово может начинаться с любой буквы нашего алфавита кроме букв
ь,ы,ъ. Тогда у нас осталось 30 вариантов, если буквы записать численным
способом то получим:
1,2,3,4,…,28,29,30.
Понятие общий ряд не является строгим понятием, в примере
под буквой б) мы могли начать наш ряд и с 1900 года, ряд бы так же
остался общим.

6. Математическая статистика

При проведении эксперимента, многие данные из общего
ряда могут не встречаться.
Вернемся к нашему примеру под буквой б и рассмотрим конкретный
случай.
Вова назвал вот такие года рождения родственников:
1935,1937,1960,1965,1980,1981,1997,2005.
Общий ряд у нас представлял собой:
1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
У Вовы встретились конкретные измерения которые
называются вариантой измерения.
Варианта измерения – один из возможных вариантов
проведенного измерения.
Если все варианты измерений перечислить по порядку то
получится ряд данных измерения.
Для нашего примера составим такую таблицу:

7. Математическая статистика

Пример.
Выписать ряд данных измерения, состоящий из букв слов: мама, папа,
брат, сестра, бабушка, дедушка, тетя, дядя.
Решение.
Ряд будет выглядеть вот так: а,б,д,е,к,м,п,р,с,т,у,ш,я. Получилось, что
встретились 13 букв из 33.
Некоторые буквы встречаются много раз, например буква а – девять раз.
Другие встречаются реже.
Определение. Если среди всех данных конкретного измерения одна
из вариант встретилась ровно к раз, то число к называют кратностью
измерения.
В
нашем
примере
у
буквы
а
кратность
равна
девяти.
Запишем кратности для каждой из букв:
абдекмпрстушя
9343222224223
Далее варианты нужно сгруппировать. Создадим сгруппированный ряд
данных:
а,а,а,а,а,а,а,а,а,б,б,б,д,д,д,д,е,е,е,к,к,м,м,п,п,р,р,с,с,т,т,т,т,у,у,ш,шя,я,я.
Число повторений каждой варианты равно кратности варианты.

8. Математическая статистика

Составление таблицы распределения данных.
Если сложить все кратности, то получится количество всех
данных измерения – объем измерения.
Объем измерения равен количеству букв встречающихся в наших
словах. Для проверки всегда складывают кратности, сумма должна
равняться количеству элементов измерения.
Далее вычисляют частоту варианты.

9. Математическая статистика

Составим таблицу частот измерений:
Сумма всех частот всегда равна единице, так как это сумма
всех дробей с одинаковым знаменателем, а сумма всех числителей как раз и
равна знаменателю.
Для удобства, часто переводят частоты в проценты от
объема измерения. Составим таблицу еще одну таблицу, каждую частоту в
новой строке помножим на 100.

10. Математическая статистика.

Графическое представление данных.
По нашим таблицам давайте построим графики функций
распределения.
Давайте только договоримся, что теперь вместо букв будем
использовать цифры 1,2,3,...,13. Тогда наша таблица примет вид:
По оси абсцисс отложим значения наших вариант, которые мы
договорились записать в виде цифр. А по оси ординат значения частот
появления вариант. Графическое изображение имеющейся информации –
график распределения частот.
Таблица значений:

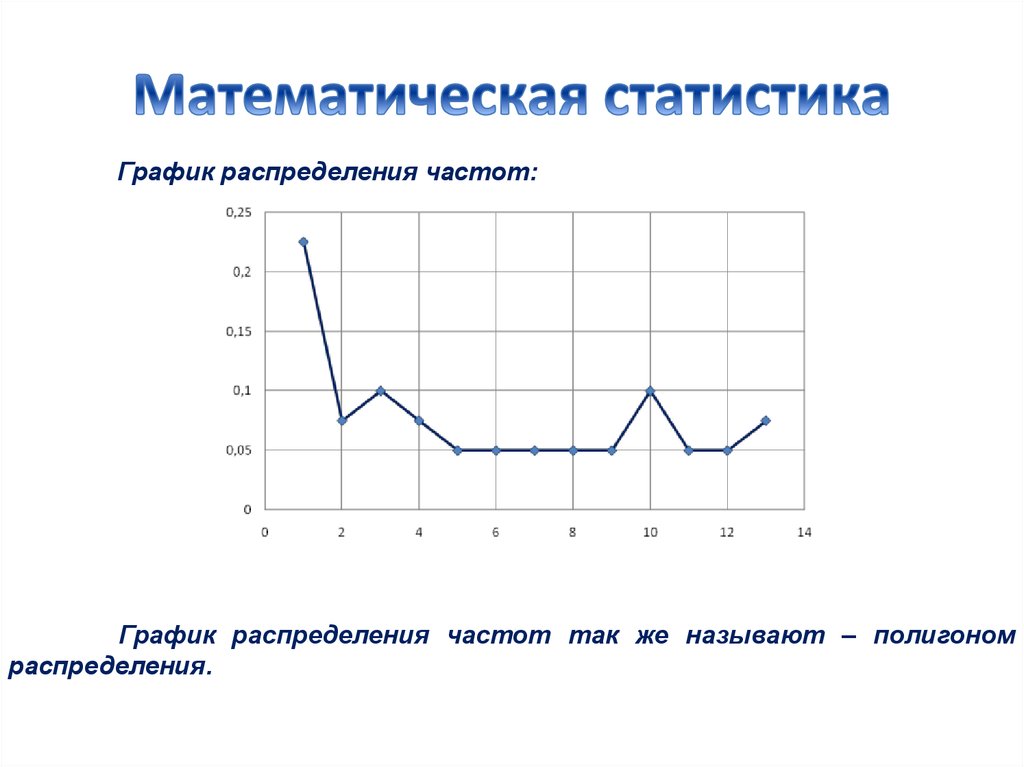
11. Математическая статистика

График распределения частот:
График распределения частот так же называют – полигоном
распределения.

12. Математическая статистика

Давайте так же построим график распределения частот
процентов. Его также называют полигоном распределения процентов.
Таблица значений.
Полигон распределения процентов:
Даже не большая по объему данных задача, представляет
собой довольно таки утомительную процедуру подсчета и составления
таблиц и графиков распределений.

13. Математическая статистика

Числовые характеристики данных измерения.
Наши
данные
обладают
своим
уникальными
числовыми
характеристиками.
Давайте определим некоторые из них:
Разность между максимальной и минимальной вариантой
называют размахом измерения.
На наших графиках это область определения, разность крайнего правого
значения на оси абсцисс и крайнего левого значения. В нашем примере размах
равен 13-1=12.
Варианта, которая встречается чаще других, называется модой.
В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем
наибольшее число, и смотрим, какой варианте оно соответствует. На графике, это
точка в которой достигается максимальное значение.

14. Математическая статистика

Наиболее важная характеристика – среднее значение (среднее
арифметическое или просто среднее)
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
Так же можно искать среднее значение таким способом:
а) Каждую варианту умножить на ее частоту
б) Сложить получившиеся значения.
Подсчитаем этим способом:

15. Математическая статистика

Давайте рассмотрим еще один пример.
На экзамене по математике 25 учеников 9 класса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
а) Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в
ряде – варианты измерений.
Составим сгруппированный ряд:
2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.

16. Математическая статистика

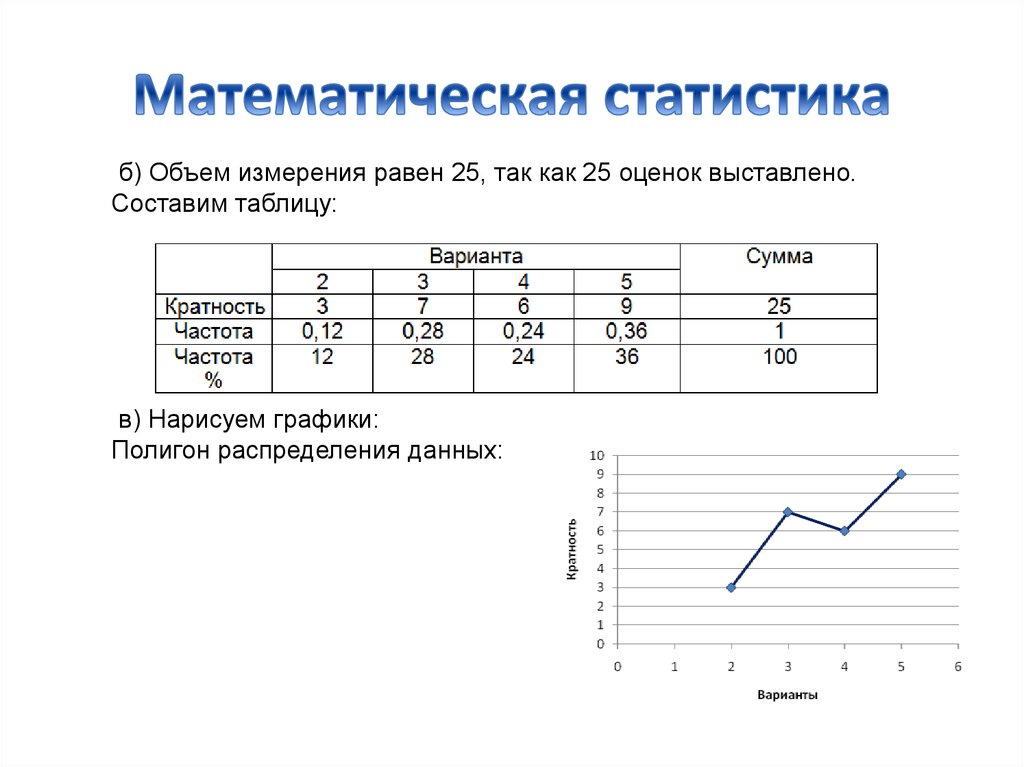
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:
в) Нарисуем графики:
Полигон распределения данных:

17. Математическая статистика

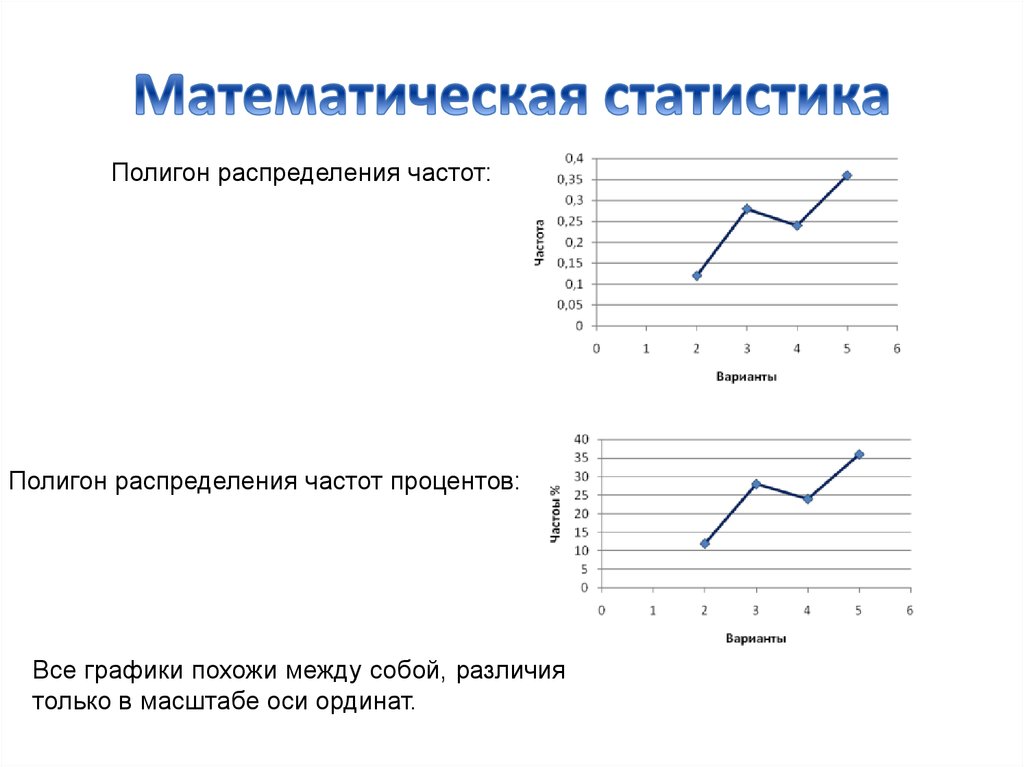
Полигон распределения частот:
Полигон распределения частот процентов:
Все графики похожи между собой, различия
только в масштабе оси ординат.

18. Математическая статистика

г)
Найдем среднее значение:
2·0,12+3·0,28+4·0,24+5·0,36=0,24+0,84+0,96+1,8=3,81.
Мода:
Чаще всего встречается оценка пять, она и будет модой.
Размах:
5-2=3.

19. Математическая статистика

.
Задачи для самостоятельного решения.
На экзамене по математике 50 учеников 9 класса получили такие оценки:
5,3,4,4,5,4,3,2,4,3,5,1,2,3,5,4,5,3,3,4,5,5,4,3,1,3,4,5,4,3,2,2,1,4,4,5,5,4,4,5,3,3,3,2,1,5,4,
3,2,5.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.